8.1基本立体图形 课件(共46张ppt)2023-2024学年高中数学人教A版(2019)必修第二册
文档属性
| 名称 | 8.1基本立体图形 课件(共46张ppt)2023-2024学年高中数学人教A版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 00:00:00 | ||
图片预览









文档简介
(共46张PPT)
人教版必修第二册A版
8.1《 基本立体图形 》
( 3 课 时 )
教学目标
学习目标:1.利用实物,认识与理解空间几何体、简单几何体的概念与分类.(直观想象)
2.理解与掌握棱柱、棱锥、棱台、圆柱、圆锥、圆台、球的定义及其结构特征,并能应用其求解相关的实际问题.(直观想象、逻辑推理)
教学重点:棱柱、棱锥、棱台、圆柱、圆锥、圆台、球的定义、结构特征及其实际应用.
教学难点:棱柱、棱锥、棱台、圆柱、圆锥、圆台、球的实际应用.
一
情景问题——北京故宫(导学)
一
情景问题——北京故宫(导学)
北京故宫是中国明清两代的皇家宫殿,旧称紫禁城,位于北京中轴线的中心.故宫以太和殿、中和殿、保和殿三大殿为中心,占地面积约72万平方米,建筑面积约15万平方米,有大小宫殿七十多座,一共有房间8707间 .
故宫是世界上现存规模最大、保存最为完整的木质结构古建筑群之一,是国家AAAAA级旅游景区,1961年被列为第一批全国重点文物保护单位,1987年被列为世界文化遗产.
(一)情 景
一
情景问题——北京故宫(导学)
各位同学,初中我们已经学习了三角形、四边形、圆等平面几何图形的相关知识及其应用.
但是人类生存在现实的三维空间中,我们需要突破平面的范围,研究空间中各种几何图形的形状、大小、度量及其性质.
那么你们能从美丽的故宫图片中找到那些三维空间中的几何图形,它们在数学上叫什么图形,有哪些分类和结构特征?
(二)问题
相信各位同学通过今天的学习,将能回答这一问题.
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
(一)观察
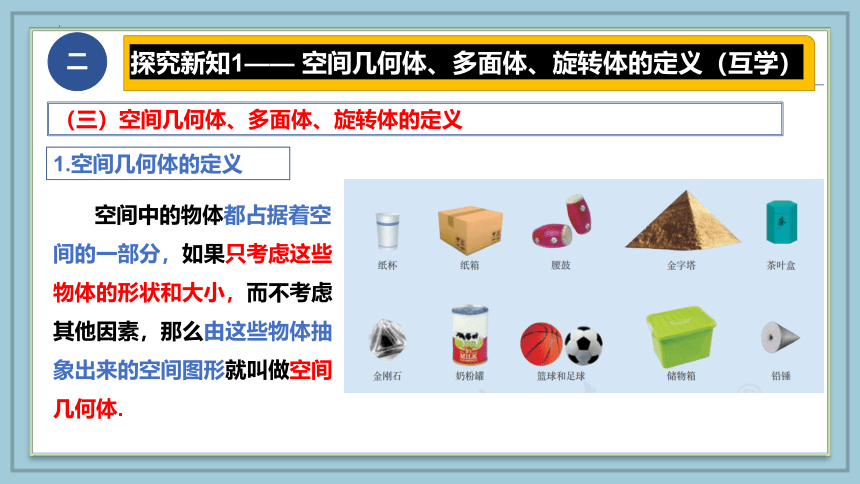
如图,这些图片中的物体具有怎样的形状 在日常生活中,我们把这些物体的形状叫做什么 如何描述它们的形状
纸 箱
金字塔
茶叶盒
金刚石
储物箱
纸 杯
腰 鼓
奶粉罐
篮球和足球
铅锤
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
(二)分析
观察发现:
1.这些物体都占据着空间的一部分;
2.纸箱、金字塔、茶叶盒、金刚石、储物箱等物体有相同的特点:围成它们的每个面都是平面图形,并且都是平面多边形;
纸 箱
金字塔
茶叶盒
金刚石
储物箱
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
(二)分析
观察发现:
3.纸杯、腰鼓、奶粉罐、篮球和足球、铅锤等物体也有相同的特点:围成它们的面不全是平面图形,有些面是曲面.
纸 杯
腰 鼓
奶粉罐
篮球和足球
铅锤
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
(三)空间几何体、多面体、旋转体的定义
1.空间几何体的定义
空间中的物体都占据着空间的一部分,如果只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
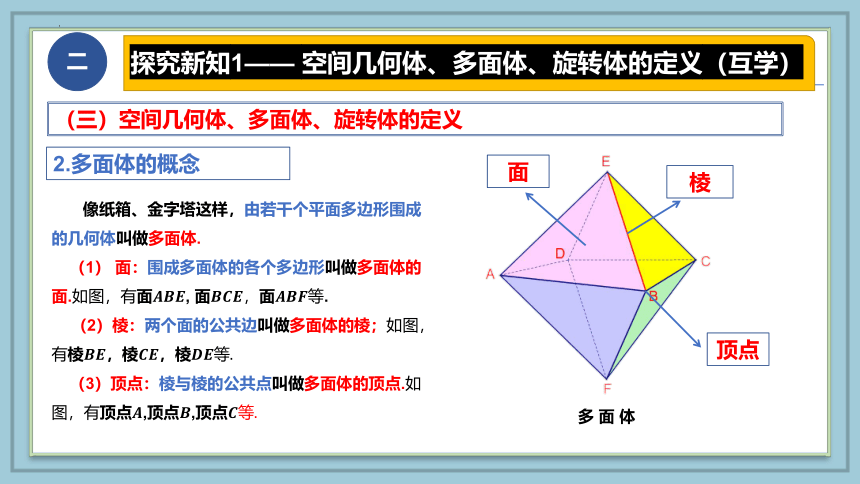
像纸箱、金字塔这样,由若干个平面多边形围成的几何体叫做多面体.
(1) 面:围成多面体的各个多边形叫做多面体的面.如图,有面, 面,面等.
(2)棱:两个面的公共边叫做多面体的棱;如图,有棱,棱,棱等.
(3)顶点:棱与棱的公共点叫做多面体的顶点.如图,有顶点,顶点,顶点等.
(三)空间几何体、多面体、旋转体的定义
2.多面体的概念
多 面 体
面
棱
顶点
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
像奶粉罐、篮球和足球这样,一条平面曲线(包括直线)绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体叫做旋转体,这条定直线叫做旋转体的轴 .
如图:圆柱体就是由矩形绕轴旋转而成.
(三)空间几何体、多面体、旋转体的定义
3.旋转体的概念
旋 转 体
旋 转 轴
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
(四)小结
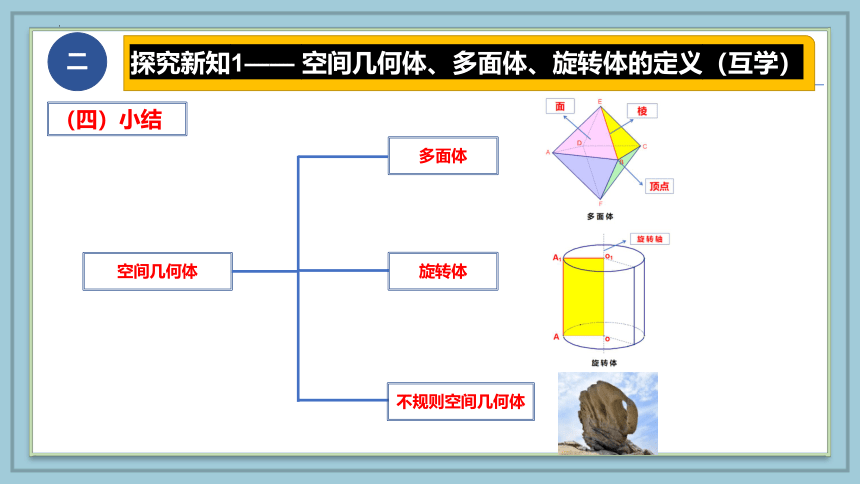
空间几何体
多面体
旋转体
不规则空间几何体
三
探究新知2——特殊的多面体之棱柱(互学)
观察下图中的多面体,想一想:这些多面体各有什么特点?它们分别由什么样的多边形围成?各个面之间的位置关系有什么特点?各条棱之间呢?
(一)观察
分析:直观上可以发现
(1)图中的每个多面体的上、下两面都是边数相同的全等多边形,且上、下两个面所在平面相互平行; (2)其余各面都是平行四边形; (3)各侧棱互相平行且相等.
三
探究新知2——特殊的多面体之棱柱(互学)
(二)棱柱的概念
如图,一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱.
1.底面(底):两个互相平行的面叫做棱柱的底面,它们是全等的多边形.
2.侧面:其余各面叫做棱柱的侧面,它们都是平行四边形.
3.侧棱:相邻侧面的公共边叫做棱柱的侧棱,它们都是相互平行且相等的线段.
侧棱
4.顶点:侧面与底面的公共顶点叫做棱柱的顶点.
棱 柱
底面
侧面
顶点
三
探究新知2——特殊的多面体之棱柱(互学)
(二)棱柱的概念
温馨提示
(1) 两个底面与平行于底面的截面是全等的多边形,如图(a)所示;
(2) 过不相邻的两条侧棱的截面是平行四边形,如图(b)所示;
(3) 有两个面平行,其余各面都是平行四边形的几何体不一定是棱柱,如图(c)所示,
三
探究新知2——特殊的多面体之棱柱(互学)
(三)棱柱的表示与分类
棱柱用表示底面各顶点的字母来表示,棱柱的底面可以是三角形、四边形、五边形……,我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱……
例如,右图中的棱柱分别表示为三棱柱,四棱柱,五棱柱
三
探究新知2——特殊的多面体之棱柱(互学)
(四)几种特殊的棱柱
1.直棱柱:一般地,我们把侧棱垂直于底面的棱柱叫做直棱柱.如右图中直四棱柱.
2.斜棱柱:侧棱不垂直于底面的棱柱叫做斜棱柱.如右图中斜三棱柱.
3.正棱柱:底面是正多边形的直棱柱叫做正棱柱.如右图中五棱柱.
4.平行六面体:底面是平行四边形的四棱柱也叫做平行六面体.如右图中平行六面体
四
小组合作、讨论交流1(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了棱柱的相关概念.
例1 下列说法正确的是( )
A.底面是矩形的四棱柱是长方体
B.有两个面平行,其余四个面都是平行四边形的四棱柱是平行六面体
C.棱柱的各个侧面都是平行四边形
D.有两个面平行,其余各面都是平行四边形的几何体是棱柱
五
成果展示1(迁移变通)
例1 下列说法正确的是 ( )
A.底面是矩形的四棱柱是长方体
B.有两个面平行,其余四个面都是平行四边形的四棱柱是平行六面体
C.棱柱的各个侧面都是平行四边形
D.有两个面平行,其余各面都是平行四边形的几何体是棱柱
解:(1)底面是矩形的四棱柱有可能是斜棱柱,不一定是长方体,故A错误;
(2)∵ 平行的两个面不一定是平行四边形,
∴有两个面平行,其余四个面都是平行四边形的四棱柱不一定是平行六面体,故B错误;
(3)根据棱柱的结构特征可知,C正确;
(4)如图所示的几何体,有两个面平行,其余各面都是平行四边形,但不是棱柱,故D错误.
答案:C
观察下图中的多面体,想一想:这些多面体有什么样的结构特征?它们分别由什么样的多边形围成?
(一)观察
分析:通过观察图形我们可以发现
这些多面体共同特点是都由平面图形围成,其中一个面为多边形,其他各面都是三角形,这些三角形有一个公共顶点.
六
探究新知3——特殊的多面体之棱锥(互学)
六
探究新知3——特殊的多面体之棱锥(互学)
(二)棱锥的概念
有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥.
1.底面:这个多边形面叫做棱锥的底面;
2.侧面:有公共顶点的各个三角形面叫做棱锥的侧面;
3.侧棱:相邻侧面的公共边叫做棱锥的侧棱;
侧棱
4.顶点:各侧面的公共顶点叫做棱锥的顶点.
顶点
棱 锥
底面
侧面
探究新知3——特殊的多面体之棱锥(互学)
(二)棱锥的概念
温馨提示:
对于棱锥要注意,有一个面是多边形,其余各面都是三角形的几何体不一定是棱锥,如图所示,必须强调其余各面是具有公共顶点的三角形.
六
六
探究新知3——特殊的多面体之棱锥(互学)
(三)棱锥的表示与分类
棱锥用表示顶点和底面各顶点的字母来表示,棱锥的底面可以是三角形、四边形、五边形……,我们把这样的棱锥分别叫做三棱锥、四棱锥、五棱锥……
注:其中三棱锥又叫四面体.
例如,右图中的棱锥分别表示为三棱锥(四面体),四棱锥,五棱锥
六
探究新知3——特殊的多面体之棱锥(互学)
(四)特殊的棱锥——正棱锥
底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥.
七
小组合作、讨论交流3(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了棱锥的相关概念.
例2 (多选)下列说法中,正确的是( )
A.棱锥的各个侧面都是三角形
B.四面体的任何一个面都可以作为棱锥的底面
C.棱锥的侧棱互相平行
D.有一个面是多边形,其余各面是三角形的几何体是棱锥
八
成果展示3(迁移变通)
例2 (多选)下列说法中,正确的是 ( )
A.棱锥的各个侧面都是三角形
B.四面体的任何一个面都可以作为棱锥的底面
C.棱锥的侧棱互相平行
D.有一个面是多边形,其余各面是三角形的几何体是棱锥
答案 A B
解:(1)由棱锥的定义知,棱锥的各个侧面都是三角形,故A正确;
(2)四面体是由四个三角形所围成的几何体,因此四面体的任何一个面都可以作为三棱锥的底面,故B正确;
(3)棱锥的侧棱交于一点,即不平行,故C错误;
(4)棱锥的侧面是有一个公共顶点的三角形,如图所示的几何体均满足条件,但不是棱锥,故D错误.
若用一个平行于棱锥底面的平面去截棱锥,直观感受一下,平面下方的几何体具有怎样的特点?
(一)观察
分析:通过观察图形我们可以发现
这一几何体的截面与棱锥的底面平行且相似,各侧面都是梯形.
九
探究新知4——特殊的多面体之棱台(互学)
(二)棱台的概念
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的那部分多面体叫做棱台.
1.上(下)底面:在棱台中,原棱锥的底面和截面分别叫做棱台的下底面和上底面,且上下底面是相似图形.
2.侧面:其余各个梯形面叫做棱台的侧面;
3.侧棱:相邻侧面的公共边叫做棱台的侧棱;
4.顶点:侧面与底面的公共顶点叫做棱台的顶点.
九
探究新知4——特殊的多面体之棱台(互学)
棱 台
上底面
下底面
侧面
顶点
侧棱
(二)棱台的概念
温馨提示:
棱台中各侧棱延长后必相交于一点,否则不是棱台.
九
探究新知4——特殊的多面体之棱台(互学)
九
(三)棱台的表示与分类
棱台用表示底面各顶点的字母来表示,由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……
例如,右图中的棱台分别表示为三棱台,四棱台,五棱锥
探究新知4——特殊的多面体之棱台(互学)
十
小组合作、讨论交流4(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了棱台的相关概念.
例3 (多选)下列选项中,不正确的是( )
A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台
B.有两个面平行且相似,其余各面都是梯形的多面体是棱台
C.有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台
D.棱台的侧棱延长后必交于一点
十一
成果展示4(迁移变通)
答案 ABC
解:(1)A中的平面不一定平行于底面,故A错;
(2)B,C可用反例去检验,如图所示,侧棱延长线不能相交于一点,故B,C错;
(3)由棱台的定义知,D正确.
例3 (多选)下列选项中,不正确的是( )
A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台
B.有两个面平行且相似,其余各面都是梯形的多面体是棱台
C.有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台
D.棱台的侧棱延长后必交于一点
根据上一节课的学习,我们知道下面的几何体都是旋转体,那么这些几何体中的曲面分别是由哪个平面图形旋转而得?
(一)观察
分析:通过观察图形我们可以发现
这些旋转体可由矩形绕一边所在的直线、直角三角形绕一直角边所在直线、直角梯形绕垂直于底边的一腰所在直线、半圆绕直径所在直线为轴旋转而成.
十二
探究新知5——特殊的旋转体(互学)
(二)圆柱的概念、结构特征与表示
以矩形的一边所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体叫做圆柱.
1.轴:旋转轴叫做圆柱的轴;
2.底面:垂直于轴的边旋转而成的圆面叫做圆柱的底面;
3.侧面:平行于轴的边旋转而成的曲面叫做圆柱的侧面;
4.母线:无论旋转到什么位置,平行于轴的边都叫做圆柱的母线.
十二
探究新知5——特殊的旋转体(互学)
轴
底
面
侧面
母线
圆 柱
注:圆柱用表示它的轴的字母表示,如图中的圆柱记作圆柱.
(三)圆锥的概念、结构特征与表示
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥.
1.轴:旋转轴叫做圆锥的轴;
2.底面:垂直于轴的边旋转而成的圆面叫做圆锥的底面;
3.侧面:直角三角形的斜边旋转而成的曲面叫做圆锥的侧面;
4.母线:无论旋转到什么位置,不垂直于轴的边都叫做圆锥的母线.
十二
探究新知5——特殊的旋转体(互学)
圆 锥
注:圆锥用表示它的轴的字母表示,如图中的圆锥记作圆锥.
底
面
轴
母线
侧面
(三)圆台的概念、结构特征与表示
用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.
1.轴:旋转轴叫做圆台的轴;
2.底面:垂直于轴的边旋转而成的圆面叫做圆台的底面;
3.侧面:不垂直于轴的边旋转一周所形成的曲面叫做圆台的侧面;
4.母线:无论旋转到什么位置,不垂直于轴的边都叫做圆台的母线.
十二
探究新知5——特殊的旋转体(互学)
圆 台
注:圆台用表示它的轴的字母表示,如图中的圆台记作圆台.
母线
底
面
轴
侧面
(四)球的概念、结构特征与表示
半圆以它的直径所在直线为旋转轴,旋转一周形成的曲面叫做球面,球面所围成的旋转体叫做球体,简称球.
1.球心:半圆的圆心叫做球的球心;
2.半径:连接球心和球面上任意一点的线段叫做球的半径;
3.直径:连接球面上两点并经过球心的线段叫做球的直径;
十二
探究新知5——特殊的旋转体(互学)
球
注:球常用表示球心的字母表示,如图中的球记作球.
半径
直径
球心
十三
小组合作、讨论交流5(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了旋转体的相关概念.
例4 下列说法正确的是 (填序号).
①以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台;
②圆柱、圆锥、圆台的底面都是圆;
③以等腰三角形的底边上的高线所在的直线为旋转轴,其余各边旋转一周形成的曲面所围成的几何体是圆锥;
④半圆面绕其直径所在直线旋转一周形成球;
⑤用一个平面去截球,得到的截面是一个圆面.
十四
成果展示5(迁移变通)
答案 ③④⑤
解:①以直角梯形垂直于底边的一腰所在直线为轴旋转一周可得到圆台;
②它们的底面为圆面;
③④⑤正确.
例4 下列说法正确的是 (填序号).
①以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台;
②圆柱、圆锥、圆台的底面都是圆;
③以等腰三角形的底边上的高线所在的直线为旋转轴,其余各边旋转一周形成的曲面所围成的几何体是圆锥;
④半圆面绕其直径所在直线旋转一周形成球;
⑤用一个平面去截球,得到的截面是一个圆面.
观察下图中的几何体,想一想:它们都是由那些简单几何体组合而成的?
(一)观察
分析:通过观察图形我们可以发现
(1)第一个几何体是由球体与圆柱体拼接而成;
(2)第二个几何体是由正方体截去(或挖去)一个三棱锥而得到的.
十五
探究新知6——简单组合体(互学)
(二)简单组合体的概念与构成形式
1.定义:由简单几何体组合而成的几何体叫做简单组合体.
十五
探究新知6——简单组合体(互学)
2.构成形式
(1)一种是由简单几何体拼接而成的,如图1;
(2)另一种是由简单几何体截去或挖去一部分而成的,如图2.
十六
小组合作、讨论交流6(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了简单组合体的概念.
例5 如图,以直角梯形的下底所在直线为轴,其余三边旋转一周形成的面围成一个几何体,说出这个几何体的结构特征.
十七
成果展示6(迁移变通)
解:几何体如图(2)所示,其中,垂足为.
这个几何体是由圆柱和圆锥组合而成的.其中圆柱的底面分别是和,侧面是由梯形的上底绕轴旋转形成的;圆锥的底面是,侧面是由梯形的边绕轴旋转而成的.
例5 如图,以直角梯形的下底所在直线为轴,其余三边旋转一周形成的面围成一个几何体,说出这个几何体的结构特征.
课堂小结
十八
本节课我们学习了哪些内容?
1.利用实物,认识与理解了空间几何体、简单组合体的概念与分类.(直观想象)
2.理解与掌握了棱柱、棱锥、棱台、圆柱、圆锥、圆台、球的定义及其结构特征,并能应用其求解相关的实际问题.(直观想象、逻辑推理)
十九
学生自评
请小老师组对所负责组员的课堂表现进行评价
二十
家庭作业
1.整理导学案中本节课知识点并记背;
2.完成导学案上相关题型.
人教版必修第二册A版
8.1《 基本立体图形 》
( 3 课 时 )
教学目标
学习目标:1.利用实物,认识与理解空间几何体、简单几何体的概念与分类.(直观想象)
2.理解与掌握棱柱、棱锥、棱台、圆柱、圆锥、圆台、球的定义及其结构特征,并能应用其求解相关的实际问题.(直观想象、逻辑推理)
教学重点:棱柱、棱锥、棱台、圆柱、圆锥、圆台、球的定义、结构特征及其实际应用.
教学难点:棱柱、棱锥、棱台、圆柱、圆锥、圆台、球的实际应用.
一
情景问题——北京故宫(导学)
一
情景问题——北京故宫(导学)
北京故宫是中国明清两代的皇家宫殿,旧称紫禁城,位于北京中轴线的中心.故宫以太和殿、中和殿、保和殿三大殿为中心,占地面积约72万平方米,建筑面积约15万平方米,有大小宫殿七十多座,一共有房间8707间 .
故宫是世界上现存规模最大、保存最为完整的木质结构古建筑群之一,是国家AAAAA级旅游景区,1961年被列为第一批全国重点文物保护单位,1987年被列为世界文化遗产.
(一)情 景
一
情景问题——北京故宫(导学)
各位同学,初中我们已经学习了三角形、四边形、圆等平面几何图形的相关知识及其应用.
但是人类生存在现实的三维空间中,我们需要突破平面的范围,研究空间中各种几何图形的形状、大小、度量及其性质.
那么你们能从美丽的故宫图片中找到那些三维空间中的几何图形,它们在数学上叫什么图形,有哪些分类和结构特征?
(二)问题
相信各位同学通过今天的学习,将能回答这一问题.
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
(一)观察
如图,这些图片中的物体具有怎样的形状 在日常生活中,我们把这些物体的形状叫做什么 如何描述它们的形状
纸 箱
金字塔
茶叶盒
金刚石
储物箱
纸 杯
腰 鼓
奶粉罐
篮球和足球
铅锤
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
(二)分析
观察发现:
1.这些物体都占据着空间的一部分;
2.纸箱、金字塔、茶叶盒、金刚石、储物箱等物体有相同的特点:围成它们的每个面都是平面图形,并且都是平面多边形;
纸 箱
金字塔
茶叶盒
金刚石
储物箱
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
(二)分析
观察发现:
3.纸杯、腰鼓、奶粉罐、篮球和足球、铅锤等物体也有相同的特点:围成它们的面不全是平面图形,有些面是曲面.
纸 杯
腰 鼓
奶粉罐
篮球和足球
铅锤
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
(三)空间几何体、多面体、旋转体的定义
1.空间几何体的定义
空间中的物体都占据着空间的一部分,如果只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
像纸箱、金字塔这样,由若干个平面多边形围成的几何体叫做多面体.
(1) 面:围成多面体的各个多边形叫做多面体的面.如图,有面, 面,面等.
(2)棱:两个面的公共边叫做多面体的棱;如图,有棱,棱,棱等.
(3)顶点:棱与棱的公共点叫做多面体的顶点.如图,有顶点,顶点,顶点等.
(三)空间几何体、多面体、旋转体的定义
2.多面体的概念
多 面 体
面
棱
顶点
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
像奶粉罐、篮球和足球这样,一条平面曲线(包括直线)绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体叫做旋转体,这条定直线叫做旋转体的轴 .
如图:圆柱体就是由矩形绕轴旋转而成.
(三)空间几何体、多面体、旋转体的定义
3.旋转体的概念
旋 转 体
旋 转 轴
二
探究新知1—— 空间几何体、多面体、旋转体的定义(互学)
(四)小结
空间几何体
多面体
旋转体
不规则空间几何体
三
探究新知2——特殊的多面体之棱柱(互学)
观察下图中的多面体,想一想:这些多面体各有什么特点?它们分别由什么样的多边形围成?各个面之间的位置关系有什么特点?各条棱之间呢?
(一)观察
分析:直观上可以发现
(1)图中的每个多面体的上、下两面都是边数相同的全等多边形,且上、下两个面所在平面相互平行; (2)其余各面都是平行四边形; (3)各侧棱互相平行且相等.
三
探究新知2——特殊的多面体之棱柱(互学)
(二)棱柱的概念
如图,一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱.
1.底面(底):两个互相平行的面叫做棱柱的底面,它们是全等的多边形.
2.侧面:其余各面叫做棱柱的侧面,它们都是平行四边形.
3.侧棱:相邻侧面的公共边叫做棱柱的侧棱,它们都是相互平行且相等的线段.
侧棱
4.顶点:侧面与底面的公共顶点叫做棱柱的顶点.
棱 柱
底面
侧面
顶点
三
探究新知2——特殊的多面体之棱柱(互学)
(二)棱柱的概念
温馨提示
(1) 两个底面与平行于底面的截面是全等的多边形,如图(a)所示;
(2) 过不相邻的两条侧棱的截面是平行四边形,如图(b)所示;
(3) 有两个面平行,其余各面都是平行四边形的几何体不一定是棱柱,如图(c)所示,
三
探究新知2——特殊的多面体之棱柱(互学)
(三)棱柱的表示与分类
棱柱用表示底面各顶点的字母来表示,棱柱的底面可以是三角形、四边形、五边形……,我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱……
例如,右图中的棱柱分别表示为三棱柱,四棱柱,五棱柱
三
探究新知2——特殊的多面体之棱柱(互学)
(四)几种特殊的棱柱
1.直棱柱:一般地,我们把侧棱垂直于底面的棱柱叫做直棱柱.如右图中直四棱柱.
2.斜棱柱:侧棱不垂直于底面的棱柱叫做斜棱柱.如右图中斜三棱柱.
3.正棱柱:底面是正多边形的直棱柱叫做正棱柱.如右图中五棱柱.
4.平行六面体:底面是平行四边形的四棱柱也叫做平行六面体.如右图中平行六面体
四
小组合作、讨论交流1(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了棱柱的相关概念.
例1 下列说法正确的是( )
A.底面是矩形的四棱柱是长方体
B.有两个面平行,其余四个面都是平行四边形的四棱柱是平行六面体
C.棱柱的各个侧面都是平行四边形
D.有两个面平行,其余各面都是平行四边形的几何体是棱柱
五
成果展示1(迁移变通)
例1 下列说法正确的是 ( )
A.底面是矩形的四棱柱是长方体
B.有两个面平行,其余四个面都是平行四边形的四棱柱是平行六面体
C.棱柱的各个侧面都是平行四边形
D.有两个面平行,其余各面都是平行四边形的几何体是棱柱
解:(1)底面是矩形的四棱柱有可能是斜棱柱,不一定是长方体,故A错误;
(2)∵ 平行的两个面不一定是平行四边形,
∴有两个面平行,其余四个面都是平行四边形的四棱柱不一定是平行六面体,故B错误;
(3)根据棱柱的结构特征可知,C正确;
(4)如图所示的几何体,有两个面平行,其余各面都是平行四边形,但不是棱柱,故D错误.
答案:C
观察下图中的多面体,想一想:这些多面体有什么样的结构特征?它们分别由什么样的多边形围成?
(一)观察
分析:通过观察图形我们可以发现
这些多面体共同特点是都由平面图形围成,其中一个面为多边形,其他各面都是三角形,这些三角形有一个公共顶点.
六
探究新知3——特殊的多面体之棱锥(互学)
六
探究新知3——特殊的多面体之棱锥(互学)
(二)棱锥的概念
有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥.
1.底面:这个多边形面叫做棱锥的底面;
2.侧面:有公共顶点的各个三角形面叫做棱锥的侧面;
3.侧棱:相邻侧面的公共边叫做棱锥的侧棱;
侧棱
4.顶点:各侧面的公共顶点叫做棱锥的顶点.
顶点
棱 锥
底面
侧面
探究新知3——特殊的多面体之棱锥(互学)
(二)棱锥的概念
温馨提示:
对于棱锥要注意,有一个面是多边形,其余各面都是三角形的几何体不一定是棱锥,如图所示,必须强调其余各面是具有公共顶点的三角形.
六
六
探究新知3——特殊的多面体之棱锥(互学)
(三)棱锥的表示与分类
棱锥用表示顶点和底面各顶点的字母来表示,棱锥的底面可以是三角形、四边形、五边形……,我们把这样的棱锥分别叫做三棱锥、四棱锥、五棱锥……
注:其中三棱锥又叫四面体.
例如,右图中的棱锥分别表示为三棱锥(四面体),四棱锥,五棱锥
六
探究新知3——特殊的多面体之棱锥(互学)
(四)特殊的棱锥——正棱锥
底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥.
七
小组合作、讨论交流3(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了棱锥的相关概念.
例2 (多选)下列说法中,正确的是( )
A.棱锥的各个侧面都是三角形
B.四面体的任何一个面都可以作为棱锥的底面
C.棱锥的侧棱互相平行
D.有一个面是多边形,其余各面是三角形的几何体是棱锥
八
成果展示3(迁移变通)
例2 (多选)下列说法中,正确的是 ( )
A.棱锥的各个侧面都是三角形
B.四面体的任何一个面都可以作为棱锥的底面
C.棱锥的侧棱互相平行
D.有一个面是多边形,其余各面是三角形的几何体是棱锥
答案 A B
解:(1)由棱锥的定义知,棱锥的各个侧面都是三角形,故A正确;
(2)四面体是由四个三角形所围成的几何体,因此四面体的任何一个面都可以作为三棱锥的底面,故B正确;
(3)棱锥的侧棱交于一点,即不平行,故C错误;
(4)棱锥的侧面是有一个公共顶点的三角形,如图所示的几何体均满足条件,但不是棱锥,故D错误.
若用一个平行于棱锥底面的平面去截棱锥,直观感受一下,平面下方的几何体具有怎样的特点?
(一)观察
分析:通过观察图形我们可以发现
这一几何体的截面与棱锥的底面平行且相似,各侧面都是梯形.
九
探究新知4——特殊的多面体之棱台(互学)
(二)棱台的概念
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的那部分多面体叫做棱台.
1.上(下)底面:在棱台中,原棱锥的底面和截面分别叫做棱台的下底面和上底面,且上下底面是相似图形.
2.侧面:其余各个梯形面叫做棱台的侧面;
3.侧棱:相邻侧面的公共边叫做棱台的侧棱;
4.顶点:侧面与底面的公共顶点叫做棱台的顶点.
九
探究新知4——特殊的多面体之棱台(互学)
棱 台
上底面
下底面
侧面
顶点
侧棱
(二)棱台的概念
温馨提示:
棱台中各侧棱延长后必相交于一点,否则不是棱台.
九
探究新知4——特殊的多面体之棱台(互学)
九
(三)棱台的表示与分类
棱台用表示底面各顶点的字母来表示,由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……
例如,右图中的棱台分别表示为三棱台,四棱台,五棱锥
探究新知4——特殊的多面体之棱台(互学)
十
小组合作、讨论交流4(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了棱台的相关概念.
例3 (多选)下列选项中,不正确的是( )
A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台
B.有两个面平行且相似,其余各面都是梯形的多面体是棱台
C.有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台
D.棱台的侧棱延长后必交于一点
十一
成果展示4(迁移变通)
答案 ABC
解:(1)A中的平面不一定平行于底面,故A错;
(2)B,C可用反例去检验,如图所示,侧棱延长线不能相交于一点,故B,C错;
(3)由棱台的定义知,D正确.
例3 (多选)下列选项中,不正确的是( )
A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台
B.有两个面平行且相似,其余各面都是梯形的多面体是棱台
C.有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台
D.棱台的侧棱延长后必交于一点
根据上一节课的学习,我们知道下面的几何体都是旋转体,那么这些几何体中的曲面分别是由哪个平面图形旋转而得?
(一)观察
分析:通过观察图形我们可以发现
这些旋转体可由矩形绕一边所在的直线、直角三角形绕一直角边所在直线、直角梯形绕垂直于底边的一腰所在直线、半圆绕直径所在直线为轴旋转而成.
十二
探究新知5——特殊的旋转体(互学)
(二)圆柱的概念、结构特征与表示
以矩形的一边所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体叫做圆柱.
1.轴:旋转轴叫做圆柱的轴;
2.底面:垂直于轴的边旋转而成的圆面叫做圆柱的底面;
3.侧面:平行于轴的边旋转而成的曲面叫做圆柱的侧面;
4.母线:无论旋转到什么位置,平行于轴的边都叫做圆柱的母线.
十二
探究新知5——特殊的旋转体(互学)
轴
底
面
侧面
母线
圆 柱
注:圆柱用表示它的轴的字母表示,如图中的圆柱记作圆柱.
(三)圆锥的概念、结构特征与表示
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥.
1.轴:旋转轴叫做圆锥的轴;
2.底面:垂直于轴的边旋转而成的圆面叫做圆锥的底面;
3.侧面:直角三角形的斜边旋转而成的曲面叫做圆锥的侧面;
4.母线:无论旋转到什么位置,不垂直于轴的边都叫做圆锥的母线.
十二
探究新知5——特殊的旋转体(互学)
圆 锥
注:圆锥用表示它的轴的字母表示,如图中的圆锥记作圆锥.
底
面
轴
母线
侧面
(三)圆台的概念、结构特征与表示
用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.
1.轴:旋转轴叫做圆台的轴;
2.底面:垂直于轴的边旋转而成的圆面叫做圆台的底面;
3.侧面:不垂直于轴的边旋转一周所形成的曲面叫做圆台的侧面;
4.母线:无论旋转到什么位置,不垂直于轴的边都叫做圆台的母线.
十二
探究新知5——特殊的旋转体(互学)
圆 台
注:圆台用表示它的轴的字母表示,如图中的圆台记作圆台.
母线
底
面
轴
侧面
(四)球的概念、结构特征与表示
半圆以它的直径所在直线为旋转轴,旋转一周形成的曲面叫做球面,球面所围成的旋转体叫做球体,简称球.
1.球心:半圆的圆心叫做球的球心;
2.半径:连接球心和球面上任意一点的线段叫做球的半径;
3.直径:连接球面上两点并经过球心的线段叫做球的直径;
十二
探究新知5——特殊的旋转体(互学)
球
注:球常用表示球心的字母表示,如图中的球记作球.
半径
直径
球心
十三
小组合作、讨论交流5(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了旋转体的相关概念.
例4 下列说法正确的是 (填序号).
①以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台;
②圆柱、圆锥、圆台的底面都是圆;
③以等腰三角形的底边上的高线所在的直线为旋转轴,其余各边旋转一周形成的曲面所围成的几何体是圆锥;
④半圆面绕其直径所在直线旋转一周形成球;
⑤用一个平面去截球,得到的截面是一个圆面.
十四
成果展示5(迁移变通)
答案 ③④⑤
解:①以直角梯形垂直于底边的一腰所在直线为轴旋转一周可得到圆台;
②它们的底面为圆面;
③④⑤正确.
例4 下列说法正确的是 (填序号).
①以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台;
②圆柱、圆锥、圆台的底面都是圆;
③以等腰三角形的底边上的高线所在的直线为旋转轴,其余各边旋转一周形成的曲面所围成的几何体是圆锥;
④半圆面绕其直径所在直线旋转一周形成球;
⑤用一个平面去截球,得到的截面是一个圆面.
观察下图中的几何体,想一想:它们都是由那些简单几何体组合而成的?
(一)观察
分析:通过观察图形我们可以发现
(1)第一个几何体是由球体与圆柱体拼接而成;
(2)第二个几何体是由正方体截去(或挖去)一个三棱锥而得到的.
十五
探究新知6——简单组合体(互学)
(二)简单组合体的概念与构成形式
1.定义:由简单几何体组合而成的几何体叫做简单组合体.
十五
探究新知6——简单组合体(互学)
2.构成形式
(1)一种是由简单几何体拼接而成的,如图1;
(2)另一种是由简单几何体截去或挖去一部分而成的,如图2.
十六
小组合作、讨论交流6(自学)
各位同学,请大家每4个人组成一组,分别交流讨论后,解决下列问题:
方法提示:这道题考察了简单组合体的概念.
例5 如图,以直角梯形的下底所在直线为轴,其余三边旋转一周形成的面围成一个几何体,说出这个几何体的结构特征.
十七
成果展示6(迁移变通)
解:几何体如图(2)所示,其中,垂足为.
这个几何体是由圆柱和圆锥组合而成的.其中圆柱的底面分别是和,侧面是由梯形的上底绕轴旋转形成的;圆锥的底面是,侧面是由梯形的边绕轴旋转而成的.
例5 如图,以直角梯形的下底所在直线为轴,其余三边旋转一周形成的面围成一个几何体,说出这个几何体的结构特征.
课堂小结
十八
本节课我们学习了哪些内容?
1.利用实物,认识与理解了空间几何体、简单组合体的概念与分类.(直观想象)
2.理解与掌握了棱柱、棱锥、棱台、圆柱、圆锥、圆台、球的定义及其结构特征,并能应用其求解相关的实际问题.(直观想象、逻辑推理)
十九
学生自评
请小老师组对所负责组员的课堂表现进行评价
二十
家庭作业
1.整理导学案中本节课知识点并记背;
2.完成导学案上相关题型.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
