2023-2024学年广西南宁三中八年级(下)开学数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年广西南宁三中八年级(下)开学数学试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 170.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 00:00:00 | ||
图片预览




文档简介
2023-2024学年广西南宁三中八年级(下)开学数学试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.代数式的意义可以是( )
A. 与的和 B. 与的差 C. 与的积 D. 与的商
2.下面四个化学仪器示意图中,是轴对称图形的是( )
A. B. C. D.
3.光年是天文学上的一种距离单位,一光年是指光在一年内走过的路程,约等于,下列正确的是( )
A. B.
C. 是一个位数 D. 是一个位数
4.下列长度的三条线段,能组成三角形的是( )
A. ,, B. ,, C. ,, D. ,,
5.化简的结果是( )
A. B. C. D.
6.若是一个完全平方式,则的值是( )
A. B. C. 或 D. 或
7.如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点,点为焦点若,,则的度数为( )
A. B. C. D.
8.如图,在中,,,的平分线交于,于点,若,则( )
A.
B.
C.
D.
9.千里江山图是宋代王希孟的作品,如图,它的局部画面装裱前是一个长为米,宽为米的矩形,装裱后,整幅图画宽与长的比是:,且四周边衬的宽度相等,则边衬的宽度应是多少米?设边衬的宽度为米,根据题意可列方程( )
A. B. C. D.
10.如图,将两块相同的三角板含角按图中所示位置摆放,若交于,交于,交于,则下列结论中错误的是( )
A. B.
C. ≌ D.
11.若为任意整数,则的值总能( )
A. 被整除 B. 被整除 C. 被整除 D. 被整除
12.在多项式其中中,对相邻的两个字母间任意添加绝对值符号,添加绝对值符号后仍只有减法运算,然后进行去绝对值运算,称此为“绝对操作”例如:,,下列说法:
存在“绝对操作”,使其运算结果与原多项式相等;
不存在“绝对操作”,使其运算结果与原多项式之和为;
所有的“绝对操作”共有种不同运算结果.
其中正确的个数是( )
A. B. C. D.
二、填空题:本题共6小题,每小题2分,共12分。
13.使得分式有意义的条件是______.
14.一个多边形外角和是内角和的,则这个多边形的边数为______.
15.如图,在中,,,点为上一点,连接过点作于点,过点作交的延长线于点若,,则的长度为______.
16.已知,且,则的值为______.
17.若关于的一元一次不等式组至少有个整数解,且关于的分式方程有非负整数解,则所有满足条件的整数的值之和是______.
18.如果一个四位自然数的各数位上的数字互不相等且均不为,满足,那么称这个四位数为“递减数”例如:四位数,,是“递减数”;又如:四位数,,不是“递减数”若一个“递减数”为,则这个数为;若一个“递减数”的前三个数字组成的三位数与后三个数字组成的三位数的和能被整除,则满足条件的数的最大值是______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:.
20.本小题分
先化简,再求值:,其中.
21.本小题分
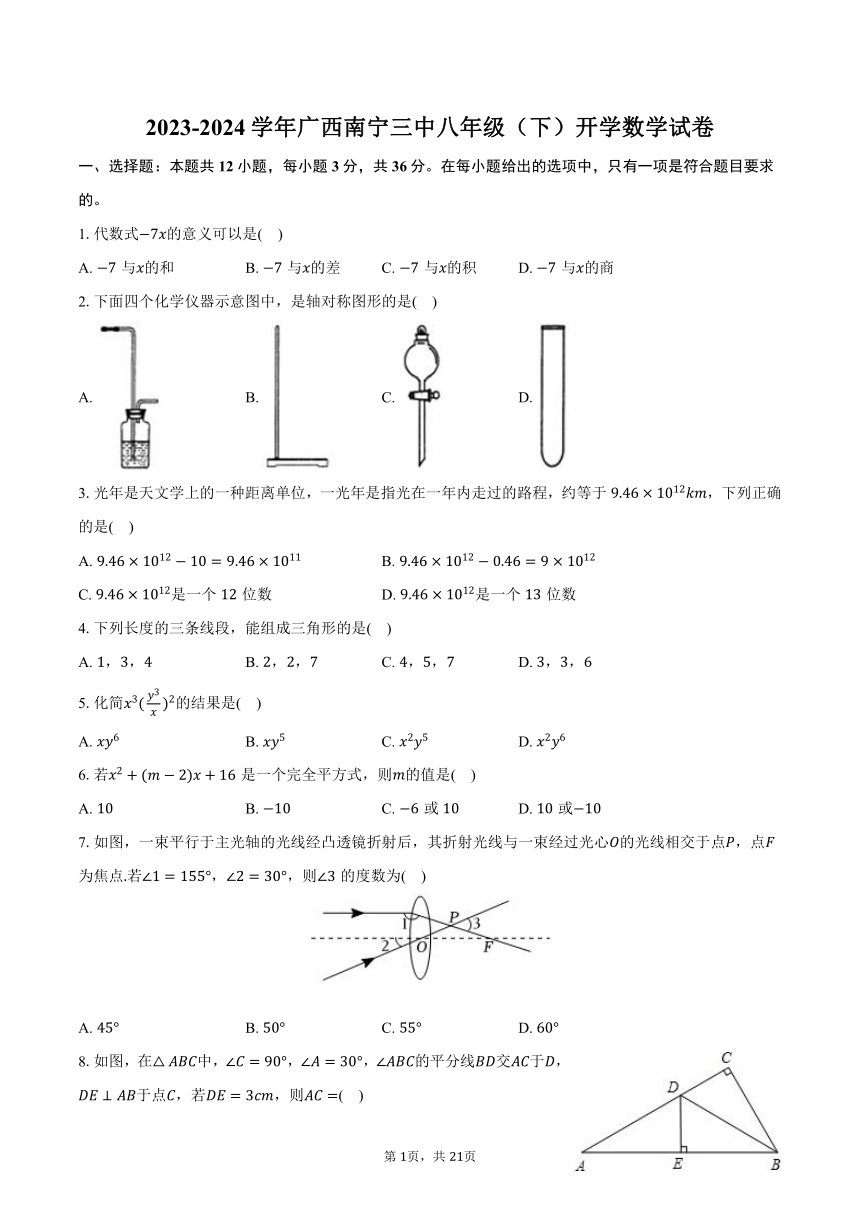
如图,已知的三个顶点的坐标分别是,,.
画出与关于轴对称的,并直接写出,,的坐标;
在轴上有一点,使得≌,请直接写出点的坐标.
22.本小题分
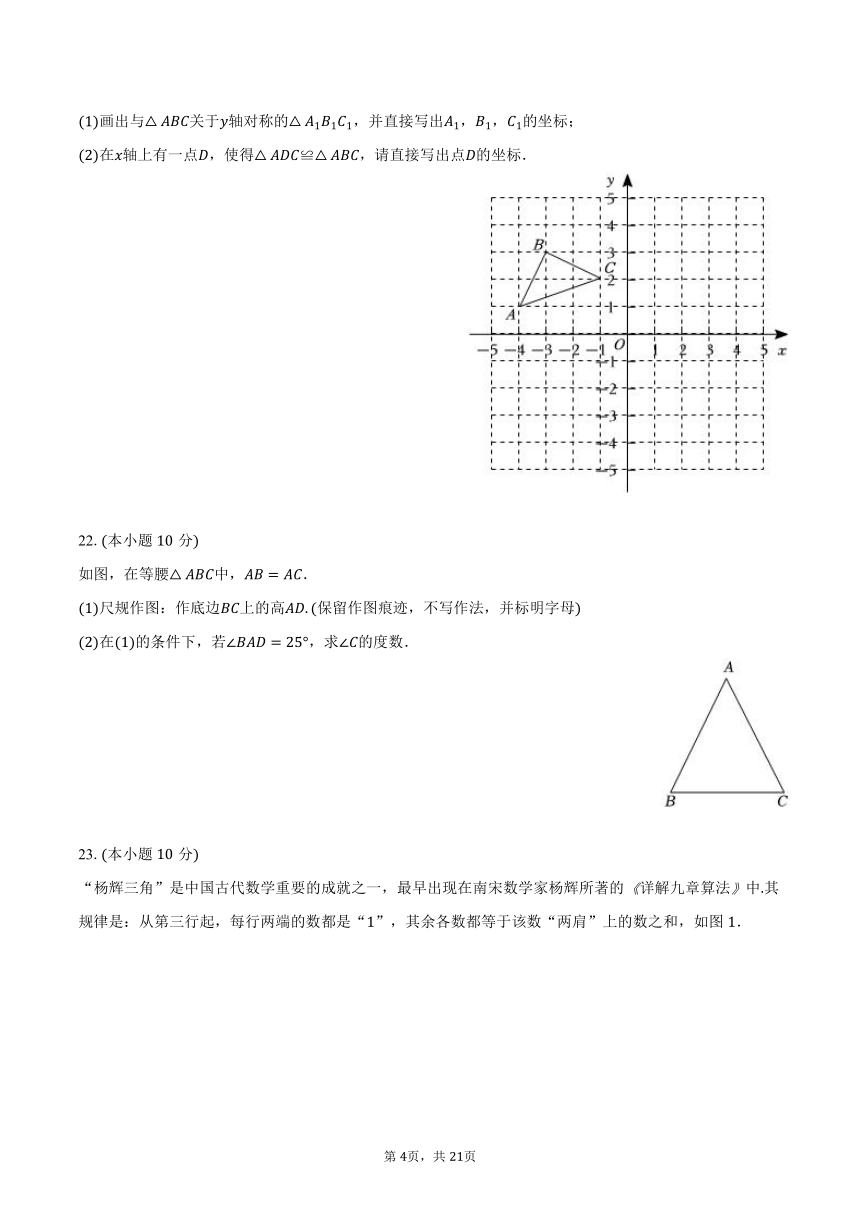
如图,在等腰中,.
尺规作图:作底边上的高保留作图痕迹,不写作法,并标明字母
在的条件下,若,求的度数.
23.本小题分
“杨辉三角”是中国古代数学重要的成就之一,最早出现在南宋数学家杨辉所著的详解九章算法中其规律是:从第三行起,每行两端的数都是“”,其余各数都等于该数“两肩”上的数之和,如图.
求图中第行第个数是______;
求图中前行所有的数字之和;
“杨辉三角”的应用很广泛,例如“堆垛术”,图中的立体图形是由若干形状、大小相同的圆球摆放而成,从上至下每层小球的个数依次为:,,,,记第层的圆球数记,求的值.
24.本小题分
科技改变世界,为提高快递包裹分拣效率,物流公司引进了快递自动分拣流水线,一条某型号的自动分拣流水线每小时分拣的包裹量是名工人每小时分拣包裹量的倍,分拣件包裹,用一条自动分拣流水线分拣比名工人分拣少用小时.
一条自动分拣流水线每小时能分拣多少件包裹?
新年将至,某转运中心预计每日需分拣的包裹量高达件,现准备购买该型号的自动分拣流水线进行小时作业,则至少应购买多少条?
25.本小题分
【问题情境】如图,与都是等边三角形,连接,,点,分别是,的中点,连接,,.
【猜想证明】请证明:
求证:;
求证:是等边三角形.
【类比探究】如图,与都是等腰直角三角形,连接,,点,分别是,的中点,连接,请探究:
若点恰好也是的中点,且,求的面积.
26.本小题分
综合与实践
【思考尝试】
数学活动课上,老师出示了一个问题:在平面直角坐标系中,点关于轴的对称点的坐标为______;
【实践探究】
小睿受此问题启发,一般化思考并提出新的问题:如图,在平面直角坐标系中,点的坐标为,求点关于直线的对称点的坐标用含,的式子表示;
【拓展迁移】
小博深入研究小睿提出的这个问题,提出新的探究点,并进行了探究:如图,在平面直角坐标系中,点的坐标为,直接写出点关于直线的对称点的坐标用含的式子表示小博经过探究得出直线上任意一点的横坐标与纵坐标的比都是:,点的纵坐标为,请帮助小博完成问题.
答案和解析
1.【答案】
【解析】解:代数式的意义可以是与的积.
故选:.
直接利用代数式的意义分析得出答案.
此题主要考查了代数式,掌握代数式是由运算符号加、减、乘、除、乘方、开方把数或表示数的字母连接而成的式子是解题关键.
2.【答案】
【解析】【试题解析】
解:、不是轴对称图形,故本选项不合题意;
B、不是轴对称图形,故本选项不合题意;
C、不是轴对称图形,故本选项不合题意;
D、是轴对称图形,故本选项符合题意.
故选:.
根据轴对称图形的概念对各选项分析判断即可得解.
本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
3.【答案】
【解析】解:是一个位数.
故选:.
科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正数;当原数的绝对值时,是负数.
此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.
4.【答案】
【解析】解:,,,不能组成三角形,故A选项不符合题意;
,,,不能组成三角形,故B不符合题意;
,,,能组成三角形,故C符合题意;
,,,不能组成三角形,故D不符合题意,
故选:.
根据三角形的三边关系分别判断即可.
本题考查了三角形的三边关系,熟练掌握三角形的三边关系是解题的关键.
5.【答案】
【解析】解:
,
故选:.
先根据分式的乘方法则计算,再根据分式的乘法法则计算.
本题考查的是分式的乘除法,掌握分式的乘法法则、乘方法则是解题的关键.
6.【答案】
【解析】解:是一个完全平方式,
或,
,
或.
故选:.
利用完全平方公式得到或,从而得到,然后解关于的方程.
本题考查了完全平方式:对于一个具有若干个简单变元的整式,如果存在另一个实系数整式,使,则称是完全平方式,即.
7.【答案】
【解析】解:,
,
,
,
,
.
故选:.
由平行线的性质求出,由对顶角的性质得到,由三角形外角的性质即可求出的度数.
本题考查平行线的性质,三角形外角的性质,对顶角的性质,关键是由平行线的性质求出的度数,由对顶角的性质得到的度数,由三角形外角的性质即可解决问题.
8.【答案】
【解析】解:是的平分线,,,
;
,,
,
是的平分线,
,
,
又,
,
是等腰三角形,
,
.
故选:.
首先根据角平分线的性质,可得;然后判断出是等腰三角形,求出的长度,进而求出的长度是多少即可.
此题主要考查了角平分线的性质和应用,以及含度角的直角三角形的性质和应用,要熟练掌握.
9.【答案】
【解析】【解答】
解:由题意可得,
,
故选:.
【分析】
根据题意可知,装裱后的长为,宽为,再根据整幅图画宽与长的比是:,即可得到相应的方程.
本题考查由实际问题抽象出分式方程,解答本题的关键是明确题意,列出相应的分式方程.
10.【答案】
【解析】解:≌,
,,,
,故A正确;
在与中
≌,故C正确;
,故D正确;
故选:.
根据全等三角形的判定和性质判断即可.
此题考查了全等三角形的判定和性质,解题的关键是综合利用全等三角形的判定和性质进行解答.
11.【答案】
【解析】【分析】
先根据完全平方公式进行计算,再合并同类项,分解因式后再逐个判断即可.
本题考查了因式分解的应用,能求出是解此题的关键.
【解答】
解:
,
为任意整数,
的值总能被整除,
故选:.
12.【答案】
【解析】【分析】
根据给定的定义,举出符合条件的说法和说法需要对绝对操作分析添加一个和两个绝对值的情况,并将结果进行比较排除相等的结果,汇总得出答案.
本题考查新定义题型,根据所给的定义,举出符合条件的代数式进行情况讨论;
需要注意去绝对值时的符号,和所有结果可能的比较.主要考查绝对值计算和分类讨论思想的应用.
【解答】
解:,故说法正确.
若使其运算结果与原多项式之和为,需出现,
显然无论怎么添加绝对值,都无法使的符号为负号,故说法正确.
当添加一个绝对值时,共有种情况,分别是;;;当添加两个绝对值时,共有种情况,分别是;;共有种情况;
有两对运算结果相同,故共有种不同运算结果,故说法错误.
综上,说法正确的有共个.
故选:.
13.【答案】
【解析】解:由题意得:,
解得:,
故答案为:.
根据分式有意义的条件可得:,再解即可.
此题主要考查了分式有意义的条件,关键是掌握分式有意义的条件是分母不等于零.
14.【答案】
【解析】解:根据题意可得:,
解得:,
故答案为:.
多边形的内角和定理为,多边形的外角和为,根据题意列出方程求出的值.
本题主要考查的是多边形的内角和公式以及外角和定理,属于基础题型.记忆理解并应用这两个公式是解题的关键.
15.【答案】
【解析】解:,,
,
,
,
,
,
在和中,
,
≌,
,,
,,
,,
,
故答案为:.
先证明≌,根据全等三角形的性质可得,,进一步可得的长.
本题考查了全等三角形的判定和性质,等腰直角三角形的性质,熟练掌握全等三角形的判定方法是解题的关键.
16.【答案】
【解析】解:,
,
,
.
故答案为:.
根据,可得,再代入即可求出答案.
本题考查了分式的加减法和分式的值,熟练掌握分式的运算法则是关键.
17.【答案】
【解析】解:解不等式组,得,
至少有个整数解,
,
,
解分式方程,
得,
的值是非负整数,,
当时,,
当时,,
当时,,
是分式方程的增根,
舍去,
满足条件的的值有和,
,
所有满足条件的整数的值之和是.
故答案为:.
先解不等式组,根据至少有个整数解求出的取值范围,再解分式方程,根据解是非负整数,可求出满足条件的的值,进一步求解即可.
本题考查了分式方程与一元一次不等式组的综合,熟练掌握解一元一次不等式组和分式方程的解法是解题的关键.
18.【答案】
【解析】解:由题意可得,
解得,
这个数为,
由题意可得,,
整理,可得,
一个“递减数”的前三个数字组成的三位数与后三个数字组成的三位数的和为:
,
又一个“递减数”的前三个数字组成的三位数与后三个数字组成的三位数的和能被整除,
是整数,且,,,,,
时,原四位数可得最大值,此时只能取,不符合题意,舍去,
当时,,此时,
取或或时,均不符合题意,
当取时,,
满足条件的数的最大值是,
故答案为:;.
根据递减数的概念列方程求的值,根据递减数的概念先求得,然后根据题意列出两个三位数字之和,结合能被整除的数的特征分析满足条件的最大值.
本题考查新定义运算,理解新定义概念,正确推理计算是解题关键.
19.【答案】解:原式
.
【解析】根据绝对值性质、零指数幂、负整数指数幂运算法则运算即可.
本题考查了实数的运算,熟练掌握相关运算法则是解答本题的关键.
20.【答案】解:原式
,
当时,
原式
.
【解析】直接利用分式的混合运算法则化简,再把已知数据代入得出答案.
此题主要考查了分式的化简求值,正确化简分式是解题关键.
21.【答案】解:如图,即为所求.
,,.
≌,
,.
点在轴上,
点的位置如图所示.
点的坐标为.
【解析】根据轴对称的性质作图,即可得出答案.
根据全等三角形的判定可确定点的位置,即可得出答案.
本题考查作图轴对称变换、全等三角形的判定,熟练掌握轴对称的性质、全等三角形的判定是解答本题的关键.
22.【答案】解:如图,作线段的垂直平分线,交于点,
为等腰三角形,
,
则即为所求.
为底边上的高,
,
,
,
为等腰三角形,
.
【解析】结合等腰三角形的性质,作线段的垂直平分线,交于点,则即为所求.
由题意可得,进而可得,结合等腰三角形的性质可得.
本题考查作图基本作图、等腰三角形的性质,熟练掌握等腰三角形的性质是解答本题的关键.
23.【答案】
【解析】解:第行第个数是,
故答案为:;
第一行数的和为,
第二行数的和为,
第三行数的和为,
第四行数的和为,
第五行数的和为,
,
第行数的和为.
前行所有的数字之和为;
由题意得,,,,
,
,
,
.
根据从第三行起,每行两端的数都是“”,其余各数都等于该数“两肩”上的数之和即可解决问题;
观察图形的变化得到第行数的和为,即可解决问题;
根据题意得到,,,,于是得到,求得,于是得到结论.
本题考查了规律型:图形的变化规律,解题关键是观察图形的变化发现数字规律.
24.【答案】解:设名工人每小时分拣件包裹,则这条自动分拣流水线每小时分拣件包裹,
依题意,得,
解得:,
检验:当时,,
所以原分式方程的解是,
这条自动分拣流水线每小时分拣包裹:件,
答:一条自动分拣流水线每小时能分拣件包裹;
解:设购买该型号的自动分拣流水线条,
依题意得,
解得:
答:至少应购买条自动分拣流水线.
【解析】设名工人每小时分拣件包裹,则这条自动分拣流水线每小时分拣件包裹,由用一条自动分拣流水线分拣比名工人分拣少用小时.列出方程,可求解;
设购买该型号的自动分拣流水线条,由某转运中心预计每日需分拣的包裹量高达件,列出不等式,即可求解.
本题考查了分式方程的应用,一元一次不等式的应用,找到正确的数量关系是解题的关键.
25.【答案】证明:与都是等边三角形,
,,,
,
在和中,
,
≌,
.
证明:点,分别是,的中点,
,,
,
,
≌,
,
在和中,
,
≌,
,,
,
是等边三角形.
解:与都是等腰直角三角形,
,,,
,
在和中,
,
≌,
,,
点,分别是,的中点,
,,
,
在和中,
,
≌,
,,
,
,且点也是的中点,
,
,
,,
,
,
的面积为.
【解析】由等边三角形的性质得,,,可推导出,进而证明≌,得;
由,,且,证明,而,,可证明≌,得,,可推导出,则是等边三角形;
由等腰直角三角形的性质得,,,可推导出,进而证明≌,得,,而,,所以,可证明≌,得,,推导出,因为,点是的中点,所以,则,所以,.
此题重点考查等边三角形的判定与性质、等腰直角三角形的判定与性质、线段中点的定义、全等三角形的判定与性质、三角形的面积公式等知识,此题综合性强,难度较大,证明≌是解题的关键.
26.【答案】
【解析】解:由关于轴对称的点的特征可知,点关于轴对称点的坐标为;
过点作轴,交直线于点,连接,
点,点关于直线对称,
,,
在和中,
,
≌,
,,
点的坐标为,
,
轴,,
,
点坐标为,
点,
,
,轴,
轴,
,,
点的坐标为;
过点作轴,交直线于点,
点,点关于直线对称,
,,
轴,
,
在和中,
,
≌,
,
轴,点纵坐标为,
点纵坐标为,
直线上任意一点的横坐标与纵坐标的比都是:,
点横坐标为,
,
点横坐标为,
得点的坐标为.
由关于轴对称的点的特征求出对称点的坐标;
过点作轴,交直线于点,连接,通过证明≌,求出的长度,从而得到点的坐标;
过点作轴,交直线于点,证明≌,通过直线上任意一点的横坐标与纵坐标的比都是:求出点的坐标,进而得到点的坐标.
本题考查了关于轴对称的点的特征,平面直角坐标系中的点的坐标,全等三角形的性质与判定,平行线的性质,解题关键在于构造全等三角形,求出相应线段的长度从而得到点的坐标.
第1页,共1页
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.代数式的意义可以是( )
A. 与的和 B. 与的差 C. 与的积 D. 与的商
2.下面四个化学仪器示意图中,是轴对称图形的是( )
A. B. C. D.
3.光年是天文学上的一种距离单位,一光年是指光在一年内走过的路程,约等于,下列正确的是( )
A. B.
C. 是一个位数 D. 是一个位数
4.下列长度的三条线段,能组成三角形的是( )
A. ,, B. ,, C. ,, D. ,,
5.化简的结果是( )
A. B. C. D.
6.若是一个完全平方式,则的值是( )
A. B. C. 或 D. 或
7.如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点,点为焦点若,,则的度数为( )
A. B. C. D.
8.如图,在中,,,的平分线交于,于点,若,则( )
A.
B.
C.
D.
9.千里江山图是宋代王希孟的作品,如图,它的局部画面装裱前是一个长为米,宽为米的矩形,装裱后,整幅图画宽与长的比是:,且四周边衬的宽度相等,则边衬的宽度应是多少米?设边衬的宽度为米,根据题意可列方程( )
A. B. C. D.
10.如图,将两块相同的三角板含角按图中所示位置摆放,若交于,交于,交于,则下列结论中错误的是( )
A. B.
C. ≌ D.
11.若为任意整数,则的值总能( )
A. 被整除 B. 被整除 C. 被整除 D. 被整除
12.在多项式其中中,对相邻的两个字母间任意添加绝对值符号,添加绝对值符号后仍只有减法运算,然后进行去绝对值运算,称此为“绝对操作”例如:,,下列说法:
存在“绝对操作”,使其运算结果与原多项式相等;
不存在“绝对操作”,使其运算结果与原多项式之和为;
所有的“绝对操作”共有种不同运算结果.
其中正确的个数是( )
A. B. C. D.
二、填空题:本题共6小题,每小题2分,共12分。
13.使得分式有意义的条件是______.
14.一个多边形外角和是内角和的,则这个多边形的边数为______.
15.如图,在中,,,点为上一点,连接过点作于点,过点作交的延长线于点若,,则的长度为______.
16.已知,且,则的值为______.
17.若关于的一元一次不等式组至少有个整数解,且关于的分式方程有非负整数解,则所有满足条件的整数的值之和是______.
18.如果一个四位自然数的各数位上的数字互不相等且均不为,满足,那么称这个四位数为“递减数”例如:四位数,,是“递减数”;又如:四位数,,不是“递减数”若一个“递减数”为,则这个数为;若一个“递减数”的前三个数字组成的三位数与后三个数字组成的三位数的和能被整除,则满足条件的数的最大值是______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:.
20.本小题分
先化简,再求值:,其中.
21.本小题分
如图,已知的三个顶点的坐标分别是,,.
画出与关于轴对称的,并直接写出,,的坐标;
在轴上有一点,使得≌,请直接写出点的坐标.
22.本小题分
如图,在等腰中,.
尺规作图:作底边上的高保留作图痕迹,不写作法,并标明字母
在的条件下,若,求的度数.
23.本小题分
“杨辉三角”是中国古代数学重要的成就之一,最早出现在南宋数学家杨辉所著的详解九章算法中其规律是:从第三行起,每行两端的数都是“”,其余各数都等于该数“两肩”上的数之和,如图.
求图中第行第个数是______;
求图中前行所有的数字之和;
“杨辉三角”的应用很广泛,例如“堆垛术”,图中的立体图形是由若干形状、大小相同的圆球摆放而成,从上至下每层小球的个数依次为:,,,,记第层的圆球数记,求的值.
24.本小题分
科技改变世界,为提高快递包裹分拣效率,物流公司引进了快递自动分拣流水线,一条某型号的自动分拣流水线每小时分拣的包裹量是名工人每小时分拣包裹量的倍,分拣件包裹,用一条自动分拣流水线分拣比名工人分拣少用小时.
一条自动分拣流水线每小时能分拣多少件包裹?
新年将至,某转运中心预计每日需分拣的包裹量高达件,现准备购买该型号的自动分拣流水线进行小时作业,则至少应购买多少条?
25.本小题分
【问题情境】如图,与都是等边三角形,连接,,点,分别是,的中点,连接,,.
【猜想证明】请证明:
求证:;
求证:是等边三角形.
【类比探究】如图,与都是等腰直角三角形,连接,,点,分别是,的中点,连接,请探究:
若点恰好也是的中点,且,求的面积.
26.本小题分
综合与实践
【思考尝试】
数学活动课上,老师出示了一个问题:在平面直角坐标系中,点关于轴的对称点的坐标为______;
【实践探究】
小睿受此问题启发,一般化思考并提出新的问题:如图,在平面直角坐标系中,点的坐标为,求点关于直线的对称点的坐标用含,的式子表示;
【拓展迁移】
小博深入研究小睿提出的这个问题,提出新的探究点,并进行了探究:如图,在平面直角坐标系中,点的坐标为,直接写出点关于直线的对称点的坐标用含的式子表示小博经过探究得出直线上任意一点的横坐标与纵坐标的比都是:,点的纵坐标为,请帮助小博完成问题.
答案和解析
1.【答案】
【解析】解:代数式的意义可以是与的积.
故选:.
直接利用代数式的意义分析得出答案.
此题主要考查了代数式,掌握代数式是由运算符号加、减、乘、除、乘方、开方把数或表示数的字母连接而成的式子是解题关键.
2.【答案】
【解析】【试题解析】
解:、不是轴对称图形,故本选项不合题意;
B、不是轴对称图形,故本选项不合题意;
C、不是轴对称图形,故本选项不合题意;
D、是轴对称图形,故本选项符合题意.
故选:.
根据轴对称图形的概念对各选项分析判断即可得解.
本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
3.【答案】
【解析】解:是一个位数.
故选:.
科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正数;当原数的绝对值时,是负数.
此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.
4.【答案】
【解析】解:,,,不能组成三角形,故A选项不符合题意;
,,,不能组成三角形,故B不符合题意;
,,,能组成三角形,故C符合题意;
,,,不能组成三角形,故D不符合题意,
故选:.
根据三角形的三边关系分别判断即可.
本题考查了三角形的三边关系,熟练掌握三角形的三边关系是解题的关键.
5.【答案】
【解析】解:
,
故选:.
先根据分式的乘方法则计算,再根据分式的乘法法则计算.
本题考查的是分式的乘除法,掌握分式的乘法法则、乘方法则是解题的关键.
6.【答案】
【解析】解:是一个完全平方式,
或,
,
或.
故选:.
利用完全平方公式得到或,从而得到,然后解关于的方程.
本题考查了完全平方式:对于一个具有若干个简单变元的整式,如果存在另一个实系数整式,使,则称是完全平方式,即.
7.【答案】
【解析】解:,
,
,
,
,
.
故选:.
由平行线的性质求出,由对顶角的性质得到,由三角形外角的性质即可求出的度数.
本题考查平行线的性质,三角形外角的性质,对顶角的性质,关键是由平行线的性质求出的度数,由对顶角的性质得到的度数,由三角形外角的性质即可解决问题.
8.【答案】
【解析】解:是的平分线,,,
;
,,
,
是的平分线,
,
,
又,
,
是等腰三角形,
,
.
故选:.
首先根据角平分线的性质,可得;然后判断出是等腰三角形,求出的长度,进而求出的长度是多少即可.
此题主要考查了角平分线的性质和应用,以及含度角的直角三角形的性质和应用,要熟练掌握.
9.【答案】
【解析】【解答】
解:由题意可得,
,
故选:.
【分析】
根据题意可知,装裱后的长为,宽为,再根据整幅图画宽与长的比是:,即可得到相应的方程.
本题考查由实际问题抽象出分式方程,解答本题的关键是明确题意,列出相应的分式方程.
10.【答案】
【解析】解:≌,
,,,
,故A正确;
在与中
≌,故C正确;
,故D正确;
故选:.
根据全等三角形的判定和性质判断即可.
此题考查了全等三角形的判定和性质,解题的关键是综合利用全等三角形的判定和性质进行解答.
11.【答案】
【解析】【分析】
先根据完全平方公式进行计算,再合并同类项,分解因式后再逐个判断即可.
本题考查了因式分解的应用,能求出是解此题的关键.
【解答】
解:
,
为任意整数,
的值总能被整除,
故选:.
12.【答案】
【解析】【分析】
根据给定的定义,举出符合条件的说法和说法需要对绝对操作分析添加一个和两个绝对值的情况,并将结果进行比较排除相等的结果,汇总得出答案.
本题考查新定义题型,根据所给的定义,举出符合条件的代数式进行情况讨论;
需要注意去绝对值时的符号,和所有结果可能的比较.主要考查绝对值计算和分类讨论思想的应用.
【解答】
解:,故说法正确.
若使其运算结果与原多项式之和为,需出现,
显然无论怎么添加绝对值,都无法使的符号为负号,故说法正确.
当添加一个绝对值时,共有种情况,分别是;;;当添加两个绝对值时,共有种情况,分别是;;共有种情况;
有两对运算结果相同,故共有种不同运算结果,故说法错误.
综上,说法正确的有共个.
故选:.
13.【答案】
【解析】解:由题意得:,
解得:,
故答案为:.
根据分式有意义的条件可得:,再解即可.
此题主要考查了分式有意义的条件,关键是掌握分式有意义的条件是分母不等于零.
14.【答案】
【解析】解:根据题意可得:,
解得:,
故答案为:.
多边形的内角和定理为,多边形的外角和为,根据题意列出方程求出的值.
本题主要考查的是多边形的内角和公式以及外角和定理,属于基础题型.记忆理解并应用这两个公式是解题的关键.
15.【答案】
【解析】解:,,
,
,
,
,
,
在和中,
,
≌,
,,
,,
,,
,
故答案为:.
先证明≌,根据全等三角形的性质可得,,进一步可得的长.
本题考查了全等三角形的判定和性质,等腰直角三角形的性质,熟练掌握全等三角形的判定方法是解题的关键.
16.【答案】
【解析】解:,
,
,
.
故答案为:.
根据,可得,再代入即可求出答案.
本题考查了分式的加减法和分式的值,熟练掌握分式的运算法则是关键.
17.【答案】
【解析】解:解不等式组,得,
至少有个整数解,
,
,
解分式方程,
得,
的值是非负整数,,
当时,,
当时,,
当时,,
是分式方程的增根,
舍去,
满足条件的的值有和,
,
所有满足条件的整数的值之和是.
故答案为:.
先解不等式组,根据至少有个整数解求出的取值范围,再解分式方程,根据解是非负整数,可求出满足条件的的值,进一步求解即可.
本题考查了分式方程与一元一次不等式组的综合,熟练掌握解一元一次不等式组和分式方程的解法是解题的关键.
18.【答案】
【解析】解:由题意可得,
解得,
这个数为,
由题意可得,,
整理,可得,
一个“递减数”的前三个数字组成的三位数与后三个数字组成的三位数的和为:
,
又一个“递减数”的前三个数字组成的三位数与后三个数字组成的三位数的和能被整除,
是整数,且,,,,,
时,原四位数可得最大值,此时只能取,不符合题意,舍去,
当时,,此时,
取或或时,均不符合题意,
当取时,,
满足条件的数的最大值是,
故答案为:;.
根据递减数的概念列方程求的值,根据递减数的概念先求得,然后根据题意列出两个三位数字之和,结合能被整除的数的特征分析满足条件的最大值.
本题考查新定义运算,理解新定义概念,正确推理计算是解题关键.
19.【答案】解:原式
.
【解析】根据绝对值性质、零指数幂、负整数指数幂运算法则运算即可.
本题考查了实数的运算,熟练掌握相关运算法则是解答本题的关键.
20.【答案】解:原式
,
当时,
原式
.
【解析】直接利用分式的混合运算法则化简,再把已知数据代入得出答案.
此题主要考查了分式的化简求值,正确化简分式是解题关键.
21.【答案】解:如图,即为所求.
,,.
≌,
,.
点在轴上,
点的位置如图所示.
点的坐标为.
【解析】根据轴对称的性质作图,即可得出答案.
根据全等三角形的判定可确定点的位置,即可得出答案.
本题考查作图轴对称变换、全等三角形的判定,熟练掌握轴对称的性质、全等三角形的判定是解答本题的关键.
22.【答案】解:如图,作线段的垂直平分线,交于点,
为等腰三角形,
,
则即为所求.
为底边上的高,
,
,
,
为等腰三角形,
.
【解析】结合等腰三角形的性质,作线段的垂直平分线,交于点,则即为所求.
由题意可得,进而可得,结合等腰三角形的性质可得.
本题考查作图基本作图、等腰三角形的性质,熟练掌握等腰三角形的性质是解答本题的关键.
23.【答案】
【解析】解:第行第个数是,
故答案为:;
第一行数的和为,
第二行数的和为,
第三行数的和为,
第四行数的和为,
第五行数的和为,
,
第行数的和为.
前行所有的数字之和为;
由题意得,,,,
,
,
,
.
根据从第三行起,每行两端的数都是“”,其余各数都等于该数“两肩”上的数之和即可解决问题;
观察图形的变化得到第行数的和为,即可解决问题;
根据题意得到,,,,于是得到,求得,于是得到结论.
本题考查了规律型:图形的变化规律,解题关键是观察图形的变化发现数字规律.
24.【答案】解:设名工人每小时分拣件包裹,则这条自动分拣流水线每小时分拣件包裹,
依题意,得,
解得:,
检验:当时,,
所以原分式方程的解是,
这条自动分拣流水线每小时分拣包裹:件,
答:一条自动分拣流水线每小时能分拣件包裹;
解:设购买该型号的自动分拣流水线条,
依题意得,
解得:
答:至少应购买条自动分拣流水线.
【解析】设名工人每小时分拣件包裹,则这条自动分拣流水线每小时分拣件包裹,由用一条自动分拣流水线分拣比名工人分拣少用小时.列出方程,可求解;
设购买该型号的自动分拣流水线条,由某转运中心预计每日需分拣的包裹量高达件,列出不等式,即可求解.
本题考查了分式方程的应用,一元一次不等式的应用,找到正确的数量关系是解题的关键.
25.【答案】证明:与都是等边三角形,
,,,
,
在和中,
,
≌,
.
证明:点,分别是,的中点,
,,
,
,
≌,
,
在和中,
,
≌,
,,
,
是等边三角形.
解:与都是等腰直角三角形,
,,,
,
在和中,
,
≌,
,,
点,分别是,的中点,
,,
,
在和中,
,
≌,
,,
,
,且点也是的中点,
,
,
,,
,
,
的面积为.
【解析】由等边三角形的性质得,,,可推导出,进而证明≌,得;
由,,且,证明,而,,可证明≌,得,,可推导出,则是等边三角形;
由等腰直角三角形的性质得,,,可推导出,进而证明≌,得,,而,,所以,可证明≌,得,,推导出,因为,点是的中点,所以,则,所以,.
此题重点考查等边三角形的判定与性质、等腰直角三角形的判定与性质、线段中点的定义、全等三角形的判定与性质、三角形的面积公式等知识,此题综合性强,难度较大,证明≌是解题的关键.
26.【答案】
【解析】解:由关于轴对称的点的特征可知,点关于轴对称点的坐标为;
过点作轴,交直线于点,连接,
点,点关于直线对称,
,,
在和中,
,
≌,
,,
点的坐标为,
,
轴,,
,
点坐标为,
点,
,
,轴,
轴,
,,
点的坐标为;
过点作轴,交直线于点,
点,点关于直线对称,
,,
轴,
,
在和中,
,
≌,
,
轴,点纵坐标为,
点纵坐标为,
直线上任意一点的横坐标与纵坐标的比都是:,
点横坐标为,
,
点横坐标为,
得点的坐标为.
由关于轴对称的点的特征求出对称点的坐标;
过点作轴,交直线于点,连接,通过证明≌,求出的长度,从而得到点的坐标;
过点作轴,交直线于点,证明≌,通过直线上任意一点的横坐标与纵坐标的比都是:求出点的坐标,进而得到点的坐标.
本题考查了关于轴对称的点的特征,平面直角坐标系中的点的坐标,全等三角形的性质与判定,平行线的性质,解题关键在于构造全等三角形,求出相应线段的长度从而得到点的坐标.
第1页,共1页
同课章节目录
