1.2.2函数的表示法
图片预览






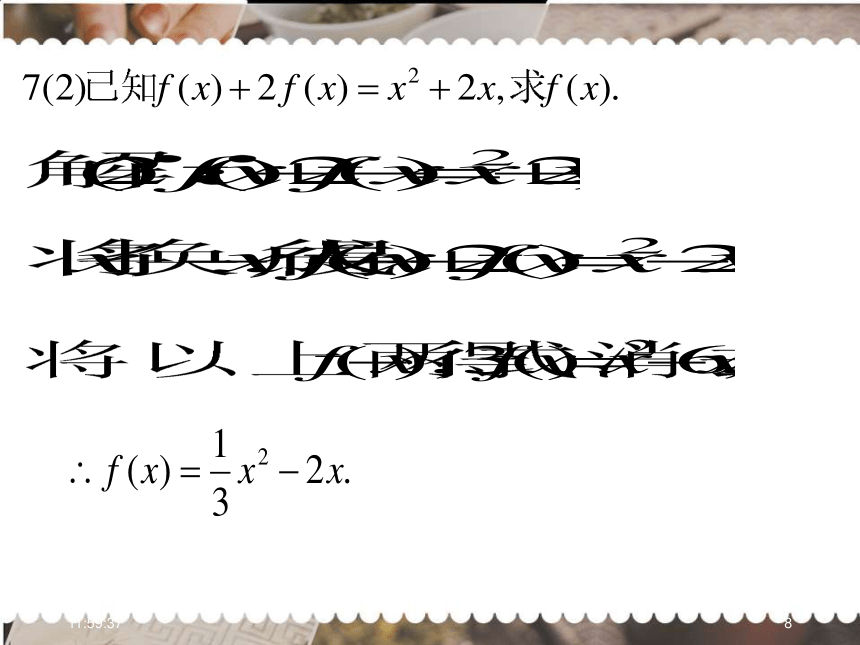



文档简介
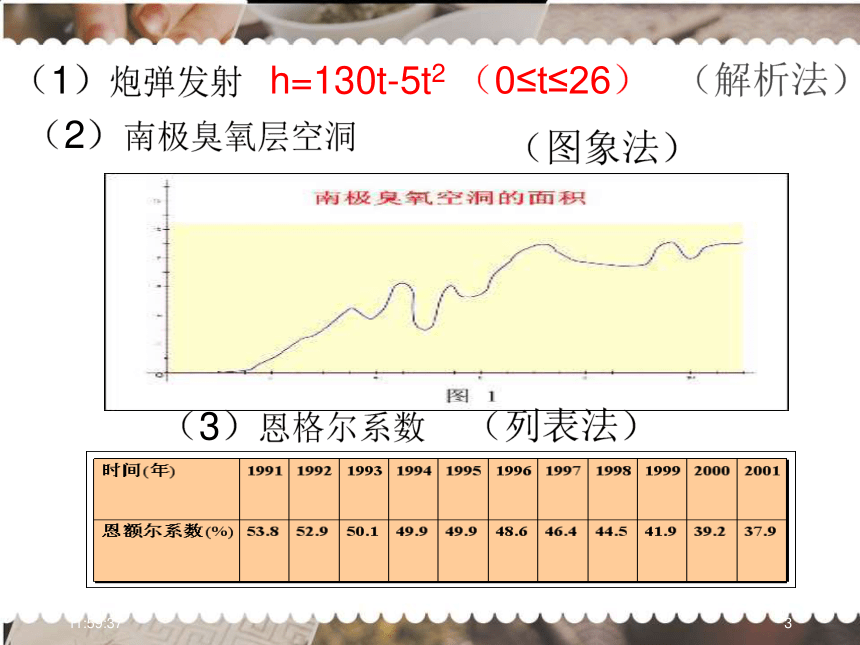
课件42张PPT。1.2.2 函数的表示法17:10:511初中学过哪些函数的表示方法?问题课本1.2.1节的三个实例分别用了哪些表示方法?其各自的优点是什么?17:10:511(1)炮弹发射(解析法)h=130t-5t2 (0≤t≤26)(2)南极臭氧层空洞(图象法)(3)恩格尔系数(列表法)17:10:511 把两个变量的关系, 用一个等式
表示, 这个等式就叫做函数的解析式. 优点: 函数关系清楚, 便于研究 函数性质.1. 解析法:17:10:5114.已知f(x)是一次函数,2f(2)-3f(1)=5,2f(0)-f(-1)=1,则( )
A.f(x)=3x+2 B.f(x)=3x-2
C.f(x)=2x+3 D.f(x)=2x-3B17:10:511【例3】 求下列函数的解析式:
(1)已知f(x)为一次函数且f[f(x)]=4x-1,求f(x);解:(1)(待定系数法)∵f(x)是一次函数.设f(x)=kx+b(k≠0).则f[f(x)]=f(kx+b)=k(kx+b)+b=k2x+kb+b=4x-1,17:10:5115.已知f(2x+1)=3x-2且f(a)=4,则a的值为______.517:10:51117:10:511优点:直观形象. 2. 图象法:如:一次函数的图象是一条直线;
如函数 y=kx+b (k<0、b>0) 用函数图象来表示两个变量之
间的关系.17:10:521【例2】 作出下列函数图象:
(1)y=1-x(x∈Z且|x|≤2);
(2)y=2x2-4x-3(0≤x<3).解:(1)∵x∈Z且|x|≤2,
∴x∈{-2,-1,0,1,2}.
∴图象为一直线上的孤立点[如图(1)].(2)∵y=2(x-1)2-5,
∴当x=0时,y=-3;
当x=3时,y=3;
当x=1时,y=-5.
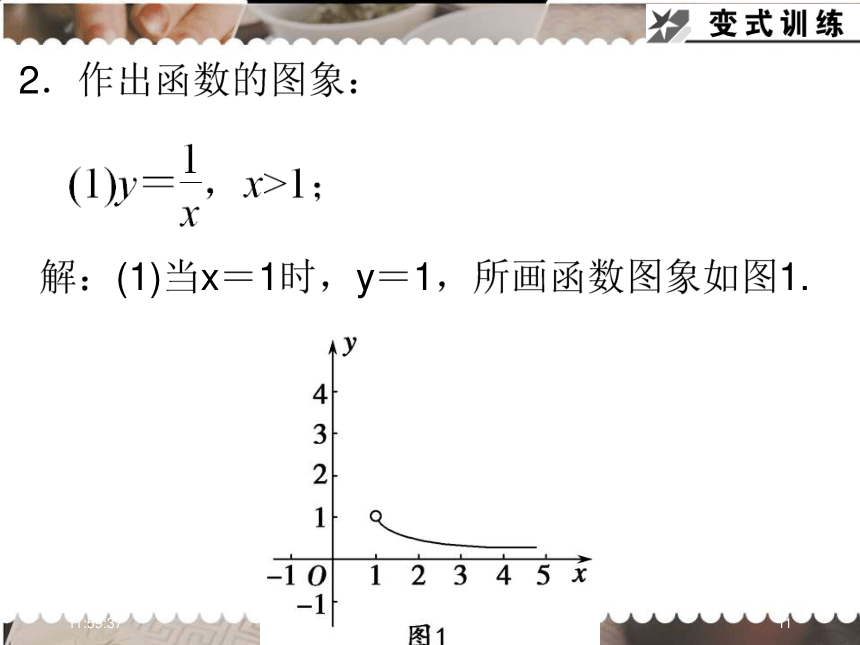
所画函数图象如图(2).17:10:5212.作出函数的图象:解:(1)当x=1时,y=1,所画函数图象如图1.17:10:5213. 列表法:优点: 易知自变量与函数的对应性.列出表格来表示两个变量的关系.如:平方表,平方根表,汽车、
火车站的里程价目表、银行里的
“利率表”等等. 17:10:5216.已知f(x)与g(x)分别由下表给出,那么f(g(3))=___.117:10:521解:这个函数的定义域是数集{1,2,3,4,5}
用解析法可将函数y=f(x)表示为用列表法可将函数表示为17:10:521用图象法可将函数表示为下图.....17:10:521(1)用解析法表示函数是否一定要写出自变量的取值范围?(2)用描点法画函数图象的一般步骤是什么?本题中的图象为什么不是一条直线? 写函数解析式的时候,要写出函数的定义域。列表、描点、连线(视其定义域决定是否连线)函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等。17:10:521 如图,把截面半径为25cm的圆形木头锯成矩形木料,如果矩形的一边长为xcm,面积为ycm2,把y表示为x的函数.ABCD针对练习(课本23页 1)17:10:521 例4. 下表是某校高一(1)班三名同学在高一学年六次数学测试的成绩及班级平均分表. 请你对这三位同学在高一学年度的数学学习情况做一个分析.17:10:521 分析:从表中可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况.如果将“成绩”与“测试时间”之间的关系用函数图象表示出来,那么就能比较直观地看到成绩变化的情况.17:10:521王伟张城赵磊班平均分17:10:521赵磊同学的数学学习成绩低于班级平均水平,但他的成绩曲线呈上升趋势,表明他的数学成绩稳步提高.王伟同学的数学成绩始终高于班级平均分,学习情况比较稳定而且成绩优秀.张城同学的数学成绩不稳定,总是在班级平均分水平上下波动,而且波动幅度较大.一、函数的三种表示法17:10:521 下图中哪几个图象与下述三件事分别吻合得最好?请你为剩下的那个图象写出一件事.
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
(2)我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(A) (B) (C) (D)DAB针对练习(课本23页 2)17:10:531例5. 画出函数y=|x|的图象.17:10:531 例6. 某市“招手即停”公共汽车的票价按下列规则指定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).
如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象.17:10:531解:设票价为y,里程为x,则根据题意,
如果某空调汽车运行路线中设21个汽车站,那么汽车行驶的里程约为20公里,所以自变量x的取值范围是(0,20]由空调汽车票价的规定,可得到以下函数解析式:y=2, 03, 5 < x ≤ 10
4, 10 < x ≤ 15
5, 15 < x≤2017:10:531有些函数在它的定义域中,对于自变量的不同取值范围,对应关系不同,这种函数通常称为分段函数。17:10:531分段函数 所谓“分段函数”,习惯上指在定义域的不同部分,有不同的对应法则的函数,对它应有以下两点基本认识:
(1)分段函数是一个函数,不要把它误认为是几个函数;
(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集。17:10:531【例2】 (1)已知函数则f(f(1))=________;3A17:10:531C17:10:5312.下列图形是函数y=x|x|的图像的是( )D17:10:531【例1】 已知函数(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;(3)写出该函数的值域.解:(1)当0≤x≤2时,当-2(2)画出该函数的图象;(3)写出该函数的值域.(2)函数f(x)的图象如右图所示.
(3)由(2),知f(x)在(-2,2]上的值域为[1,3).17:10:531①开平方③求正弦 ④乘以2 1
-1
2
-2
3
-31
4
9②求平方 观察下列对应:17:10:531映射 一般地,我们有:
设A,B是两个非空集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合B中都有惟一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射(mapping),记作
f:A→B .
其中x叫做原象(inverse image),与x对应的y叫做象(image).17:10:531 若f是从集合A到B的映射,如果对集合A中的不同元素在集合B中都有不同的象,并且B中每一个元素在A中都有原象,这样的映射叫做从集合A到集合B的一一映射.一一映射的定义:17:10:531一种对应是映射,必须满足两个条件: ①A中任何一个元素在B中都有元素与之
对应(至于B中元素是否在A中有元素对应
不必考虑,即B中可有“多余”元素).
②B中所对应的元素是唯一的 (即“一对
多”不是映射,而“多对一”可构成映
射,如图(1)中对应不是映射).理 解:17:10:531函数是一个特殊的映射;
2)函数是非空数集A到非空数集B的映射,
而对于映射,A和B不一定是数集.你能说出函数与映射之间的异同吗?思 考:17:10:531 例7. 以下给出的对应是不是从集合A到B的映射?
(1)集合A={P|P是数轴上的点},集合B=R,对应关系f:数轴上的点与它所代表的实数对应;17:10:531
(2)集合A={P|P是平面直角坐标系中的点},集合B={(x,y)|x∈R,y∈R},对应关系f:平面直角坐标系中的点与它的坐标对应;17:10:531
(3)集合A={x|x是三角形},集合B={x|x是圆},对应关系f:每一个三角形都对应它的内切圆;17:10:541
(4)集合A={x|x是新华中学的班级},集合B={x|x是新华中学的学生},对应关系f:每一个班级都对应班里的学生.17:10:541C17:10:541
表示, 这个等式就叫做函数的解析式. 优点: 函数关系清楚, 便于研究 函数性质.1. 解析法:17:10:5114.已知f(x)是一次函数,2f(2)-3f(1)=5,2f(0)-f(-1)=1,则( )
A.f(x)=3x+2 B.f(x)=3x-2
C.f(x)=2x+3 D.f(x)=2x-3B17:10:511【例3】 求下列函数的解析式:
(1)已知f(x)为一次函数且f[f(x)]=4x-1,求f(x);解:(1)(待定系数法)∵f(x)是一次函数.设f(x)=kx+b(k≠0).则f[f(x)]=f(kx+b)=k(kx+b)+b=k2x+kb+b=4x-1,17:10:5115.已知f(2x+1)=3x-2且f(a)=4,则a的值为______.517:10:51117:10:511优点:直观形象. 2. 图象法:如:一次函数的图象是一条直线;
如函数 y=kx+b (k<0、b>0) 用函数图象来表示两个变量之
间的关系.17:10:521【例2】 作出下列函数图象:
(1)y=1-x(x∈Z且|x|≤2);
(2)y=2x2-4x-3(0≤x<3).解:(1)∵x∈Z且|x|≤2,
∴x∈{-2,-1,0,1,2}.
∴图象为一直线上的孤立点[如图(1)].(2)∵y=2(x-1)2-5,
∴当x=0时,y=-3;
当x=3时,y=3;
当x=1时,y=-5.
所画函数图象如图(2).17:10:5212.作出函数的图象:解:(1)当x=1时,y=1,所画函数图象如图1.17:10:5213. 列表法:优点: 易知自变量与函数的对应性.列出表格来表示两个变量的关系.如:平方表,平方根表,汽车、
火车站的里程价目表、银行里的
“利率表”等等. 17:10:5216.已知f(x)与g(x)分别由下表给出,那么f(g(3))=___.117:10:521解:这个函数的定义域是数集{1,2,3,4,5}
用解析法可将函数y=f(x)表示为用列表法可将函数表示为17:10:521用图象法可将函数表示为下图.....17:10:521(1)用解析法表示函数是否一定要写出自变量的取值范围?(2)用描点法画函数图象的一般步骤是什么?本题中的图象为什么不是一条直线? 写函数解析式的时候,要写出函数的定义域。列表、描点、连线(视其定义域决定是否连线)函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等。17:10:521 如图,把截面半径为25cm的圆形木头锯成矩形木料,如果矩形的一边长为xcm,面积为ycm2,把y表示为x的函数.ABCD针对练习(课本23页 1)17:10:521 例4. 下表是某校高一(1)班三名同学在高一学年六次数学测试的成绩及班级平均分表. 请你对这三位同学在高一学年度的数学学习情况做一个分析.17:10:521 分析:从表中可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况.如果将“成绩”与“测试时间”之间的关系用函数图象表示出来,那么就能比较直观地看到成绩变化的情况.17:10:521王伟张城赵磊班平均分17:10:521赵磊同学的数学学习成绩低于班级平均水平,但他的成绩曲线呈上升趋势,表明他的数学成绩稳步提高.王伟同学的数学成绩始终高于班级平均分,学习情况比较稳定而且成绩优秀.张城同学的数学成绩不稳定,总是在班级平均分水平上下波动,而且波动幅度较大.一、函数的三种表示法17:10:521 下图中哪几个图象与下述三件事分别吻合得最好?请你为剩下的那个图象写出一件事.
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
(2)我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(A) (B) (C) (D)DAB针对练习(课本23页 2)17:10:531例5. 画出函数y=|x|的图象.17:10:531 例6. 某市“招手即停”公共汽车的票价按下列规则指定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).
如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象.17:10:531解:设票价为y,里程为x,则根据题意,
如果某空调汽车运行路线中设21个汽车站,那么汽车行驶的里程约为20公里,所以自变量x的取值范围是(0,20]由空调汽车票价的规定,可得到以下函数解析式:y=2, 0
4, 10 < x ≤ 15
5, 15 < x≤2017:10:531有些函数在它的定义域中,对于自变量的不同取值范围,对应关系不同,这种函数通常称为分段函数。17:10:531分段函数 所谓“分段函数”,习惯上指在定义域的不同部分,有不同的对应法则的函数,对它应有以下两点基本认识:
(1)分段函数是一个函数,不要把它误认为是几个函数;
(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集。17:10:531【例2】 (1)已知函数则f(f(1))=________;3A17:10:531C17:10:5312.下列图形是函数y=x|x|的图像的是( )D17:10:531【例1】 已知函数(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;(3)写出该函数的值域.解:(1)当0≤x≤2时,当-2
(3)由(2),知f(x)在(-2,2]上的值域为[1,3).17:10:531①开平方③求正弦 ④乘以2 1
-1
2
-2
3
-31
4
9②求平方 观察下列对应:17:10:531映射 一般地,我们有:
设A,B是两个非空集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合B中都有惟一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射(mapping),记作
f:A→B .
其中x叫做原象(inverse image),与x对应的y叫做象(image).17:10:531 若f是从集合A到B的映射,如果对集合A中的不同元素在集合B中都有不同的象,并且B中每一个元素在A中都有原象,这样的映射叫做从集合A到集合B的一一映射.一一映射的定义:17:10:531一种对应是映射,必须满足两个条件: ①A中任何一个元素在B中都有元素与之
对应(至于B中元素是否在A中有元素对应
不必考虑,即B中可有“多余”元素).
②B中所对应的元素是唯一的 (即“一对
多”不是映射,而“多对一”可构成映
射,如图(1)中对应不是映射).理 解:17:10:531函数是一个特殊的映射;
2)函数是非空数集A到非空数集B的映射,
而对于映射,A和B不一定是数集.你能说出函数与映射之间的异同吗?思 考:17:10:531 例7. 以下给出的对应是不是从集合A到B的映射?
(1)集合A={P|P是数轴上的点},集合B=R,对应关系f:数轴上的点与它所代表的实数对应;17:10:531
(2)集合A={P|P是平面直角坐标系中的点},集合B={(x,y)|x∈R,y∈R},对应关系f:平面直角坐标系中的点与它的坐标对应;17:10:531
(3)集合A={x|x是三角形},集合B={x|x是圆},对应关系f:每一个三角形都对应它的内切圆;17:10:541
(4)集合A={x|x是新华中学的班级},集合B={x|x是新华中学的学生},对应关系f:每一个班级都对应班里的学生.17:10:541C17:10:541
