隐形圆问题梳理及运用 课件(共15张PPT)2024年高考数学复习二轮专题
文档属性
| 名称 | 隐形圆问题梳理及运用 课件(共15张PPT)2024年高考数学复习二轮专题 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 15:31:11 | ||
图片预览





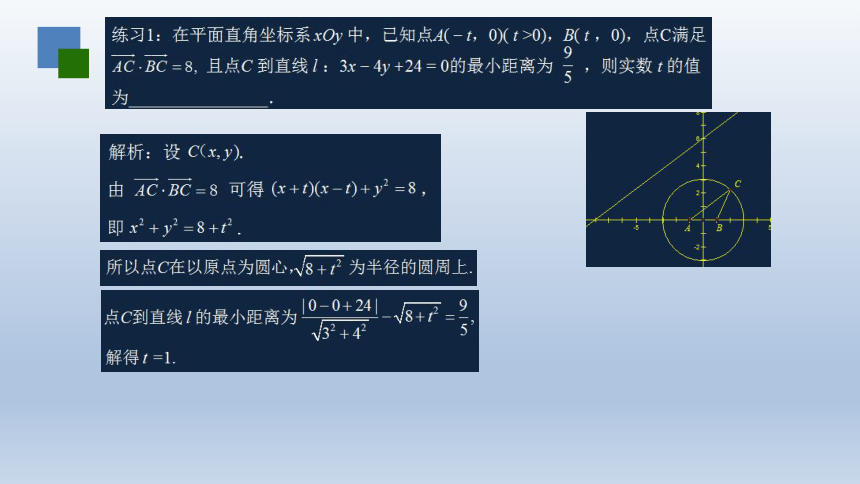
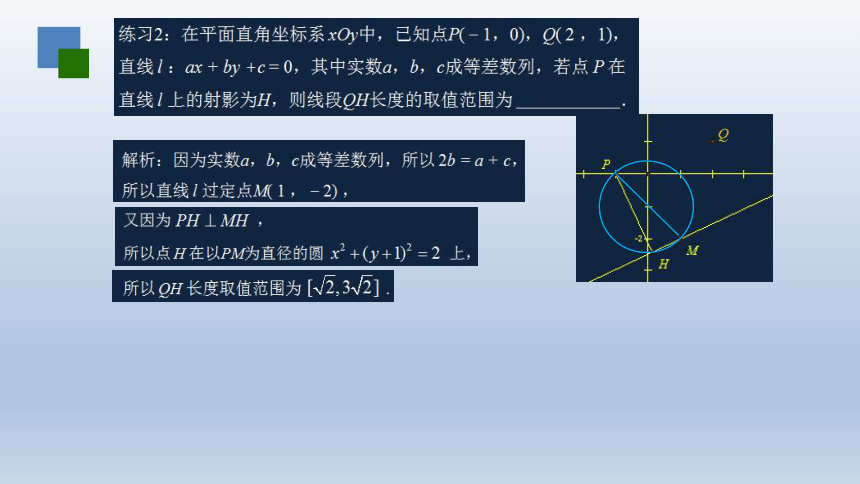
文档简介
(共15张PPT)
隐形圆问题梳理及运用
苏教版高三数学
2024年高考数学复习二轮专题 课件★★
隐圆问题是高考中的一个热点和重点,尤其是阿波罗尼斯圆在高考中频频出现.此类问题涉及知识面广(三角,向量,不等式,解析几何等),处理此类问题的关键是寻找动点满足的条件,得出动点的轨迹是一个定圆,从而把问题转化为点和圆、直线和圆、圆和圆的位置关系问题,并在解决问题的过程中感悟合理转化、化繁为简、数形结合的数学思想方法.
本专题主要来研究发现隐圆并用隐圆解决相关问题.
D
E
A
B
C
注: 中,若AB为定长,则以下关系表明点C在圆上 :
轨迹思想
阿波罗尼斯圆:平面上到两个定点的距离之比为定值(不为1)的点的
轨迹是一个圆。
阿波罗尼斯圆
.
Q
小结:
常见转化途径:
三角形外接圆
轨迹思想求出圆
阿波罗尼斯圆
核心思想: 合理转化 数形结合
作业:
2.已知A(0,1),B(1,0),C(t,0),点D是直线AC上的动点,若AD ≤ 2BD恒成立,
则最小正整数t的值为________________.
1.在三角形ABC 中,角A ,B ,C 所对的边a ,b ,c 满足 2a2+b2+c2=8 ,
求三角形ABC面积的最大值.
的点P有两个,则实数 的取值范围是_______________.
3.已知点A(2,3),点B(6,-3),点P在直线3x - 4y + 3 = 0上,若满足等式
4.在平面直角坐标系 xOy 中,已知B,C为圆 上两点,点A(1,1),
且 ,则线段BC的长的取值范围为_______________.
5.在平面直角坐标系xOy中,已知圆C经过A(0,2),O(0,0),D(t,0) ( t > 0 ) 三点,
M是线段AD上的动点,l1,l2是过点B(1,0)且互相垂直的两条直线,其中l1交y轴
于点E,l2 交圆C于P,Q 两点.
(1)若t =PQ=6,求直线l2的方程;
(2)若t是使 AM ≤ 2BM 恒成立的最小正整数,求三角形EPQ的面积的最小值.
谢谢聆听
隐形圆问题梳理及运用
苏教版高三数学
2024年高考数学复习二轮专题 课件★★
隐圆问题是高考中的一个热点和重点,尤其是阿波罗尼斯圆在高考中频频出现.此类问题涉及知识面广(三角,向量,不等式,解析几何等),处理此类问题的关键是寻找动点满足的条件,得出动点的轨迹是一个定圆,从而把问题转化为点和圆、直线和圆、圆和圆的位置关系问题,并在解决问题的过程中感悟合理转化、化繁为简、数形结合的数学思想方法.
本专题主要来研究发现隐圆并用隐圆解决相关问题.
D
E
A
B
C
注: 中,若AB为定长,则以下关系表明点C在圆上 :
轨迹思想
阿波罗尼斯圆:平面上到两个定点的距离之比为定值(不为1)的点的
轨迹是一个圆。
阿波罗尼斯圆
.
Q
小结:
常见转化途径:
三角形外接圆
轨迹思想求出圆
阿波罗尼斯圆
核心思想: 合理转化 数形结合
作业:
2.已知A(0,1),B(1,0),C(t,0),点D是直线AC上的动点,若AD ≤ 2BD恒成立,
则最小正整数t的值为________________.
1.在三角形ABC 中,角A ,B ,C 所对的边a ,b ,c 满足 2a2+b2+c2=8 ,
求三角形ABC面积的最大值.
的点P有两个,则实数 的取值范围是_______________.
3.已知点A(2,3),点B(6,-3),点P在直线3x - 4y + 3 = 0上,若满足等式
4.在平面直角坐标系 xOy 中,已知B,C为圆 上两点,点A(1,1),
且 ,则线段BC的长的取值范围为_______________.
5.在平面直角坐标系xOy中,已知圆C经过A(0,2),O(0,0),D(t,0) ( t > 0 ) 三点,
M是线段AD上的动点,l1,l2是过点B(1,0)且互相垂直的两条直线,其中l1交y轴
于点E,l2 交圆C于P,Q 两点.
(1)若t =PQ=6,求直线l2的方程;
(2)若t是使 AM ≤ 2BM 恒成立的最小正整数,求三角形EPQ的面积的最小值.
谢谢聆听
同课章节目录
