与几何图形有关的应用题处理策略 课件(共20张PPT)2024年高考数学复习二轮专题
文档属性
| 名称 | 与几何图形有关的应用题处理策略 课件(共20张PPT)2024年高考数学复习二轮专题 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 15:38:10 | ||
图片预览






文档简介
(共20张PPT)
高三 数学
与几何图形有关的应用问题处理策略
2024年高考数学复习二轮专题 课件★★
例题激活
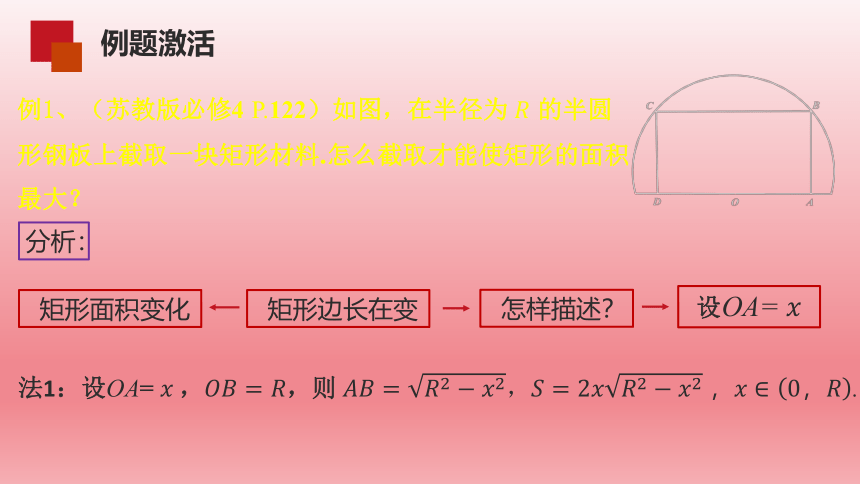
例1、(苏教版必修4 P.122)如图,在半径为 的半圆形钢板上截取一块矩形材料.怎么截取才能使矩形的面积最大?
矩形面积变化
矩形边长在变
怎样描述?
设OA=
分析:
法1:设OA= ,,则 ,
,.
例题激活
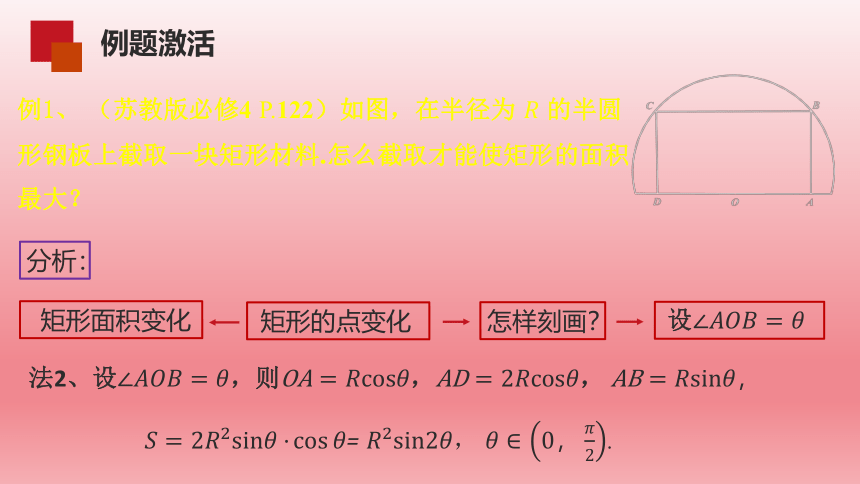
法2、设,则,, ,
= , .
矩形面积变化
矩形的点变化
怎样刻画?
设
分析:
例1、 (苏教版必修4 P.122)如图,在半径为 的半圆形钢板上截取一块矩形材料.怎么截取才能使矩形的面积最大?
例题激活
法3、以O为原点,AD所在直线为轴,建立直角坐标系,设,,点B在第一象限,,其中.
矩形面积变化
矩形的点变化
刻画点B变化
解析法
分析:
y
例1、 (苏教版必修4 P.122)如图,在半径为 的半圆形钢板上截取一块矩形材料.怎么截取才能使矩形的面积最大?
例题激活
①
②
,其中 ③
思考:三个关系式有什么联系?
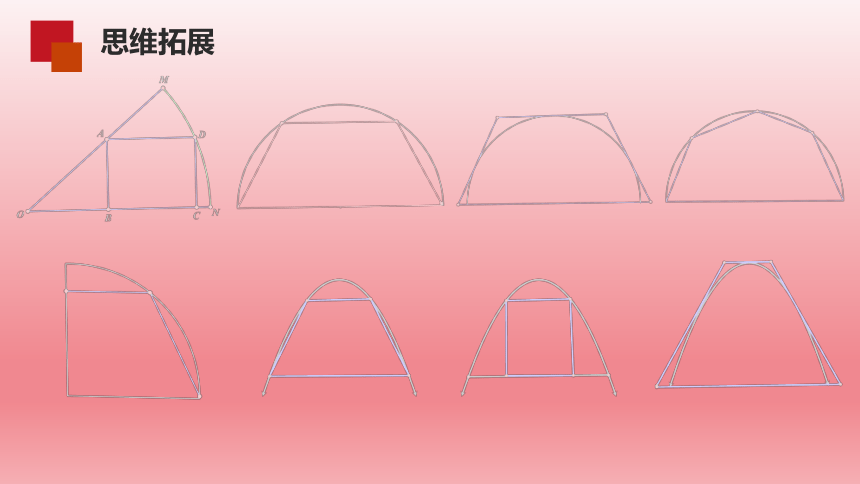
思维拓展
圆
半圆,扇形,弓形,抛物线,三角形,组合图形……
求内接于半径为R的圆的内接矩形面积的最大值.(选修1-1习题)
在半径为的半圆形钢板上截取一块矩形材料,怎么截取才能使矩形的面积最大?(苏教版必修4 习题)
矩形
三角形,梯形,平行四边形,组合图形……
内接
外切,内含……
面积
周长,线段和,线段积,平方和……
平面
立体(球,正方体,长方体,圆柱……)
思维拓展
例2、某农场有一块农田,如图所示,它的边界由圆O的一段圆弧 (M 为此圆弧的中点)和线段EF构成.已知圆O的半径为40米(圆心O在弓形EMF内),现规划在此农田上修建形状为矩形ABCD的温室大棚,其中 AD∥EF,且点A、D 在半圆O上,问如何修建使得矩形ABCD的面积最大?
拓展应用
解:设,(1)当时,点B、C在EF上,此时,
所以
拓展应用
(2)当时,点B、C在圆弧上,此时,,所以
综上,
令的
记区间内余弦值等于的角为(唯一存在),列表得:
拓展应用
+ 0 -
单调递增 极大值 单调递减
又当时,在上的单调减函数,
所以当即时矩形的面积最大.
思维拓展
例3、(2020苏州高三期末18题)为响应“生产发展、生活富裕、乡风文明、村容整洁、管理民主”的社会主义新农村建设,某自然村将村边一块废弃的扇形荒地(如图)租给蜂农养蜂、产蜜与售蜜.已知扇形AOB中,AOB = ,OB= (百米)荒地内规划修建两条直路AB,OC,其中点C在上,(C与A,B不重合),在小路AB与OC的交点D处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区。设,蜂巢区的面积为S(平方百米).
(1)求S关于的函数关系式;
(2)为何值时,蜂巢区的面积S最小,并求此时S的最小值.
思维拓展
思维拓展
思维拓展
例4、(2019年南通二模)如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的半径都是2km,点P在圆Q上,现要在公园内建一块顶点都在圆P上的多边形活动场地.
(1)如图甲,要建的活动场地为△RST,求场地的最大面积;
【解】(1)如右图,过S作SH⊥RT于H,S△RST=
由题意,△RST 在月牙形公园里,RT与圆Q只能相切或相离;
RT左边的部分是一个大小不超过半圆的弓形,则有RT≤4,SH≤2,当且仅当RT切圆Q于P时(如左图),上面两个不等式中等号同时成立.
如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的半径都是2km,点P在圆Q上,现要在公园内建一块顶点都在圆P上的多边形活动场地.(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
思维拓展
解:同(1)的分析,要使得场地面积最大,AD左边的部分是一个大小不超过半圆的弓形,AD必须切圆Q于P,再设.
思维拓展
链接高考
(2018江苏高考)某农场有一块农田,如图所示,它的边界由圆O的一段圆弧 MPN(P为此圆弧的中点)和线段 MN 构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为CPD ,要求A,B 均在线段MN 上,C,D 均在圆弧上.设OC与MN所成的角为.若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3,求当为何值时,能使甲、乙两种蔬菜的年总产值最大.
课堂小结
思考:数学建模的一般过程是什么?
应用题建模四个步骤:“探明关键要素、选择合适参数、探求数学关系、关注变量范围”.
题在书外,根在课本.
课后练习
1、 (2018江苏高考)某农场有一块农田,如图所示,它的边界由圆O的一段圆弧 MPN(P为此圆弧的中点)和线段 MN 构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为CPD ,要求A,B 均在线段MN 上,C,D 均在圆弧上.设OC与MN所成的角为.若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3,求当为何值时,能使甲、乙两种蔬菜的年总产值最大.
课后练习
2、(2019泰州一模)如图,三个小区分别位于扇形OAB的三个顶点上,Q是弧AB的中点,现欲在线段OQ上找一处开挖工作坑P(不与点O,Q重合),为小区铺设三条地下电缆管线PO,PA,PB,已知OA=2千米, ,记∠APQ= θ rad,地下电缆管线的总长度为y千米.
(1) 将y表示成θ的函数,并写出θ的范围;
(2) 请确定工作坑P的位置,使地下电缆管线的总长度最小.
高三 数学
与几何图形有关的应用问题处理策略
2024年高考数学复习二轮专题 课件★★
例题激活
例1、(苏教版必修4 P.122)如图,在半径为 的半圆形钢板上截取一块矩形材料.怎么截取才能使矩形的面积最大?
矩形面积变化
矩形边长在变
怎样描述?
设OA=
分析:
法1:设OA= ,,则 ,
,.
例题激活
法2、设,则,, ,
= , .
矩形面积变化
矩形的点变化
怎样刻画?
设
分析:
例1、 (苏教版必修4 P.122)如图,在半径为 的半圆形钢板上截取一块矩形材料.怎么截取才能使矩形的面积最大?
例题激活
法3、以O为原点,AD所在直线为轴,建立直角坐标系,设,,点B在第一象限,,其中.
矩形面积变化
矩形的点变化
刻画点B变化
解析法
分析:
y
例1、 (苏教版必修4 P.122)如图,在半径为 的半圆形钢板上截取一块矩形材料.怎么截取才能使矩形的面积最大?
例题激活
①
②
,其中 ③
思考:三个关系式有什么联系?
思维拓展
圆
半圆,扇形,弓形,抛物线,三角形,组合图形……
求内接于半径为R的圆的内接矩形面积的最大值.(选修1-1习题)
在半径为的半圆形钢板上截取一块矩形材料,怎么截取才能使矩形的面积最大?(苏教版必修4 习题)
矩形
三角形,梯形,平行四边形,组合图形……
内接
外切,内含……
面积
周长,线段和,线段积,平方和……
平面
立体(球,正方体,长方体,圆柱……)
思维拓展
例2、某农场有一块农田,如图所示,它的边界由圆O的一段圆弧 (M 为此圆弧的中点)和线段EF构成.已知圆O的半径为40米(圆心O在弓形EMF内),现规划在此农田上修建形状为矩形ABCD的温室大棚,其中 AD∥EF,且点A、D 在半圆O上,问如何修建使得矩形ABCD的面积最大?
拓展应用
解:设,(1)当时,点B、C在EF上,此时,
所以
拓展应用
(2)当时,点B、C在圆弧上,此时,,所以
综上,
令的
记区间内余弦值等于的角为(唯一存在),列表得:
拓展应用
+ 0 -
单调递增 极大值 单调递减
又当时,在上的单调减函数,
所以当即时矩形的面积最大.
思维拓展
例3、(2020苏州高三期末18题)为响应“生产发展、生活富裕、乡风文明、村容整洁、管理民主”的社会主义新农村建设,某自然村将村边一块废弃的扇形荒地(如图)租给蜂农养蜂、产蜜与售蜜.已知扇形AOB中,AOB = ,OB= (百米)荒地内规划修建两条直路AB,OC,其中点C在上,(C与A,B不重合),在小路AB与OC的交点D处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区。设,蜂巢区的面积为S(平方百米).
(1)求S关于的函数关系式;
(2)为何值时,蜂巢区的面积S最小,并求此时S的最小值.
思维拓展
思维拓展
思维拓展
例4、(2019年南通二模)如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的半径都是2km,点P在圆Q上,现要在公园内建一块顶点都在圆P上的多边形活动场地.
(1)如图甲,要建的活动场地为△RST,求场地的最大面积;
【解】(1)如右图,过S作SH⊥RT于H,S△RST=
由题意,△RST 在月牙形公园里,RT与圆Q只能相切或相离;
RT左边的部分是一个大小不超过半圆的弓形,则有RT≤4,SH≤2,当且仅当RT切圆Q于P时(如左图),上面两个不等式中等号同时成立.
如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的半径都是2km,点P在圆Q上,现要在公园内建一块顶点都在圆P上的多边形活动场地.(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
思维拓展
解:同(1)的分析,要使得场地面积最大,AD左边的部分是一个大小不超过半圆的弓形,AD必须切圆Q于P,再设.
思维拓展
链接高考
(2018江苏高考)某农场有一块农田,如图所示,它的边界由圆O的一段圆弧 MPN(P为此圆弧的中点)和线段 MN 构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为CPD ,要求A,B 均在线段MN 上,C,D 均在圆弧上.设OC与MN所成的角为.若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3,求当为何值时,能使甲、乙两种蔬菜的年总产值最大.
课堂小结
思考:数学建模的一般过程是什么?
应用题建模四个步骤:“探明关键要素、选择合适参数、探求数学关系、关注变量范围”.
题在书外,根在课本.
课后练习
1、 (2018江苏高考)某农场有一块农田,如图所示,它的边界由圆O的一段圆弧 MPN(P为此圆弧的中点)和线段 MN 构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为CPD ,要求A,B 均在线段MN 上,C,D 均在圆弧上.设OC与MN所成的角为.若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3,求当为何值时,能使甲、乙两种蔬菜的年总产值最大.
课后练习
2、(2019泰州一模)如图,三个小区分别位于扇形OAB的三个顶点上,Q是弧AB的中点,现欲在线段OQ上找一处开挖工作坑P(不与点O,Q重合),为小区铺设三条地下电缆管线PO,PA,PB,已知OA=2千米, ,记∠APQ= θ rad,地下电缆管线的总长度为y千米.
(1) 将y表示成θ的函数,并写出θ的范围;
(2) 请确定工作坑P的位置,使地下电缆管线的总长度最小.
同课章节目录
