8.4.2空间点、直线、平面之间的位置关系 课件(共32张ppt)2023-2024学年高中数学人教A版(2019)必修第二册
文档属性
| 名称 | 8.4.2空间点、直线、平面之间的位置关系 课件(共32张ppt)2023-2024学年高中数学人教A版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
空间点、直线、平面之间的位置关系
教学目标
1.了解空间中两直线间的位置关系.
2.理解空间中直线与平面的位置关系.(重点)
3.掌握空间中平面与平面的位置关系.(难点)
前面我们认识了空间中点、直线、平面之间的一些位置关系,如点在平面内,直线在平面内,两个平面相交,等等.空间中点、直线、平面之间还有其他位置关系吗?
长方体是我们熟悉的空间几何图形,而且长方体中的顶点、棱、表面的关系可以给我们研究空间点、直线、平面的位置关系提供非常有力的直观支持.下面借助长方体进一步研究空间中点、直线、平面之间的位置关系.
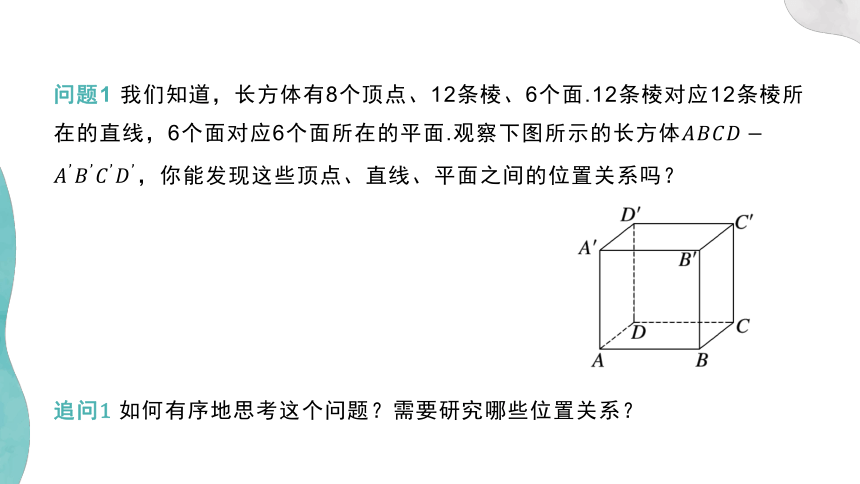
问题1 我们知道,长方体有8个顶点、12条棱、6个面.12条棱对应12条棱所在的直线,6个面对应6个面所在的平面.观察下图所示的长方体,你能发现这些顶点、直线、平面之间的位置关系吗?
追问1 如何有序地思考这个问题?需要研究哪些位置关系?
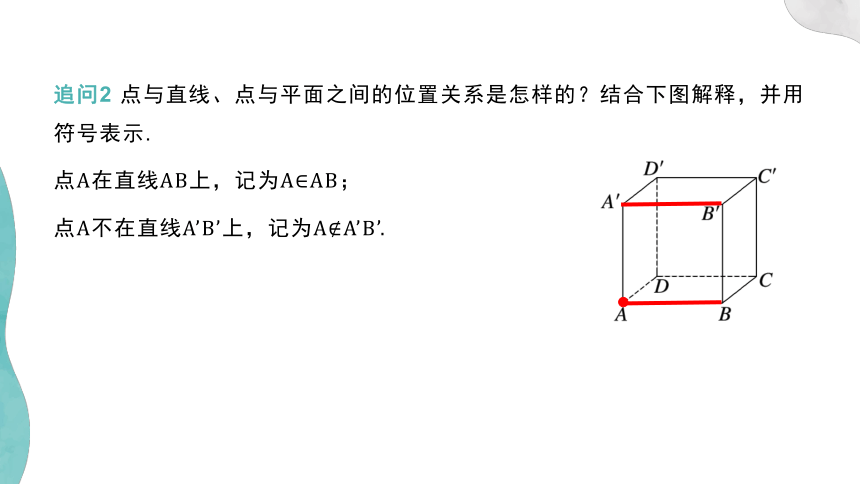
追问2 点与直线、点与平面之间的位置关系是怎样的?结合下图解释,并用符号表示.
点A在直线AB上,记为A∈AB;
点A不在直线A’B’上,记为A A’B’.
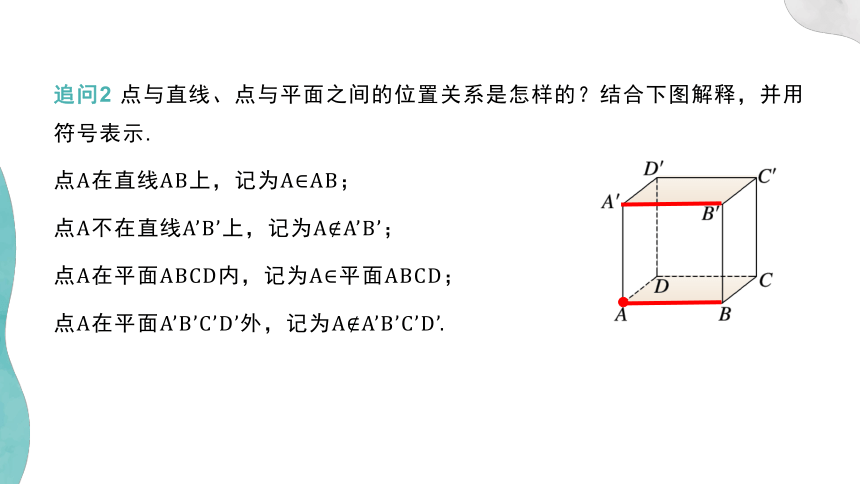
追问2 点与直线、点与平面之间的位置关系是怎样的?结合下图解释,并用符号表示.
点A在直线AB上,记为A∈AB;
点A不在直线A’B’上,记为A A’B’;
点A在平面ABCD内,记为A∈平面ABCD;
点A在平面A’B’C’D’外,记为A A’B’C’D’.
空间中点与直线的位置关系:
点在直线上和点在直线外
空间中点与平面的位置关系:
点在平面内和点在平面外
问题2 观察下图中的长方体,举例说明:空间中直线与直线的位置关系有几种?分别是什么?
平行直线:直线AB与DC在同一个平面内,且没有公共点
相交直线:直线AB与BC在同一个平面内,且有一个公共点
不同在任何一个平面内的直线:直线AB与CC’
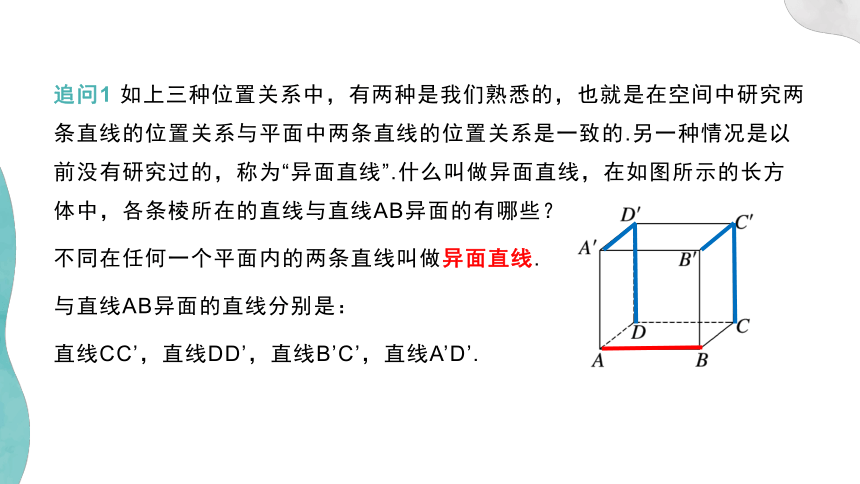
追问1 如上三种位置关系中,有两种是我们熟悉的,也就是在空间中研究两条直线的位置关系与平面中两条直线的位置关系是一致的.另一种情况是以前没有研究过的,称为“异面直线”.什么叫做异面直线,在如图所示的长方体中,各条棱所在的直线与直线AB异面的有哪些?
不同在任何一个平面内的两条直线叫做异面直线.
与直线AB异面的直线分别是:
直线CC’,直线DD’,直线B’C’,直线A’D’.
追问2 你能利用直尺、笔等尝试摆出一些异面直线的位置,并说明这样的两条直线确实是“不同在任何一个平面内”的吗?
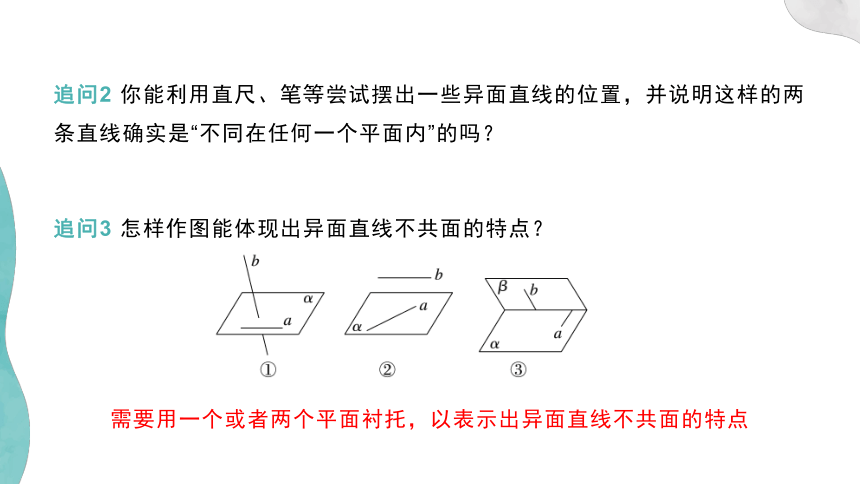
追问3 怎样作图能体现出异面直线不共面的特点?
需要用一个或者两个平面衬托,以表示出异面直线不共面的特点
追问4 你能对空间直线的这三种位置关系进行分类吗?分类标准是什么?分类的结果是什么?
分类标准:两条直线是否共面
分类结果:
追问4 你能对空间直线的这三种位置关系进行分类吗?分类标准是什么?分类的结果是什么?
分类标准:两条直线的公共点个数
分类结果:
例1 如图,在长方体ABCD-A1B1C1D1中,
(1)直线A1B与直线D1C的位置关系是 ;
在长方体ABCD-A1B1C1D1中,A1D1∥BC,A1D1=BC,
∴四边形A1BCD1为平行四边形,
∴A1B∥D1C.
平行
(2)直线A1B与直线B1C的位置关系是 ;
直线A1B与直线B1C不同在任何一个平面内.
异面
(3)直线D1D与直线D1C的位置关系是 ;
直线D1D与直线D1C相交于点D1.
相交
(4)直线AB与直线B1C的位置关系是 .
直线AB与直线B1C不同在任何一个平面内.
异面
跟踪训练1 若a和b是异面直线,b和c是异面直线,则a和c的位置关系是
A.平行 B.异面
C.相交 D.平行、相交或异面
√
可借助长方体来判断.
如图,在长方体ABCD-A′B′C′D′中,A′D′所在直线为a,AB所在直线为b,已知a和b是异面直线,b和c是异面直线,则c可以是长方体ABCD-A′B′C′D′中的B′C′,CC′,DD′.故a和c可以平行、相交或异面.
例2 如图,AB∩,A ,,B .直线AB与具有怎样的位置关系?为什么?
判断异面直线的方法:过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线.
判断异面直线的方法:
1.定义法:不同在任何一个平面内的两条直线叫做异面直线
2.图象法:过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线
3.反证法:判定两条直线既不平行也不相交,那么这两条直线就是异面直线
问题3 观察下图中的长方体ABCD-A’B’C’D’,类比问题2,你能给出研究空间直线与平面位置关系的路径吗?按照确定的研究路径,完成对空间中直线与平面位置关系的研究.
直线AB与平面ABCD有无数个公共点;
直线AB与平面A’B’C’D’没有公共点;
直线AB与平面BB’C’C有且只有一个公共点.
追问 阅读教科书第129页旁白,直线与平面位置关系用图形表示时要注意什么?
一般地,直线在平面内,应把直线画在表示平面的平行四边形内;
直线在平面外,应该把直线或者它的一部分画在表示平面的平行四边形外.
直线与平面的位置关系:
1.直线在平面内——有无数个公共点;
符号表示:
2.直线与平面相交——有且只有一个公共点;
符号表示:
3.直线与平面平行——没有公共点.
符号表示:∥
直线与平面的位置关系:
分类标准:直线是否在平面内
分类结果:
直线与平面的位置关系:
分类标准:直线与平面公共点的个数
分类结果:
例2 (1)若直线上有一点在平面外,则下列结论正确的是
A.直线上所有的点都在平面外
B.直线上有无数多个点都在平面外
C.直线上有无数多个点都在平面内
D.直线上至少有一个点在平面内
√
直线上有一点在平面外,则直线不在平面内,故直线上有无数多个点在平面外.
(2)(多选)若a,b表示直线,α表示平面,则以下命题中是假命题的是
A.若a∥b,b α,则a∥α
B.若a∥α,b∥α,则a∥b
C.若a∥b,b∥α,则a∥α
D.若a∥α,b α,则a∥b或a与b异面
√
√
√
跟踪训练2 下列命题中正确的个数是
①如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面;
②如果直线a和平面α满足a∥α,那么a与平面α内的任何一条直线平行;
③如果直线a,b和平面α满足a∥b,a∥α,b α,那么b∥α.
A.0 B.1
C.2 D.3
√
问题4 类比前面的研究方法,观察下图中的长方体ABCD-A’B’C’D’,你能自主完成对空间中平面与平面的位置关系的研究吗?请你试一试.
两个平面平行 两个平面相交
文字语言
图形语言
符号语言
有一条公共直线
没有公共点
例3 如果在两个平面内分别有一条直线,这两条直线互相平行,那么这两个平面的位置关系一定是
A.平行 B.相交
C.平行或相交 D.无法确定
√
根据题意作图,把自然语言转化为图形语言,即可得出两平面的位置关系,如图所示.
例3 如果在两个平面内分别有一条直线,这两条直线是异面直线,那么这两个平面的位置关系是______________.
如图,a α,b β,a,b异面.
由图知这两个平面可能平行,也可能相交.
跟踪训练3 (多选)以下四个命题中,正确的有
A.在平面α内有两条直线和平面β平行,那么这两个平面平行
B.在平面α内有无数条直线与平面β平行,那么这两个平面平行
C.平面α内△ABC的三个顶点在平面β的同一侧且到平面β的距离相等且不
为0,那么这两个平面平行
D.平面α内有无数个点到平面β的距离相等且不为0,那么这两个平面平行
或相交
√
√
问题5 如图,在长方体ABCD-A’B’C’D’,连接A’B,D’C,你能举出一些图中表示空间直线、平面之间位置关系的例子吗?请你用符号表示这些位置关系.
空间点、直线、平面之间的位置关系
教学目标
1.了解空间中两直线间的位置关系.
2.理解空间中直线与平面的位置关系.(重点)
3.掌握空间中平面与平面的位置关系.(难点)
前面我们认识了空间中点、直线、平面之间的一些位置关系,如点在平面内,直线在平面内,两个平面相交,等等.空间中点、直线、平面之间还有其他位置关系吗?
长方体是我们熟悉的空间几何图形,而且长方体中的顶点、棱、表面的关系可以给我们研究空间点、直线、平面的位置关系提供非常有力的直观支持.下面借助长方体进一步研究空间中点、直线、平面之间的位置关系.
问题1 我们知道,长方体有8个顶点、12条棱、6个面.12条棱对应12条棱所在的直线,6个面对应6个面所在的平面.观察下图所示的长方体,你能发现这些顶点、直线、平面之间的位置关系吗?
追问1 如何有序地思考这个问题?需要研究哪些位置关系?
追问2 点与直线、点与平面之间的位置关系是怎样的?结合下图解释,并用符号表示.
点A在直线AB上,记为A∈AB;
点A不在直线A’B’上,记为A A’B’.
追问2 点与直线、点与平面之间的位置关系是怎样的?结合下图解释,并用符号表示.
点A在直线AB上,记为A∈AB;
点A不在直线A’B’上,记为A A’B’;
点A在平面ABCD内,记为A∈平面ABCD;
点A在平面A’B’C’D’外,记为A A’B’C’D’.
空间中点与直线的位置关系:
点在直线上和点在直线外
空间中点与平面的位置关系:
点在平面内和点在平面外
问题2 观察下图中的长方体,举例说明:空间中直线与直线的位置关系有几种?分别是什么?
平行直线:直线AB与DC在同一个平面内,且没有公共点
相交直线:直线AB与BC在同一个平面内,且有一个公共点
不同在任何一个平面内的直线:直线AB与CC’
追问1 如上三种位置关系中,有两种是我们熟悉的,也就是在空间中研究两条直线的位置关系与平面中两条直线的位置关系是一致的.另一种情况是以前没有研究过的,称为“异面直线”.什么叫做异面直线,在如图所示的长方体中,各条棱所在的直线与直线AB异面的有哪些?
不同在任何一个平面内的两条直线叫做异面直线.
与直线AB异面的直线分别是:
直线CC’,直线DD’,直线B’C’,直线A’D’.
追问2 你能利用直尺、笔等尝试摆出一些异面直线的位置,并说明这样的两条直线确实是“不同在任何一个平面内”的吗?
追问3 怎样作图能体现出异面直线不共面的特点?
需要用一个或者两个平面衬托,以表示出异面直线不共面的特点
追问4 你能对空间直线的这三种位置关系进行分类吗?分类标准是什么?分类的结果是什么?
分类标准:两条直线是否共面
分类结果:
追问4 你能对空间直线的这三种位置关系进行分类吗?分类标准是什么?分类的结果是什么?
分类标准:两条直线的公共点个数
分类结果:
例1 如图,在长方体ABCD-A1B1C1D1中,
(1)直线A1B与直线D1C的位置关系是 ;
在长方体ABCD-A1B1C1D1中,A1D1∥BC,A1D1=BC,
∴四边形A1BCD1为平行四边形,
∴A1B∥D1C.
平行
(2)直线A1B与直线B1C的位置关系是 ;
直线A1B与直线B1C不同在任何一个平面内.
异面
(3)直线D1D与直线D1C的位置关系是 ;
直线D1D与直线D1C相交于点D1.
相交
(4)直线AB与直线B1C的位置关系是 .
直线AB与直线B1C不同在任何一个平面内.
异面
跟踪训练1 若a和b是异面直线,b和c是异面直线,则a和c的位置关系是
A.平行 B.异面
C.相交 D.平行、相交或异面
√
可借助长方体来判断.
如图,在长方体ABCD-A′B′C′D′中,A′D′所在直线为a,AB所在直线为b,已知a和b是异面直线,b和c是异面直线,则c可以是长方体ABCD-A′B′C′D′中的B′C′,CC′,DD′.故a和c可以平行、相交或异面.
例2 如图,AB∩,A ,,B .直线AB与具有怎样的位置关系?为什么?
判断异面直线的方法:过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线.
判断异面直线的方法:
1.定义法:不同在任何一个平面内的两条直线叫做异面直线
2.图象法:过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线
3.反证法:判定两条直线既不平行也不相交,那么这两条直线就是异面直线
问题3 观察下图中的长方体ABCD-A’B’C’D’,类比问题2,你能给出研究空间直线与平面位置关系的路径吗?按照确定的研究路径,完成对空间中直线与平面位置关系的研究.
直线AB与平面ABCD有无数个公共点;
直线AB与平面A’B’C’D’没有公共点;
直线AB与平面BB’C’C有且只有一个公共点.
追问 阅读教科书第129页旁白,直线与平面位置关系用图形表示时要注意什么?
一般地,直线在平面内,应把直线画在表示平面的平行四边形内;
直线在平面外,应该把直线或者它的一部分画在表示平面的平行四边形外.
直线与平面的位置关系:
1.直线在平面内——有无数个公共点;
符号表示:
2.直线与平面相交——有且只有一个公共点;
符号表示:
3.直线与平面平行——没有公共点.
符号表示:∥
直线与平面的位置关系:
分类标准:直线是否在平面内
分类结果:
直线与平面的位置关系:
分类标准:直线与平面公共点的个数
分类结果:
例2 (1)若直线上有一点在平面外,则下列结论正确的是
A.直线上所有的点都在平面外
B.直线上有无数多个点都在平面外
C.直线上有无数多个点都在平面内
D.直线上至少有一个点在平面内
√
直线上有一点在平面外,则直线不在平面内,故直线上有无数多个点在平面外.
(2)(多选)若a,b表示直线,α表示平面,则以下命题中是假命题的是
A.若a∥b,b α,则a∥α
B.若a∥α,b∥α,则a∥b
C.若a∥b,b∥α,则a∥α
D.若a∥α,b α,则a∥b或a与b异面
√
√
√
跟踪训练2 下列命题中正确的个数是
①如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面;
②如果直线a和平面α满足a∥α,那么a与平面α内的任何一条直线平行;
③如果直线a,b和平面α满足a∥b,a∥α,b α,那么b∥α.
A.0 B.1
C.2 D.3
√
问题4 类比前面的研究方法,观察下图中的长方体ABCD-A’B’C’D’,你能自主完成对空间中平面与平面的位置关系的研究吗?请你试一试.
两个平面平行 两个平面相交
文字语言
图形语言
符号语言
有一条公共直线
没有公共点
例3 如果在两个平面内分别有一条直线,这两条直线互相平行,那么这两个平面的位置关系一定是
A.平行 B.相交
C.平行或相交 D.无法确定
√
根据题意作图,把自然语言转化为图形语言,即可得出两平面的位置关系,如图所示.
例3 如果在两个平面内分别有一条直线,这两条直线是异面直线,那么这两个平面的位置关系是______________.
如图,a α,b β,a,b异面.
由图知这两个平面可能平行,也可能相交.
跟踪训练3 (多选)以下四个命题中,正确的有
A.在平面α内有两条直线和平面β平行,那么这两个平面平行
B.在平面α内有无数条直线与平面β平行,那么这两个平面平行
C.平面α内△ABC的三个顶点在平面β的同一侧且到平面β的距离相等且不
为0,那么这两个平面平行
D.平面α内有无数个点到平面β的距离相等且不为0,那么这两个平面平行
或相交
√
√
问题5 如图,在长方体ABCD-A’B’C’D’,连接A’B,D’C,你能举出一些图中表示空间直线、平面之间位置关系的例子吗?请你用符号表示这些位置关系.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
