【五环分层导学-课件】3-1 圆-北师大版数学九(下)
文档属性
| 名称 | 【五环分层导学-课件】3-1 圆-北师大版数学九(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
第三章 圆
第1课 圆
北师大版九年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
(1)一些学生正在做投圈游戏,他们呈“一”字排开.这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形?
不公平,应该排成圆形.
(2)车轮为什么做成圆形?而不做成正方形或三角形等?
【探究1】圆的有关定义及相关概念
(1)平面上到定点的距离等于定长的所有点组成的图形叫做圆.其中定点称%////%,定长称为%////%,以点O为圆心的圆记作%////%,读作“圆O”.
(2)连接圆上任意两点的线段叫%////% ,如右图AB.
经过圆心的弦叫做%////% ,如右图CD.
(3)圆上任意两点间的部分叫圆弧.
圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做%////%.
小于半圆的弧叫做%// //%,如右图,劣弧ABD(记作或).
大于半圆的弧叫做%// //%,如右图,优弧ACD(记作).
(4)%// //%的两个圆叫等圆,在同圆或等圆中,%// //%的弧叫等弧.
圆心
半径
⊙O
弦
直径
半圆
劣弧
优弧
能够重合
能够互相重合
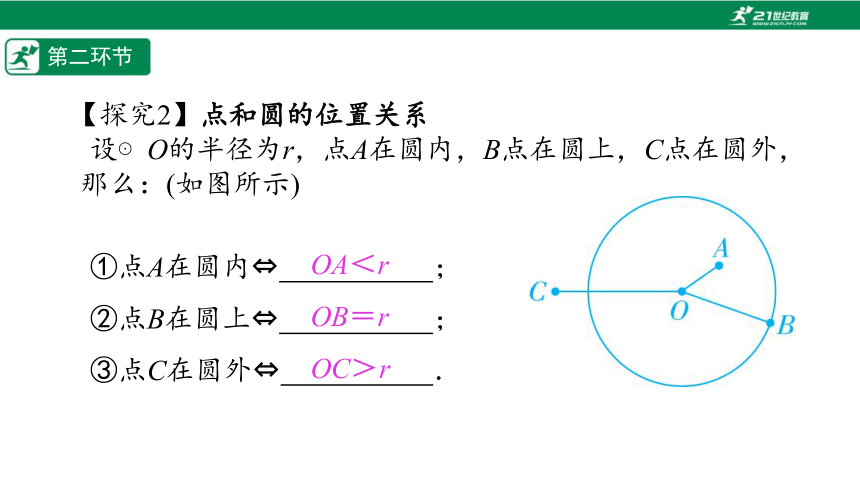
【探究2】点和圆的位置关系
设⊙O的半径为r,点A在圆内,B点在圆上,C点在圆外,那么:(如图所示)
①点A在圆内 %// //%;
②点B在圆上 %// //%;
③点C在圆外 %// //%.
OA<r
OB=r
OC>r
【例题1】如图,已知⊙O的半径r=2 cm,
①当OP=%////% cm时,点P在⊙O上;
②当OA=1 cm时,点A在%// //%;
③当OB=4 cm时,点B在%// //%.
2
⊙O内
⊙O外
【例题2】如图,已知Rt△ABC,Rt△BCD,以BC的中点O为圆心,以BC为直径作⊙O,判断点A和点D与⊙O的位置关系,并说明理由.
解:点A和点D都在⊙O上;理由:连接OA,OD
∵直角三角形斜边的中线等于斜边的一半,
∴OA=OD=OB=OC=BC.//%
∴点A,D到圆心O的距离度等于半径,
∴点A,D都在⊙O上
【例题3】如图,Rt△ABC的两条直角边BC=3,AC=4,CD为斜边AB上的高,若以C为圆心,分别以r=2 cm,r=2.4 cm,r=2.5 cm为半径作⊙C,试判断点D与⊙C的位置关系.
解:在Rt△ABC中,根据勾股定理得AB=5,则CD==2.4;
①当r1=2 cm,2.4>2,点D在圆外;
②当r2=2.4 cm=CD,点D在圆上;
③当r3=2.5 cm时,2.4<2.5,点D在圆内.
1.如图,在△ABC中,∠C=90°,AC=2,BC=4,CM是中线,以C为圆心,为半径作圆,则A、B、M三点在圆外的是 %// ,在圆上的是 %/ ,在圆内的是 %// .
B点
M点
A点
2.点A和⊙O上的最近的点距离为2 cm,和⊙O上的最远的点距离为8 cm,则这圆的半径为////% cm.
3
3.如图,矩形ABCD中,AB=3 cm,AD=4 cm,
(1)以A为圆心,4 cm为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
(2)以A为圆心作⊙A,使B、C、D三点中至少有一个点在圆内,且至少有一个点在圆外,则⊙A的半径r的取值范围是什么?
解;(1)连接AC,∵AB=3cm,AD=4cm,∴AC=5cm,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外;
(2)∵以点A为圆心作⊙A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,
∴⊙A的半径r的取值范围是:3cm<r<5cm.
4.(★)如图,在平面直角坐标系中,有一矩形COAB,其中三个顶点的坐标分别为C(0,3)、O(0,0)、A(4,0),点B在⊙O上.
(1)求点B的坐标;
(2)求⊙O的面积及周长.
解:(1)∵A(4,0),C(0,3),∴B(4,3);
(2)连接OB.
∵OA=4,AB=3,
∴OB5.
∴⊙O的面积=π OB2=25π,周长为2π OB=10π
第三章 圆
第1课 圆
北师大版九年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
(1)一些学生正在做投圈游戏,他们呈“一”字排开.这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形?
不公平,应该排成圆形.
(2)车轮为什么做成圆形?而不做成正方形或三角形等?
【探究1】圆的有关定义及相关概念
(1)平面上到定点的距离等于定长的所有点组成的图形叫做圆.其中定点称%////%,定长称为%////%,以点O为圆心的圆记作%////%,读作“圆O”.
(2)连接圆上任意两点的线段叫%////% ,如右图AB.
经过圆心的弦叫做%////% ,如右图CD.
(3)圆上任意两点间的部分叫圆弧.
圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做%////%.
小于半圆的弧叫做%// //%,如右图,劣弧ABD(记作或).
大于半圆的弧叫做%// //%,如右图,优弧ACD(记作).
(4)%// //%的两个圆叫等圆,在同圆或等圆中,%// //%的弧叫等弧.
圆心
半径
⊙O
弦
直径
半圆
劣弧
优弧
能够重合
能够互相重合
【探究2】点和圆的位置关系
设⊙O的半径为r,点A在圆内,B点在圆上,C点在圆外,那么:(如图所示)
①点A在圆内 %// //%;
②点B在圆上 %// //%;
③点C在圆外 %// //%.
OA<r
OB=r
OC>r
【例题1】如图,已知⊙O的半径r=2 cm,
①当OP=%////% cm时,点P在⊙O上;
②当OA=1 cm时,点A在%// //%;
③当OB=4 cm时,点B在%// //%.
2
⊙O内
⊙O外
【例题2】如图,已知Rt△ABC,Rt△BCD,以BC的中点O为圆心,以BC为直径作⊙O,判断点A和点D与⊙O的位置关系,并说明理由.
解:点A和点D都在⊙O上;理由:连接OA,OD
∵直角三角形斜边的中线等于斜边的一半,
∴OA=OD=OB=OC=BC.//%
∴点A,D到圆心O的距离度等于半径,
∴点A,D都在⊙O上
【例题3】如图,Rt△ABC的两条直角边BC=3,AC=4,CD为斜边AB上的高,若以C为圆心,分别以r=2 cm,r=2.4 cm,r=2.5 cm为半径作⊙C,试判断点D与⊙C的位置关系.
解:在Rt△ABC中,根据勾股定理得AB=5,则CD==2.4;
①当r1=2 cm,2.4>2,点D在圆外;
②当r2=2.4 cm=CD,点D在圆上;
③当r3=2.5 cm时,2.4<2.5,点D在圆内.
1.如图,在△ABC中,∠C=90°,AC=2,BC=4,CM是中线,以C为圆心,为半径作圆,则A、B、M三点在圆外的是 %// ,在圆上的是 %/ ,在圆内的是 %// .
B点
M点
A点
2.点A和⊙O上的最近的点距离为2 cm,和⊙O上的最远的点距离为8 cm,则这圆的半径为////% cm.
3
3.如图,矩形ABCD中,AB=3 cm,AD=4 cm,
(1)以A为圆心,4 cm为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
(2)以A为圆心作⊙A,使B、C、D三点中至少有一个点在圆内,且至少有一个点在圆外,则⊙A的半径r的取值范围是什么?
解;(1)连接AC,∵AB=3cm,AD=4cm,∴AC=5cm,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外;
(2)∵以点A为圆心作⊙A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,
∴⊙A的半径r的取值范围是:3cm<r<5cm.
4.(★)如图,在平面直角坐标系中,有一矩形COAB,其中三个顶点的坐标分别为C(0,3)、O(0,0)、A(4,0),点B在⊙O上.
(1)求点B的坐标;
(2)求⊙O的面积及周长.
解:(1)∵A(4,0),C(0,3),∴B(4,3);
(2)连接OB.
∵OA=4,AB=3,
∴OB5.
∴⊙O的面积=π OB2=25π,周长为2π OB=10π
