【五环分层导学-课件】3-12 单元复习 圆-北师大版数学九(下)
文档属性
| 名称 | 【五环分层导学-课件】3-12 单元复习 圆-北师大版数学九(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 10:39:13 | ||
图片预览











文档简介
(共32张PPT)
第三章 圆
第12课 单元复习
北师大版九年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】举例说明圆在生活中的应用.
【问题2】在同圆或等圆中,圆心角及其所对的弧、弦之间有什么关系?
【问题3】圆周角定理及其推论包含哪些内容?你会证明它们吗?证明过程应用了哪些数学思想方法?
解:车轮、盆子、桶、钥匙扣、各种盖子、戒指、风扇、杯子、摩天轮、桌子等.
解:同圆或等圆,相同的圆心角所对的弧相等,所对的弦相等.
解:圆周角定理:圆周角的度数等于它所对的弧上的圆心角度数的一半;推论:同弧或等弧所对的圆周角相等;证明略.
【问题4】圆内接四边形的对角有什么关系?你是怎么得到的?
【问题5】点与圆有哪些位置关系?怎样判断?直线与圆呢?
【问题6】你对圆内接正多边形有哪些认识?
【问题7】举例说明如何计算弧长,如何计算扇形的面积?略
解:圆内接四边形的对角互补;证明略.
解:点与圆有三种位置关系:点在圆内、点在圆上、点在圆外;通过点到圆心的距离与半径的关系判断;直线与圆的位置关系通过圆心到直线的距离与半径的关系进行判断.
概念:顶点都在同一个圆上的正多边形叫做圆内接正多边形,这个圆叫做该正多边形的外接圆.
【问题8】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现全章知识结构.
考点1:圆的对称性
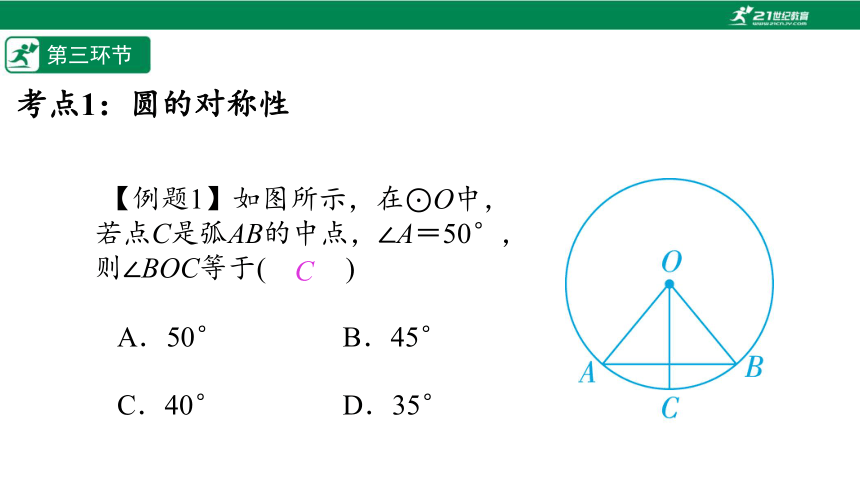
【例题1】如图所示,在⊙O中,若点C是弧AB的中点,∠A=50°,则∠BOC等于(%////%)
A.50° B.45°
C.40° D.35°
C
考点2:圆心角与圆周角
【例题2】如图所示,在⊙O中,=,∠AOB=40°,则∠ADC的度数是(%////%)
A.40° B.30°
C.20° D.15°
C
【例题3】如图所示,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=(%////%)
A.10° B.20° C.30° D.40°
B
考点3:直线与圆的位置关系
【例题4】如图所示,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC .若∠P=40°,则∠ABC的度数为(%////%)
A.20° B.25°
C.40° D.50°
B
【例题5】如图所示,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m=%////%;
(2)当m=2时,d的取值范围是%// //%.
1
1<d<3
【例题6】如图所示,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)求DE的长.
(1)证明:连接OD,
∵AD平分∠BAC,∴∠DAE=∠DAB,
∵OA=OD,∴∠ODA=∠DAO,
∴∠ODA=∠DAE,∴OD∥AE,
∵DE⊥AC,∴OD⊥DE,∴DE是⊙O切线.
(2)解:过点O作OF⊥AC于点F,∴AF=CF=3,
∴OF==4.
∵∠OFE=∠DEF=∠ODE=90°,
∴四边形OFED是矩形,∴DE=OF=4.
考点4:圆内接正多边形
【例题7】如图所示是由两个长方形组成的工件平面图(单位: mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆的最小半径是多少 mm?
解:如图,设圆心为O,连接AO,CO,
∵直线l是它的对称轴,
∴CM=30,AN=40,
∵CM2+OM2=AN2+ON2,
∴302+OM2=402+(70-OM)2,
解得:OM=40,∴OC=50,
∴能完全覆盖这个平面图形的圆面的最小半径是50 mm./
考点5:弧长公式
【例题8】(中考真题)如图所示,在□ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则的长为(%////%)
A. B.
C.π D.2π
C
【例题9】如图所示,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧的长为%//// %.
考点6:扇形面积公式
【例题10】如图所示,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=,以O为圆心,OC为半径作,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.
解:(1)连接OD,∵OA⊥OB,∴∠AOB=90°,
∵CD∥OB,∴∠OCD=90°,在Rt△OCD中,
∵C是AO中点,CD=,∴OD=2CO,
设OC=x,∴x2+()2=(2x)2,
∴x=1,∴OD=2,∴⊙O的半径为2.
(2)∵sin∠CDO==,∴∠CDO=30°,
∵FD∥OB,∴∠DOB=∠ODC=30°,
∴S阴=S△CDO+S扇形OBD-S扇形OCE
=×1×+-=+.
易错点1:概念不清
(1)下列说法正确的个数是(%////%)
①直径是圆中最长的弦;②弧是半圆;③过圆心的直线是直径;④半圆不是弧;⑤长度相等的弧是等弧.
A.1个 B.2个 C.3个 D.4个
(2)在同圆或等圆中,如果弧AB等于弧CD,那么AB与CD的关系是(%////%)
A.AB>CD B.AB=CD C.AB<CD D.AB=2CD
(3)在同圆或等圆中,如果弦AB等于弦CD,那么它们所对应的弧是等弧吗?
A
B
在同圆或等圆中,如果弦AB等于弦CD,那么它们所对应的弧是等弧/
解:当AB、AC在圆心O的同侧时,
如图①所示:过点O作OD⊥AB于D,连接OA,∴AD=AB=,OA=1,
∴cos∠OAB==.∴∠OAB=30°,同理可求:∠OAC=45°,
∴∠BAC=∠OAC-∠OAB=45°-30°=15°;
当AB、AC在圆心O的异侧时,如图②所示:
同理可求:∠OAB=30°,∠OAC=45°.
∴∠BAC=∠OAC+∠OAB=45°+30°=75°.
答:∠BAC的度数为15°或75°.
易错点2:考虑问题不全面
(1)已知△ABC的三个顶点均在⊙O上,且AB=,AC=,⊙O的半径为1,求∠BAC的度数.
(2)知等腰三角形ABC内接于半径为5的⊙O中,如果底边BC的长为8,那么底角的正切值是%// //%.
2或
(3)如图所示,在半径为10 cm的⊙O中,弦AB的长为10 cm,求点O到弦AB的距离及所对劣弧的长度.
解:过点O作OC⊥AB于点C,如图所示:
∵OA=OB=AB=10 cm,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴OC=OA sin60°=10×=5(cm),
的长度==;
即点O到弦AB的距离为5cm,弧AB的长度为cm.
1.分类思想:分类讨论可以使解题过程清晰明了,使解答更为严密完整.在分类时,要注意不重复不遗漏,其关键是确定分类标准.
【例题1】(★)(中考真题)对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图所示,在平面直角坐标系xOy中,直线l:y=x-3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线l运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
解:如图所示,矩形在这两个位置时就是⊙M的“伴侣矩形”,
此时⊙M上的点到矩形各个顶点的距离是1,
根据直线l:y=x-3得:OM=,ON=3,
由勾股定理得:MN==2,
①矩形在x轴下方时,分别过A、D作两轴的垂线AH、DG,
由cos∠ABD=cos∠ONM==,
∴=,AB=,则AD=1,∵DG∥y轴,
∴△MDG∽△MNO,∴=,∴,∴DG=,
∴CG=+=,同理可得:=,∴=,
∴DH=-,∴C(-,-);
②矩形在x轴上方时,同理可得:C(,);
故答案为:(-,-)或(,).
2.转化思想:化未知为已知,化繁为简,化难为易,全面将无求解的问题转化成可以求解的问题,获得解决问题的捷径.本章的转化思想主要体现在:①化“曲面”为“平面”;②将不规则图形面积的求解转化为规则图形面积的求解.
【例题2】(★)(中考真题)如图所示,半圆O的直径AB=2,弦CD∥AB,∠COD=90°,则图中阴影部分的面积为// //%.
3.方程思想:由于圆中涉及的等量关系较多,我们依据已知条件,从“等线“等角”“等积”等方面去建立方程,达到解决问题的目的.
【例题3】(★)(中考真题)如图所示,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接BD,BE.
(1)求证:△ABD∽△AEB;
(2)当=时,求tanE;
(3)在(2)的条件下,作∠BAC
的平分线,与BE交于点F,
若AF=2,求⊙C的半径.
解:(1)∵∠ABC=90°,
∴∠ABD=90°-∠DBC,
由题意知:DE是直径,
∴∠DBE=90°,
∴∠E=90°-∠BDE,
∵BC=CD,
∴∠DBC=∠BDE,∴∠ABD=∠E,
∵∠A=∠A,∴△ABD∽△AEB;
(2)∵AB:BC=4:3,∴设AB=4x,BC=3x,
∴AC==5x,
∵BC=CD=3x,
∴AD=AC-CD=5x-3x=2x,
由(1)可知:△ABD∽△AEB,
∴==,
∴AB2=AD AE,
∴(4x)2=2x·AE,∴AE=8x,
在Rt△DBE中,tanE===;
(3)过点F作FM⊥AE于点M,∵AB:BC=4:3,∴设AB=4x,BC=3x,
∴由(2)可知;AE=8x,AD=2x,∴DE=AE-AD=6x,
∵AF平分∠BAC,∴=,∴==,∵tanE=,
∴cosE=,sinE=,∴=,∴BE=x,
∴EF=BE=x,∴sinE==,∴MF=x,
∵tanE=,∴ME=2MF=x,
∴AM=AE-ME=,
∵AF2=AM2+MF2,
∴4=(x)2+(x)2,∴x=,
∴⊙C的半径为:3x=.
第三章 圆
第12课 单元复习
北师大版九年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】举例说明圆在生活中的应用.
【问题2】在同圆或等圆中,圆心角及其所对的弧、弦之间有什么关系?
【问题3】圆周角定理及其推论包含哪些内容?你会证明它们吗?证明过程应用了哪些数学思想方法?
解:车轮、盆子、桶、钥匙扣、各种盖子、戒指、风扇、杯子、摩天轮、桌子等.
解:同圆或等圆,相同的圆心角所对的弧相等,所对的弦相等.
解:圆周角定理:圆周角的度数等于它所对的弧上的圆心角度数的一半;推论:同弧或等弧所对的圆周角相等;证明略.
【问题4】圆内接四边形的对角有什么关系?你是怎么得到的?
【问题5】点与圆有哪些位置关系?怎样判断?直线与圆呢?
【问题6】你对圆内接正多边形有哪些认识?
【问题7】举例说明如何计算弧长,如何计算扇形的面积?略
解:圆内接四边形的对角互补;证明略.
解:点与圆有三种位置关系:点在圆内、点在圆上、点在圆外;通过点到圆心的距离与半径的关系判断;直线与圆的位置关系通过圆心到直线的距离与半径的关系进行判断.
概念:顶点都在同一个圆上的正多边形叫做圆内接正多边形,这个圆叫做该正多边形的外接圆.
【问题8】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现全章知识结构.
考点1:圆的对称性
【例题1】如图所示,在⊙O中,若点C是弧AB的中点,∠A=50°,则∠BOC等于(%////%)
A.50° B.45°
C.40° D.35°
C
考点2:圆心角与圆周角
【例题2】如图所示,在⊙O中,=,∠AOB=40°,则∠ADC的度数是(%////%)
A.40° B.30°
C.20° D.15°
C
【例题3】如图所示,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=(%////%)
A.10° B.20° C.30° D.40°
B
考点3:直线与圆的位置关系
【例题4】如图所示,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC .若∠P=40°,则∠ABC的度数为(%////%)
A.20° B.25°
C.40° D.50°
B
【例题5】如图所示,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m=%////%;
(2)当m=2时,d的取值范围是%// //%.
1
1<d<3
【例题6】如图所示,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)求DE的长.
(1)证明:连接OD,
∵AD平分∠BAC,∴∠DAE=∠DAB,
∵OA=OD,∴∠ODA=∠DAO,
∴∠ODA=∠DAE,∴OD∥AE,
∵DE⊥AC,∴OD⊥DE,∴DE是⊙O切线.
(2)解:过点O作OF⊥AC于点F,∴AF=CF=3,
∴OF==4.
∵∠OFE=∠DEF=∠ODE=90°,
∴四边形OFED是矩形,∴DE=OF=4.
考点4:圆内接正多边形
【例题7】如图所示是由两个长方形组成的工件平面图(单位: mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆的最小半径是多少 mm?
解:如图,设圆心为O,连接AO,CO,
∵直线l是它的对称轴,
∴CM=30,AN=40,
∵CM2+OM2=AN2+ON2,
∴302+OM2=402+(70-OM)2,
解得:OM=40,∴OC=50,
∴能完全覆盖这个平面图形的圆面的最小半径是50 mm./
考点5:弧长公式
【例题8】(中考真题)如图所示,在□ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则的长为(%////%)
A. B.
C.π D.2π
C
【例题9】如图所示,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧的长为%//// %.
考点6:扇形面积公式
【例题10】如图所示,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=,以O为圆心,OC为半径作,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.
解:(1)连接OD,∵OA⊥OB,∴∠AOB=90°,
∵CD∥OB,∴∠OCD=90°,在Rt△OCD中,
∵C是AO中点,CD=,∴OD=2CO,
设OC=x,∴x2+()2=(2x)2,
∴x=1,∴OD=2,∴⊙O的半径为2.
(2)∵sin∠CDO==,∴∠CDO=30°,
∵FD∥OB,∴∠DOB=∠ODC=30°,
∴S阴=S△CDO+S扇形OBD-S扇形OCE
=×1×+-=+.
易错点1:概念不清
(1)下列说法正确的个数是(%////%)
①直径是圆中最长的弦;②弧是半圆;③过圆心的直线是直径;④半圆不是弧;⑤长度相等的弧是等弧.
A.1个 B.2个 C.3个 D.4个
(2)在同圆或等圆中,如果弧AB等于弧CD,那么AB与CD的关系是(%////%)
A.AB>CD B.AB=CD C.AB<CD D.AB=2CD
(3)在同圆或等圆中,如果弦AB等于弦CD,那么它们所对应的弧是等弧吗?
A
B
在同圆或等圆中,如果弦AB等于弦CD,那么它们所对应的弧是等弧/
解:当AB、AC在圆心O的同侧时,
如图①所示:过点O作OD⊥AB于D,连接OA,∴AD=AB=,OA=1,
∴cos∠OAB==.∴∠OAB=30°,同理可求:∠OAC=45°,
∴∠BAC=∠OAC-∠OAB=45°-30°=15°;
当AB、AC在圆心O的异侧时,如图②所示:
同理可求:∠OAB=30°,∠OAC=45°.
∴∠BAC=∠OAC+∠OAB=45°+30°=75°.
答:∠BAC的度数为15°或75°.
易错点2:考虑问题不全面
(1)已知△ABC的三个顶点均在⊙O上,且AB=,AC=,⊙O的半径为1,求∠BAC的度数.
(2)知等腰三角形ABC内接于半径为5的⊙O中,如果底边BC的长为8,那么底角的正切值是%// //%.
2或
(3)如图所示,在半径为10 cm的⊙O中,弦AB的长为10 cm,求点O到弦AB的距离及所对劣弧的长度.
解:过点O作OC⊥AB于点C,如图所示:
∵OA=OB=AB=10 cm,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴OC=OA sin60°=10×=5(cm),
的长度==;
即点O到弦AB的距离为5cm,弧AB的长度为cm.
1.分类思想:分类讨论可以使解题过程清晰明了,使解答更为严密完整.在分类时,要注意不重复不遗漏,其关键是确定分类标准.
【例题1】(★)(中考真题)对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图所示,在平面直角坐标系xOy中,直线l:y=x-3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线l运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
解:如图所示,矩形在这两个位置时就是⊙M的“伴侣矩形”,
此时⊙M上的点到矩形各个顶点的距离是1,
根据直线l:y=x-3得:OM=,ON=3,
由勾股定理得:MN==2,
①矩形在x轴下方时,分别过A、D作两轴的垂线AH、DG,
由cos∠ABD=cos∠ONM==,
∴=,AB=,则AD=1,∵DG∥y轴,
∴△MDG∽△MNO,∴=,∴,∴DG=,
∴CG=+=,同理可得:=,∴=,
∴DH=-,∴C(-,-);
②矩形在x轴上方时,同理可得:C(,);
故答案为:(-,-)或(,).
2.转化思想:化未知为已知,化繁为简,化难为易,全面将无求解的问题转化成可以求解的问题,获得解决问题的捷径.本章的转化思想主要体现在:①化“曲面”为“平面”;②将不规则图形面积的求解转化为规则图形面积的求解.
【例题2】(★)(中考真题)如图所示,半圆O的直径AB=2,弦CD∥AB,∠COD=90°,则图中阴影部分的面积为// //%.
3.方程思想:由于圆中涉及的等量关系较多,我们依据已知条件,从“等线“等角”“等积”等方面去建立方程,达到解决问题的目的.
【例题3】(★)(中考真题)如图所示,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接BD,BE.
(1)求证:△ABD∽△AEB;
(2)当=时,求tanE;
(3)在(2)的条件下,作∠BAC
的平分线,与BE交于点F,
若AF=2,求⊙C的半径.
解:(1)∵∠ABC=90°,
∴∠ABD=90°-∠DBC,
由题意知:DE是直径,
∴∠DBE=90°,
∴∠E=90°-∠BDE,
∵BC=CD,
∴∠DBC=∠BDE,∴∠ABD=∠E,
∵∠A=∠A,∴△ABD∽△AEB;
(2)∵AB:BC=4:3,∴设AB=4x,BC=3x,
∴AC==5x,
∵BC=CD=3x,
∴AD=AC-CD=5x-3x=2x,
由(1)可知:△ABD∽△AEB,
∴==,
∴AB2=AD AE,
∴(4x)2=2x·AE,∴AE=8x,
在Rt△DBE中,tanE===;
(3)过点F作FM⊥AE于点M,∵AB:BC=4:3,∴设AB=4x,BC=3x,
∴由(2)可知;AE=8x,AD=2x,∴DE=AE-AD=6x,
∵AF平分∠BAC,∴=,∴==,∵tanE=,
∴cosE=,sinE=,∴=,∴BE=x,
∴EF=BE=x,∴sinE==,∴MF=x,
∵tanE=,∴ME=2MF=x,
∴AM=AE-ME=,
∵AF2=AM2+MF2,
∴4=(x)2+(x)2,∴x=,
∴⊙C的半径为:3x=.
