【五环分层导学-课件】1-6 三角函数应用-北师大版数学九(下)
文档属性
| 名称 | 【五环分层导学-课件】1-6 三角函数应用-北师大版数学九(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 10:39:13 | ||
图片预览




文档简介
(共12张PPT)
第一章 直角三角形的边角关系
第6课 三角函数应用
北师大版九年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
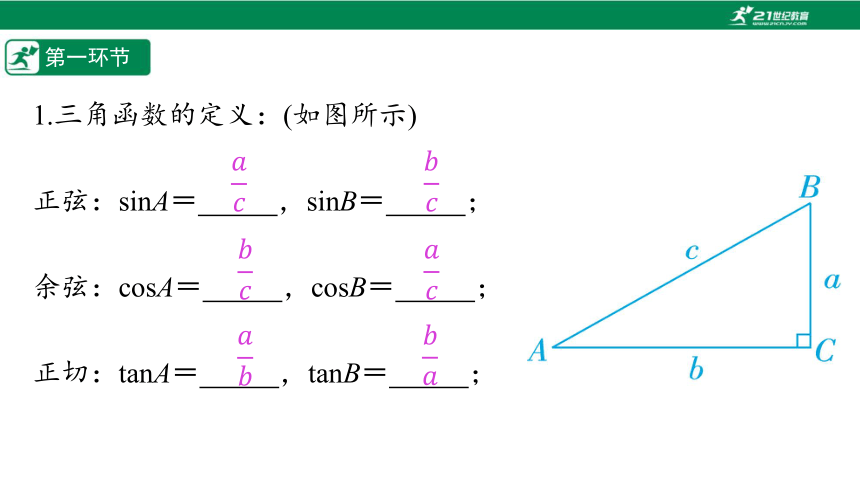
1.三角函数的定义:(如图所示)
正弦:sinA=%////%,sinB=%////%;
余弦:cosA=%////%,cosB=%////%;
正切:tanA=%////%,tanB=%////%;
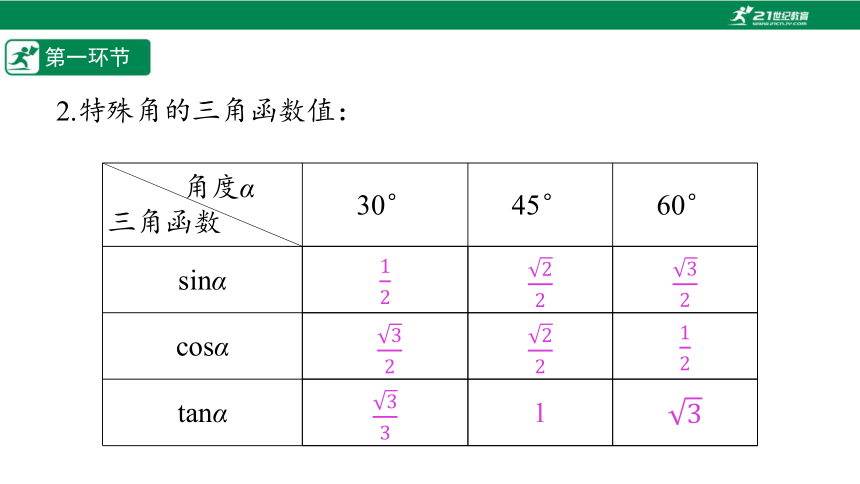
2.特殊角的三角函数值:
角度α 三角函数 30° 45° 60°
sinα
cosα
tanα
%////% %////% %////%
%////% %////% %////%
%////% %//1//% %////%
【探究1】方向角问题
如图,海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后,到达该岛的南偏西25°的C处,之后,货轮继续往东航行,你认为货轮继续向东航行途中会有触礁的危险吗?你是如何想的?与同伴进行交流.
解:作AD⊥BC于点D,设AD=x海里,在Rt△ACD中,
∵∠ADC=90°,∠CAD=25°,∴CD=AD tan25°=tan25° x.
在Rt△ABD中,∵∠ADB=90°,∠BAD=55°,
∴BD=AD tan55°=tan55° x.∵BD-CD=BC,
∴tan55° x-tan25° x=20,∴x=≈20.79>10,
因为A岛到货轮的航线的最短距离大于10海里,
所以货轮继续向东航行没有触礁的危险.
【探究2】测高问题
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m至B处,测得仰角为60°,那么该塔有多高?(小明的身高忽略不计,结果精确到1 m)
解:∵∠DAB=30°,∠DBC=60°,
∴BD=AB=50 m.
∴DC=BD sin60°=50×=25≈43( m ),
答:该塔高为43 m.
变式:深圳某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,如图,已知原楼梯的长度为4 m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01 m)
解:在Rt△ABD中,sin40°==,
∴BC=4sin40°,DC=4cos40°,
在Rt△ACD中,
tan35°=,AC,
调整后的楼梯长度AB=,
∴调整后楼梯加长了:-4≈0.48( m ).
AD=AC-DC≈0.61( m ),
∴楼梯多占0.61 m地面.
【探究3】利用三角函数解决实际问题的一般步骤(或基本思路)?
利用三角函数解决实际问题的一般步骤:
①弄清楚题意,画出示意图;(把实际问题转化为数学问题)
②构造直角三角形;
③利用三角函数解直角三角形.
1.(中考真题)为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时40海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
(1)求∠APB的度数;
(2)已知在灯塔P的周围20海里内有暗礁,问海监船继续向正东方向航行是否安全?
解:过点P作PD⊥AB于点D,
(1)由题意得,∠PAB=30°,∠PBD=60°,
∴∠APB=∠PBD-∠PAB=30°,
(2)由(1)可知∠APB=∠PAB=30°,
∴PB=AB=40(海里),在Rt△PBD中,
PD=BPsin60°=20(海里),20>20,
∴海监船继续向正东方向航行是安全的.
2.(中考模拟)如图,建筑物AB的高为6 m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(tan37°≈0.75,精确到0.01 m)
解:过点A作AE⊥CD于E,则四边形ABDE是矩形,设CE=x m,
在Rt△AEC中,∠AEC=90°,∠CAE=30°,
∴AE==x m,
在Rt△CDM中,CD=CE+DE=CE+AB=(x+6) m,
DM== m,
在Rt△ABM中,BM== m,AE=BD,
∴x=,
解得:x=+3,∴CD=CE+ED=+9≈15.93( m ),
答:通信塔CD的高度约为15.923m.
第一章 直角三角形的边角关系
第6课 三角函数应用
北师大版九年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
1.三角函数的定义:(如图所示)
正弦:sinA=%////%,sinB=%////%;
余弦:cosA=%////%,cosB=%////%;
正切:tanA=%////%,tanB=%////%;
2.特殊角的三角函数值:
角度α 三角函数 30° 45° 60°
sinα
cosα
tanα
%////% %////% %////%
%////% %////% %////%
%////% %//1//% %////%
【探究1】方向角问题
如图,海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后,到达该岛的南偏西25°的C处,之后,货轮继续往东航行,你认为货轮继续向东航行途中会有触礁的危险吗?你是如何想的?与同伴进行交流.
解:作AD⊥BC于点D,设AD=x海里,在Rt△ACD中,
∵∠ADC=90°,∠CAD=25°,∴CD=AD tan25°=tan25° x.
在Rt△ABD中,∵∠ADB=90°,∠BAD=55°,
∴BD=AD tan55°=tan55° x.∵BD-CD=BC,
∴tan55° x-tan25° x=20,∴x=≈20.79>10,
因为A岛到货轮的航线的最短距离大于10海里,
所以货轮继续向东航行没有触礁的危险.
【探究2】测高问题
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m至B处,测得仰角为60°,那么该塔有多高?(小明的身高忽略不计,结果精确到1 m)
解:∵∠DAB=30°,∠DBC=60°,
∴BD=AB=50 m.
∴DC=BD sin60°=50×=25≈43( m ),
答:该塔高为43 m.
变式:深圳某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,如图,已知原楼梯的长度为4 m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01 m)
解:在Rt△ABD中,sin40°==,
∴BC=4sin40°,DC=4cos40°,
在Rt△ACD中,
tan35°=,AC,
调整后的楼梯长度AB=,
∴调整后楼梯加长了:-4≈0.48( m ).
AD=AC-DC≈0.61( m ),
∴楼梯多占0.61 m地面.
【探究3】利用三角函数解决实际问题的一般步骤(或基本思路)?
利用三角函数解决实际问题的一般步骤:
①弄清楚题意,画出示意图;(把实际问题转化为数学问题)
②构造直角三角形;
③利用三角函数解直角三角形.
1.(中考真题)为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时40海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
(1)求∠APB的度数;
(2)已知在灯塔P的周围20海里内有暗礁,问海监船继续向正东方向航行是否安全?
解:过点P作PD⊥AB于点D,
(1)由题意得,∠PAB=30°,∠PBD=60°,
∴∠APB=∠PBD-∠PAB=30°,
(2)由(1)可知∠APB=∠PAB=30°,
∴PB=AB=40(海里),在Rt△PBD中,
PD=BPsin60°=20(海里),20>20,
∴海监船继续向正东方向航行是安全的.
2.(中考模拟)如图,建筑物AB的高为6 m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(tan37°≈0.75,精确到0.01 m)
解:过点A作AE⊥CD于E,则四边形ABDE是矩形,设CE=x m,
在Rt△AEC中,∠AEC=90°,∠CAE=30°,
∴AE==x m,
在Rt△CDM中,CD=CE+DE=CE+AB=(x+6) m,
DM== m,
在Rt△ABM中,BM== m,AE=BD,
∴x=,
解得:x=+3,∴CD=CE+ED=+9≈15.93( m ),
答:通信塔CD的高度约为15.923m.
