【五环分层导学-课件】1-8 单元复习 直角三角形的边角关系-北师大版数学九(下)
文档属性
| 名称 | 【五环分层导学-课件】1-8 单元复习 直角三角形的边角关系-北师大版数学九(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
第一章 直角三角形的边角关系
第8课 单元复习
北师大版九年级下册
第一环节
【问题1】锐角三角函数有哪些?是怎么定义的?
锐角三角函数有正切、正弦、余弦.
①如图,我们把∠A的对边与∠A的邻边的比,
叫做∠A的 ,记作 ,即tanA=.
②如图,在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的 ,
记作 ,即:sinA= .
③如图,在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的 ,
记作 ,即:cosA= .
正切
tanA
正弦
sinA
余弦
cosA
问题导思
第一环节
【问题2】已知锐角,如何用计算器求它的三角函数值?已知三角函数值,如何用计算器求它的对应锐角?
【问题3】如何解直角三角形?
【问题4】如何测量一座楼的高度?你能想出几种方法?
问题导思
第二环节
【问题5】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现全章知识结构.
成果展示
第三环节
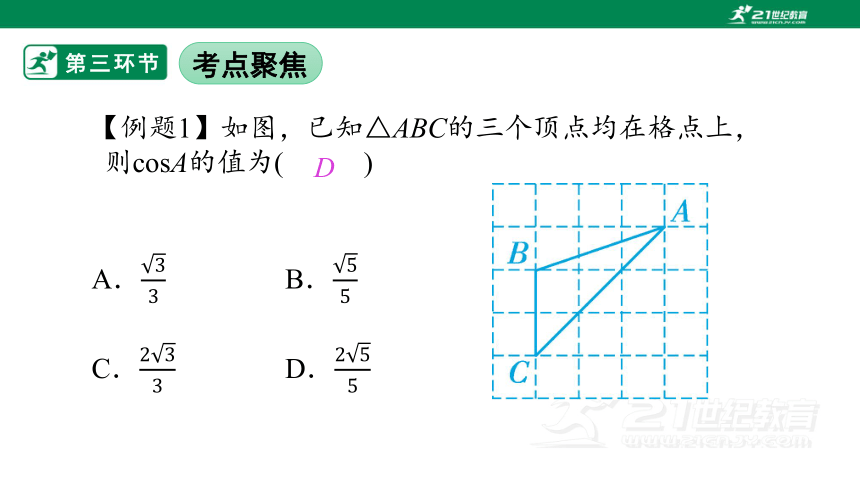
【例题1】如图,已知△ABC的三个顶点均在格点上,则cosA的值为(%////%)
A. B.
C. D.
D
考点聚焦
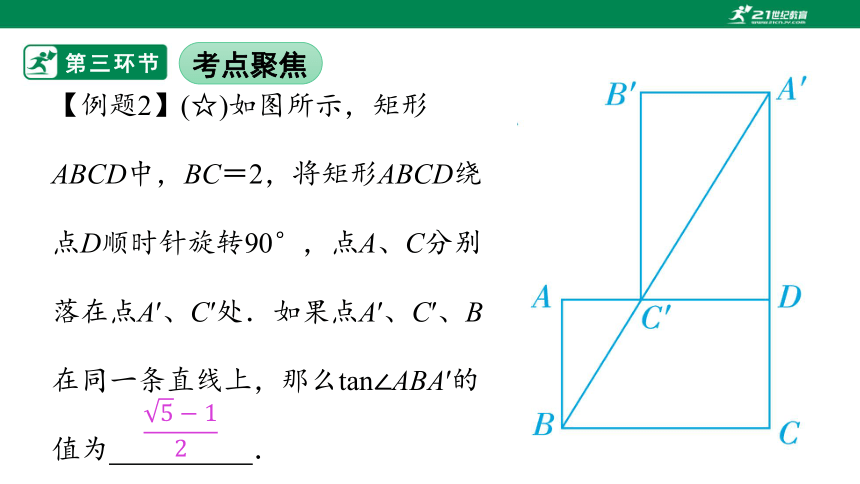
【例题2】(☆)如图所示,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A、C分别落在点A′、C′处.如果点A′、C′、B在同一条直线上,那么tan∠ABA′的值为%// //%.
第三环节
考点聚焦
第三环节
【例题3】(1)计算sin245°+cos30° tan60°,其结果是(%////%)
A.2 B.1 C. D.
(2)计算:tan60°+2sin45°-2cos30°的结果是(%////%)
A.2 B. C. D.1
A
C
考点聚焦
第三环节
【例题4】(中考真题)如图,在△ABC中,∠C=150°,AC=4,tanB=.
(1)求BC的长;
(2)(选做)利用此图形求tan15°的值(精确到0.1,参考数据:=1.4,=1.7,=2.2)
考点聚焦
第三环节
(2)在BC边上取一点M,使得CM=AC,连接AM,如图②所示:
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,
tan15°=tan∠AMD====2-≈0.3.
解:(1)过A作AD⊥BC,交BC的延长线于点D,如图①所示:
在Rt△ADC中,AC=4,∵∠C=150°,∴∠ACD=30°,
∴AD=AC=2,CD=AC cos30°=4×=2,
在Rt△ABD中,tanB===,∴BD=16,
∴BC=BD-CD=16-2;
考点聚焦
第三环节
【例题5】(中考真题)如图,某数学兴趣小组要测量一栋五层居民楼CD的高度.该楼底层为车库,高2.5米;上面五层居住,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米.求居民楼的高度(精确到0.1米,参考数据:≈1.73)
考点聚焦
第三环节
解:设每层楼高为x米,由题意得:
MC′=MC-CC′=2.5-1.5=1米,
∴DC′=5x+1,EC′=4x+1,
在Rt△DC′A′中,∠DA′C′=60°,∴C′A′==(5x+1),
在Rt△EC′B′中,∠EB′C′=30°,∴C′B′==(4x+1),
∵A′B′=C′B′-C′A′=AB,∴(4x+1)-(5x+1)=14,
解得:x≈3.17,∴5×3.17+2.5≈18.4,
则居民楼高约为18.4米.
考点聚焦
第三环节
【例题6】(★)如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45 km/h和36 km/h,经过0.1 h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
第三环节
解:设B处距离码头Ox km,
在Rt△CAO中,∠CAO=45°,∵tan∠CAO=,
∴CO=AO tan∠CAO=(45×0.1+x) tan45°=4.5+x,
在Rt△DBO中,∠DBO=58°,
∵tan∠DBO=,
∴DO=BO tan∠DBO=x tan58°,
∵DC=DO-CO,
∴36×0.1=x tan58°-(4.5+x),
∴x=≈=13.5.
因此,B处距离码头O大约13.5 km.
第四环节
易错点1:考虑问题不全
(1)(★)在Rt△ABC中,两边的长分别为3和4,求此三角形中
最小角的正弦值为%// //%.
(2)(★)在Rt△ABC中,tanB=,求sin=%// //%.
(3)(★)在△ABC中,AB=4,AC=,∠B=60°,求BC的长是%// //%.
或
或
1或者3
易错突破
第四环节
易错点2:正确理解方位角
(1)(★)(中考真题)如图,某校的教室A位于工地O的正西方向,且OA=200 m,一台拖拉机从O点出发,以每秒5 m的速度沿北偏西53°的方向行驶,设拖拉机的噪声污染半径为130 m,则教室A是否在拖拉机的噪声污染范围内?
若不在,请说明理由;若在,
求出教室A受噪声污染的时间有
几秒.(参考数据:sin53°≈0.80,
sin37°≈0.60,tan37°≈0.75)
易错突破
第四环节
解:如图,过点A作AB⊥OM于点B,∵∠MON=53°,
∴∠AOM=90°-53°=37°.
在Rt△ABO中,∠ABO=90°,∵sin∠AOB=,
∴AB=AO sin∠AOB=200×sin37°≈120( m ).∵120 m<130 m.
∴教室A在拖拉机的噪声污染范围内.
根据题意,在OM上取C,D两点,
连接AC,AD,使AC=AD=130 m,
∵AB⊥OM,
∴B为CD的中点,即BC=DB,
∴BC=50( m ),
∴CD=2BC=100( m ).
即影响的时间为=20( s ).
易错突破
第五环节
1.分类讨论思想:在解直角三角形时,我们总是先画出图形,再结合图形分析已知元素和未知元素之间的关系,但当按照所给条件画图情况不唯一时,就要分不同的情况来讨论.
【例题1】(★)(中考真题)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为%// //%.
2或2或2
思想方法
第五环节
2.数形结合思想:从概念的引出、公式的推导、计算化简到解决实际问题,都是通过画图构造直角三角形,找出已知元素和未知元素,从而使问题得以解决.
【例题2】(★)(中考真题)如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,电线杆的高度为%// //%(结果保留根号)
(2+4)米
思想方法
第五环节
3.转化思想:转化思想贯穿于数学学习的始终,例如,利用三角函数定义可以实现边与角的转化,通过添加辅助线可以将非直角三角形转化为直角三角形来解决.此外,在实际应用时,首先将实际问题转化为数学模型,再借助于解直角三角形的知识求解.
【例题3】(★)(中考真题)小明上学途中要经过A,B两地,由于A,B两地之间有一片草坪,所以需要走路线AC,CB,如图,在△ABC中,AB=63 m,∠A=45°,∠B=37°,求AC,CB的长.(结果保留小数点后一位)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,取1.414.)
思想方法
第五环节
解:过点C作CD⊥AB垂足为D,在Rt△ACD中,
tanA=tan45°==1,CD=AD,
sinA=sin45°==,AC=CD .
在Rt△BCD中,
tanB=tan37°=≈0.75,BD=;
sinB=sin37°=≈0.60,CB=.
∵AD+BD=AB=63,∴CD+=63,
解得CD≈27,AC=CD≈1.414×27=38.178≈38.2,
CB=≈=45.0,
答:AC的长约为38.2 m,CB的长约等于45.0 m.
思想方法
第五环节
4.方程思想:方程思想是代数教学的核心内容之一.解直角三角形时,若直角三角形可解,则利用边角关系直接求解;若直角三角形不可解,一般要依据三角函数构建相应的方程,解决问题.
【例题4】(★)(中考真题)如图,垂直于地面的灯柱AB被一钢缆CD固定,CD与地面成45°夹角(∠CDB=45°);为了使灯柱更牢固,在C点上方2米处再新加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),求线段ED的长.(结果精确到0.1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
思想方法
第五环节
解:设BD=x米,则BC=x米,BE=(x+2)米,
在Rt△BDE中,tan∠EDB==,即≈1.33,
解得,x≈6.06,
∵sin∠EDB=,即0.8=,解得:ED≈10.1,
即钢线ED的长度约为10.1米.
思想方法
第一章 直角三角形的边角关系
第8课 单元复习
北师大版九年级下册
第一环节
【问题1】锐角三角函数有哪些?是怎么定义的?
锐角三角函数有正切、正弦、余弦.
①如图,我们把∠A的对边与∠A的邻边的比,
叫做∠A的 ,记作 ,即tanA=.
②如图,在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的 ,
记作 ,即:sinA= .
③如图,在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的 ,
记作 ,即:cosA= .
正切
tanA
正弦
sinA
余弦
cosA
问题导思
第一环节
【问题2】已知锐角,如何用计算器求它的三角函数值?已知三角函数值,如何用计算器求它的对应锐角?
【问题3】如何解直角三角形?
【问题4】如何测量一座楼的高度?你能想出几种方法?
问题导思
第二环节
【问题5】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现全章知识结构.
成果展示
第三环节
【例题1】如图,已知△ABC的三个顶点均在格点上,则cosA的值为(%////%)
A. B.
C. D.
D
考点聚焦
【例题2】(☆)如图所示,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A、C分别落在点A′、C′处.如果点A′、C′、B在同一条直线上,那么tan∠ABA′的值为%// //%.
第三环节
考点聚焦
第三环节
【例题3】(1)计算sin245°+cos30° tan60°,其结果是(%////%)
A.2 B.1 C. D.
(2)计算:tan60°+2sin45°-2cos30°的结果是(%////%)
A.2 B. C. D.1
A
C
考点聚焦
第三环节
【例题4】(中考真题)如图,在△ABC中,∠C=150°,AC=4,tanB=.
(1)求BC的长;
(2)(选做)利用此图形求tan15°的值(精确到0.1,参考数据:=1.4,=1.7,=2.2)
考点聚焦
第三环节
(2)在BC边上取一点M,使得CM=AC,连接AM,如图②所示:
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,
tan15°=tan∠AMD====2-≈0.3.
解:(1)过A作AD⊥BC,交BC的延长线于点D,如图①所示:
在Rt△ADC中,AC=4,∵∠C=150°,∴∠ACD=30°,
∴AD=AC=2,CD=AC cos30°=4×=2,
在Rt△ABD中,tanB===,∴BD=16,
∴BC=BD-CD=16-2;
考点聚焦
第三环节
【例题5】(中考真题)如图,某数学兴趣小组要测量一栋五层居民楼CD的高度.该楼底层为车库,高2.5米;上面五层居住,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米.求居民楼的高度(精确到0.1米,参考数据:≈1.73)
考点聚焦
第三环节
解:设每层楼高为x米,由题意得:
MC′=MC-CC′=2.5-1.5=1米,
∴DC′=5x+1,EC′=4x+1,
在Rt△DC′A′中,∠DA′C′=60°,∴C′A′==(5x+1),
在Rt△EC′B′中,∠EB′C′=30°,∴C′B′==(4x+1),
∵A′B′=C′B′-C′A′=AB,∴(4x+1)-(5x+1)=14,
解得:x≈3.17,∴5×3.17+2.5≈18.4,
则居民楼高约为18.4米.
考点聚焦
第三环节
【例题6】(★)如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45 km/h和36 km/h,经过0.1 h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
第三环节
解:设B处距离码头Ox km,
在Rt△CAO中,∠CAO=45°,∵tan∠CAO=,
∴CO=AO tan∠CAO=(45×0.1+x) tan45°=4.5+x,
在Rt△DBO中,∠DBO=58°,
∵tan∠DBO=,
∴DO=BO tan∠DBO=x tan58°,
∵DC=DO-CO,
∴36×0.1=x tan58°-(4.5+x),
∴x=≈=13.5.
因此,B处距离码头O大约13.5 km.
第四环节
易错点1:考虑问题不全
(1)(★)在Rt△ABC中,两边的长分别为3和4,求此三角形中
最小角的正弦值为%// //%.
(2)(★)在Rt△ABC中,tanB=,求sin=%// //%.
(3)(★)在△ABC中,AB=4,AC=,∠B=60°,求BC的长是%// //%.
或
或
1或者3
易错突破
第四环节
易错点2:正确理解方位角
(1)(★)(中考真题)如图,某校的教室A位于工地O的正西方向,且OA=200 m,一台拖拉机从O点出发,以每秒5 m的速度沿北偏西53°的方向行驶,设拖拉机的噪声污染半径为130 m,则教室A是否在拖拉机的噪声污染范围内?
若不在,请说明理由;若在,
求出教室A受噪声污染的时间有
几秒.(参考数据:sin53°≈0.80,
sin37°≈0.60,tan37°≈0.75)
易错突破
第四环节
解:如图,过点A作AB⊥OM于点B,∵∠MON=53°,
∴∠AOM=90°-53°=37°.
在Rt△ABO中,∠ABO=90°,∵sin∠AOB=,
∴AB=AO sin∠AOB=200×sin37°≈120( m ).∵120 m<130 m.
∴教室A在拖拉机的噪声污染范围内.
根据题意,在OM上取C,D两点,
连接AC,AD,使AC=AD=130 m,
∵AB⊥OM,
∴B为CD的中点,即BC=DB,
∴BC=50( m ),
∴CD=2BC=100( m ).
即影响的时间为=20( s ).
易错突破
第五环节
1.分类讨论思想:在解直角三角形时,我们总是先画出图形,再结合图形分析已知元素和未知元素之间的关系,但当按照所给条件画图情况不唯一时,就要分不同的情况来讨论.
【例题1】(★)(中考真题)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为%// //%.
2或2或2
思想方法
第五环节
2.数形结合思想:从概念的引出、公式的推导、计算化简到解决实际问题,都是通过画图构造直角三角形,找出已知元素和未知元素,从而使问题得以解决.
【例题2】(★)(中考真题)如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,电线杆的高度为%// //%(结果保留根号)
(2+4)米
思想方法
第五环节
3.转化思想:转化思想贯穿于数学学习的始终,例如,利用三角函数定义可以实现边与角的转化,通过添加辅助线可以将非直角三角形转化为直角三角形来解决.此外,在实际应用时,首先将实际问题转化为数学模型,再借助于解直角三角形的知识求解.
【例题3】(★)(中考真题)小明上学途中要经过A,B两地,由于A,B两地之间有一片草坪,所以需要走路线AC,CB,如图,在△ABC中,AB=63 m,∠A=45°,∠B=37°,求AC,CB的长.(结果保留小数点后一位)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,取1.414.)
思想方法
第五环节
解:过点C作CD⊥AB垂足为D,在Rt△ACD中,
tanA=tan45°==1,CD=AD,
sinA=sin45°==,AC=CD .
在Rt△BCD中,
tanB=tan37°=≈0.75,BD=;
sinB=sin37°=≈0.60,CB=.
∵AD+BD=AB=63,∴CD+=63,
解得CD≈27,AC=CD≈1.414×27=38.178≈38.2,
CB=≈=45.0,
答:AC的长约为38.2 m,CB的长约等于45.0 m.
思想方法
第五环节
4.方程思想:方程思想是代数教学的核心内容之一.解直角三角形时,若直角三角形可解,则利用边角关系直接求解;若直角三角形不可解,一般要依据三角函数构建相应的方程,解决问题.
【例题4】(★)(中考真题)如图,垂直于地面的灯柱AB被一钢缆CD固定,CD与地面成45°夹角(∠CDB=45°);为了使灯柱更牢固,在C点上方2米处再新加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),求线段ED的长.(结果精确到0.1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
思想方法
第五环节
解:设BD=x米,则BC=x米,BE=(x+2)米,
在Rt△BDE中,tan∠EDB==,即≈1.33,
解得,x≈6.06,
∵sin∠EDB=,即0.8=,解得:ED≈10.1,
即钢线ED的长度约为10.1米.
思想方法
