圆的切线的识别
图片预览



文档简介
(共12张PPT)
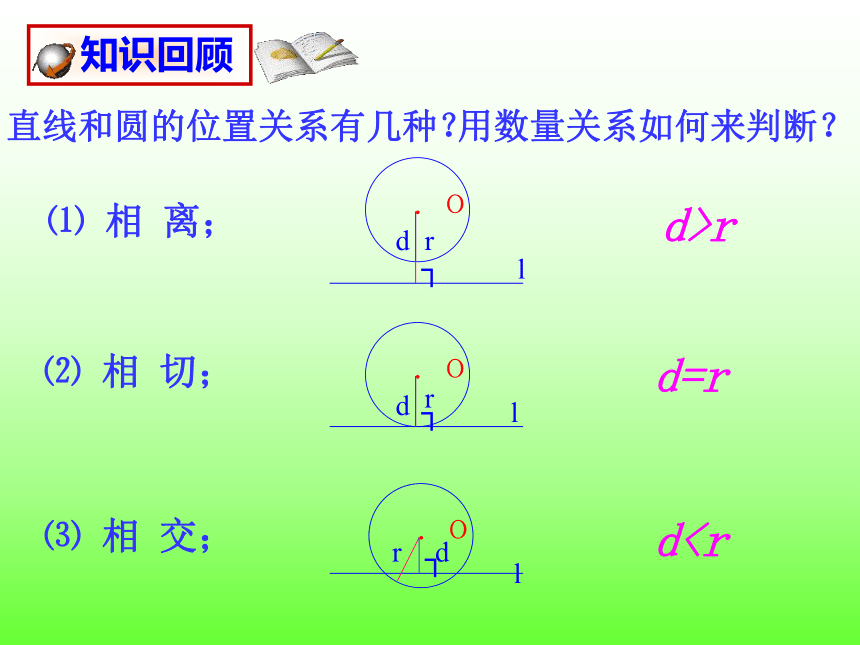
直线和圆的位置关系有几种?
知识回顾
⑴ 相 离;
⑵ 相 切;
⑶ 相 交;
dd=r
d>r
用数量关系如何来判断?
.O
l
┐
d
r
.O
l
┐
d
r
.O
l
┐
d
r
观察与思考
问题1:下雨天,转动的雨伞上的水滴是
顺着伞的什么方向飞出去的
问题2:砂轮转动时,火花是沿着砂轮的
什么方向飞出去的
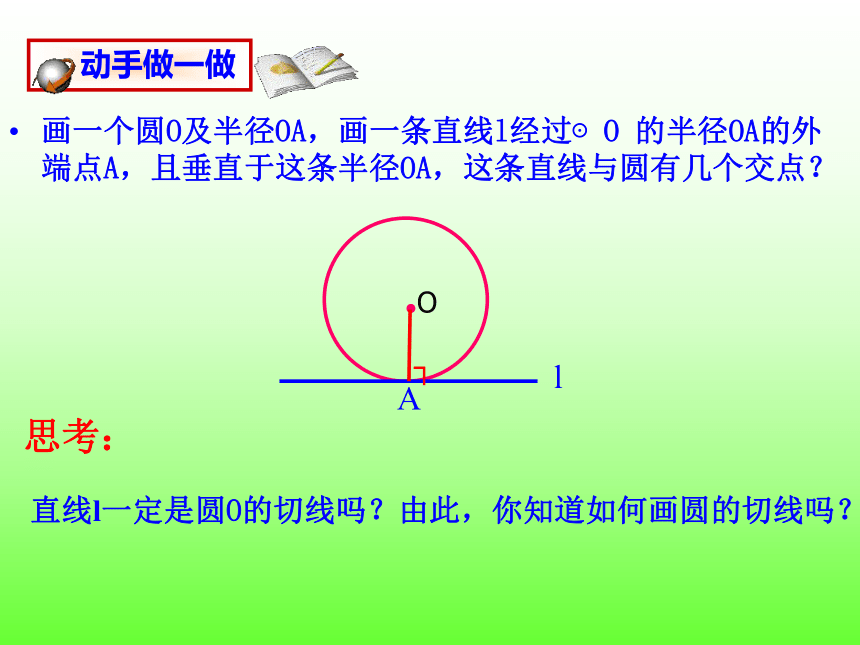
动手做一做
●O
画一个圆O及半径OA,画一条直线l经过⊙O 的半径OA的外端点A,且垂直于这条半径OA,这条直线与圆有几个交点?
┐
A
l
直线l一定是圆O的切线吗?由此,你知道如何画圆的切线吗?
思考:
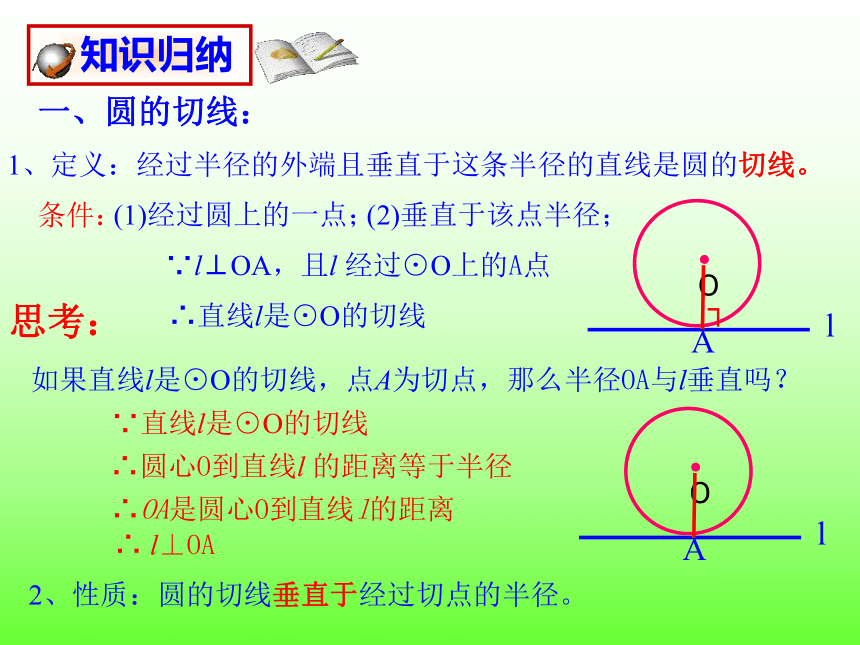
1、定义:经过半径的外端且垂直于这条半径的直线是圆的切线。
条件:
(1)经过圆上的一点;
如果直线l是⊙O的切线,点A为切点,那么半径OA与l垂直吗?
一、圆的切线:
∵直线l是⊙O的切线
知识归纳
(2)垂直于该点半径;
●O
┐
A
l
思考:
●O
A
l
2、性质:圆的切线垂直于经过切点的半径。
∴圆心O到直线l 的距离等于半径
∴OA是圆心O到直线l的距离
∴ l⊥OA
∵l⊥OA,且l 经过⊙O上的A点
∴直线l是⊙O的切线
例1、如右图所示,已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?为什么?
解:直线AB是⊙O的切线 。理由如下:
在圆O 中,
又∵∠OAB+ ∠OBA+ ∠AOB = 180°
例题欣赏
∵因为AB=OA,∠OBA=45°(已知)
∴∠AOB=∠OBA=45°(等边对等角)
∴∠OAB=180°-∠OBA-∠AOB=90°
∴ 直线AB⊥OA
又∵直线AB经过⊙O 上的A点
∴直线AB是⊙O的切线
A
B
O
●
练一练
1、判断题:
2、以三角形的一边为直径的圆恰好与另一边相切,则此三角形是__________三角形
直角
×
(1) 垂直于圆的半径的直线一定是这个圆的切线。 ( )
(2) 过圆的半径的外端的直线一定是这个圆的切线 。( )
×
练一练
3、如图,AB是⊙O的直径,∠B=45°,AC=AB。
AC是⊙O的切线吗?为什么?
解:AC是⊙O的切线 。理由如下:
又∵∠BAC+∠B+∠C = 180°
∵ AC=AB , ∠B=45°(已知)
∴ 直线AC⊥AB
又∵直线AC经过⊙O 上的A点
∴直线AC是⊙O的切线
∴∠C=∠B=45°(等边对等角)
∴∠ BAC = 180°-∠B-∠C=90°
O
●
A
B
C
练一练
4、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D。BD是⊙O的切线吗?为什么?
解:BD是⊙O的切线 。连结OD。
又∵∠B+∠BOD+∠BDO = 180°
∵ OA=OD , ∠BAD=30°(已知)
∴ 直线AC⊥AB
又∵直线BD 经过⊙O上的D点
∴直线BD是⊙O的切线
∴∠ODA=∠A=30°(等边对等角)
∴∠BOD=∠A+∠ODA=60°
O
●
A
B
C
D
∴∠BDO=180°-∠B-∠BOD=90°
例2、如右图所示,已知OC平分∠AOB,D是OC上任意一点,⊙D与OA相切于点E。那么,OB是⊙D的切线吗?请说明理由。
例题欣赏
E
C
D
●
解:OB是⊙D的切线 。理由如下:
又∵ OC平分∠AOB, DF⊥OB
∴ DF = DE
又∵ DF⊥OB,
∴ OB是⊙D的切线 。
∴ OE⊥OA
∵ OA 与⊙D 相切于点E
连结DE,过D点作DF⊥OB,垂足为F。
A
B
O
F
┐
即 d = r
小结:
1、如何判定一条直线是已知圆的切线?
(1)和圆只有一个公共点的直线是圆的切线;
(2)和圆心的距离等于半径的直线是圆的切线;
(3)过半径外端且和半径垂直的直线是圆的切线;
(d=r)
A 、经过圆上的一点;
B、 垂直于半径;
2、圆的切线有什么性质?
圆的切线垂直于经过切点的半径。
知 识 的 升 华
1、课本P63习题23.2 第7题
独立
作业
祝 你 成 功!
2、练习册 P45第8题
结 束 寄 语
不经历风雨,怎能见彩虹!
下 课
直线和圆的位置关系有几种?
知识回顾
⑴ 相 离;
⑵ 相 切;
⑶ 相 交;
d
d>r
用数量关系如何来判断?
.O
l
┐
d
r
.O
l
┐
d
r
.O
l
┐
d
r
观察与思考
问题1:下雨天,转动的雨伞上的水滴是
顺着伞的什么方向飞出去的
问题2:砂轮转动时,火花是沿着砂轮的
什么方向飞出去的
动手做一做
●O
画一个圆O及半径OA,画一条直线l经过⊙O 的半径OA的外端点A,且垂直于这条半径OA,这条直线与圆有几个交点?
┐
A
l
直线l一定是圆O的切线吗?由此,你知道如何画圆的切线吗?
思考:
1、定义:经过半径的外端且垂直于这条半径的直线是圆的切线。
条件:
(1)经过圆上的一点;
如果直线l是⊙O的切线,点A为切点,那么半径OA与l垂直吗?
一、圆的切线:
∵直线l是⊙O的切线
知识归纳
(2)垂直于该点半径;
●O
┐
A
l
思考:
●O
A
l
2、性质:圆的切线垂直于经过切点的半径。
∴圆心O到直线l 的距离等于半径
∴OA是圆心O到直线l的距离
∴ l⊥OA
∵l⊥OA,且l 经过⊙O上的A点
∴直线l是⊙O的切线
例1、如右图所示,已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?为什么?
解:直线AB是⊙O的切线 。理由如下:
在圆O 中,
又∵∠OAB+ ∠OBA+ ∠AOB = 180°
例题欣赏
∵因为AB=OA,∠OBA=45°(已知)
∴∠AOB=∠OBA=45°(等边对等角)
∴∠OAB=180°-∠OBA-∠AOB=90°
∴ 直线AB⊥OA
又∵直线AB经过⊙O 上的A点
∴直线AB是⊙O的切线
A
B
O
●
练一练
1、判断题:
2、以三角形的一边为直径的圆恰好与另一边相切,则此三角形是__________三角形
直角
×
(1) 垂直于圆的半径的直线一定是这个圆的切线。 ( )
(2) 过圆的半径的外端的直线一定是这个圆的切线 。( )
×
练一练
3、如图,AB是⊙O的直径,∠B=45°,AC=AB。
AC是⊙O的切线吗?为什么?
解:AC是⊙O的切线 。理由如下:
又∵∠BAC+∠B+∠C = 180°
∵ AC=AB , ∠B=45°(已知)
∴ 直线AC⊥AB
又∵直线AC经过⊙O 上的A点
∴直线AC是⊙O的切线
∴∠C=∠B=45°(等边对等角)
∴∠ BAC = 180°-∠B-∠C=90°
O
●
A
B
C
练一练
4、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D。BD是⊙O的切线吗?为什么?
解:BD是⊙O的切线 。连结OD。
又∵∠B+∠BOD+∠BDO = 180°
∵ OA=OD , ∠BAD=30°(已知)
∴ 直线AC⊥AB
又∵直线BD 经过⊙O上的D点
∴直线BD是⊙O的切线
∴∠ODA=∠A=30°(等边对等角)
∴∠BOD=∠A+∠ODA=60°
O
●
A
B
C
D
∴∠BDO=180°-∠B-∠BOD=90°
例2、如右图所示,已知OC平分∠AOB,D是OC上任意一点,⊙D与OA相切于点E。那么,OB是⊙D的切线吗?请说明理由。
例题欣赏
E
C
D
●
解:OB是⊙D的切线 。理由如下:
又∵ OC平分∠AOB, DF⊥OB
∴ DF = DE
又∵ DF⊥OB,
∴ OB是⊙D的切线 。
∴ OE⊥OA
∵ OA 与⊙D 相切于点E
连结DE,过D点作DF⊥OB,垂足为F。
A
B
O
F
┐
即 d = r
小结:
1、如何判定一条直线是已知圆的切线?
(1)和圆只有一个公共点的直线是圆的切线;
(2)和圆心的距离等于半径的直线是圆的切线;
(3)过半径外端且和半径垂直的直线是圆的切线;
(d=r)
A 、经过圆上的一点;
B、 垂直于半径;
2、圆的切线有什么性质?
圆的切线垂直于经过切点的半径。
知 识 的 升 华
1、课本P63习题23.2 第7题
独立
作业
祝 你 成 功!
2、练习册 P45第8题
结 束 寄 语
不经历风雨,怎能见彩虹!
下 课
