人教版数学 八年级下册18.2.3 正方形 同步练习(含解析)
文档属性
| 名称 | 人教版数学 八年级下册18.2.3 正方形 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 201.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 13:06:43 | ||
图片预览

文档简介
18.2.3 正方形 同步练习 人教版数学 八年级下册
学校:______姓名:______班级:______考号:______
一、单选题(共10小题)
1.下列说法不正确的是( )
A.对角线互相垂直的矩形一定是正方形
B.对角线相等的菱形一定是正方形
C.对角线互相垂直且相等的平行四边形一定是正方形
D.顺次连接任意对角线相等的四边形的各边中点所得的四边形一定是正方形
2.一个长方形在平面直角坐标系中,三个顶点的坐标分别是(,)、(,)、(,),则第四个顶点的坐标是( )
A.(,) B.(,) C.(,) D.(,)
3.如图,将长为、宽为的矩形纸片分割成个三角形后,拼成面积为的正方形,则不等于( )
A. B. C. D.
4.如图,在菱形中,对角线与相交于点添加以下条件,能判定菱形是正方形的是( )
A. B. C. D.
5.如图,在矩形纸片中,,.现将其沿对折,使得点落在边上的点处,折痕与边交于点,则的长为( )
A. B. C. D.
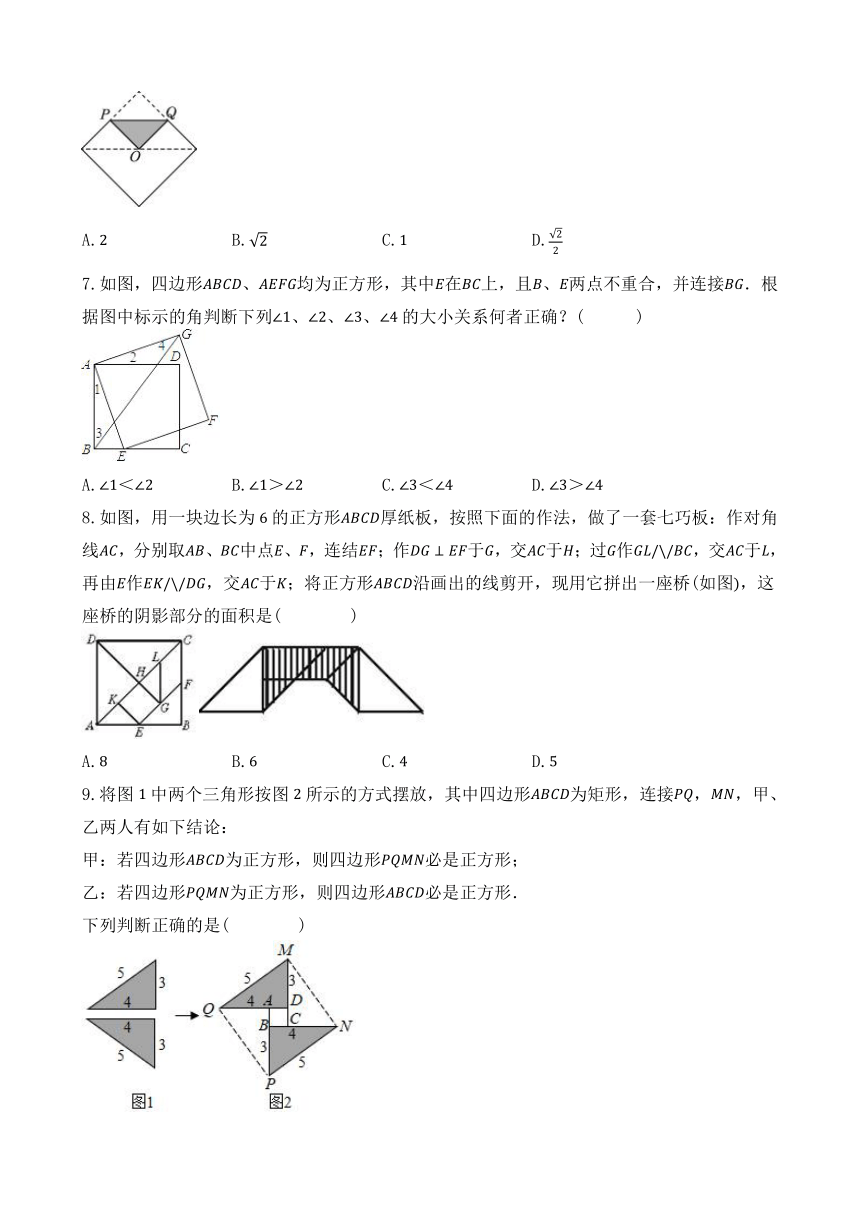
6.如图,现有一块边长为的正方形巾,将其一角折叠至方巾的中心位置,则折痕的长为( )
A. B. C. D.
7.如图,四边形、均为正方形,其中在上,且、两点不重合,并连接.根据图中标示的角判断下列、、、的大小关系何者正确?( )
A.< B.> C.< D.>
8.如图,用一块边长为的正方形厚纸板,按照下面的作法,做了一套七巧板:作对角线,分别取、中点、,连结;作于,交于;过作,交于,再由作,交于;将正方形沿画出的线剪开,现用它拼出一座桥(如图,这座桥的阴影部分的面积是( )
A. B. C. D.
9.将图中两个三角形按图所示的方式摆放,其中四边形为矩形,连接,,甲、乙两人有如下结论:
甲:若四边形为正方形,则四边形必是正方形;
乙:若四边形为正方形,则四边形必是正方形.
下列判断正确的是( )
A.甲正确,乙不正确 B.甲不正确,乙正确
C.甲、乙都不正确 D.甲、乙都正确
10.如图,中,,,,、为线段上两动点(不与端点重合)且连接,,当点运动时,对的描述正确的是( )
A.等于定值 B.有最大值
C.有最小值 D.有最小值
二、填空题(共8小题)
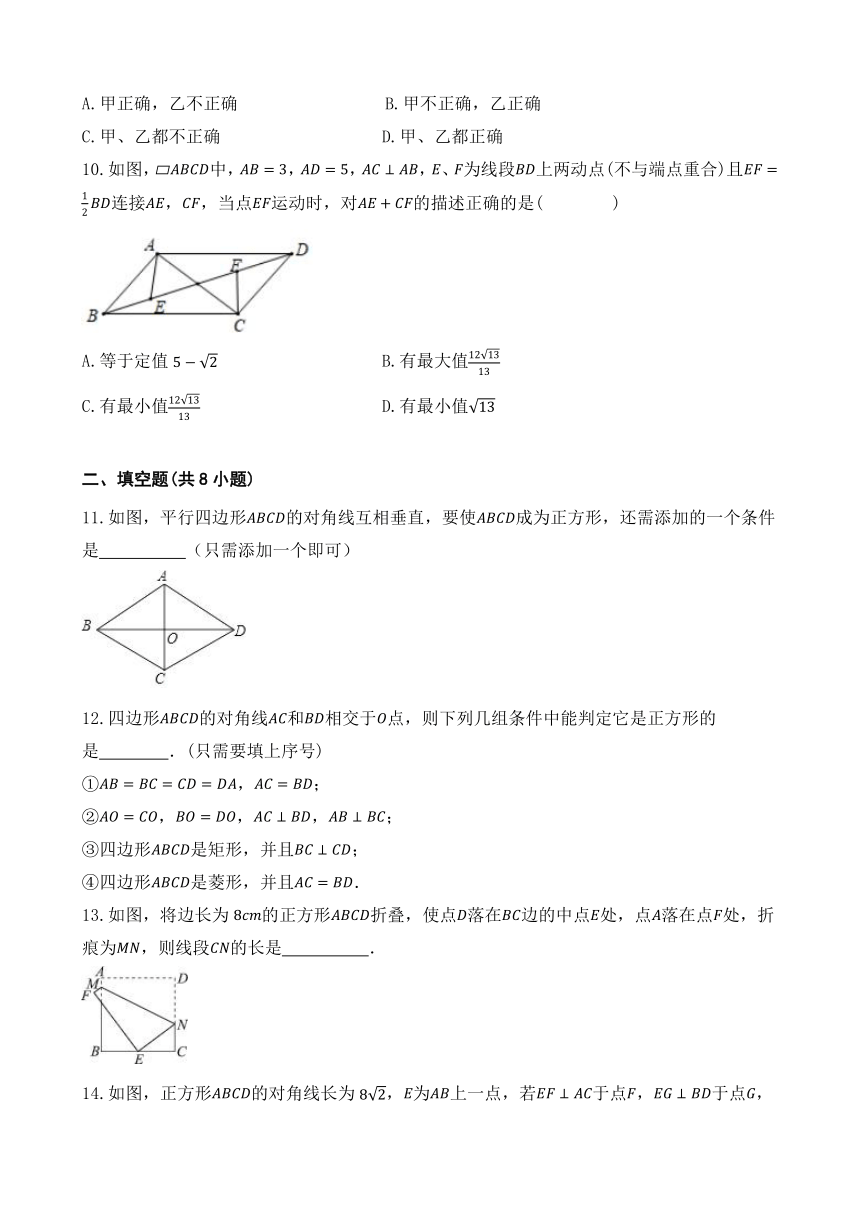
11.如图,平行四边形的对角线互相垂直,要使成为正方形,还需添加的一个条件是 (只需添加一个即可)
12.四边形的对角线和相交于点,则下列几组条件中能判定它是正方形的是 .(只需要填上序号)
①,;
②,,,;
③四边形是矩形,并且;
④四边形是菱形,并且.
13.如图,将边长为的正方形折叠,使点落在边的中点处,点落在点处,折痕为,则线段的长是 .
14.如图,正方形的对角线长为,为上一点,若于点,于点,则 .
15.如图,已知两点在正方形的对角线上移动,,连接,并延长分别交于两点,则 .
16.如图,在平面直角坐标系中,一次函数的图象经过正方形的顶点和,则正方形的面积为
17.将个边长为的正方形按照如图所示方式摆放,,,,,,是正方形对角线的交点,那么阴影部分面积之和等于 .
18.我国数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图,它是用八个全等的直角三角形拼接而成,记图中正方形,正方形,正方形的面积分别为,,,若,则的值是 .
三、解答题(共5小题)
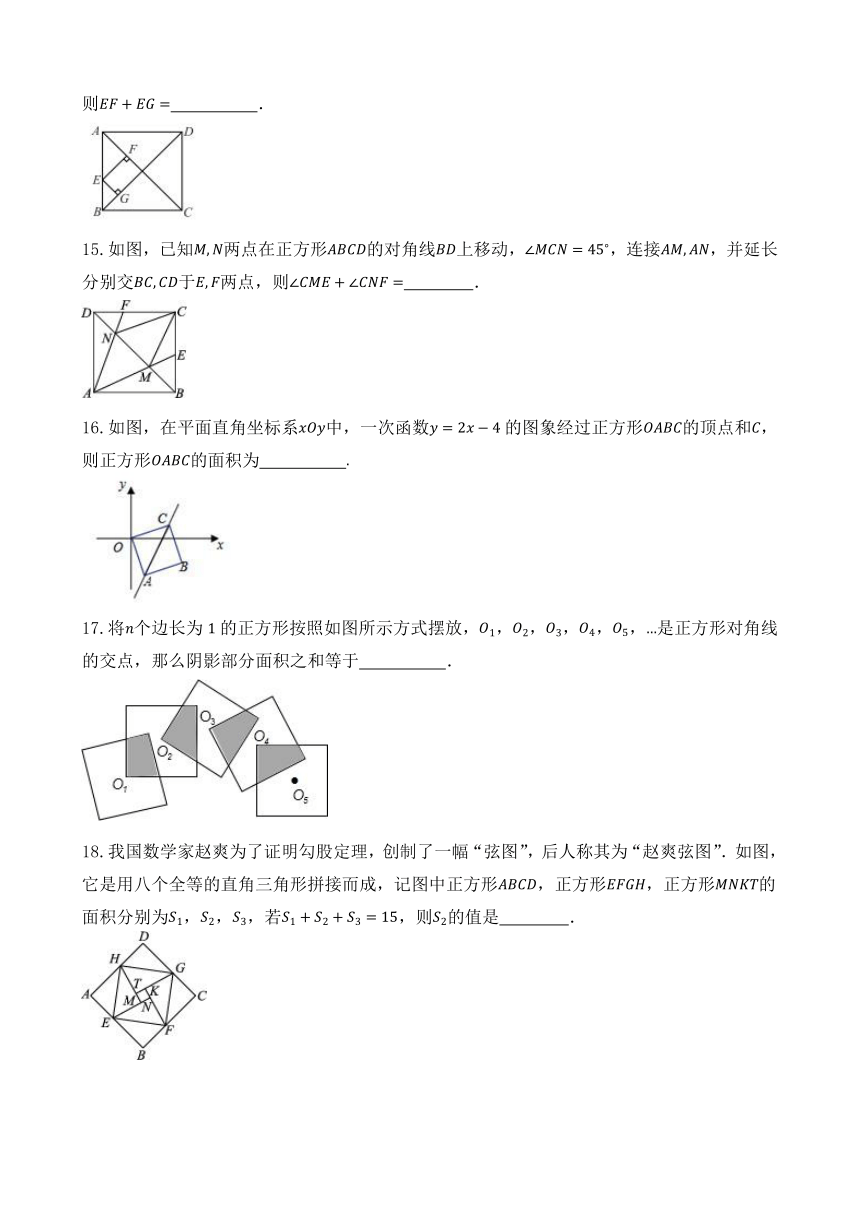
19.如图所示,四边形是正方形,两条对角线相交于点,求、的度数.
20.如图,直线分别与轴、轴交于两点,是坐标平面内的两点,是否存在这样的点使以为顶点的四边形是正方形?若存在,求点的坐标;若不存在,请说明理由.
21.如图所示,长方形被分成六个大小不一的正方形,已知中间一个小正方形面积为,求长方形中最大正方形与最小正方形的面积之差.
22.如图,等边三角形的顶点,在矩形的边,上,且.
求证:矩形是正方形.
23.如图,在菱形中,对角线,相交于点,点,在对角线上,且,.求证:四边形是正方形.
参考答案
1.【答案】D
【解析】、对角线互相垂直的矩形一定是正方形,正确,不合题意;
、对角线相等的菱形一定是正方形,正确,不合题意;
、对角线互相垂直且相等的平行四边形一定是正方形,正确,不合题意;
、顺次连接任意对角线相等的四边形的各边中点所得的四边形一定是菱形,故此选项错误,符合题意.
故选:.
通过灵活运用平行四边形的性质和矩形的性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.
2.【答案】C
【解析】过(,)、(,)两点分别作轴、轴的平行线,交点为(,),即为第四个顶点坐标.
故选:.
3.【答案】A
【解析】如图所示.将长为、宽为的矩形纸片分割成个三角形后,拼成面积为的正方形,则可以为,,,故.故选.
4.【答案】C
【解析】四边形是菱形,
故选项不符合题意;
当时
是等边三角形,
菱形不是正方形,故选项不符合题意;
当时,菱形是正方形,故选项符合题意.
故选.
5.【答案】D
【解析】由折叠可知,,且四边形是正方形,从而,
故,
故选.
6.【答案】B
【解析】如图:
四边形是正方形,
.
由折叠的性质得,
,
.
同理,
四边形是正方形,
,
,,,
,
.
7.【答案】D
【解析】∵四边形、均为正方形,
∴,
∵,
,
∴,
在中,>,
∵四边形是正方形,
∴,
∴>,
∴>.
故选.
8.【答案】A
【解析】本题考查正方形的性质 根据裁剪及拼图的情况可知,阴影部分的面积是原正方形面积的一半,据此计算即可.
解:观察两个图形,分析易得阴影部分的面积即是直角三角形的面积,即正方形的面积的一半;
因为正方形的面积, 阴影部分的面积是.
故选.
9.【答案】B
【解析】若是正方形,可设,
,
,即
取值不同则的长度不同,甲不正确
若四边形为正方形,则
,
且,
在和中,
,
即
矩形是正方形
乙正确
故选.
10.【答案】D
【解析】如图,
四边形是平行四边形,
,,
,
,,,
,,,
,
,
,
当时,,
若此时,则,
而时,
,
与不垂直,
,故,错误;
当为的中点,为的中点时,
,
,
同理:,
,
即的最小值为,故错误,正确;
故选:.
11.【答案】答案不唯一,如
【解析】条件为,
理由是:
∵平行四边形的对角线互相垂直,
∴四边形是菱形,
∵,
∴四边形是正方形,
据此可知答案为:.
12.【答案】①②④
13.【答案】
14.【答案】
【解析】如图,∵四边形是正方形,
∴,
又∵,
∴,
即,
∴.
15.【答案】
【解析】由正方形的对称性可得,,,
,
.
16.【答案】
【解析】本题考查了正方形的性质及面积公式的运用,垂直的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,一次函数图象上点的坐标的特征的运用,解答时证明三角形全等是关键过点作轴于点,过点作轴于点,由正方形的性质就可以得出,就可以得出,,由一次函数的图象经过正方形的顶点和,设点,就可以得代入解析式就可以求出的值,由正方形的面积等于就可以求出结论.
解:如图,过点作轴于点,过点作轴于点,
∴
∵四边形是正方形,
∴,.
∵,
∴,
∴,
∴.
在和中,
,
∴,
∴,
∵一次函数的图象经过正方形的顶点和,设点,
∴,,
∴,,
∴,
∴,
∴.
∴,,
在中,由勾股定理,得.
,
,
故答案为.
17.【答案】()
【解析】【分析】此题考查了正方形的性质,解决本题的关键是得到个这样的正方形重叠部分(阴影部分的面积和的计算方法,难点是求得一个阴影部分的面积.
根据题意可得,阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则个这样的正方形重叠部分即为阴影部分的和,问题得解.
【解答】解:由题意可得阴影部分面积等于正方形面积的,即是.
个这样的正方形重叠部分(阴影部分的面积和为.
故答案为:.
18.【答案】
【解析】由于图中的小三角形都是全等的,可用表示一个三角形的面积,
则,
所以
所以
19.【答案】因为正方形也是菱形,
所以,即.
因为正方形是矩形,
所以,则.
所以为等腰直角三角形.
所以.
【解析】直接根据正方形的性质定理求解.
20.【答案】解:由题意,得.
当是正方形的一边,且在直线下方时,
如图①,则或.
当是正方形的一边,且在直线上方时,
如图②,则或.
当是正方形的对角线时,如图③,则或.
综上,存在点使以为顶点的四边形是正方形,点的坐标为.
21.【答案】由题意,得,,,
∵,
∴.
∴.
∴.
∴两正方形的面积差为
.
【解析】因为小正方形的面积为,所以它的边长为,显然它是最小的正方形.其余正方形的边长是,,,可见边长为的正方形是最大的,因此可求得两正方形面积差.
22.【答案】∵四边形是矩形,
∴.
∵是等边三角形,
∴,,
∵,
∴,
∴,
∴,
∴,
∴矩形是正方形.
23.【答案】证明:四边形是菱形,
,,,
,
,
,四边形是菱形.
,
,即,
四边形是正方形.
学校:______姓名:______班级:______考号:______
一、单选题(共10小题)
1.下列说法不正确的是( )
A.对角线互相垂直的矩形一定是正方形
B.对角线相等的菱形一定是正方形
C.对角线互相垂直且相等的平行四边形一定是正方形
D.顺次连接任意对角线相等的四边形的各边中点所得的四边形一定是正方形
2.一个长方形在平面直角坐标系中,三个顶点的坐标分别是(,)、(,)、(,),则第四个顶点的坐标是( )
A.(,) B.(,) C.(,) D.(,)
3.如图,将长为、宽为的矩形纸片分割成个三角形后,拼成面积为的正方形,则不等于( )
A. B. C. D.
4.如图,在菱形中,对角线与相交于点添加以下条件,能判定菱形是正方形的是( )
A. B. C. D.
5.如图,在矩形纸片中,,.现将其沿对折,使得点落在边上的点处,折痕与边交于点,则的长为( )
A. B. C. D.
6.如图,现有一块边长为的正方形巾,将其一角折叠至方巾的中心位置,则折痕的长为( )
A. B. C. D.
7.如图,四边形、均为正方形,其中在上,且、两点不重合,并连接.根据图中标示的角判断下列、、、的大小关系何者正确?( )
A.< B.> C.< D.>
8.如图,用一块边长为的正方形厚纸板,按照下面的作法,做了一套七巧板:作对角线,分别取、中点、,连结;作于,交于;过作,交于,再由作,交于;将正方形沿画出的线剪开,现用它拼出一座桥(如图,这座桥的阴影部分的面积是( )
A. B. C. D.
9.将图中两个三角形按图所示的方式摆放,其中四边形为矩形,连接,,甲、乙两人有如下结论:
甲:若四边形为正方形,则四边形必是正方形;
乙:若四边形为正方形,则四边形必是正方形.
下列判断正确的是( )
A.甲正确,乙不正确 B.甲不正确,乙正确
C.甲、乙都不正确 D.甲、乙都正确
10.如图,中,,,,、为线段上两动点(不与端点重合)且连接,,当点运动时,对的描述正确的是( )
A.等于定值 B.有最大值
C.有最小值 D.有最小值
二、填空题(共8小题)
11.如图,平行四边形的对角线互相垂直,要使成为正方形,还需添加的一个条件是 (只需添加一个即可)
12.四边形的对角线和相交于点,则下列几组条件中能判定它是正方形的是 .(只需要填上序号)
①,;
②,,,;
③四边形是矩形,并且;
④四边形是菱形,并且.
13.如图,将边长为的正方形折叠,使点落在边的中点处,点落在点处,折痕为,则线段的长是 .
14.如图,正方形的对角线长为,为上一点,若于点,于点,则 .
15.如图,已知两点在正方形的对角线上移动,,连接,并延长分别交于两点,则 .
16.如图,在平面直角坐标系中,一次函数的图象经过正方形的顶点和,则正方形的面积为
17.将个边长为的正方形按照如图所示方式摆放,,,,,,是正方形对角线的交点,那么阴影部分面积之和等于 .
18.我国数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图,它是用八个全等的直角三角形拼接而成,记图中正方形,正方形,正方形的面积分别为,,,若,则的值是 .
三、解答题(共5小题)
19.如图所示,四边形是正方形,两条对角线相交于点,求、的度数.
20.如图,直线分别与轴、轴交于两点,是坐标平面内的两点,是否存在这样的点使以为顶点的四边形是正方形?若存在,求点的坐标;若不存在,请说明理由.
21.如图所示,长方形被分成六个大小不一的正方形,已知中间一个小正方形面积为,求长方形中最大正方形与最小正方形的面积之差.
22.如图,等边三角形的顶点,在矩形的边,上,且.
求证:矩形是正方形.
23.如图,在菱形中,对角线,相交于点,点,在对角线上,且,.求证:四边形是正方形.
参考答案
1.【答案】D
【解析】、对角线互相垂直的矩形一定是正方形,正确,不合题意;
、对角线相等的菱形一定是正方形,正确,不合题意;
、对角线互相垂直且相等的平行四边形一定是正方形,正确,不合题意;
、顺次连接任意对角线相等的四边形的各边中点所得的四边形一定是菱形,故此选项错误,符合题意.
故选:.
通过灵活运用平行四边形的性质和矩形的性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.
2.【答案】C
【解析】过(,)、(,)两点分别作轴、轴的平行线,交点为(,),即为第四个顶点坐标.
故选:.
3.【答案】A
【解析】如图所示.将长为、宽为的矩形纸片分割成个三角形后,拼成面积为的正方形,则可以为,,,故.故选.
4.【答案】C
【解析】四边形是菱形,
故选项不符合题意;
当时
是等边三角形,
菱形不是正方形,故选项不符合题意;
当时,菱形是正方形,故选项符合题意.
故选.
5.【答案】D
【解析】由折叠可知,,且四边形是正方形,从而,
故,
故选.
6.【答案】B
【解析】如图:
四边形是正方形,
.
由折叠的性质得,
,
.
同理,
四边形是正方形,
,
,,,
,
.
7.【答案】D
【解析】∵四边形、均为正方形,
∴,
∵,
,
∴,
在中,>,
∵四边形是正方形,
∴,
∴>,
∴>.
故选.
8.【答案】A
【解析】本题考查正方形的性质 根据裁剪及拼图的情况可知,阴影部分的面积是原正方形面积的一半,据此计算即可.
解:观察两个图形,分析易得阴影部分的面积即是直角三角形的面积,即正方形的面积的一半;
因为正方形的面积, 阴影部分的面积是.
故选.
9.【答案】B
【解析】若是正方形,可设,
,
,即
取值不同则的长度不同,甲不正确
若四边形为正方形,则
,
且,
在和中,
,
即
矩形是正方形
乙正确
故选.
10.【答案】D
【解析】如图,
四边形是平行四边形,
,,
,
,,,
,,,
,
,
,
当时,,
若此时,则,
而时,
,
与不垂直,
,故,错误;
当为的中点,为的中点时,
,
,
同理:,
,
即的最小值为,故错误,正确;
故选:.
11.【答案】答案不唯一,如
【解析】条件为,
理由是:
∵平行四边形的对角线互相垂直,
∴四边形是菱形,
∵,
∴四边形是正方形,
据此可知答案为:.
12.【答案】①②④
13.【答案】
14.【答案】
【解析】如图,∵四边形是正方形,
∴,
又∵,
∴,
即,
∴.
15.【答案】
【解析】由正方形的对称性可得,,,
,
.
16.【答案】
【解析】本题考查了正方形的性质及面积公式的运用,垂直的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,一次函数图象上点的坐标的特征的运用,解答时证明三角形全等是关键过点作轴于点,过点作轴于点,由正方形的性质就可以得出,就可以得出,,由一次函数的图象经过正方形的顶点和,设点,就可以得代入解析式就可以求出的值,由正方形的面积等于就可以求出结论.
解:如图,过点作轴于点,过点作轴于点,
∴
∵四边形是正方形,
∴,.
∵,
∴,
∴,
∴.
在和中,
,
∴,
∴,
∵一次函数的图象经过正方形的顶点和,设点,
∴,,
∴,,
∴,
∴,
∴.
∴,,
在中,由勾股定理,得.
,
,
故答案为.
17.【答案】()
【解析】【分析】此题考查了正方形的性质,解决本题的关键是得到个这样的正方形重叠部分(阴影部分的面积和的计算方法,难点是求得一个阴影部分的面积.
根据题意可得,阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则个这样的正方形重叠部分即为阴影部分的和,问题得解.
【解答】解:由题意可得阴影部分面积等于正方形面积的,即是.
个这样的正方形重叠部分(阴影部分的面积和为.
故答案为:.
18.【答案】
【解析】由于图中的小三角形都是全等的,可用表示一个三角形的面积,
则,
所以
所以
19.【答案】因为正方形也是菱形,
所以,即.
因为正方形是矩形,
所以,则.
所以为等腰直角三角形.
所以.
【解析】直接根据正方形的性质定理求解.
20.【答案】解:由题意,得.
当是正方形的一边,且在直线下方时,
如图①,则或.
当是正方形的一边,且在直线上方时,
如图②,则或.
当是正方形的对角线时,如图③,则或.
综上,存在点使以为顶点的四边形是正方形,点的坐标为.
21.【答案】由题意,得,,,
∵,
∴.
∴.
∴.
∴两正方形的面积差为
.
【解析】因为小正方形的面积为,所以它的边长为,显然它是最小的正方形.其余正方形的边长是,,,可见边长为的正方形是最大的,因此可求得两正方形面积差.
22.【答案】∵四边形是矩形,
∴.
∵是等边三角形,
∴,,
∵,
∴,
∴,
∴,
∴,
∴矩形是正方形.
23.【答案】证明:四边形是菱形,
,,,
,
,
,四边形是菱形.
,
,即,
四边形是正方形.
