人教版数学 八年级下册18.1.2 平行四边形的判定同步练习(含解析)
文档属性
| 名称 | 人教版数学 八年级下册18.1.2 平行四边形的判定同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 109.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 00:00:00 | ||
图片预览


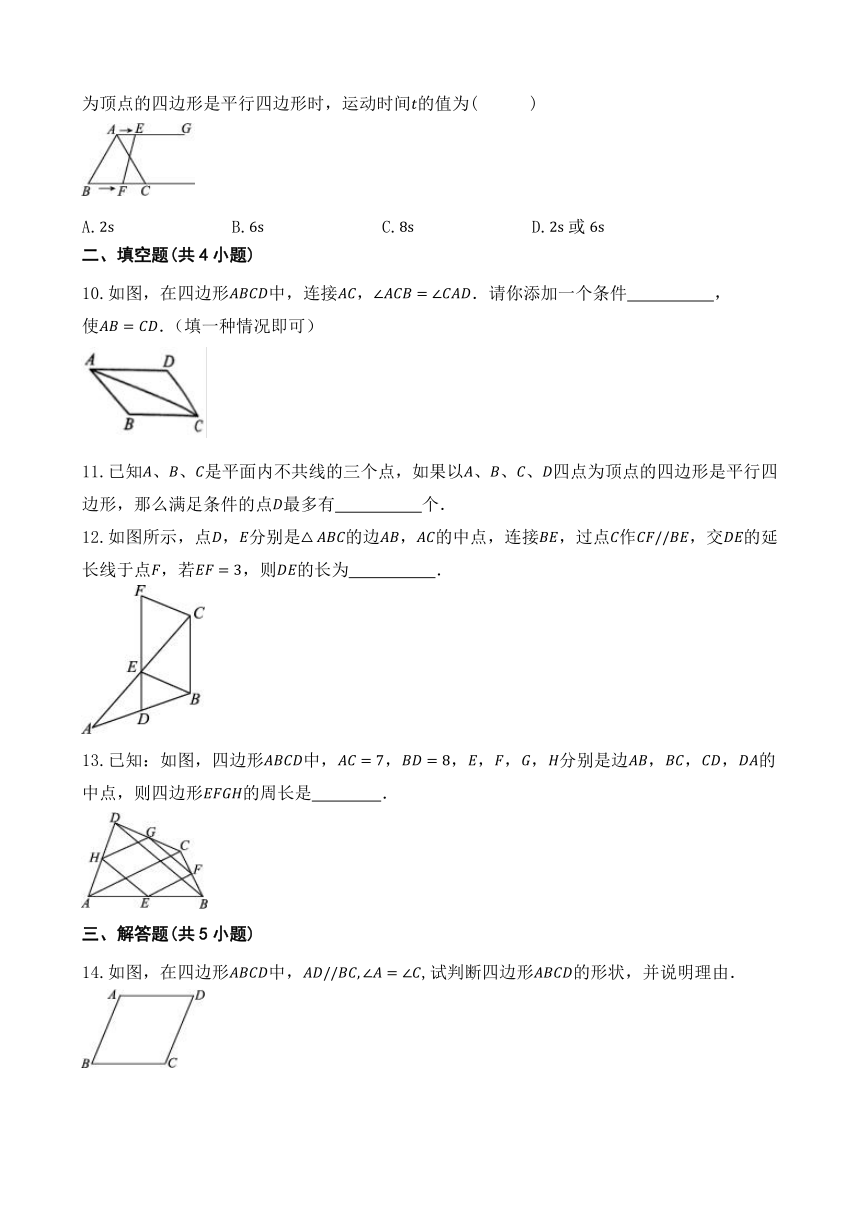

文档简介
18.1.2 平行四边形的判定 同步练习 人教版数学 八年级下册
学校:______姓名:______班级:______考号:______
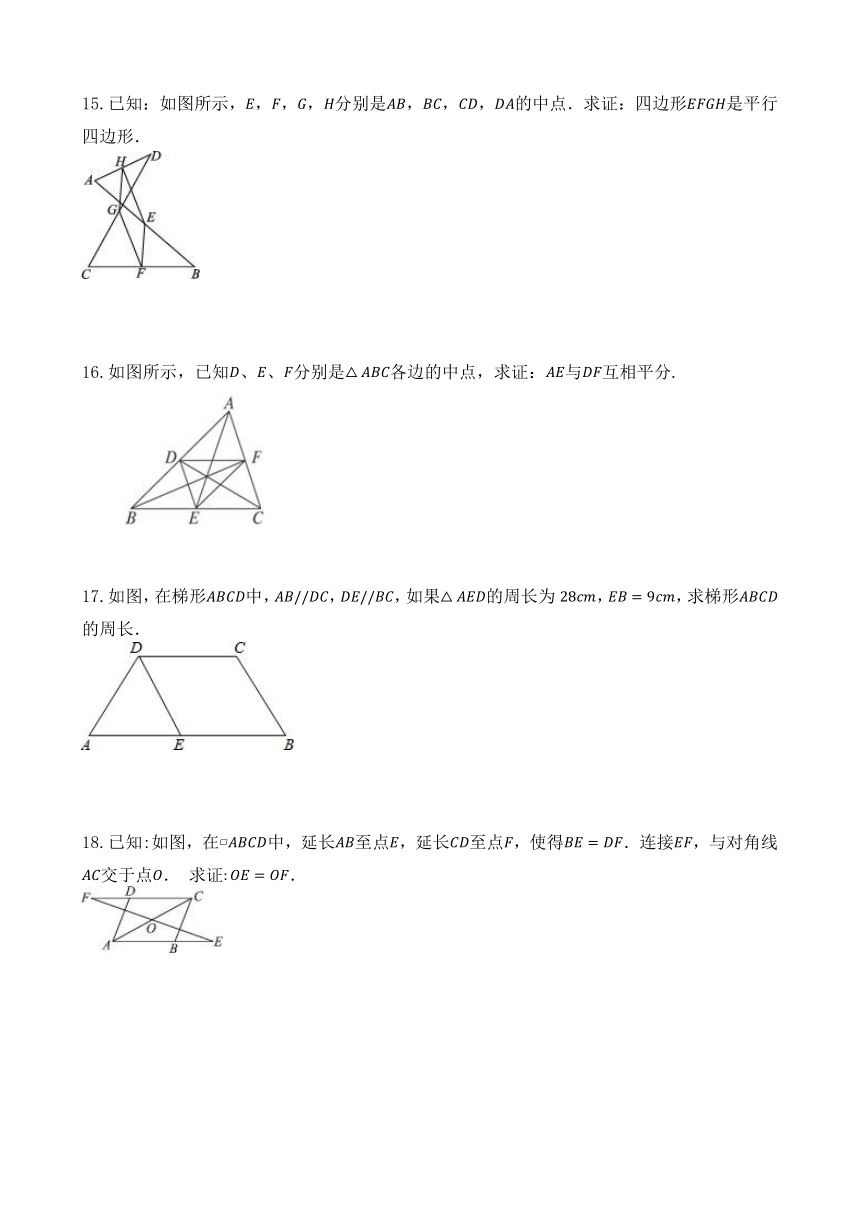
一、单选题(共9小题)
1.如图,在平行四边形中,点,分别在,上,若想要使四边形为平行四边形,需添加一个条件,这个条件不可以是( )
A. B.
C. D.
2.用两个全等的三角形纸片拼成平行四边形,如果三角形的三边互不相等,你能拼出( )种不同的平行四边形.
A. B. C. D.
3.如图,在平行四边形中,,,,分别是,,,的中点,则图中共有平行四边形的个数是( )
A. B. C. D.
4.如图,在中,延长至,使得.过中点作(点位于点右侧),且.连接,若,则的长为( )
A. B. C. D.
5.点,分别是三角形的边,的中点,如图,
求证:且
证明:延长到,使,连接,,,
又,则四边形是平行四边形,
接着以下是排序错误的证明过程;
①;
②;
③四边形是平行四边形;
④且
则正确的证明排序应是:( )
A.②③①④ B.②①③④
C.①③④② D.①③②④
6.如图,在中,,,分别为,,的中点,若四边形的面积为,则四边形的面积为( )
A. B. C. D.
7.在中,,满足下列条件但不一定能构成平行四边形的是( )
A.四个内角的平分线围成的四边形
B.过四个顶点分别作对角线的平行线所围成的四边形
C.以各边中点为顶点的四边形
D.以一条对角线上的两点与另两个顶点组成的四边形
8.如图,两处被池塘隔开,为了测量两处之间的距离,在直线外选一点连接并分别取线段的中点测得则的长为( )
A. B. C. D.
9.如图,在等边三角形中,,射线,点从点出发沿射线以的速度运动,点从点出发沿射线以的速度运动.如果点,同时出发,当以为顶点的四边形是平行四边形时,运动时间的值为( )
A. B. C. D.或
二、填空题(共4小题)
10.如图,在四边形中,连接,.请你添加一个条件 ,使.(填一种情况即可)
11.已知、、是平面内不共线的三个点,如果以、、、四点为顶点的四边形是平行四边形,那么满足条件的点最多有 个.
12.如图所示,点,分别是的边,的中点,连接,过点作,交的延长线于点,若,则的长为 .
13.已知:如图,四边形中,,,,,,分别是边,,,的中点,则四边形的周长是 .
三、解答题(共5小题)
14.如图,在四边形中,,试判断四边形的形状,并说明理由.
15.已知:如图所示,,,,分别是,,,的中点.求证:四边形是平行四边形.
16.如图所示,已知、、分别是各边的中点,求证:与互相平分.
17.如图,在梯形中,,,如果的周长为,,求梯形的周长.
18.已知:如图,在 中,延长至点,延长至点,使得.连接,与对角线交于点. 求证.
参考答案
1.【答案】B
【解析】项,∵四边形是平行四边形,
∴.
∵,
∴四边形是平行四边形.
∴选项不符合题意;
项,根据,可知四边形可能是平行四边形,也有可能是等腰梯形,故选项符合题意;
项,由,,可以推出≌,
∴.
∵,∴.
又∵,
∴四边形是平行四边形.
故选项不符合题意;
项,∵,
∴.
∵,
∴四边形是平行四边形.
故选项不符合题意.
故选
2.【答案】C
3.【答案】C
【解析】∵四边形是平行四边形,
∴,.
∵,,,分别是,,,的中点,
∴,
∴四边形是平行四边形,
同理:四边形是平行四边形,四边形是平行四边形.
故选.
4.【答案】B
【解析】取的中点,连接,
是的中点,
是的中位线,
,
设,则,
,
,
,
四边形是平行四边形,
,
故选:.
5.【答案】A
【解析】四边形是平行四边形,
,
,
四边形是平行四边形,
,且,
,
且
对照题中四个步骤,可得②③①④正确;
故答案选:
6.【答案】C
7.【答案】D
【解析】【分析】
本题主要考查的是平行四边形的判定及性质的有关知识,由题意利用平行四边形的判定及性质对给出的各个选项进行逐一判断即可求解.
【解答】
解:∵的四个内角平分线围成的四边形是平行四边形,
∴选项正确;
∵过四个顶点作对边的高线围成的四边形是平行四边形,
∴选项正确;
∵以各边中点为顶点的四边形是平行四边形,
∴选项正确;
∵以一条对角线上的两点与另两个顶点为顶点的四边形不一定是平行四边形,
∴选项不正确.
故选.
8.【答案】C
9.【答案】D
10.【答案】(答案不唯一)
【解析】添加的条件:,理由是:
,
,
,
四边形是平行四边形,
11.【答案】
【解析】本题主要考查平行四边形的判定方法,掌握平行四边形的判定方法是解题的关键,即①两组对边分别平行,②两组对边分别相等,③一组对边平行且相等,④两组对角分别相等,⑤对角线互相平分的四边形是平行四边形分别过、、三点作直线、、,分别交于点、、,根据平行四边形的判定方法可知、、为满足条件的点.
解:如图,连接、、,分别过、、三点作直线、、,分别交于点、、,
∵,,
∴四边形为平行四边形,
同理可知四边形、四边形也为平行四边形,
故、、三点为满足条件的点,
故答案为.
12.【答案】
【解析】、分别是的边、的中点,
为的中位线,
,,
,
四边形为平行四边形,
,
.
故答案为:.
13.【答案】
【解析】是的中位线,
,同理,,
,
四边形是平行四边形,
四边形的周长.
14.【答案】四边形是平行四边形.
理由:∵,
∴.
∵,
∴,
∴,
∴四边形是平行四边形
【解析】四边形是平行四边形.
理由:∵,
∴.
∵,
∴,
∴,
∴四边形是平行四边形
15.【答案】证明:连接.
,,,分别是,,,的中点,
,,,,
,,
四边形是平行四边形.
16.【答案】因为、分别是、的中点,
所以,.
又,
所以.
所以四边形是平行四边形.
所以与互相平分.
【解析】根据三角形中位线定理和平行四边形的判定定理即可判定四边形是平行四边形,所以与互相平分.
17.【答案】解:,(已知),
四边形是平行四边形(两组对边互相平行的四边形是平行四边形);
,(平行四边形的对边相等),
梯形的周长
的周长
,
即梯形的周长是.
【解析】首先根据平行四边形的判定定理(两组对边互相平行的四边形是平行四边形)证得四边形是平行四边形;然后由平行四边形的对边相等推知,;最后结合的周长来求梯形的周长.
本题主要考查了梯形的解决方法,可以转化为平行四边形的问题与三角形的问题解决.
18.【答案】如图,连接,
在 中,由平行四边形的性质得,且, 又∵,∴++, 即. 又∵,∴四边形是平行四边形, ∴
【解析】如图,连接,
在 中,由平行四边形的性质得,且, 又∵,∴++, 即. 又∵,∴四边形是平行四边形, ∴
学校:______姓名:______班级:______考号:______
一、单选题(共9小题)
1.如图,在平行四边形中,点,分别在,上,若想要使四边形为平行四边形,需添加一个条件,这个条件不可以是( )
A. B.
C. D.
2.用两个全等的三角形纸片拼成平行四边形,如果三角形的三边互不相等,你能拼出( )种不同的平行四边形.
A. B. C. D.
3.如图,在平行四边形中,,,,分别是,,,的中点,则图中共有平行四边形的个数是( )
A. B. C. D.
4.如图,在中,延长至,使得.过中点作(点位于点右侧),且.连接,若,则的长为( )
A. B. C. D.
5.点,分别是三角形的边,的中点,如图,
求证:且
证明:延长到,使,连接,,,
又,则四边形是平行四边形,
接着以下是排序错误的证明过程;
①;
②;
③四边形是平行四边形;
④且
则正确的证明排序应是:( )
A.②③①④ B.②①③④
C.①③④② D.①③②④
6.如图,在中,,,分别为,,的中点,若四边形的面积为,则四边形的面积为( )
A. B. C. D.
7.在中,,满足下列条件但不一定能构成平行四边形的是( )
A.四个内角的平分线围成的四边形
B.过四个顶点分别作对角线的平行线所围成的四边形
C.以各边中点为顶点的四边形
D.以一条对角线上的两点与另两个顶点组成的四边形
8.如图,两处被池塘隔开,为了测量两处之间的距离,在直线外选一点连接并分别取线段的中点测得则的长为( )
A. B. C. D.
9.如图,在等边三角形中,,射线,点从点出发沿射线以的速度运动,点从点出发沿射线以的速度运动.如果点,同时出发,当以为顶点的四边形是平行四边形时,运动时间的值为( )
A. B. C. D.或
二、填空题(共4小题)
10.如图,在四边形中,连接,.请你添加一个条件 ,使.(填一种情况即可)
11.已知、、是平面内不共线的三个点,如果以、、、四点为顶点的四边形是平行四边形,那么满足条件的点最多有 个.
12.如图所示,点,分别是的边,的中点,连接,过点作,交的延长线于点,若,则的长为 .
13.已知:如图,四边形中,,,,,,分别是边,,,的中点,则四边形的周长是 .
三、解答题(共5小题)
14.如图,在四边形中,,试判断四边形的形状,并说明理由.
15.已知:如图所示,,,,分别是,,,的中点.求证:四边形是平行四边形.
16.如图所示,已知、、分别是各边的中点,求证:与互相平分.
17.如图,在梯形中,,,如果的周长为,,求梯形的周长.
18.已知:如图,在 中,延长至点,延长至点,使得.连接,与对角线交于点. 求证.
参考答案
1.【答案】B
【解析】项,∵四边形是平行四边形,
∴.
∵,
∴四边形是平行四边形.
∴选项不符合题意;
项,根据,可知四边形可能是平行四边形,也有可能是等腰梯形,故选项符合题意;
项,由,,可以推出≌,
∴.
∵,∴.
又∵,
∴四边形是平行四边形.
故选项不符合题意;
项,∵,
∴.
∵,
∴四边形是平行四边形.
故选项不符合题意.
故选
2.【答案】C
3.【答案】C
【解析】∵四边形是平行四边形,
∴,.
∵,,,分别是,,,的中点,
∴,
∴四边形是平行四边形,
同理:四边形是平行四边形,四边形是平行四边形.
故选.
4.【答案】B
【解析】取的中点,连接,
是的中点,
是的中位线,
,
设,则,
,
,
,
四边形是平行四边形,
,
故选:.
5.【答案】A
【解析】四边形是平行四边形,
,
,
四边形是平行四边形,
,且,
,
且
对照题中四个步骤,可得②③①④正确;
故答案选:
6.【答案】C
7.【答案】D
【解析】【分析】
本题主要考查的是平行四边形的判定及性质的有关知识,由题意利用平行四边形的判定及性质对给出的各个选项进行逐一判断即可求解.
【解答】
解:∵的四个内角平分线围成的四边形是平行四边形,
∴选项正确;
∵过四个顶点作对边的高线围成的四边形是平行四边形,
∴选项正确;
∵以各边中点为顶点的四边形是平行四边形,
∴选项正确;
∵以一条对角线上的两点与另两个顶点为顶点的四边形不一定是平行四边形,
∴选项不正确.
故选.
8.【答案】C
9.【答案】D
10.【答案】(答案不唯一)
【解析】添加的条件:,理由是:
,
,
,
四边形是平行四边形,
11.【答案】
【解析】本题主要考查平行四边形的判定方法,掌握平行四边形的判定方法是解题的关键,即①两组对边分别平行,②两组对边分别相等,③一组对边平行且相等,④两组对角分别相等,⑤对角线互相平分的四边形是平行四边形分别过、、三点作直线、、,分别交于点、、,根据平行四边形的判定方法可知、、为满足条件的点.
解:如图,连接、、,分别过、、三点作直线、、,分别交于点、、,
∵,,
∴四边形为平行四边形,
同理可知四边形、四边形也为平行四边形,
故、、三点为满足条件的点,
故答案为.
12.【答案】
【解析】、分别是的边、的中点,
为的中位线,
,,
,
四边形为平行四边形,
,
.
故答案为:.
13.【答案】
【解析】是的中位线,
,同理,,
,
四边形是平行四边形,
四边形的周长.
14.【答案】四边形是平行四边形.
理由:∵,
∴.
∵,
∴,
∴,
∴四边形是平行四边形
【解析】四边形是平行四边形.
理由:∵,
∴.
∵,
∴,
∴,
∴四边形是平行四边形
15.【答案】证明:连接.
,,,分别是,,,的中点,
,,,,
,,
四边形是平行四边形.
16.【答案】因为、分别是、的中点,
所以,.
又,
所以.
所以四边形是平行四边形.
所以与互相平分.
【解析】根据三角形中位线定理和平行四边形的判定定理即可判定四边形是平行四边形,所以与互相平分.
17.【答案】解:,(已知),
四边形是平行四边形(两组对边互相平行的四边形是平行四边形);
,(平行四边形的对边相等),
梯形的周长
的周长
,
即梯形的周长是.
【解析】首先根据平行四边形的判定定理(两组对边互相平行的四边形是平行四边形)证得四边形是平行四边形;然后由平行四边形的对边相等推知,;最后结合的周长来求梯形的周长.
本题主要考查了梯形的解决方法,可以转化为平行四边形的问题与三角形的问题解决.
18.【答案】如图,连接,
在 中,由平行四边形的性质得,且, 又∵,∴++, 即. 又∵,∴四边形是平行四边形, ∴
【解析】如图,连接,
在 中,由平行四边形的性质得,且, 又∵,∴++, 即. 又∵,∴四边形是平行四边形, ∴
