19.1.1 变量与函数 同步练习(含解析) 人教版数学 八年级下册
文档属性
| 名称 | 19.1.1 变量与函数 同步练习(含解析) 人教版数学 八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 53.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 00:00:00 | ||
图片预览



文档简介
19.1.1 变量与函数 同步练习 人教版数学 八年级下册
学校:______姓名:______班级:______考号:______
一、单选题(共9小题)
1.设路程为速度为时间为则在关系式中,下列说法正确的是()
A.当一定时是常量是变量 B.当一定时是常量是变量
C.当一定时是常量是变量 D.当一定时是常量是变量
2.在函数中,当时的函数值为,则的值是( )
A. B. C. D.
3.函数y= + 的自变量的取值范围是( )
A.≥ B.≥且 C. D.
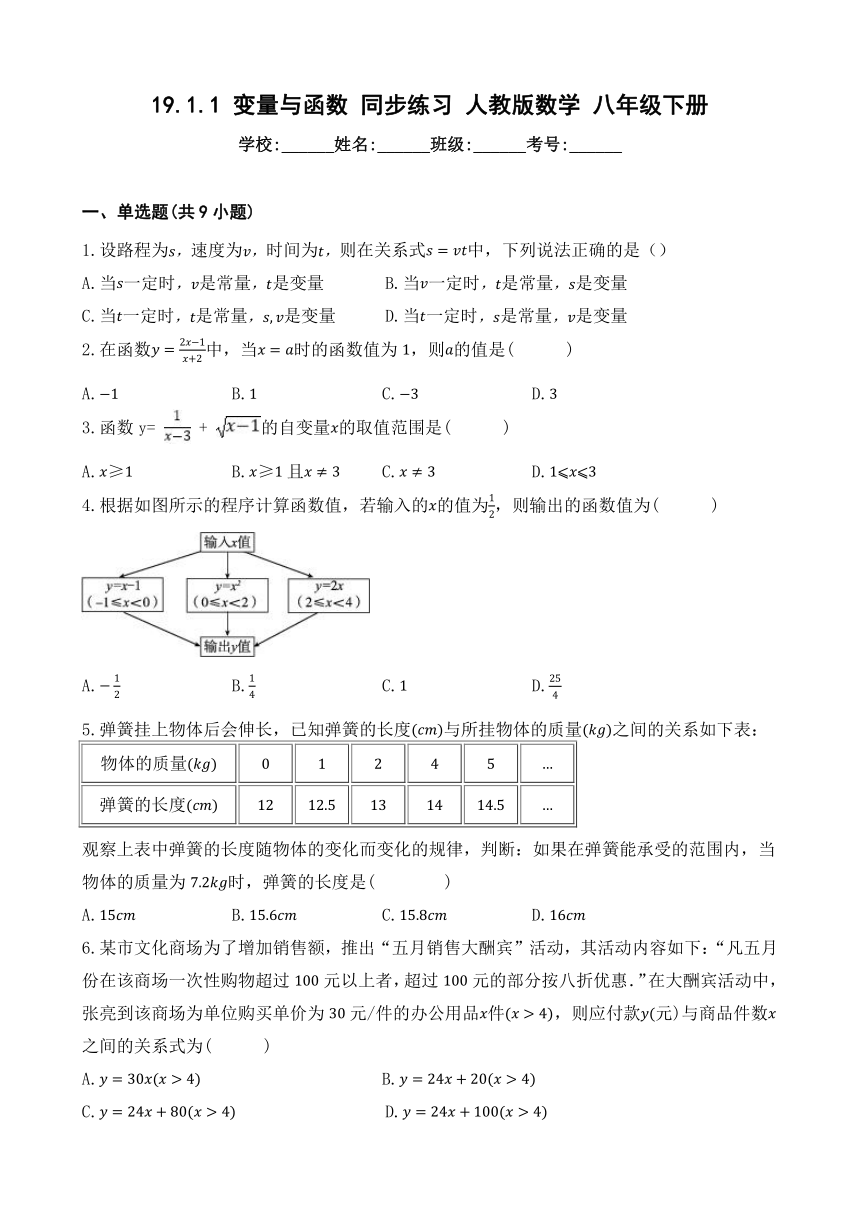
4.根据如图所示的程序计算函数值,若输入的的值为,则输出的函数值为( )
A. B. C. D.
5.弹簧挂上物体后会伸长,已知弹簧的长度与所挂物体的质量之间的关系如下表:
物体的质量
弹簧的长度
观察上表中弹簧的长度随物体的变化而变化的规律,判断:如果在弹簧能承受的范围内,当物体的质量为时,弹簧的长度是( )
A. B. C. D.
6.某市文化商场为了增加销售额,推出“五月销售大酬宾”活动,其活动内容如下:“凡五月份在该商场一次性购物超过元以上者,超过元的部分按八折优惠.”在大酬宾活动中,张亮到该商场为单位购买单价为元/件的办公用品件,则应付款元)与商品件数之间的关系式为( )
A. B.
C. D.
7.用每片长的纸条,重叠粘贴成一条纸带,如图).纸带的长度与纸片的张数之间的函数关系式是( )
A. B. C. D.
8.李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为米,要围成的菜园是如图所示的矩形,设边的长为米,边的长为米,则与之间的函数关系式是( )
A. B.
C. D.
9.若定义如有下列说法:①当时,;②对于正数,均成立;③;④当时,.其中正确的是( )
A.①② B.①③ C.①②④ D.①③④
二、填空题(共8小题)
10.下列各式中:①;②;③;④,是的函数的有 (只填序号).
11.已知在中,设的度数为的度数为则与之间的关系式为 ,其中变量是 ,常量是
12.在弹性限度内,某弹簧伸长的总长度与所挂重物质量之间的关系如下表:
(1)上表反映了 和 两个量之间的关系;
(2)关于与之间的关系式是 .
13.油箱中有油,油从管道中匀速流出,流完,则油箱中剩余油量与流出时间之间的函数关系式是 ,自变量的取值范围是 .
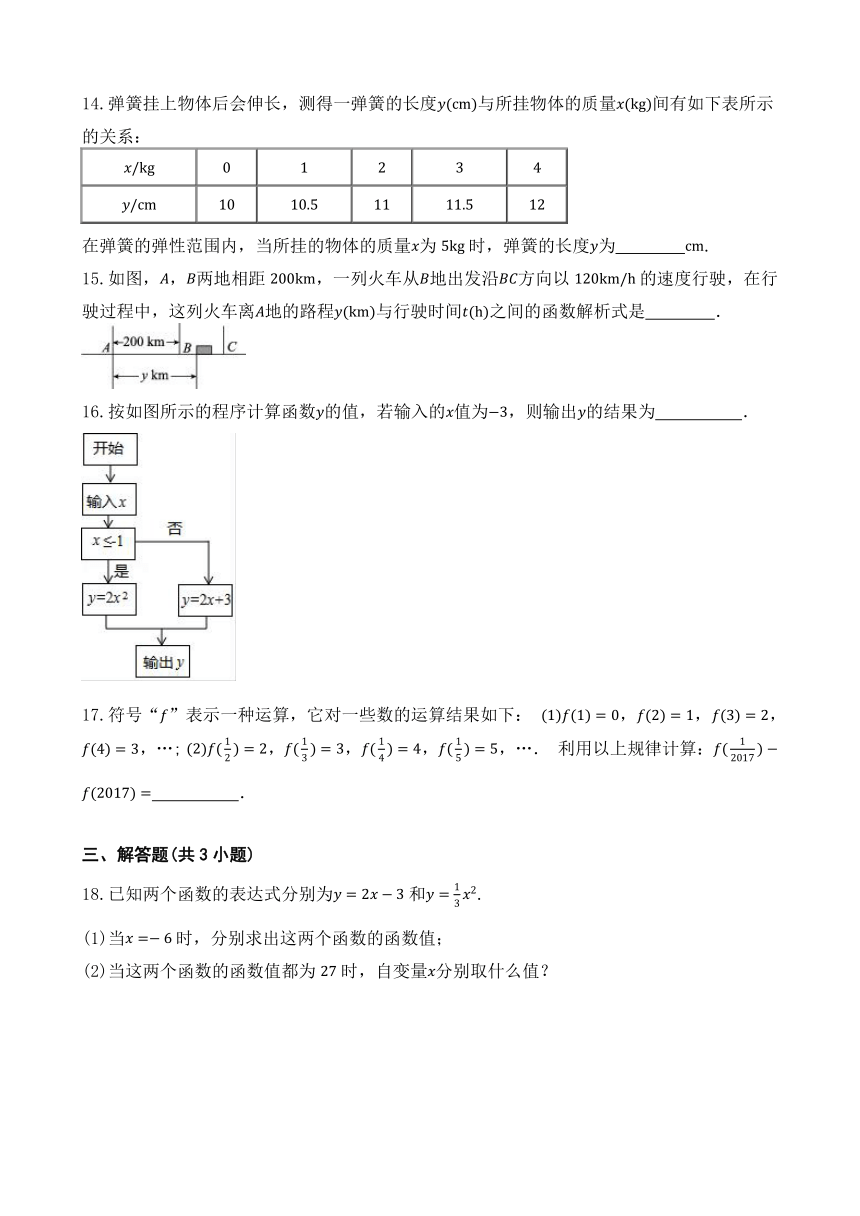
14.弹簧挂上物体后会伸长,测得一弹簧的长度与所挂物体的质量间有如下表所示的关系:
在弹簧的弹性范围内,当所挂的物体的质量为时,弹簧的长度为 .
15.如图,,两地相距,一列火车从地出发沿方向以的速度行驶,在行驶过程中,这列火车离地的路程与行驶时间之间的函数解析式是 .
16.按如图所示的程序计算函数的值,若输入的值为,则输出的结果为 .
17.符号“”表示一种运算,它对一些数的运算结果如下: ,,,,…; ,,,,…. 利用以上规律计算: .
三、解答题(共3小题)
18.已知两个函数的表达式分别为和.
(1)当时,分别求出这两个函数的函数值;
(2)当这两个函数的函数值都为时,自变量分别取什么值?
19.十一期间,小华约同学一起开车到距家千米的景点旅游,出发前,汽车油箱内储油升,当行驶千米时,发现油箱剩余油量为升(假设行驶过程中汽车的耗油量是均匀的).
(1)写出汽车行驶路程(千米)与剩余油量(升)之间的关系式;
(2)若在整个过程中不再加油,求的取值范围
20.如图,中边的长为,边上的高为,当点沿所在直线向点运动时,的面积发生了变化.
(1)指出在这个变化过程中的常量和变量;
(2)若的高为,的面积为,写出与之间的关系式;
(3)当高从变化到时,求的面积的变化范围.
参考答案
1.【答案】C
2.【答案】D
【解析】因为函数中,当时的函数值为 所以所以所以.故选.
3.【答案】B
【解析】由题意,得﹣≥且﹣,
解得≥且,
故选:.
利用函数自变量的取值范围对题目进行判断即可得到答案,需要熟知使函数有意义的自变量的取值的全体,叫做自变量的取值范围.
4.【答案】B
【解析】先根据输入的数值选择关系式,
然后将的值代入相应的关系式进行计算即可.
5.【答案】B
【解析】根据上表中数据得出弹簧的长度与所挂物体的质量之间的函数关系为:,把代入解析式,即可解答.
解:根据表中数据得出弹簧的长度与所挂物体的质量之间的函数关系为:,
把代入解析式,,
故选:.
此题主要考查了函数关系式以及函数值求法,得出正确的函数关系式是解题关键.
6.【答案】B
7.【答案】D
【解析】纸带的长度与纸片的张数之间的函数关系式是.
8.【答案】B
【解析】由题意得,即,
自变量的范围为,故选B
9.【答案】C
【解析】因为所以故①正确;
.
因为
所以故②正确;
,故③错误;
因为,
因为
所以,
所以故④正确.
故选.
10.【答案】①②③
【解析】根据函数的定义可知,满足对于的每一个取值,都有唯一确定的值与之对应的关系,
即可确定函数的个数.
11.【答案】;;
12.【答案】(1)重物质量;弹簧伸长的总长度
(2)
【解析】(1)根据表格可知弹簧伸长的总长度随重物质量的变化而变化.
(2)仔细分析列表可知弹簧伸长的总长度重物质量,因此可列关系式为.
13.【答案】;
【解析】总油量减去剩余油量,得;
剩余油量为非负数,得
解得
时间为非负数,得
即自变量的取值范围是
故答案为
14.【答案】
15.【答案】
【解析】两地相距一列火车从地出发沿方向以的速度行驶,
离地的路程与行驶时间之间的函数表达式是.
故答案为.
16.【答案】.
【解析】,
代入,得,
17.【答案】
18.【答案】(1)把分别代入这两个函数表达式,得
.
(2)把代入函数表达式,可求得
把代入函数表达式,可求得或.
19.【答案】(1)解:该汽车平均每千米的耗油量为(升/千米),所以汽车行驶路程(千米)与剩余油量(升)之间的关系式为.
(2).
20.【答案】(1)∵在变化过程中线段的长度不变,
∴根据常量的定义可知线段的长是常量.
∵点沿所在直线向点运动,
∴的长度在逐渐变短,
∴线段的长是变化的量.
∵高变化,
∴的面积也在变化.
故常量是线段的长,变量为线段的长和的面积
(2)∵的面积,
∴,
∴与之间的关系式为
(3)当时,;
当时,.
∴的面积的变化范围为的面积
【解析】(1)∵在变化过程中线段的长度不变,
∴根据常量的定义可知线段的长是常量.
∵点沿所在直线向点运动,
∴的长度在逐渐变短,
∴线段的长是变化的量.
∵高变化,∴的面积也在变化.
故常量是线段的长,变量为线段的长和的面积
(2)∵的面积,
∴,
∴与之间的关系式为
(3)当时,;
当时,.
∴的面积的变化范围为的面积
学校:______姓名:______班级:______考号:______
一、单选题(共9小题)
1.设路程为速度为时间为则在关系式中,下列说法正确的是()
A.当一定时是常量是变量 B.当一定时是常量是变量
C.当一定时是常量是变量 D.当一定时是常量是变量
2.在函数中,当时的函数值为,则的值是( )
A. B. C. D.
3.函数y= + 的自变量的取值范围是( )
A.≥ B.≥且 C. D.
4.根据如图所示的程序计算函数值,若输入的的值为,则输出的函数值为( )
A. B. C. D.
5.弹簧挂上物体后会伸长,已知弹簧的长度与所挂物体的质量之间的关系如下表:
物体的质量
弹簧的长度
观察上表中弹簧的长度随物体的变化而变化的规律,判断:如果在弹簧能承受的范围内,当物体的质量为时,弹簧的长度是( )
A. B. C. D.
6.某市文化商场为了增加销售额,推出“五月销售大酬宾”活动,其活动内容如下:“凡五月份在该商场一次性购物超过元以上者,超过元的部分按八折优惠.”在大酬宾活动中,张亮到该商场为单位购买单价为元/件的办公用品件,则应付款元)与商品件数之间的关系式为( )
A. B.
C. D.
7.用每片长的纸条,重叠粘贴成一条纸带,如图).纸带的长度与纸片的张数之间的函数关系式是( )
A. B. C. D.
8.李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为米,要围成的菜园是如图所示的矩形,设边的长为米,边的长为米,则与之间的函数关系式是( )
A. B.
C. D.
9.若定义如有下列说法:①当时,;②对于正数,均成立;③;④当时,.其中正确的是( )
A.①② B.①③ C.①②④ D.①③④
二、填空题(共8小题)
10.下列各式中:①;②;③;④,是的函数的有 (只填序号).
11.已知在中,设的度数为的度数为则与之间的关系式为 ,其中变量是 ,常量是
12.在弹性限度内,某弹簧伸长的总长度与所挂重物质量之间的关系如下表:
(1)上表反映了 和 两个量之间的关系;
(2)关于与之间的关系式是 .
13.油箱中有油,油从管道中匀速流出,流完,则油箱中剩余油量与流出时间之间的函数关系式是 ,自变量的取值范围是 .
14.弹簧挂上物体后会伸长,测得一弹簧的长度与所挂物体的质量间有如下表所示的关系:
在弹簧的弹性范围内,当所挂的物体的质量为时,弹簧的长度为 .
15.如图,,两地相距,一列火车从地出发沿方向以的速度行驶,在行驶过程中,这列火车离地的路程与行驶时间之间的函数解析式是 .
16.按如图所示的程序计算函数的值,若输入的值为,则输出的结果为 .
17.符号“”表示一种运算,它对一些数的运算结果如下: ,,,,…; ,,,,…. 利用以上规律计算: .
三、解答题(共3小题)
18.已知两个函数的表达式分别为和.
(1)当时,分别求出这两个函数的函数值;
(2)当这两个函数的函数值都为时,自变量分别取什么值?
19.十一期间,小华约同学一起开车到距家千米的景点旅游,出发前,汽车油箱内储油升,当行驶千米时,发现油箱剩余油量为升(假设行驶过程中汽车的耗油量是均匀的).
(1)写出汽车行驶路程(千米)与剩余油量(升)之间的关系式;
(2)若在整个过程中不再加油,求的取值范围
20.如图,中边的长为,边上的高为,当点沿所在直线向点运动时,的面积发生了变化.
(1)指出在这个变化过程中的常量和变量;
(2)若的高为,的面积为,写出与之间的关系式;
(3)当高从变化到时,求的面积的变化范围.
参考答案
1.【答案】C
2.【答案】D
【解析】因为函数中,当时的函数值为 所以所以所以.故选.
3.【答案】B
【解析】由题意,得﹣≥且﹣,
解得≥且,
故选:.
利用函数自变量的取值范围对题目进行判断即可得到答案,需要熟知使函数有意义的自变量的取值的全体,叫做自变量的取值范围.
4.【答案】B
【解析】先根据输入的数值选择关系式,
然后将的值代入相应的关系式进行计算即可.
5.【答案】B
【解析】根据上表中数据得出弹簧的长度与所挂物体的质量之间的函数关系为:,把代入解析式,即可解答.
解:根据表中数据得出弹簧的长度与所挂物体的质量之间的函数关系为:,
把代入解析式,,
故选:.
此题主要考查了函数关系式以及函数值求法,得出正确的函数关系式是解题关键.
6.【答案】B
7.【答案】D
【解析】纸带的长度与纸片的张数之间的函数关系式是.
8.【答案】B
【解析】由题意得,即,
自变量的范围为,故选B
9.【答案】C
【解析】因为所以故①正确;
.
因为
所以故②正确;
,故③错误;
因为,
因为
所以,
所以故④正确.
故选.
10.【答案】①②③
【解析】根据函数的定义可知,满足对于的每一个取值,都有唯一确定的值与之对应的关系,
即可确定函数的个数.
11.【答案】;;
12.【答案】(1)重物质量;弹簧伸长的总长度
(2)
【解析】(1)根据表格可知弹簧伸长的总长度随重物质量的变化而变化.
(2)仔细分析列表可知弹簧伸长的总长度重物质量,因此可列关系式为.
13.【答案】;
【解析】总油量减去剩余油量,得;
剩余油量为非负数,得
解得
时间为非负数,得
即自变量的取值范围是
故答案为
14.【答案】
15.【答案】
【解析】两地相距一列火车从地出发沿方向以的速度行驶,
离地的路程与行驶时间之间的函数表达式是.
故答案为.
16.【答案】.
【解析】,
代入,得,
17.【答案】
18.【答案】(1)把分别代入这两个函数表达式,得
.
(2)把代入函数表达式,可求得
把代入函数表达式,可求得或.
19.【答案】(1)解:该汽车平均每千米的耗油量为(升/千米),所以汽车行驶路程(千米)与剩余油量(升)之间的关系式为.
(2).
20.【答案】(1)∵在变化过程中线段的长度不变,
∴根据常量的定义可知线段的长是常量.
∵点沿所在直线向点运动,
∴的长度在逐渐变短,
∴线段的长是变化的量.
∵高变化,
∴的面积也在变化.
故常量是线段的长,变量为线段的长和的面积
(2)∵的面积,
∴,
∴与之间的关系式为
(3)当时,;
当时,.
∴的面积的变化范围为的面积
【解析】(1)∵在变化过程中线段的长度不变,
∴根据常量的定义可知线段的长是常量.
∵点沿所在直线向点运动,
∴的长度在逐渐变短,
∴线段的长是变化的量.
∵高变化,∴的面积也在变化.
故常量是线段的长,变量为线段的长和的面积
(2)∵的面积,
∴,
∴与之间的关系式为
(3)当时,;
当时,.
∴的面积的变化范围为的面积
