19.1.2 函数的图象 同步练习(含解析) 人教版数学八年级下册
文档属性
| 名称 | 19.1.2 函数的图象 同步练习(含解析) 人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 191.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 14:29:20 | ||
图片预览



文档简介
19.1.2 函数的图象 同步练习 人教版数学 八年级下册
学校:______姓名:______班级:______考号:______
一、单选题(共10小题)
1.~个月的婴儿生长发育得非常快,出生体重为克的婴儿,他们的体重(克)和月龄(月)之间的关系如下表所示,则个月大的婴儿的体重为( )
A.克 B.克 C.克 D.克
2.一个蓄水池有水,打开放水闸门放水,水池里的水量和放水时间的关系如下表:
放水时间 …
水池里的水量 …
下面说法不正确的是( )
A.水池里的水量是自变量,放水时间是因变量
B.每分钟放水
C.放水后,水池里还有水
D.放水后,水池里的水全部放完
3.爷爷在离家米的公园锻炼后回家,离开公园分钟后,爷爷停下来与朋友聊天分钟,接着又走了分钟回到家中.下面图形中表示爷爷离家的距离(米)与爷爷离开公园的时间(分)之间的函数关系是( )
A. B.
C. D.
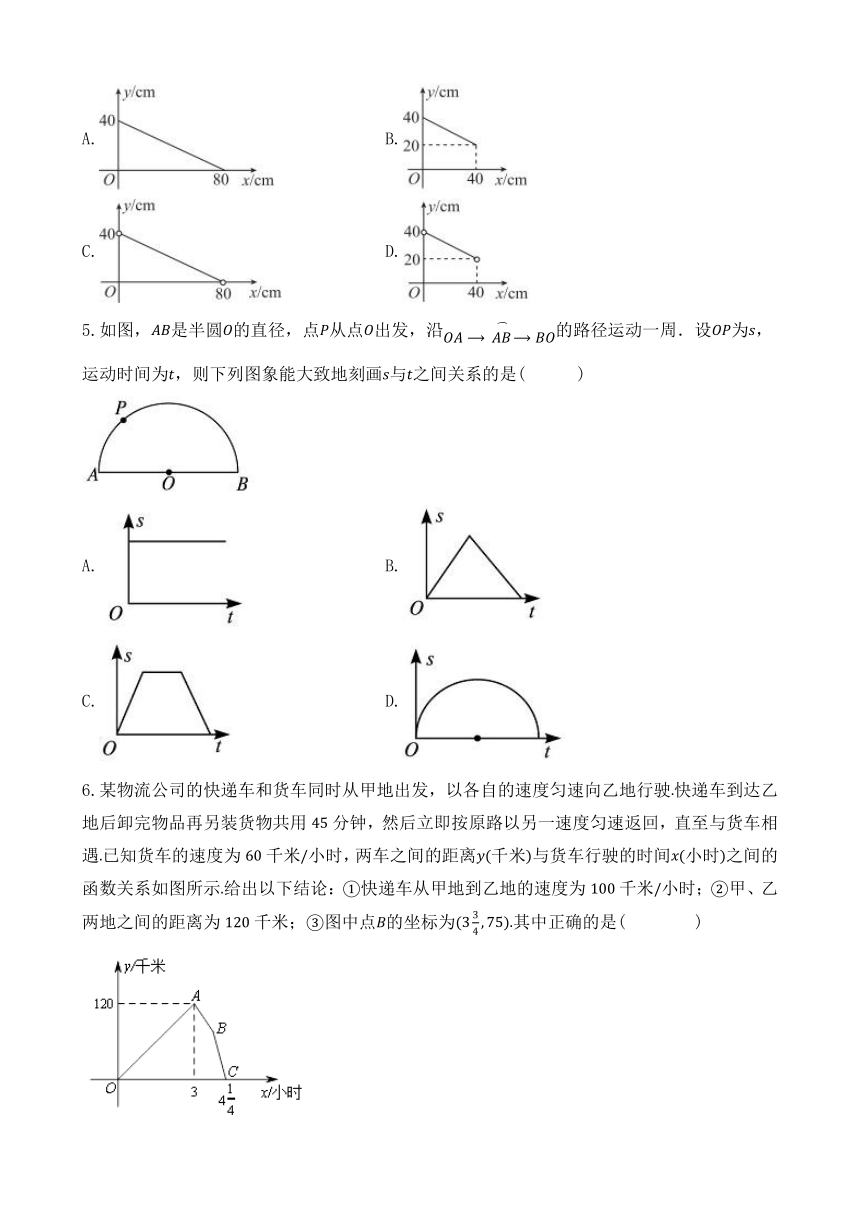
4.若等腰三角形的周长是,则能反映这个等腰三角形的腰长与底边长的函数关系的图象是( )
A. B.
C. D.
5.如图,是半圆的直径,点从点出发,沿的路径运动一周.设为,运动时间为,则下列图象能大致地刻画与之间关系的是( )
A. B.
C. D.
6.某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶快递车到达乙地后卸完物品再另装货物共用分钟,然后立即按原路以另一速度匀速返回,直至与货车相遇已知货车的速度为千米小时,两车之间的距离千米与货车行驶的时间小时之间的函数关系如图所示给出以下结论:快递车从甲地到乙地的速度为千米小时;甲、乙两地之间的距离为千米;图中点的坐标为其中正确的是( )
A. B. C. D.
7.小阳在如图①的扇形舞台上沿匀速行走,他从点出发,沿箭头所示的方向经过点再走到点,共用时秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走路的时间为(单位:秒),他与摄像机的距离为(单位:米),表示与的函数关系的图象大致如图②,则这个固定位置可能是图①中的( )
A.点 B.点 C.点 D.点
8.某快递公司每天上午:~:为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量(件)与时间(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A.: B.: C.: D.:
9.将矩形纸板剪掉一个小矩形后剩余部分如图所示,动点从点出发,沿路径匀速运动,速度为,点到达终点后停止运动,的面积与点运动的时间的关系如图所示,根据图象获取了以下的信息:
①;
②;
③点从点运动到点需要;
④矩形纸板裁剪前后周长均为.
其中正确信息个数有( )
A.个 B.个 C.个 D.个
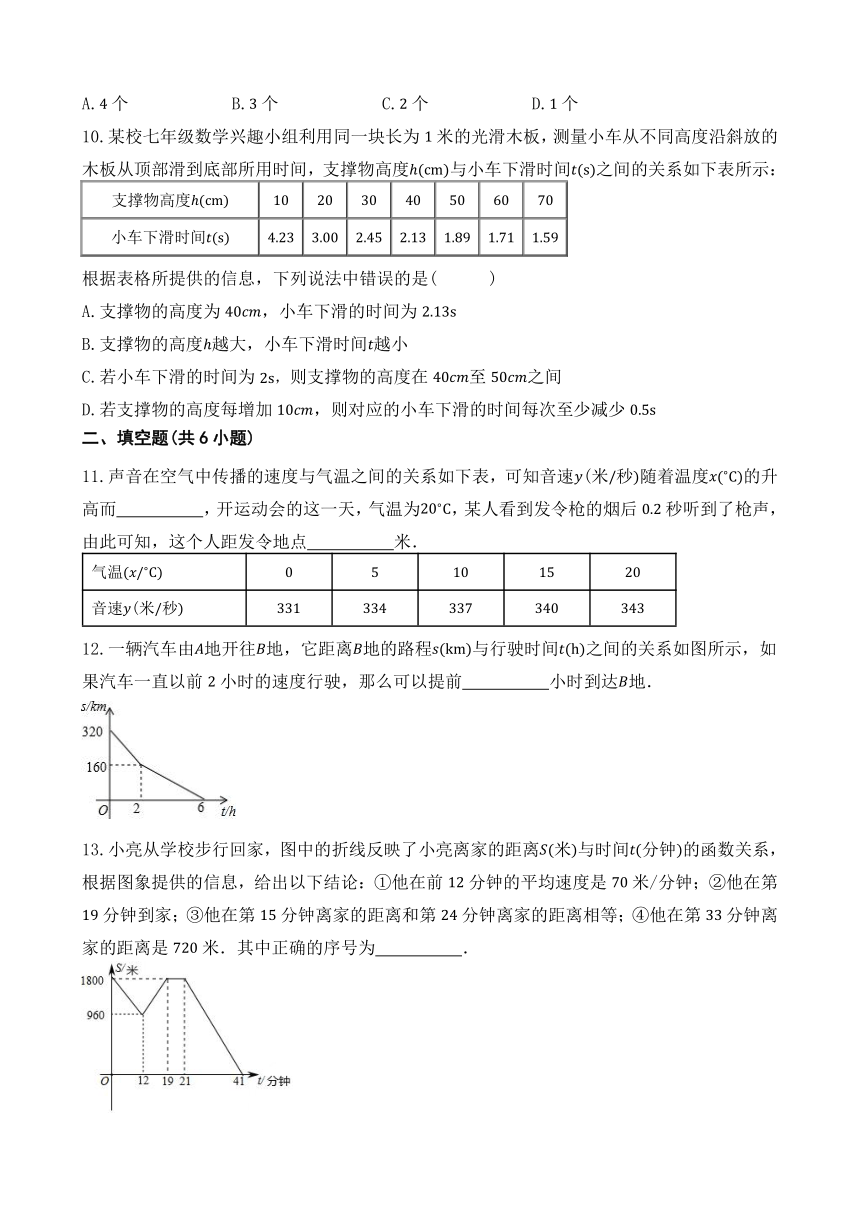
10.某校七年级数学兴趣小组利用同一块长为米的光滑木板,测量小车从不同高度沿斜放的木板从顶部滑到底部所用时间,支撑物高度与小车下滑时间之间的关系如下表所示:
支撑物高度
小车下滑时间
根据表格所提供的信息,下列说法中错误的是( )
A.支撑物的高度为,小车下滑的时间为
B.支撑物的高度越大,小车下滑时间越小
C.若小车下滑的时间为则支撑物的高度在至之间
D.若支撑物的高度每增加,则对应的小车下滑的时间每次至少减少
二、填空题(共6小题)
11.声音在空气中传播的速度与气温之间的关系如下表,可知音速(米秒随着温度的升高而 ,开运动会的这一天,气温为,某人看到发令枪的烟后秒听到了枪声,由此可知,这个人距发令地点 米.
气温
音速(米秒
12.一辆汽车由地开往地,它距离地的路程与行驶时间之间的关系如图所示,如果汽车一直以前小时的速度行驶,那么可以提前 小时到达地.
13.小亮从学校步行回家,图中的折线反映了小亮离家的距离米与时间分钟的函数关系,根据图象提供的信息,给出以下结论:①他在前分钟的平均速度是米/分钟;②他在第分钟到家;③他在第分钟离家的距离和第分钟离家的距离相等;④他在第分钟离家的距离是米.其中正确的序号为 .
14.如图①,在长方形中,动点从点出发,沿→→→运动至点停止,设点的运动路程为三角形的面积为如果关于的函数图象如图②所示,那么长方形的周长是 .
15.如图所示,在中是边上的动点,且点从点向点运动.若设的面积为,则与之间的关系式为 .(不必写的取值范围)
16.某医药研究院试验一种新药药效时发现,成人如果按规定剂量服用,每毫升血液中含药量(微克)随时间(时)的变化情况如图所示.如果每毫升血液中含药量达到微克以上(含微克)时治疗疾病为有效,那么有效时长是 小时.
三、解答题(共4小题)
17.通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量与函数值的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
… …
… …
(1)当 时,;
(2)根据表中数值描点,并画出函数图象;
(3)观察画出的图象,写出这个函数的一条性质:
18.小明家所在地的供电公司实行“峰谷电价”,峰时::电价为元/度,谷时::电价为元/度.为了解空调制暖的耗能情况,小明记录了家里某天时时内空调制暖的用电量,其用电量(度)与时间(时)的函数关系如图所示.
(1)小明家白天不开空调的时间共 ;
(2)求小明家该天空调制暖所用的电费;
(3)设空调制暖所用电费为元,请画出该天时时内与之间的函数图象.(标注必要数据)
19.甲、乙两车从城出发前往城,在整个行程中,两车离开城的路程(千米)与时刻的对应关系如图所示.
(1),两城之间的距离是多少千米?
(2)求乙车出发多长时间追上甲车.
20.如图,,,为上的定点.连接,,为上的一个动点,连接,将射线绕点顺时针旋转,交于点,连接.若,,记,两点间距离为,,两点间的距离为.
小东根据学习函数的经验,对函数随自变量的变化而变化的规律进行了探究.下面是小东探究的过程,请补充完整:
(1)通过取点、画图、测量,得到了与的几组值,如下表,补全表格:
(2)在平面直角坐标系中,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当时,的长度约为 .
参考答案
1.【答案】C
2.【答案】A
3.【答案】B
【解析】由题意,爷爷在公园回家,则当时,;
从公园回家一共用了分钟,则当时,;
结合选项可知答案.
故选:.
4.【答案】D
【解析】函数的关系式为,
其中的取值范围为 ,
故选D
5.【答案】C
【解析】当点从点向点运动,逐渐增大,当点从点向点运动,不变,当点从点向点运动,逐渐减小,故能大致地刻画与之间关系的是C.
故选C.
6.【答案】C
【解析】【分析】
本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题,关键是根据一次函数的性质和图象结合实际问题判断出每一结论是否正确要解答本题需要熟悉一次函数的图象特征,再根据一次函数的性质和图象结合实际问题对每一项进行分析即可得出答案.
【解答】
解:设快递车从甲地到乙地的速度为千米时,则
,
.
故正确;
因为千米是快递车到达乙地后两车之间的距离,不是甲、乙两地之间的距离,
故错误;
因为快递车到达乙地后缷完物品再另装货物共用分钟,
所以图中点的横坐标为,
纵坐标为,故正确.
故选.
7.【答案】B
8.【答案】B
9.【答案】C
【解析】由矩形及点 运动过程可知:
时, 点 位于点处,,
则, ,
, ①正确;
时,点位于点处, ,
, ,
, 故运动时间为, 所以③正确;
,
,
时, 点位于点处,
, 所以②错误;
周长 , 所以④错误;
故①③正确, 正确得有 个,
故选 .
本题考查动点面积计算问题, 能够在不同位置清晰计算面积及结合图表确认拐点位置是解题的关键.
利用图表信息结合 面积及逐个运动阶段得到计算数据, 逐个判断正误即可.
10.【答案】D
11.【答案】加快
;
【解析】【分析】 根据表中数据可知:速度与气温之间的关系,还可列出音速与时间的关系式,进而求出答案.
【解答】
观察表中的数据可知,音速随温度的升高而加快;
当气温为时,音速为米秒,而该人是看到发令枪的烟秒后,听到了枪声,则由此可知:这个人距发令地点米.
故填加快;.
12.【答案】
【解析】,,,.
13.【答案】①④
【解析】解:由图象知,前分中的平均速度为:米/分,
故①正确;
由图象知,小亮第分中又返回学校,
故②错误;
小亮在返回学校时的速度为:米/分),
第分离家距离:,
从分到分小亮的速度为:米/分),
第分离家距离:米),
,
故③错误;
小亮在分离家距离:米),
故④正确,
故答案为:①④.
14.【答案】
15.【答案】;略
16.【答案】
【解析】由题意,得当时或
所以有效时长是(时)
故填.
17.【答案】(1)
(2)解:如图:
(3)函数值随的增大而减小(答案不唯一)
18.【答案】(1)
(2)由题意,得时时每小时用电量为(度),时~时每小时用电量为(度),峰时所用电费为(元),谷时所用电费为(元),小明家该天空调制暖所用的电费为(元).
(3)根据题意,可得该天时时内与之间的函数图象如下:
19.【答案】(1)解:由图象可知,两城之间的距离是千米.
(2)设乙车出发小时追上甲车, 由图象可知甲车的速度(千米/时), 乙车的速度(千米/时), 由题意得方程, 解得. 故乙车出发小时追上甲车.
20.【答案】(1)
(2)描点即可;图象如下图所示:当时,测量得:;
(3) 或
【解析】(1)描出后图象后,时,测得(答案不唯一,故答案是;
(2)描点即可;
(3)当时,,即图中点、的位置,从图中测量可得:,,故答案为:或(本题答案不唯一
学校:______姓名:______班级:______考号:______
一、单选题(共10小题)
1.~个月的婴儿生长发育得非常快,出生体重为克的婴儿,他们的体重(克)和月龄(月)之间的关系如下表所示,则个月大的婴儿的体重为( )
A.克 B.克 C.克 D.克
2.一个蓄水池有水,打开放水闸门放水,水池里的水量和放水时间的关系如下表:
放水时间 …
水池里的水量 …
下面说法不正确的是( )
A.水池里的水量是自变量,放水时间是因变量
B.每分钟放水
C.放水后,水池里还有水
D.放水后,水池里的水全部放完
3.爷爷在离家米的公园锻炼后回家,离开公园分钟后,爷爷停下来与朋友聊天分钟,接着又走了分钟回到家中.下面图形中表示爷爷离家的距离(米)与爷爷离开公园的时间(分)之间的函数关系是( )
A. B.
C. D.
4.若等腰三角形的周长是,则能反映这个等腰三角形的腰长与底边长的函数关系的图象是( )
A. B.
C. D.
5.如图,是半圆的直径,点从点出发,沿的路径运动一周.设为,运动时间为,则下列图象能大致地刻画与之间关系的是( )
A. B.
C. D.
6.某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶快递车到达乙地后卸完物品再另装货物共用分钟,然后立即按原路以另一速度匀速返回,直至与货车相遇已知货车的速度为千米小时,两车之间的距离千米与货车行驶的时间小时之间的函数关系如图所示给出以下结论:快递车从甲地到乙地的速度为千米小时;甲、乙两地之间的距离为千米;图中点的坐标为其中正确的是( )
A. B. C. D.
7.小阳在如图①的扇形舞台上沿匀速行走,他从点出发,沿箭头所示的方向经过点再走到点,共用时秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走路的时间为(单位:秒),他与摄像机的距离为(单位:米),表示与的函数关系的图象大致如图②,则这个固定位置可能是图①中的( )
A.点 B.点 C.点 D.点
8.某快递公司每天上午:~:为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量(件)与时间(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A.: B.: C.: D.:
9.将矩形纸板剪掉一个小矩形后剩余部分如图所示,动点从点出发,沿路径匀速运动,速度为,点到达终点后停止运动,的面积与点运动的时间的关系如图所示,根据图象获取了以下的信息:
①;
②;
③点从点运动到点需要;
④矩形纸板裁剪前后周长均为.
其中正确信息个数有( )
A.个 B.个 C.个 D.个
10.某校七年级数学兴趣小组利用同一块长为米的光滑木板,测量小车从不同高度沿斜放的木板从顶部滑到底部所用时间,支撑物高度与小车下滑时间之间的关系如下表所示:
支撑物高度
小车下滑时间
根据表格所提供的信息,下列说法中错误的是( )
A.支撑物的高度为,小车下滑的时间为
B.支撑物的高度越大,小车下滑时间越小
C.若小车下滑的时间为则支撑物的高度在至之间
D.若支撑物的高度每增加,则对应的小车下滑的时间每次至少减少
二、填空题(共6小题)
11.声音在空气中传播的速度与气温之间的关系如下表,可知音速(米秒随着温度的升高而 ,开运动会的这一天,气温为,某人看到发令枪的烟后秒听到了枪声,由此可知,这个人距发令地点 米.
气温
音速(米秒
12.一辆汽车由地开往地,它距离地的路程与行驶时间之间的关系如图所示,如果汽车一直以前小时的速度行驶,那么可以提前 小时到达地.
13.小亮从学校步行回家,图中的折线反映了小亮离家的距离米与时间分钟的函数关系,根据图象提供的信息,给出以下结论:①他在前分钟的平均速度是米/分钟;②他在第分钟到家;③他在第分钟离家的距离和第分钟离家的距离相等;④他在第分钟离家的距离是米.其中正确的序号为 .
14.如图①,在长方形中,动点从点出发,沿→→→运动至点停止,设点的运动路程为三角形的面积为如果关于的函数图象如图②所示,那么长方形的周长是 .
15.如图所示,在中是边上的动点,且点从点向点运动.若设的面积为,则与之间的关系式为 .(不必写的取值范围)
16.某医药研究院试验一种新药药效时发现,成人如果按规定剂量服用,每毫升血液中含药量(微克)随时间(时)的变化情况如图所示.如果每毫升血液中含药量达到微克以上(含微克)时治疗疾病为有效,那么有效时长是 小时.
三、解答题(共4小题)
17.通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量与函数值的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
… …
… …
(1)当 时,;
(2)根据表中数值描点,并画出函数图象;
(3)观察画出的图象,写出这个函数的一条性质:
18.小明家所在地的供电公司实行“峰谷电价”,峰时::电价为元/度,谷时::电价为元/度.为了解空调制暖的耗能情况,小明记录了家里某天时时内空调制暖的用电量,其用电量(度)与时间(时)的函数关系如图所示.
(1)小明家白天不开空调的时间共 ;
(2)求小明家该天空调制暖所用的电费;
(3)设空调制暖所用电费为元,请画出该天时时内与之间的函数图象.(标注必要数据)
19.甲、乙两车从城出发前往城,在整个行程中,两车离开城的路程(千米)与时刻的对应关系如图所示.
(1),两城之间的距离是多少千米?
(2)求乙车出发多长时间追上甲车.
20.如图,,,为上的定点.连接,,为上的一个动点,连接,将射线绕点顺时针旋转,交于点,连接.若,,记,两点间距离为,,两点间的距离为.
小东根据学习函数的经验,对函数随自变量的变化而变化的规律进行了探究.下面是小东探究的过程,请补充完整:
(1)通过取点、画图、测量,得到了与的几组值,如下表,补全表格:
(2)在平面直角坐标系中,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当时,的长度约为 .
参考答案
1.【答案】C
2.【答案】A
3.【答案】B
【解析】由题意,爷爷在公园回家,则当时,;
从公园回家一共用了分钟,则当时,;
结合选项可知答案.
故选:.
4.【答案】D
【解析】函数的关系式为,
其中的取值范围为 ,
故选D
5.【答案】C
【解析】当点从点向点运动,逐渐增大,当点从点向点运动,不变,当点从点向点运动,逐渐减小,故能大致地刻画与之间关系的是C.
故选C.
6.【答案】C
【解析】【分析】
本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题,关键是根据一次函数的性质和图象结合实际问题判断出每一结论是否正确要解答本题需要熟悉一次函数的图象特征,再根据一次函数的性质和图象结合实际问题对每一项进行分析即可得出答案.
【解答】
解:设快递车从甲地到乙地的速度为千米时,则
,
.
故正确;
因为千米是快递车到达乙地后两车之间的距离,不是甲、乙两地之间的距离,
故错误;
因为快递车到达乙地后缷完物品再另装货物共用分钟,
所以图中点的横坐标为,
纵坐标为,故正确.
故选.
7.【答案】B
8.【答案】B
9.【答案】C
【解析】由矩形及点 运动过程可知:
时, 点 位于点处,,
则, ,
, ①正确;
时,点位于点处, ,
, ,
, 故运动时间为, 所以③正确;
,
,
时, 点位于点处,
, 所以②错误;
周长 , 所以④错误;
故①③正确, 正确得有 个,
故选 .
本题考查动点面积计算问题, 能够在不同位置清晰计算面积及结合图表确认拐点位置是解题的关键.
利用图表信息结合 面积及逐个运动阶段得到计算数据, 逐个判断正误即可.
10.【答案】D
11.【答案】加快
;
【解析】【分析】 根据表中数据可知:速度与气温之间的关系,还可列出音速与时间的关系式,进而求出答案.
【解答】
观察表中的数据可知,音速随温度的升高而加快;
当气温为时,音速为米秒,而该人是看到发令枪的烟秒后,听到了枪声,则由此可知:这个人距发令地点米.
故填加快;.
12.【答案】
【解析】,,,.
13.【答案】①④
【解析】解:由图象知,前分中的平均速度为:米/分,
故①正确;
由图象知,小亮第分中又返回学校,
故②错误;
小亮在返回学校时的速度为:米/分),
第分离家距离:,
从分到分小亮的速度为:米/分),
第分离家距离:米),
,
故③错误;
小亮在分离家距离:米),
故④正确,
故答案为:①④.
14.【答案】
15.【答案】;略
16.【答案】
【解析】由题意,得当时或
所以有效时长是(时)
故填.
17.【答案】(1)
(2)解:如图:
(3)函数值随的增大而减小(答案不唯一)
18.【答案】(1)
(2)由题意,得时时每小时用电量为(度),时~时每小时用电量为(度),峰时所用电费为(元),谷时所用电费为(元),小明家该天空调制暖所用的电费为(元).
(3)根据题意,可得该天时时内与之间的函数图象如下:
19.【答案】(1)解:由图象可知,两城之间的距离是千米.
(2)设乙车出发小时追上甲车, 由图象可知甲车的速度(千米/时), 乙车的速度(千米/时), 由题意得方程, 解得. 故乙车出发小时追上甲车.
20.【答案】(1)
(2)描点即可;图象如下图所示:当时,测量得:;
(3) 或
【解析】(1)描出后图象后,时,测得(答案不唯一,故答案是;
(2)描点即可;
(3)当时,,即图中点、的位置,从图中测量可得:,,故答案为:或(本题答案不唯一
