四川省成都市第七中学2023-2024学年高二下学期3月阶段性检测数学试题(PDF版,含答案)
文档属性
| 名称 | 四川省成都市第七中学2023-2024学年高二下学期3月阶段性检测数学试题(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 11:25:30 | ||
图片预览



文档简介
2023-2024学年度高二下期3月阶段性检测
数学试题
(考试时间:120分钟:满分:150分)
注意事项:
1本试卷分第〡卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、班级、座号、
准考证号填写在答题卡上.
2回答第〡卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用
橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.
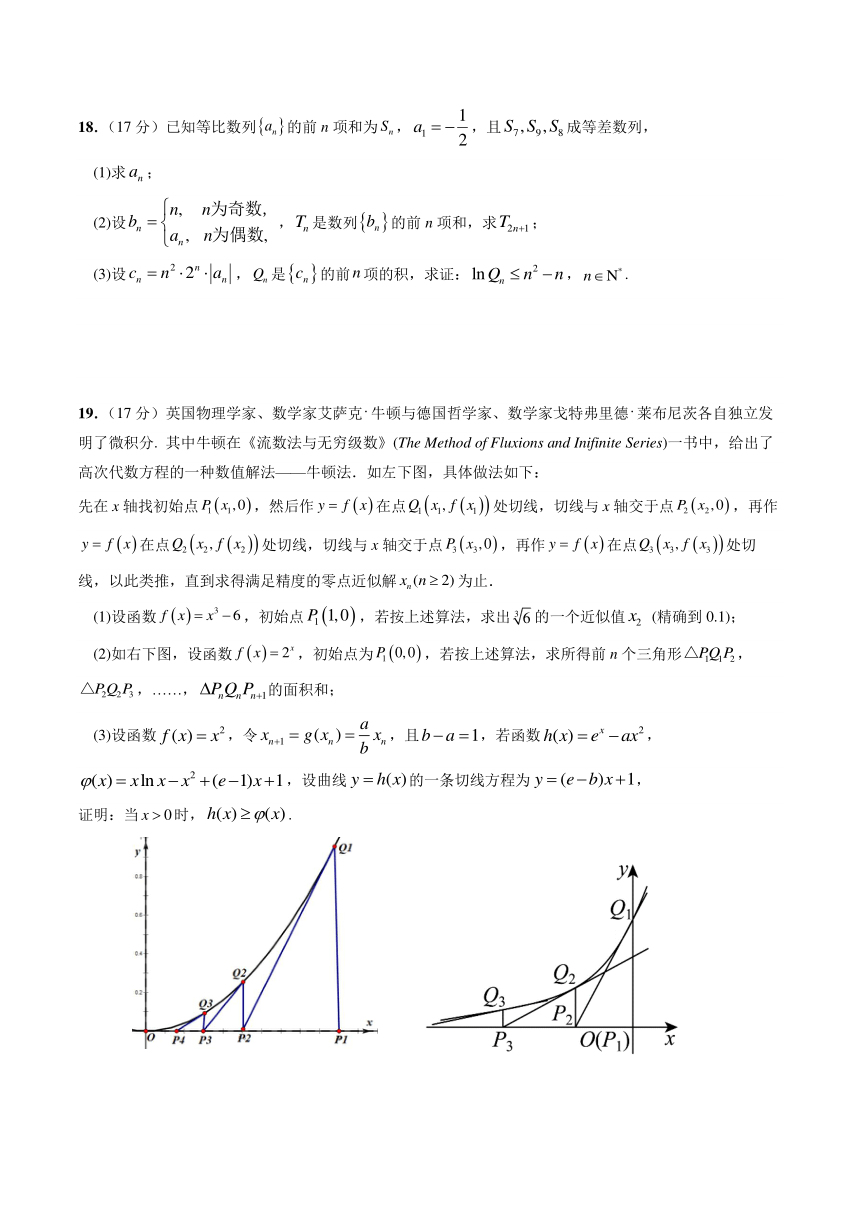
3回答第卷时,将答案写在答题卡上,写在本试卷上无效.
4,考试结束后,请考生个人留存试卷并将答题卡交回给监考教师
第1卷(选择题,共58分)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合
要求的.
口:在等比数列a}中,a=2,a-7,则公比9=(
A月
c.
D2
2.函数f(X)=2x+sin×在区间[0,π]上的()
A.最小值为0,最大值为π+1
B.最小值为0,最大值为2π
C.最小值为+1,最大值为2π
D.最小值为0,最大值为2
3.在数别{a}中,若4=-1,4=1n≥2),则a=()
A.2
B.-1
c.
D.1
4.如图,向一个半球形的水池注水时,向池子注水速度不变(即单位时间内注入水量
相同),若池子中水的高度h是关于时间t的函数h(t),则函数h(t)的图象可能是()
hk
ho----
C
o
A.
B
D
to
to
5.某个体户计划同时销售A,B两种商品,当投资额为x(×>0)千元时,在销售A,B商品中所获收益分
别为f(x)千元与g(x)千元,其中f(x)=2×,g(x)=4I(2x+1),如果该个体户准备共投入5千元销售
A,B两种商品,为使总收益最大,则B商品需投()千元
A
c.
D.
6.已知函数满足f(x)=f(2)e-f(o)x+2,则)的单讽递塔区间为()
4.(-,0)
B.(1,十o)
C.(-x,1)
D.(0,+)
7.若咽数f广inx+)xx在
3
上怡有2个极俏点,则实数a的取俏范围是()
2
B.
2引
c.〔89)
8.在数列{u}巾,Sn为共前n项,首项4,=1,又函数f(x)-x-.1si血x+(2n+)x+1,若f"(0)=0,
则S24()
4.22023-2024B.22-2025.202-2026D.22026-2027
二、多项选择题:本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有多项符合题目
的要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.定义:设f”(x)是(x)的导的数,”()是函数'(x)的导数,若方程"(x)=0有实数解x,则称点
(xf(》为函数y=()的拐点”.经过深究发见:任一个三次函数都有拐点”且拐点”就是三次函数
中心.已知函数()=以+x+〔b≠0)的对称巾心为,1),则下列说法巾正伯的
B.函数八)既有极大值叉有极小值
C.函数f(x)有个零点
D.过(-1,宁可以作三条占线与y=f图象相切
10.已函数f)=-1弓,则下列若论止确韵是()
A.f(x)的单调递增区间是0,,(山,+)
3.f(x)的值域为R
C.f(log22024)+.f(10g22023)=1
D若o)g-6,e(Q).ca+o小,则e=l
11.已知数列}满足4=1,+1=-,n∈N,则()
4.{a}足递诚数列
B.a.>h(n>2)
C.a024≤202x
1
1
…女
4.114.114,/1s
D.
数学试题
(考试时间:120分钟:满分:150分)
注意事项:
1本试卷分第〡卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、班级、座号、
准考证号填写在答题卡上.
2回答第〡卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用
橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.
3回答第卷时,将答案写在答题卡上,写在本试卷上无效.
4,考试结束后,请考生个人留存试卷并将答题卡交回给监考教师
第1卷(选择题,共58分)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合
要求的.
口:在等比数列a}中,a=2,a-7,则公比9=(
A月
c.
D2
2.函数f(X)=2x+sin×在区间[0,π]上的()
A.最小值为0,最大值为π+1
B.最小值为0,最大值为2π
C.最小值为+1,最大值为2π
D.最小值为0,最大值为2
3.在数别{a}中,若4=-1,4=1n≥2),则a=()
A.2
B.-1
c.
D.1
4.如图,向一个半球形的水池注水时,向池子注水速度不变(即单位时间内注入水量
相同),若池子中水的高度h是关于时间t的函数h(t),则函数h(t)的图象可能是()
hk
ho----
C
o
A.
B
D
to
to
5.某个体户计划同时销售A,B两种商品,当投资额为x(×>0)千元时,在销售A,B商品中所获收益分
别为f(x)千元与g(x)千元,其中f(x)=2×,g(x)=4I(2x+1),如果该个体户准备共投入5千元销售
A,B两种商品,为使总收益最大,则B商品需投()千元
A
c.
D.
6.已知函数满足f(x)=f(2)e-f(o)x+2,则)的单讽递塔区间为()
4.(-,0)
B.(1,十o)
C.(-x,1)
D.(0,+)
7.若咽数f广inx+)xx在
3
上怡有2个极俏点,则实数a的取俏范围是()
2
B.
2引
c.〔89)
8.在数列{u}巾,Sn为共前n项,首项4,=1,又函数f(x)-x-.1si血x+(2n+)x+1,若f"(0)=0,
则S24()
4.22023-2024B.22-2025.202-2026D.22026-2027
二、多项选择题:本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有多项符合题目
的要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.定义:设f”(x)是(x)的导的数,”()是函数'(x)的导数,若方程"(x)=0有实数解x,则称点
(xf(》为函数y=()的拐点”.经过深究发见:任一个三次函数都有拐点”且拐点”就是三次函数
中心.已知函数()=以+x+〔b≠0)的对称巾心为,1),则下列说法巾正伯的
B.函数八)既有极大值叉有极小值
C.函数f(x)有个零点
D.过(-1,宁可以作三条占线与y=f图象相切
10.已函数f)=-1弓,则下列若论止确韵是()
A.f(x)的单调递增区间是0,,(山,+)
3.f(x)的值域为R
C.f(log22024)+.f(10g22023)=1
D若o)g-6,e(Q).ca+o小,则e=l
11.已知数列}满足4=1,+1=-,n∈N,则()
4.{a}足递诚数列
B.a.>h(n>2)
C.a024≤202x
1
1
…女
4.114.114,/1s
D.
同课章节目录
