第二单元 圆柱和圆锥(同步练习)-2023-2024学年苏教版数学六年级下册(无答案)
文档属性
| 名称 | 第二单元 圆柱和圆锥(同步练习)-2023-2024学年苏教版数学六年级下册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 513.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 17:53:30 | ||
图片预览


文档简介
圆柱和圆锥
熟练掌握圆柱和圆锥的各类公式;
对于生活中的实际问题做到心中有数;
3、能联系表面积和之间的共通处。
一.【认识圆柱和圆锥】
知识归纳:
一、圆柱:
1.圆柱是由两个完全相同的圆面和一个曲面三部分组成的。圆柱的上、下两个面叫作圆柱的底面,围成圆柱的曲面叫作圆
柱的侧面,圆柱两个底面之间的距离叫作圆柱的高。
2.圆柱的特征:圆柱的底面是两个完全相同的圆。圆柱的
侧面是曲面。一个圆柱有无数条高,且毎条高都相等。
二、圆锥:
1.圆锥是由一个底面和一个侧面两部分组成的。
2.圆锥的顶点到底面圆心的距离是圆锥的高。
3.圆锥的底面是一个圆,侧面是曲面,圆锥只有一条高。
相同点 不同点
底面形状 侧面 底面个数 侧面展开图 高
圆柱 圆 曲面 2 长方形或正方形(沿高) 无数条
圆锥 圆 曲面 1 扇形 1条
二.【试一试】
1、判断:半圆不可能是一个圆锥的侧面展开图。 ( )
2、一个圆柱形蛋糕盒的底面直径是20厘米,高是15厘米,用彩绳将它捆扎(如右图),打结处在圆心,打结部分长30厘米。求所用彩绳的全长是多少厘米。
三.【圆柱的表面积】
1、一根圆柱形木头长4米,底面半径是15厘米,把它截成4段后(截面平行于底面),表面积增加了多少平方厘米?
2、一顶圆柱形厨师帽,高是28厘米,帽顶直径20厘米,做5顶这样的帽子需要多少面料?(得数保留整十平方厘米)
3、如图,将高都为1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组合成一个物体。求这个物体的表面积。
四.【试一试】
1、一种圆柱形的罐头盒,底面直径是15厘米,高是20厘米。它的侧面贴有一张商标纸,商标纸的面积大约有多少平方厘米?
2、某地为节能环保,特推出“家家建沼气池”工程。正旭家挖出一个底面直径为3米,高是2.5米的圆柱沼气池,并在它的四周和池底抹上一层水泥。求抹水泥的面积。
3、小明所在学校的大厅里有8根一样的圆柱木柱,每根高5米,底面周长是1.2米。如果每平方米要用油漆0.8千克,请问刷这些木柱需要多少千克油漆?
4、一个圆柱罐头盒,高是12.56厘米,它的侧面展开图是一个正方形。做5个这样的罐头盒,至少需要多少铁皮?(得数保留整数)
五.【圆柱、圆锥的体积】
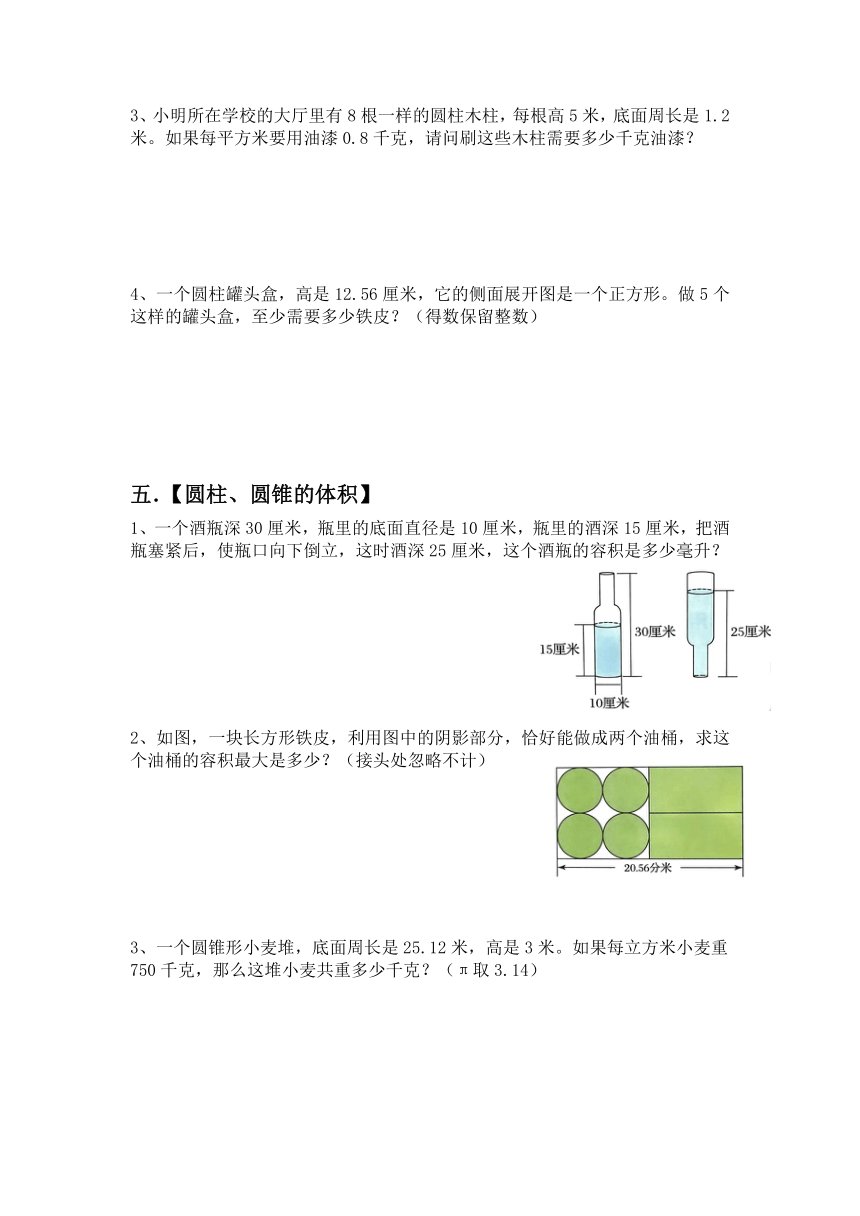
1、一个酒瓶深30厘米,瓶里的底面直径是10厘米,瓶里的酒深15厘米,把酒瓶塞紧后,使瓶口向下倒立,这时酒深25厘米,这个酒瓶的容积是多少毫升?
2、如图,一块长方形铁皮,利用图中的阴影部分,恰好能做成两个油桶,求这个油桶的容积最大是多少?(接头处忽略不计)
3、一个圆锥形小麦堆,底面周长是25.12米,高是3米。如果每立方米小麦重750千克,那么这堆小麦共重多少千克?(π取3.14)
4、把一个底面直径为6厘米、高为3厘米的圆柱形铅块熔铸成一个圆锥形铅锤。如果这个铅锤的底面积是42.39平方厘米,那么这个铅锤的高是多少厘米?
六.【试一试】
1、一种自来水管内直径是2厘米,水管内水的流速为每秒8厘米。照这样计算,1分钟流出的水是多少升?
2、一个圆柱形玻璃缸,底面半径是1分米,把一个钢球放人水中(钢球完全浸没水中且水未溢出),水面上升了0.1分米,钢球的体积是多少立方分米?(得数保留一位小数)
3、有一个长为8厘米,宽为6厘米的长方形纸片。现将纸片绕着一条边旋转一周,得到的圆柱的体积是多少立方厘米?
4、一个修路队把一堆底面半径为3米,高为1.5米的圆锥砂石铺在10米宽的公路上,若铺2厘米厚,则能铺多少米?
5、将一个底面直径是20厘米,高是18厘米的圆锥全部浸没在直径是40厘米的圆柱水槽中,水槽水面会升高多少厘米?
七.【课后练习】
1、(山东·期中)一种圆柱形蓄水池,从里面量深是2米,底面周长是31.4米,在它的内壁与底面抹上水泥。
(1)抹水泥部分的面积是多少?
(2)蓄水池能蓄水多少吨?(每立方米水重1.1吨)
2、(重庆·期末)一堆煤堆成圆锥形,底面半径是1.5米,高是1.1米,如果毎立方米的煤重约1.4吨,这堆煤约有多重?
3、(重庆·期末)一个底面半径为20厘米的圆柱形水箱中装有半箱水,现把一块石头浸没在水中,水面上升了5厘米(水未溢出),这块石头的体积是多少立方厘米?
4、如图所示,一个圆柱高8厘米,如果它的高增加2厘米,那么它的表面积将增加25.12平方厘米,求原来的圆柱的体积。
5、一个圆柱形水桶,桶内底面直径是4分米,桶内有半桶水,当把一些石子投人水中时(石子全部没人水中),水面上升了1.5分米(水未溢出),则这些石子的体积是多少立方分米?
八.【思维冲浪】
1、(甘肃·小升初)下图是底面半径为5厘米的圆柱从中间斜着截去一段后所得,那么它的体积是多少立方厘米?
2、(江苏·小升初)下图是一个圆柱形“牛肉罐头”的表面展开图,请你算一算,这个圆柱形“牛肉罐头”的容积是多少?(铁皮厚度忽略不计)
3、(江苏·小升初)如图,直角三角形三条边的长分别是3厘米、4厘米和5厘米,求绕斜边所在的直线旋转一周所形成的物体的体积。
熟练掌握圆柱和圆锥的各类公式;
对于生活中的实际问题做到心中有数;
3、能联系表面积和之间的共通处。
一.【认识圆柱和圆锥】
知识归纳:
一、圆柱:
1.圆柱是由两个完全相同的圆面和一个曲面三部分组成的。圆柱的上、下两个面叫作圆柱的底面,围成圆柱的曲面叫作圆
柱的侧面,圆柱两个底面之间的距离叫作圆柱的高。
2.圆柱的特征:圆柱的底面是两个完全相同的圆。圆柱的
侧面是曲面。一个圆柱有无数条高,且毎条高都相等。
二、圆锥:
1.圆锥是由一个底面和一个侧面两部分组成的。
2.圆锥的顶点到底面圆心的距离是圆锥的高。
3.圆锥的底面是一个圆,侧面是曲面,圆锥只有一条高。
相同点 不同点
底面形状 侧面 底面个数 侧面展开图 高
圆柱 圆 曲面 2 长方形或正方形(沿高) 无数条
圆锥 圆 曲面 1 扇形 1条
二.【试一试】
1、判断:半圆不可能是一个圆锥的侧面展开图。 ( )
2、一个圆柱形蛋糕盒的底面直径是20厘米,高是15厘米,用彩绳将它捆扎(如右图),打结处在圆心,打结部分长30厘米。求所用彩绳的全长是多少厘米。
三.【圆柱的表面积】
1、一根圆柱形木头长4米,底面半径是15厘米,把它截成4段后(截面平行于底面),表面积增加了多少平方厘米?
2、一顶圆柱形厨师帽,高是28厘米,帽顶直径20厘米,做5顶这样的帽子需要多少面料?(得数保留整十平方厘米)
3、如图,将高都为1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组合成一个物体。求这个物体的表面积。
四.【试一试】
1、一种圆柱形的罐头盒,底面直径是15厘米,高是20厘米。它的侧面贴有一张商标纸,商标纸的面积大约有多少平方厘米?
2、某地为节能环保,特推出“家家建沼气池”工程。正旭家挖出一个底面直径为3米,高是2.5米的圆柱沼气池,并在它的四周和池底抹上一层水泥。求抹水泥的面积。
3、小明所在学校的大厅里有8根一样的圆柱木柱,每根高5米,底面周长是1.2米。如果每平方米要用油漆0.8千克,请问刷这些木柱需要多少千克油漆?
4、一个圆柱罐头盒,高是12.56厘米,它的侧面展开图是一个正方形。做5个这样的罐头盒,至少需要多少铁皮?(得数保留整数)
五.【圆柱、圆锥的体积】
1、一个酒瓶深30厘米,瓶里的底面直径是10厘米,瓶里的酒深15厘米,把酒瓶塞紧后,使瓶口向下倒立,这时酒深25厘米,这个酒瓶的容积是多少毫升?
2、如图,一块长方形铁皮,利用图中的阴影部分,恰好能做成两个油桶,求这个油桶的容积最大是多少?(接头处忽略不计)
3、一个圆锥形小麦堆,底面周长是25.12米,高是3米。如果每立方米小麦重750千克,那么这堆小麦共重多少千克?(π取3.14)
4、把一个底面直径为6厘米、高为3厘米的圆柱形铅块熔铸成一个圆锥形铅锤。如果这个铅锤的底面积是42.39平方厘米,那么这个铅锤的高是多少厘米?
六.【试一试】
1、一种自来水管内直径是2厘米,水管内水的流速为每秒8厘米。照这样计算,1分钟流出的水是多少升?
2、一个圆柱形玻璃缸,底面半径是1分米,把一个钢球放人水中(钢球完全浸没水中且水未溢出),水面上升了0.1分米,钢球的体积是多少立方分米?(得数保留一位小数)
3、有一个长为8厘米,宽为6厘米的长方形纸片。现将纸片绕着一条边旋转一周,得到的圆柱的体积是多少立方厘米?
4、一个修路队把一堆底面半径为3米,高为1.5米的圆锥砂石铺在10米宽的公路上,若铺2厘米厚,则能铺多少米?
5、将一个底面直径是20厘米,高是18厘米的圆锥全部浸没在直径是40厘米的圆柱水槽中,水槽水面会升高多少厘米?
七.【课后练习】
1、(山东·期中)一种圆柱形蓄水池,从里面量深是2米,底面周长是31.4米,在它的内壁与底面抹上水泥。
(1)抹水泥部分的面积是多少?
(2)蓄水池能蓄水多少吨?(每立方米水重1.1吨)
2、(重庆·期末)一堆煤堆成圆锥形,底面半径是1.5米,高是1.1米,如果毎立方米的煤重约1.4吨,这堆煤约有多重?
3、(重庆·期末)一个底面半径为20厘米的圆柱形水箱中装有半箱水,现把一块石头浸没在水中,水面上升了5厘米(水未溢出),这块石头的体积是多少立方厘米?
4、如图所示,一个圆柱高8厘米,如果它的高增加2厘米,那么它的表面积将增加25.12平方厘米,求原来的圆柱的体积。
5、一个圆柱形水桶,桶内底面直径是4分米,桶内有半桶水,当把一些石子投人水中时(石子全部没人水中),水面上升了1.5分米(水未溢出),则这些石子的体积是多少立方分米?
八.【思维冲浪】
1、(甘肃·小升初)下图是底面半径为5厘米的圆柱从中间斜着截去一段后所得,那么它的体积是多少立方厘米?
2、(江苏·小升初)下图是一个圆柱形“牛肉罐头”的表面展开图,请你算一算,这个圆柱形“牛肉罐头”的容积是多少?(铁皮厚度忽略不计)
3、(江苏·小升初)如图,直角三角形三条边的长分别是3厘米、4厘米和5厘米,求绕斜边所在的直线旋转一周所形成的物体的体积。
