2024年浙江省宁波市中考数学精准模拟试卷(三)(含解析)
文档属性
| 名称 | 2024年浙江省宁波市中考数学精准模拟试卷(三)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 18:58:20 | ||
图片预览



文档简介
2024年浙江省宁波市中考数学精准模拟试卷(三)
一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)下列四个数中,最大的数是
A.1 B. C.0 D.
2.(3分)如图是由4个相同的小立方体搭成的几何体,这个几何体的主视图是
A. B. C. D.
3.(3分)下列运算正确的是
A. B. C. D.
4.(3分)甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是,,,.则射击成绩最稳定的是
A.甲 B.乙 C.丙 D.丁
5.(3分)燃放某种礼花弹时,为了确保安全,人在点燃导火线后要在燃放前转移到超过以外的安全区域.已知导火线的燃烧速度为,人离开的速度为,则导火线的长应满足的不等式为
A. B. C. D.
6.(3分)已知点,,,在反比例函数为常数)的图象上,且,下列结论一定正确的是
A. B. C. D.
7.(3分)如图,平行于主光轴的光线和经过凹透镜的折射后,折射光线,的反向延长线交于主光轴上一点.若,,则的度数是
A. B. C. D.
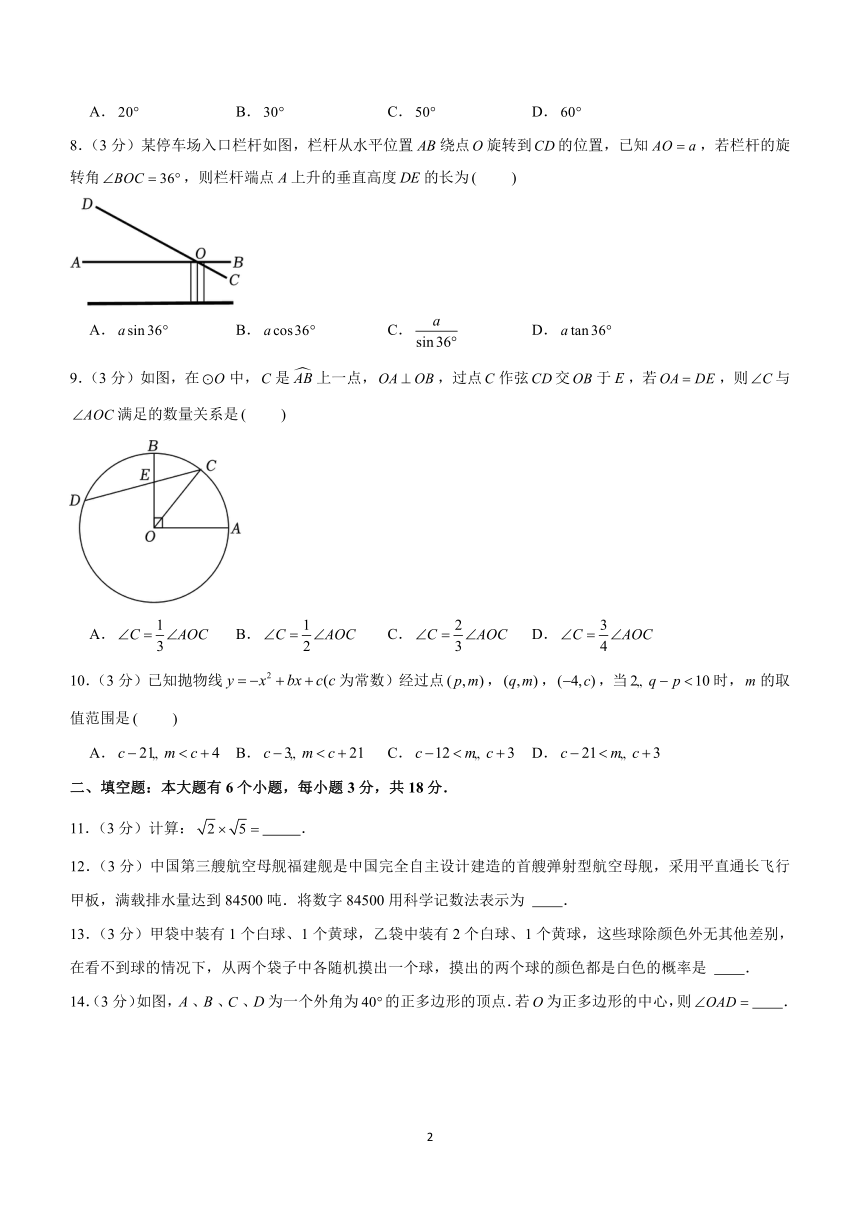
8.(3分)某停车场入口栏杆如图,栏杆从水平位置绕点旋转到的位置,已知,若栏杆的旋转角,则栏杆端点上升的垂直高度的长为
A. B. C. D.
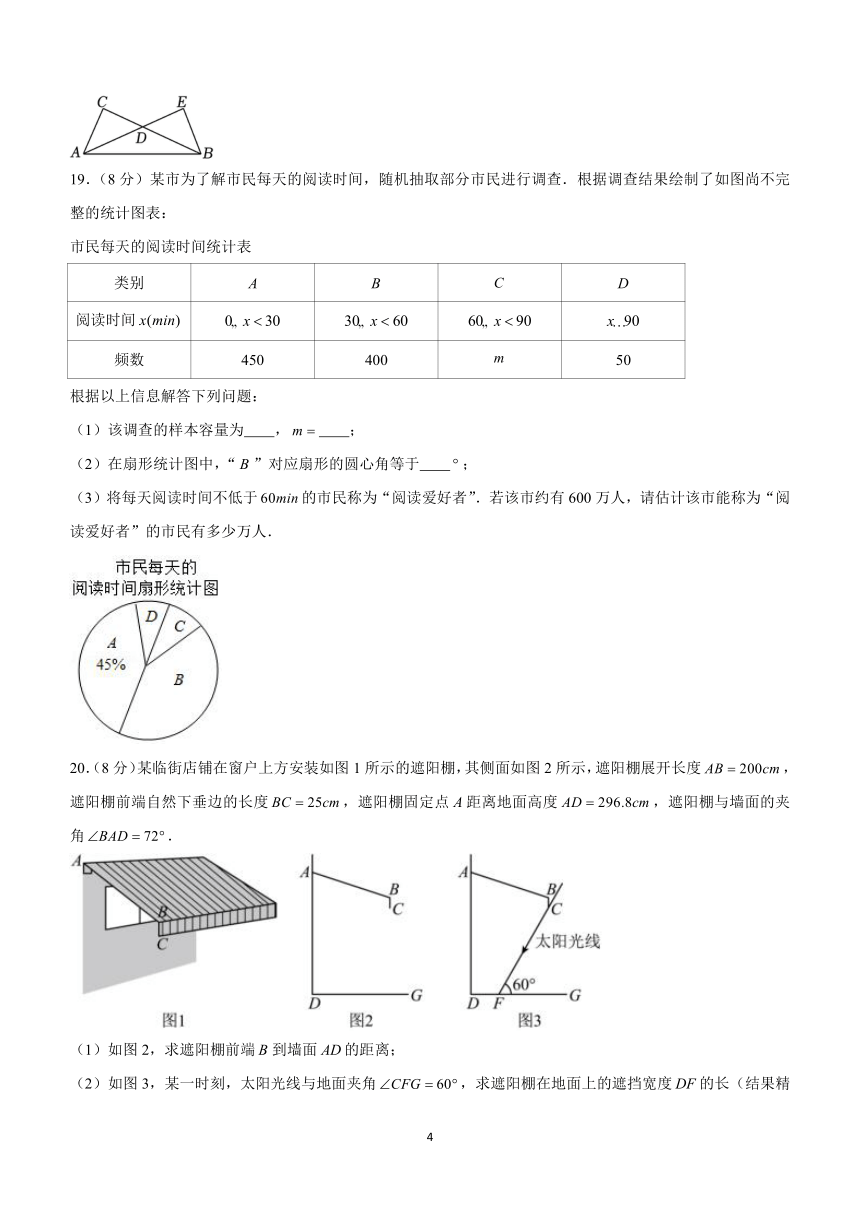
9.(3分)如图,在中,是上一点,,过点作弦交于,若,则与满足的数量关系是
A. B. C. D.
10.(3分)已知抛物线为常数)经过点,,,当时,的取值范围是
A. B. C. D.
二、填空题:本大题有6个小题,每小题3分,共18分.
11.(3分)计算: .
12.(3分)中国第三艘航空母舰福建舰是中国完全自主设计建造的首艘弹射型航空母舰,采用平直通长飞行甲板,满载排水量达到84500吨.将数字84500用科学记数法表示为 .
13.(3分)甲袋中装有1个白球、1个黄球,乙袋中装有2个白球、1个黄球,这些球除颜色外无其他差别,在看不到球的情况下,从两个袋子中各随机摸出一个球,摸出的两个球的颜色都是白色的概率是 .
14.(3分)如图,、、、为一个外角为的正多边形的顶点.若为正多边形的中心,则 .
15.(3分)幻方是一种中国传统游戏,我国古代的《洛书》中记载了最早的幻方九宫格.将9个数填入幻方的空格中,要求每一行、每一列以及两条对角线上的3个数之和相等,图1是一个已完成的幻方.图2是一个未完成的幻方,其中的值为 .
16.(3分)如图,在赵爽弦图中,正方形是由四个全等的直角三角形,,,和一个小正方形组成的.若把四个直角三角形分别沿斜边向外翻折,可得正方形,连接并延长,交于点.若正方形的面积为196,正方形的面积为4,则:
(1)正方形的面积为 .
(2)的长为 .
三、解答题:本大题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤.
17.(6分)已知代数式,,.从,,中任选两个分别作为分子、分母,组成一个分式,并化简该分式.
18.(6分)如图,在中,,的延长线于点,的延长线于点.
(1)求证:.
(2)若,,求的长.
19.(8分)某市为了解市民每天的阅读时间,随机抽取部分市民进行调查.根据调查结果绘制了如图尚不完整的统计图表:
市民每天的阅读时间统计表
类别
阅读时间
频数 450 400 50
根据以上信息解答下列问题:
(1)该调查的样本容量为 , ;
(2)在扇形统计图中,“”对应扇形的圆心角等于 ;
(3)将每天阅读时间不低于的市民称为“阅读爱好者”.若该市约有600万人,请估计该市能称为“阅读爱好者”的市民有多少万人.
20.(8分)某临街店铺在窗户上方安装如图1所示的遮阳棚,其侧面如图2所示,遮阳棚展开长度,遮阳棚前端自然下垂边的长度,遮阳棚固定点距离地面高度,遮阳棚与墙面的夹角.
(1)如图2,求遮阳棚前端到墙面的距离;
(2)如图3,某一时刻,太阳光线与地面夹角,求遮阳棚在地面上的遮挡宽度的长(结果精确到.(参考数据:,,,
21.(10分)我们规定:对于任意实数,,,有,▲,,其中等式右边是通常的乘法和减法运算,如:,▲,.
(1)已知,▲,,求的值.
(2)已知关于的方程,▲,有两个不相等的实数根,求的取值范围.
22.(10分)如图,以为直径的经过的顶点,和分别平分和,的延长线交于点,连接.
(1)求证:.
(2)若,,求的长.
23.(12分)北京环球影城主题乐园是世界第五个环球影城,乐园中既有功夫熊猫、小黄人乐园等小朋友喜欢的景区,又有过山车等深受年轻游客喜爱的游乐设施.过山车虽然惊险,但是安全保障措施非常到位.如图所示,F→E→G为过山车的一部分轨道,它可以看成一段抛物线.其中OE=15米,OF=22.5米.(轨道厚度忽略不计)
(1)求点F,E,G所在抛物线的函数解析式.
(2)在轨道距离地面10米处有两个位置P和G,当过山车运动到G处时,平行于地面向前运行了5米至K处,又进入下坡段K→H(K接口处轨道忽略不计).已知点K,H,Q所在抛物线的形状与点P,E,G所在抛物线的形状完全相同.在过山车从位置G到Q的过程中,当过山车距地面6.4米时,它离出发点的水平距离的最大值是多少?
(3)现需要在轨道下坡段F→E进行一种安全加固,建造某种材料的竖直和水平支架AM,CM,BN,DN,要求OA=AB.已知这种材料的价格是8000元/米,如何设计支架,会使造价最低?最低造价为多少元?
24.(12分)综合与实践.
【问题发现】
(1)如图1,在正方形中,为对角线上的动点,过点作的垂线,过点作的垂线,两条垂线交于点,连接,求证:.
【类比探究】
(2)如图2,在矩形中,为对角线上的动点,过点作的垂线,过点作的垂线,两条垂线交于点,且,连接,求的值.
【拓展延伸】
(3)如图3,在(2)的条件下,将改为直线上的动点,其余条件不变,取线段的中点,连接,.若,则当是直角三角形时,请求出的长.
2024年浙江省宁波市中考数学精准模拟试卷(三)
参考答案与试题解析
一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)下列四个数中,最大的数是
A.1 B. C.0 D.
【解答】解:四个答案中只有,为正数,
应从,中选;
,,
.
故选:.
2.(3分)如图是由4个相同的小立方体搭成的几何体,这个几何体的主视图是
A. B. C. D.
【解答】解:从正面看,底层有2个正方形,上层左边有1个正方形,
故选:.
3.(3分)下列运算正确的是
A. B. C. D.
【解答】解:.与4不是同类项,所以不能合并,原式错误,不符合题意;
.,计算正确,符合题意;
.,原式错误,不符合题意;
.,原式错误,不符合题意;
故选:.
4.(3分)甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是,,,.则射击成绩最稳定的是
A.甲 B.乙 C.丙 D.丁
【解答】解:,,,,
,
射击成绩最稳定的是甲,
故选:.
5.(3分)燃放某种礼花弹时,为了确保安全,人在点燃导火线后要在燃放前转移到超过以外的安全区域.已知导火线的燃烧速度为,人离开的速度为,则导火线的长应满足的不等式为
A. B. C. D.
【解答】解:人在点燃导火线后要在燃放前转移到超过以外的安全区域,
,
故选:.
6.(3分)已知点,,,在反比例函数为常数)的图象上,且,下列结论一定正确的是
A. B. C. D.
【解答】解:,
反比例函数为常数)的图象在第一、三象限,
点,,,在反比例函数为常数)的图象上,且,
,
,
故选:.
7.(3分)如图,平行于主光轴的光线和经过凹透镜的折射后,折射光线,的反向延长线交于主光轴上一点.若,,则的度数是
A. B. C. D.
【解答】解:,,
,,
,
,,
.
故选:.
8.(3分)某停车场入口栏杆如图,栏杆从水平位置绕点旋转到的位置,已知,若栏杆的旋转角,则栏杆端点上升的垂直高度的长为
A. B. C. D.
【解答】解:如图:过点作,垂足为,
由题意得:,,
在中,,
栏杆端点上升的垂直高度的长为,
故选:.
9.(3分)如图,在中,是上一点,,过点作弦交于,若,则与满足的数量关系是
A. B. C. D.
【解答】解:连接,
,
,
,
,
,
,,
,
,
是的一个外角,
,
,
,
,
故选:.
10.(3分)已知抛物线为常数)经过点,,,当时,的取值范围是
A. B. C. D.
【解答】解:点在抛物线图象上,
,
,
令,则有即,此时方程两根为、,,
,,
,
,
,
解得,
故选:.
二、填空题:本大题有6个小题,每小题3分,共18分.
11.(3分)计算: .
【解答】解:原式.
故答案为:.
12.(3分)中国第三艘航空母舰福建舰是中国完全自主设计建造的首艘弹射型航空母舰,采用平直通长飞行甲板,满载排水量达到84500吨.将数字84500用科学记数法表示为 .
【解答】解:.
故答案为:.
13.(3分)甲袋中装有1个白球、1个黄球,乙袋中装有2个白球、1个黄球,这些球除颜色外无其他差别,在看不到球的情况下,从两个袋子中各随机摸出一个球,摸出的两个球的颜色都是白色的概率是 .
【解答】解:列表如下:
白球 白球 黄球
白球 白球白球 白球白球 黄球白球
黄球 黄球白球 黄球白球 黄球黄球
共有6种等可能的结果,其中两个球的颜色都是白色的结果数为2种,
所以摸出的两个球的颜色都是白色的概率.
故答案为:.
14.(3分)如图,、、、为一个外角为的正多边形的顶点.若为正多边形的中心,则 .
【解答】解:连接、,
多边形的每个外角相等,且其和为,
据此可得多边形的边数为:,
,
.
.
故答案为:
15.(3分)幻方是一种中国传统游戏,我国古代的《洛书》中记载了最早的幻方九宫格.将9个数填入幻方的空格中,要求每一行、每一列以及两条对角线上的3个数之和相等,图1是一个已完成的幻方.图2是一个未完成的幻方,其中的值为 .
【解答】解:设左下角的空格中的数字为,
根据题意得:,
解得:,
.
故答案为:.
16.(3分)如图,在赵爽弦图中,正方形是由四个全等的直角三角形,,,和一个小正方形组成的.若把四个直角三角形分别沿斜边向外翻折,可得正方形,连接并延长,交于点.若正方形的面积为196,正方形的面积为4,则:
(1)正方形的面积为 100 .
(2)的长为 .
【解答】解:(1)设每个小直角三角形的长直角边长为,短直角边长为,斜边长为.
正方形的面积为196,正方形的面积为4,
.
,,
.
解得:.
.
正方形的面积为:.
故答案为100;
(2)设交于点.
由题意得:,,
.
.
.
四边形是正方形,
.
.
由题意得:,.
.
同理.
.
由题意得:,,.
.
.
故答案为:7.9.
三、解答题:本大题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤.
17.(6分)已知代数式,,.从,,中任选两个分别作为分子、分母,组成一个分式,并化简该分式.
【解答】解:选择作为分子,作为分母,
.
18.(6分)如图,在中,,的延长线于点,的延长线于点.
(1)求证:.
(2)若,,求的长.
【解答】(1)证明:,
,
又,,
,
在和,
,
;
(2)解:由(1)知:,
,
,
.
19.(8分)某市为了解市民每天的阅读时间,随机抽取部分市民进行调查.根据调查结果绘制了如图尚不完整的统计图表:
市民每天的阅读时间统计表
类别
阅读时间
频数 450 400 50
根据以上信息解答下列问题:
(1)该调查的样本容量为 1000 , ;
(2)在扇形统计图中,“”对应扇形的圆心角等于 ;
(3)将每天阅读时间不低于的市民称为“阅读爱好者”.若该市约有600万人,请估计该市能称为“阅读爱好者”的市民有多少万人.
【解答】解:(1),
.
故答案为:1000,100;
(2).
即在扇形统计图中,“”对应扇形的圆心角等于.
故答案为:144;
(3)(万人).
答:估计该市能称为“阅读爱好者”的市民有90万人.
20.(8分)某临街店铺在窗户上方安装如图1所示的遮阳棚,其侧面如图2所示,遮阳棚展开长度,遮阳棚前端自然下垂边的长度,遮阳棚固定点距离地面高度,遮阳棚与墙面的夹角.
(1)如图2,求遮阳棚前端到墙面的距离;
(2)如图3,某一时刻,太阳光线与地面夹角,求遮阳棚在地面上的遮挡宽度的长(结果精确到.(参考数据:,,,
【解答】解:(1)如图,作于,
,.
在中,,即,
,
答:遮阳棚前端到墙面的距离约为;
(2)解:如图3,作于,于,延长交于,则,
四边形,四边形是矩形,
由(1)得,
,
在中,,即,
,
由题意得:,
,
,
在中,,即,
,
,
答:遮阳棚在地面上的遮挡宽度的长约为.
21.(10分)我们规定:对于任意实数,,,有,▲,,其中等式右边是通常的乘法和减法运算,如:,▲,.
(1)已知,▲,,求的值.
(2)已知关于的方程,▲,有两个不相等的实数根,求的取值范围.
【解答】解:(1)根据题意得得,
解得,
即的值为3;
(2)根据题意得,
整理得,
关于的方程,▲,有两个不相等的实数根,
△且,
解得且.
22.(10分)如图,以为直径的经过的顶点,和分别平分和,的延长线交于点,连接.
(1)求证:.
(2)若,,求的长.
【解答】(1)证明:和分别平分和,
,,
和是所对的圆周角,
,
,
,
是的外角,
,
,
;
(2)解:连接交于点,
平分,
,
,
,
即,,
,
是的中位线,
,
,
,
,
为直径,
,
由勾股定理得,,
,
在中,由勾股定理得,,
由(1)知,
为直径,
,
由勾股定理得,.
23.(12分)北京环球影城主题乐园是世界第五个环球影城,乐园中既有功夫熊猫、小黄人乐园等小朋友喜欢的景区,又有过山车等深受年轻游客喜爱的游乐设施.过山车虽然惊险,但是安全保障措施非常到位.如图所示,F→E→G为过山车的一部分轨道,它可以看成一段抛物线.其中OE=15米,OF=22.5米.(轨道厚度忽略不计)
(1)求点F,E,G所在抛物线的函数解析式.
(2)在轨道距离地面10米处有两个位置P和G,当过山车运动到G处时,平行于地面向前运行了5米至K处,又进入下坡段K→H(K接口处轨道忽略不计).已知点K,H,Q所在抛物线的形状与点P,E,G所在抛物线的形状完全相同.在过山车从位置G到Q的过程中,当过山车距地面6.4米时,它离出发点的水平距离的最大值是多少?
(3)现需要在轨道下坡段F→E进行一种安全加固,建造某种材料的竖直和水平支架AM,CM,BN,DN,要求OA=AB.已知这种材料的价格是8000元/米,如何设计支架,会使造价最低?最低造价为多少元?
【解答】解:(1)∵OE=15,
∴E(15,0),
∴点F,E,G所在抛物线的对称轴为直线x=15,
由图象可设抛物线解析式为y=a(x﹣15)2,
把F(0,22.5)代入得:a(0﹣15)2=22.5,解得a=,
∴点F,E,G所在抛物线的解析式为:y=(x﹣15)2;
(2)当y=10时,=10,解得x1=5,x2=25,
∴P(5,10),G(25,10),PG=25﹣5=20,
∵点K,H,Q所在抛物线的形状与点P,E,G所在抛物线的形状完全相同,
∴点K,H,Q所在抛物线由点P,E,G所在抛物线向右平移(PG+GK)个单位,
∵PG=20,GK=5,
∴PG+GK=25.
∴点K,H,Q所在抛物线为y2=(x﹣15﹣25)2=,
令y2=6.4,则(x﹣40)2=6.4,解得x1=32,x2=48(水平距离最大),
∴离出发点的水平距离的最大值是48米.
(3)设OA=AB=a,则A(a,0),B(2a,0),yM==,yN=(2a﹣15)2=(4a2﹣60a+225),
∴支架长度=AM+CM+BN+DN=+a+(4a2﹣60a+225)+2a==(a﹣6)2+27,
∵,抛物线开口向上,
∴当a=6时,支架长度最短,最短为27米,
此时,CM=6,DN=12,AM=8.1,BM=0.9,
∴8000×27=216000(元),
故当OA=AB=6米时,即CM=6,DN=12,AM=8.1,BM=0.9时,使造价最低,最低造价为216000元.
24.(12分)综合与实践.
【问题发现】
(1)如图1,在正方形中,为对角线上的动点,过点作的垂线,过点作的垂线,两条垂线交于点,连接,求证:.
【类比探究】
(2)如图2,在矩形中,为对角线上的动点,过点作的垂线,过点作的垂线,两条垂线交于点,且,连接,求的值.
【拓展延伸】
(3)如图3,在(2)的条件下,将改为直线上的动点,其余条件不变,取线段的中点,连接,.若,则当是直角三角形时,请求出的长.
【解答】(1)证明:四边形是正方形,
,,,
,,
,
,,
,
;
(2)解:,,
,
点,点,点,点四点共圆,
,
,
,,
,
,
,
;
(3)解:由(2)知:,
,
,
,
,
,
为的中点,
,
由(2)知,
,
,
又是直角三角形,
,
,
设,则,
,,
,
,
,
,
,
或(不合题意,舍去),
当或时,点不存在,
当在延长线上时,设,则,
,,
,
,
,
,
,
(不合题意,舍去)或,
综上所述,的长为或.
一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)下列四个数中,最大的数是
A.1 B. C.0 D.
2.(3分)如图是由4个相同的小立方体搭成的几何体,这个几何体的主视图是
A. B. C. D.
3.(3分)下列运算正确的是
A. B. C. D.
4.(3分)甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是,,,.则射击成绩最稳定的是
A.甲 B.乙 C.丙 D.丁
5.(3分)燃放某种礼花弹时,为了确保安全,人在点燃导火线后要在燃放前转移到超过以外的安全区域.已知导火线的燃烧速度为,人离开的速度为,则导火线的长应满足的不等式为
A. B. C. D.
6.(3分)已知点,,,在反比例函数为常数)的图象上,且,下列结论一定正确的是
A. B. C. D.
7.(3分)如图,平行于主光轴的光线和经过凹透镜的折射后,折射光线,的反向延长线交于主光轴上一点.若,,则的度数是
A. B. C. D.
8.(3分)某停车场入口栏杆如图,栏杆从水平位置绕点旋转到的位置,已知,若栏杆的旋转角,则栏杆端点上升的垂直高度的长为
A. B. C. D.
9.(3分)如图,在中,是上一点,,过点作弦交于,若,则与满足的数量关系是
A. B. C. D.
10.(3分)已知抛物线为常数)经过点,,,当时,的取值范围是
A. B. C. D.
二、填空题:本大题有6个小题,每小题3分,共18分.
11.(3分)计算: .
12.(3分)中国第三艘航空母舰福建舰是中国完全自主设计建造的首艘弹射型航空母舰,采用平直通长飞行甲板,满载排水量达到84500吨.将数字84500用科学记数法表示为 .
13.(3分)甲袋中装有1个白球、1个黄球,乙袋中装有2个白球、1个黄球,这些球除颜色外无其他差别,在看不到球的情况下,从两个袋子中各随机摸出一个球,摸出的两个球的颜色都是白色的概率是 .
14.(3分)如图,、、、为一个外角为的正多边形的顶点.若为正多边形的中心,则 .
15.(3分)幻方是一种中国传统游戏,我国古代的《洛书》中记载了最早的幻方九宫格.将9个数填入幻方的空格中,要求每一行、每一列以及两条对角线上的3个数之和相等,图1是一个已完成的幻方.图2是一个未完成的幻方,其中的值为 .
16.(3分)如图,在赵爽弦图中,正方形是由四个全等的直角三角形,,,和一个小正方形组成的.若把四个直角三角形分别沿斜边向外翻折,可得正方形,连接并延长,交于点.若正方形的面积为196,正方形的面积为4,则:
(1)正方形的面积为 .
(2)的长为 .
三、解答题:本大题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤.
17.(6分)已知代数式,,.从,,中任选两个分别作为分子、分母,组成一个分式,并化简该分式.
18.(6分)如图,在中,,的延长线于点,的延长线于点.
(1)求证:.
(2)若,,求的长.
19.(8分)某市为了解市民每天的阅读时间,随机抽取部分市民进行调查.根据调查结果绘制了如图尚不完整的统计图表:
市民每天的阅读时间统计表
类别
阅读时间
频数 450 400 50
根据以上信息解答下列问题:
(1)该调查的样本容量为 , ;
(2)在扇形统计图中,“”对应扇形的圆心角等于 ;
(3)将每天阅读时间不低于的市民称为“阅读爱好者”.若该市约有600万人,请估计该市能称为“阅读爱好者”的市民有多少万人.
20.(8分)某临街店铺在窗户上方安装如图1所示的遮阳棚,其侧面如图2所示,遮阳棚展开长度,遮阳棚前端自然下垂边的长度,遮阳棚固定点距离地面高度,遮阳棚与墙面的夹角.
(1)如图2,求遮阳棚前端到墙面的距离;
(2)如图3,某一时刻,太阳光线与地面夹角,求遮阳棚在地面上的遮挡宽度的长(结果精确到.(参考数据:,,,
21.(10分)我们规定:对于任意实数,,,有,▲,,其中等式右边是通常的乘法和减法运算,如:,▲,.
(1)已知,▲,,求的值.
(2)已知关于的方程,▲,有两个不相等的实数根,求的取值范围.
22.(10分)如图,以为直径的经过的顶点,和分别平分和,的延长线交于点,连接.
(1)求证:.
(2)若,,求的长.
23.(12分)北京环球影城主题乐园是世界第五个环球影城,乐园中既有功夫熊猫、小黄人乐园等小朋友喜欢的景区,又有过山车等深受年轻游客喜爱的游乐设施.过山车虽然惊险,但是安全保障措施非常到位.如图所示,F→E→G为过山车的一部分轨道,它可以看成一段抛物线.其中OE=15米,OF=22.5米.(轨道厚度忽略不计)
(1)求点F,E,G所在抛物线的函数解析式.
(2)在轨道距离地面10米处有两个位置P和G,当过山车运动到G处时,平行于地面向前运行了5米至K处,又进入下坡段K→H(K接口处轨道忽略不计).已知点K,H,Q所在抛物线的形状与点P,E,G所在抛物线的形状完全相同.在过山车从位置G到Q的过程中,当过山车距地面6.4米时,它离出发点的水平距离的最大值是多少?
(3)现需要在轨道下坡段F→E进行一种安全加固,建造某种材料的竖直和水平支架AM,CM,BN,DN,要求OA=AB.已知这种材料的价格是8000元/米,如何设计支架,会使造价最低?最低造价为多少元?
24.(12分)综合与实践.
【问题发现】
(1)如图1,在正方形中,为对角线上的动点,过点作的垂线,过点作的垂线,两条垂线交于点,连接,求证:.
【类比探究】
(2)如图2,在矩形中,为对角线上的动点,过点作的垂线,过点作的垂线,两条垂线交于点,且,连接,求的值.
【拓展延伸】
(3)如图3,在(2)的条件下,将改为直线上的动点,其余条件不变,取线段的中点,连接,.若,则当是直角三角形时,请求出的长.
2024年浙江省宁波市中考数学精准模拟试卷(三)
参考答案与试题解析
一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)下列四个数中,最大的数是
A.1 B. C.0 D.
【解答】解:四个答案中只有,为正数,
应从,中选;
,,
.
故选:.
2.(3分)如图是由4个相同的小立方体搭成的几何体,这个几何体的主视图是
A. B. C. D.
【解答】解:从正面看,底层有2个正方形,上层左边有1个正方形,
故选:.
3.(3分)下列运算正确的是
A. B. C. D.
【解答】解:.与4不是同类项,所以不能合并,原式错误,不符合题意;
.,计算正确,符合题意;
.,原式错误,不符合题意;
.,原式错误,不符合题意;
故选:.
4.(3分)甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是,,,.则射击成绩最稳定的是
A.甲 B.乙 C.丙 D.丁
【解答】解:,,,,
,
射击成绩最稳定的是甲,
故选:.
5.(3分)燃放某种礼花弹时,为了确保安全,人在点燃导火线后要在燃放前转移到超过以外的安全区域.已知导火线的燃烧速度为,人离开的速度为,则导火线的长应满足的不等式为
A. B. C. D.
【解答】解:人在点燃导火线后要在燃放前转移到超过以外的安全区域,
,
故选:.
6.(3分)已知点,,,在反比例函数为常数)的图象上,且,下列结论一定正确的是
A. B. C. D.
【解答】解:,
反比例函数为常数)的图象在第一、三象限,
点,,,在反比例函数为常数)的图象上,且,
,
,
故选:.
7.(3分)如图,平行于主光轴的光线和经过凹透镜的折射后,折射光线,的反向延长线交于主光轴上一点.若,,则的度数是
A. B. C. D.
【解答】解:,,
,,
,
,,
.
故选:.
8.(3分)某停车场入口栏杆如图,栏杆从水平位置绕点旋转到的位置,已知,若栏杆的旋转角,则栏杆端点上升的垂直高度的长为
A. B. C. D.
【解答】解:如图:过点作,垂足为,
由题意得:,,
在中,,
栏杆端点上升的垂直高度的长为,
故选:.
9.(3分)如图,在中,是上一点,,过点作弦交于,若,则与满足的数量关系是
A. B. C. D.
【解答】解:连接,
,
,
,
,
,
,,
,
,
是的一个外角,
,
,
,
,
故选:.
10.(3分)已知抛物线为常数)经过点,,,当时,的取值范围是
A. B. C. D.
【解答】解:点在抛物线图象上,
,
,
令,则有即,此时方程两根为、,,
,,
,
,
,
解得,
故选:.
二、填空题:本大题有6个小题,每小题3分,共18分.
11.(3分)计算: .
【解答】解:原式.
故答案为:.
12.(3分)中国第三艘航空母舰福建舰是中国完全自主设计建造的首艘弹射型航空母舰,采用平直通长飞行甲板,满载排水量达到84500吨.将数字84500用科学记数法表示为 .
【解答】解:.
故答案为:.
13.(3分)甲袋中装有1个白球、1个黄球,乙袋中装有2个白球、1个黄球,这些球除颜色外无其他差别,在看不到球的情况下,从两个袋子中各随机摸出一个球,摸出的两个球的颜色都是白色的概率是 .
【解答】解:列表如下:
白球 白球 黄球
白球 白球白球 白球白球 黄球白球
黄球 黄球白球 黄球白球 黄球黄球
共有6种等可能的结果,其中两个球的颜色都是白色的结果数为2种,
所以摸出的两个球的颜色都是白色的概率.
故答案为:.
14.(3分)如图,、、、为一个外角为的正多边形的顶点.若为正多边形的中心,则 .
【解答】解:连接、,
多边形的每个外角相等,且其和为,
据此可得多边形的边数为:,
,
.
.
故答案为:
15.(3分)幻方是一种中国传统游戏,我国古代的《洛书》中记载了最早的幻方九宫格.将9个数填入幻方的空格中,要求每一行、每一列以及两条对角线上的3个数之和相等,图1是一个已完成的幻方.图2是一个未完成的幻方,其中的值为 .
【解答】解:设左下角的空格中的数字为,
根据题意得:,
解得:,
.
故答案为:.
16.(3分)如图,在赵爽弦图中,正方形是由四个全等的直角三角形,,,和一个小正方形组成的.若把四个直角三角形分别沿斜边向外翻折,可得正方形,连接并延长,交于点.若正方形的面积为196,正方形的面积为4,则:
(1)正方形的面积为 100 .
(2)的长为 .
【解答】解:(1)设每个小直角三角形的长直角边长为,短直角边长为,斜边长为.
正方形的面积为196,正方形的面积为4,
.
,,
.
解得:.
.
正方形的面积为:.
故答案为100;
(2)设交于点.
由题意得:,,
.
.
.
四边形是正方形,
.
.
由题意得:,.
.
同理.
.
由题意得:,,.
.
.
故答案为:7.9.
三、解答题:本大题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤.
17.(6分)已知代数式,,.从,,中任选两个分别作为分子、分母,组成一个分式,并化简该分式.
【解答】解:选择作为分子,作为分母,
.
18.(6分)如图,在中,,的延长线于点,的延长线于点.
(1)求证:.
(2)若,,求的长.
【解答】(1)证明:,
,
又,,
,
在和,
,
;
(2)解:由(1)知:,
,
,
.
19.(8分)某市为了解市民每天的阅读时间,随机抽取部分市民进行调查.根据调查结果绘制了如图尚不完整的统计图表:
市民每天的阅读时间统计表
类别
阅读时间
频数 450 400 50
根据以上信息解答下列问题:
(1)该调查的样本容量为 1000 , ;
(2)在扇形统计图中,“”对应扇形的圆心角等于 ;
(3)将每天阅读时间不低于的市民称为“阅读爱好者”.若该市约有600万人,请估计该市能称为“阅读爱好者”的市民有多少万人.
【解答】解:(1),
.
故答案为:1000,100;
(2).
即在扇形统计图中,“”对应扇形的圆心角等于.
故答案为:144;
(3)(万人).
答:估计该市能称为“阅读爱好者”的市民有90万人.
20.(8分)某临街店铺在窗户上方安装如图1所示的遮阳棚,其侧面如图2所示,遮阳棚展开长度,遮阳棚前端自然下垂边的长度,遮阳棚固定点距离地面高度,遮阳棚与墙面的夹角.
(1)如图2,求遮阳棚前端到墙面的距离;
(2)如图3,某一时刻,太阳光线与地面夹角,求遮阳棚在地面上的遮挡宽度的长(结果精确到.(参考数据:,,,
【解答】解:(1)如图,作于,
,.
在中,,即,
,
答:遮阳棚前端到墙面的距离约为;
(2)解:如图3,作于,于,延长交于,则,
四边形,四边形是矩形,
由(1)得,
,
在中,,即,
,
由题意得:,
,
,
在中,,即,
,
,
答:遮阳棚在地面上的遮挡宽度的长约为.
21.(10分)我们规定:对于任意实数,,,有,▲,,其中等式右边是通常的乘法和减法运算,如:,▲,.
(1)已知,▲,,求的值.
(2)已知关于的方程,▲,有两个不相等的实数根,求的取值范围.
【解答】解:(1)根据题意得得,
解得,
即的值为3;
(2)根据题意得,
整理得,
关于的方程,▲,有两个不相等的实数根,
△且,
解得且.
22.(10分)如图,以为直径的经过的顶点,和分别平分和,的延长线交于点,连接.
(1)求证:.
(2)若,,求的长.
【解答】(1)证明:和分别平分和,
,,
和是所对的圆周角,
,
,
,
是的外角,
,
,
;
(2)解:连接交于点,
平分,
,
,
,
即,,
,
是的中位线,
,
,
,
,
为直径,
,
由勾股定理得,,
,
在中,由勾股定理得,,
由(1)知,
为直径,
,
由勾股定理得,.
23.(12分)北京环球影城主题乐园是世界第五个环球影城,乐园中既有功夫熊猫、小黄人乐园等小朋友喜欢的景区,又有过山车等深受年轻游客喜爱的游乐设施.过山车虽然惊险,但是安全保障措施非常到位.如图所示,F→E→G为过山车的一部分轨道,它可以看成一段抛物线.其中OE=15米,OF=22.5米.(轨道厚度忽略不计)
(1)求点F,E,G所在抛物线的函数解析式.
(2)在轨道距离地面10米处有两个位置P和G,当过山车运动到G处时,平行于地面向前运行了5米至K处,又进入下坡段K→H(K接口处轨道忽略不计).已知点K,H,Q所在抛物线的形状与点P,E,G所在抛物线的形状完全相同.在过山车从位置G到Q的过程中,当过山车距地面6.4米时,它离出发点的水平距离的最大值是多少?
(3)现需要在轨道下坡段F→E进行一种安全加固,建造某种材料的竖直和水平支架AM,CM,BN,DN,要求OA=AB.已知这种材料的价格是8000元/米,如何设计支架,会使造价最低?最低造价为多少元?
【解答】解:(1)∵OE=15,
∴E(15,0),
∴点F,E,G所在抛物线的对称轴为直线x=15,
由图象可设抛物线解析式为y=a(x﹣15)2,
把F(0,22.5)代入得:a(0﹣15)2=22.5,解得a=,
∴点F,E,G所在抛物线的解析式为:y=(x﹣15)2;
(2)当y=10时,=10,解得x1=5,x2=25,
∴P(5,10),G(25,10),PG=25﹣5=20,
∵点K,H,Q所在抛物线的形状与点P,E,G所在抛物线的形状完全相同,
∴点K,H,Q所在抛物线由点P,E,G所在抛物线向右平移(PG+GK)个单位,
∵PG=20,GK=5,
∴PG+GK=25.
∴点K,H,Q所在抛物线为y2=(x﹣15﹣25)2=,
令y2=6.4,则(x﹣40)2=6.4,解得x1=32,x2=48(水平距离最大),
∴离出发点的水平距离的最大值是48米.
(3)设OA=AB=a,则A(a,0),B(2a,0),yM==,yN=(2a﹣15)2=(4a2﹣60a+225),
∴支架长度=AM+CM+BN+DN=+a+(4a2﹣60a+225)+2a==(a﹣6)2+27,
∵,抛物线开口向上,
∴当a=6时,支架长度最短,最短为27米,
此时,CM=6,DN=12,AM=8.1,BM=0.9,
∴8000×27=216000(元),
故当OA=AB=6米时,即CM=6,DN=12,AM=8.1,BM=0.9时,使造价最低,最低造价为216000元.
24.(12分)综合与实践.
【问题发现】
(1)如图1,在正方形中,为对角线上的动点,过点作的垂线,过点作的垂线,两条垂线交于点,连接,求证:.
【类比探究】
(2)如图2,在矩形中,为对角线上的动点,过点作的垂线,过点作的垂线,两条垂线交于点,且,连接,求的值.
【拓展延伸】
(3)如图3,在(2)的条件下,将改为直线上的动点,其余条件不变,取线段的中点,连接,.若,则当是直角三角形时,请求出的长.
【解答】(1)证明:四边形是正方形,
,,,
,,
,
,,
,
;
(2)解:,,
,
点,点,点,点四点共圆,
,
,
,,
,
,
,
;
(3)解:由(2)知:,
,
,
,
,
,
为的中点,
,
由(2)知,
,
,
又是直角三角形,
,
,
设,则,
,,
,
,
,
,
,
或(不合题意,舍去),
当或时,点不存在,
当在延长线上时,设,则,
,,
,
,
,
,
,
(不合题意,舍去)或,
综上所述,的长为或.
同课章节目录
