第八章 8.3.1 棱柱、棱锥、棱台的表面积和体积(26页ppt)
文档属性
| 名称 | 第八章 8.3.1 棱柱、棱锥、棱台的表面积和体积(26页ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 08:43:47 | ||
图片预览






文档简介
(共26张PPT)
第七章
8.3 简单几何体的表面积和体积
人教A版(2019)
前面我们分别认识了基本立体图形的结构特征和平面表示,本节进一步认识简单几何体的表面积和体积. 表面积是几何体表面的面积,它表示几何体表面的大小,体积是几何体所占空间的大小.
第七章
8.3.1 棱柱、棱锥、棱台的表面积和体积
人教A版(2019)
教学目标
学习目标 数学素养
1.了解棱柱、棱锥、棱台的表面积和体积计算公式. 1.数学运算素养.
2.理解并掌握侧面展开图与几何体的表面积之间的关系,并能运用计算公式求几何体的表面积和体积. 2.数学抽象素养.
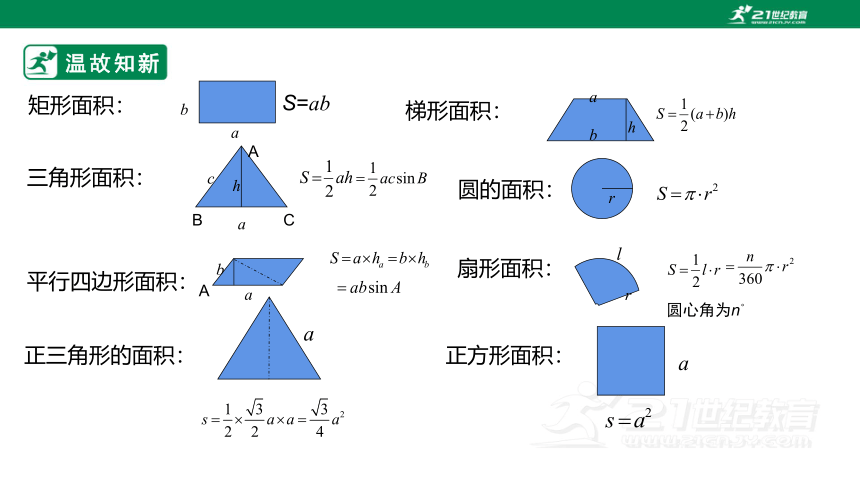
温故知新
矩形面积:
S=ab
a
b
三角形面积:
a
h
B
C
A
c
平行四边形面积:
a
b
A
梯形面积:
a
b
h
圆的面积:
r
扇形面积:
r
圆心角为n°
正三角形的面积:
a
正方形面积:
a
温故知新
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
长方体、正方体表面积
展开图
平面图形面积
空间问题
平面问题
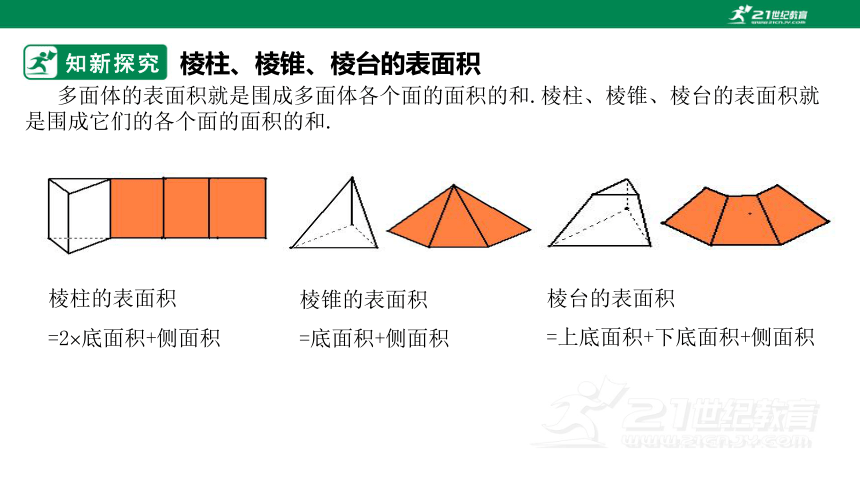
知新探究
多面体的表面积就是围成多面体各个面的面积的和.棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.
棱柱的表面积
=2 底面积+侧面积
棱锥的表面积
=底面积+侧面积
棱台的表面积
=上底面积+下底面积+侧面积
棱柱、棱锥、棱台的表面积
知新探究
【例1】如图,四面体P-ABC的各棱长均为a,求它的表面积.
分析:因为四面体的四个面是全等的等边三角形,所以四面体的表面积等于其中任何一个面的面积的4倍.
棱柱、棱锥、棱台的表面积
B
C
A
P
解:
∵△PBC是正三角形,其边长为a,
∴.
因此,四面体P-ABC的表面积
.
知新探究
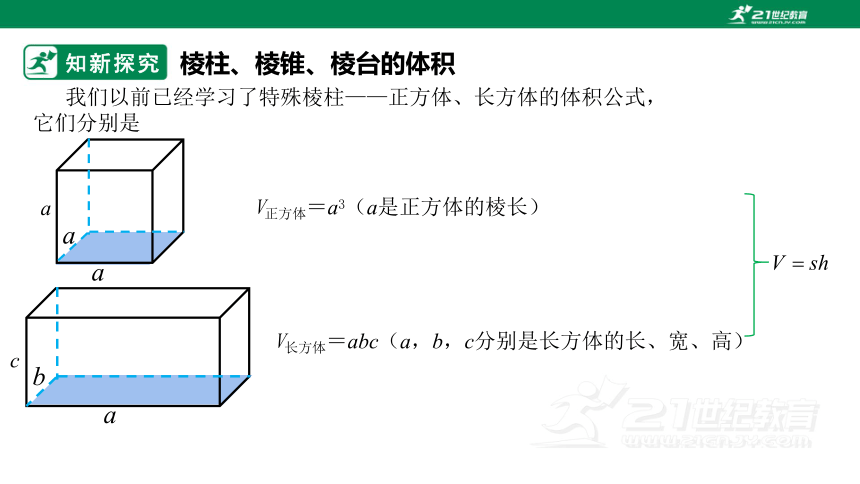
棱柱、棱锥、棱台的体积
我们以前已经学习了特殊棱柱——正方体、长方体的体积公式,
它们分别是
V正方体=a3(a是正方体的棱长)
V长方体=abc(a,b,c分别是长方体的长、宽、高)
a
c
知新探究
棱柱、棱锥、棱台的体积
一般地,如果棱柱的底面面积为S,高为h,那么这个棱柱的体积
V棱柱=Sh
棱柱的高
棱柱的高是指两底面之间的距离,即从一底面上任意一点向另一个底面作垂线,这点与垂足之间的距离.
知新探究
棱柱、棱锥、棱台的体积
关于体积有如下几个原理:
⑴相同的几何体的体积相等;
⑵一个几何体的体积等于它的各部分体积之和;
⑶等底面积等高的两个同类几何体的体积相等;
⑷体积相等的两个几何体叫做等积体.
知新探究
棱柱、棱锥、棱台的体积
将一个三棱柱按如图所示分解成三个三棱锥,那么这三个三棱锥的体积有什么关系?它们与三棱柱的体积有什么关系?
1
2
3
1
2
3
Sh
Sh
知新探究
棱柱、棱锥、棱台的体积
推广到一般的棱锥,你猜想锥体的体积公式是什么?
高h
底面积S
如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍.
因此,一般地,如果棱锥的底面面积为S,高为h,那么该棱锥的体积
.
棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.
知新探究
棱柱、棱锥、棱台的体积
由于棱台是由棱锥截成的,因此可以利用两个棱锥的体积差,得到棱台的体积公式
棱台的高
.
其中S′,S分别为棱台的上、下底面面积,h为棱台的高.
棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间的距离.
知新探究
棱柱、棱锥、棱台的体积
观察棱柱、棱锥、棱台的体积公式:
,,.
它们之间有什么关系 你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗
V棱柱=Sh
V棱锥= Sh
V棱台
上底扩大
S'=S
S'=S
S'=0
上底缩小
S'=0
知新探究
【例2】如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5cm,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米(精确到0.01立方米)?(计算漏斗的容积时不考虑漏斗的厚度)
分析:漏斗由两个多面体组成,其容积就是两个多面体的体积.
知新探究
【例2】如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5cm,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米(精确到0.01立方米)?(计算漏斗的容积时不考虑漏斗的厚度)
解:
由题意知
(m3).
(m3).
所以这个漏斗的容积
(m3)
初试身手
1.侧面都是等腰直角三角形的正三棱锥,底面边长为a,则该棱锥的表面积是( )
A. B. C. D.
解:
设正三棱锥的侧棱长为b,则由已知条件知,b2+b2=a2,,
∴,
故选A.
初试身手
2.已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,则该四棱台的表面积为 .
解:
如图,在四棱台ABCD-A1B1C1D1中,过B1作B1F BC,垂足为F,
在Rt△B1FB中,BF=,B1B=8,
∴B1F=.
∴.
∴四棱台的表面积S=
=.
初试身手
3.⑴如图,底面为矩形的四棱锥P-ABCD,PA为四棱锥的高,PA=AB=1,BC=2,则四棱锥P-ABCD的体积为 .
⑵已知有一正四棱台的上底边长为4cm,下底边长为8cm,高为3cm,
则其体积为 cm3.
解:
⑴.
.
⑵
=
=112(cm3)
112
初试身手
4.如图所示,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
解:
设AB=a,AD=b,A′A=c,
则长方体ABCD-A′B′C′D′的体积V=abc
又,且三棱锥C-A′DD′为CD=a,
∴.
∴剩余部分几何体体积.
则=1:5.
课堂小结
棱柱、棱锥、棱台的表面积和体积
表面积
体积
各个面的面积的和
V棱锥= Sh
V棱台
V棱柱=Sh
S'=S
S'=0
作业布置
作业: P119-120 习题8. 第1,2,3,6题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第七章
8.3 简单几何体的表面积和体积
人教A版(2019)
前面我们分别认识了基本立体图形的结构特征和平面表示,本节进一步认识简单几何体的表面积和体积. 表面积是几何体表面的面积,它表示几何体表面的大小,体积是几何体所占空间的大小.
第七章
8.3.1 棱柱、棱锥、棱台的表面积和体积
人教A版(2019)
教学目标
学习目标 数学素养
1.了解棱柱、棱锥、棱台的表面积和体积计算公式. 1.数学运算素养.
2.理解并掌握侧面展开图与几何体的表面积之间的关系,并能运用计算公式求几何体的表面积和体积. 2.数学抽象素养.
温故知新
矩形面积:
S=ab
a
b
三角形面积:
a
h
B
C
A
c
平行四边形面积:
a
b
A
梯形面积:
a
b
h
圆的面积:
r
扇形面积:
r
圆心角为n°
正三角形的面积:
a
正方形面积:
a
温故知新
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
长方体、正方体表面积
展开图
平面图形面积
空间问题
平面问题
知新探究
多面体的表面积就是围成多面体各个面的面积的和.棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.
棱柱的表面积
=2 底面积+侧面积
棱锥的表面积
=底面积+侧面积
棱台的表面积
=上底面积+下底面积+侧面积
棱柱、棱锥、棱台的表面积
知新探究
【例1】如图,四面体P-ABC的各棱长均为a,求它的表面积.
分析:因为四面体的四个面是全等的等边三角形,所以四面体的表面积等于其中任何一个面的面积的4倍.
棱柱、棱锥、棱台的表面积
B
C
A
P
解:
∵△PBC是正三角形,其边长为a,
∴.
因此,四面体P-ABC的表面积
.
知新探究
棱柱、棱锥、棱台的体积
我们以前已经学习了特殊棱柱——正方体、长方体的体积公式,
它们分别是
V正方体=a3(a是正方体的棱长)
V长方体=abc(a,b,c分别是长方体的长、宽、高)
a
c
知新探究
棱柱、棱锥、棱台的体积
一般地,如果棱柱的底面面积为S,高为h,那么这个棱柱的体积
V棱柱=Sh
棱柱的高
棱柱的高是指两底面之间的距离,即从一底面上任意一点向另一个底面作垂线,这点与垂足之间的距离.
知新探究
棱柱、棱锥、棱台的体积
关于体积有如下几个原理:
⑴相同的几何体的体积相等;
⑵一个几何体的体积等于它的各部分体积之和;
⑶等底面积等高的两个同类几何体的体积相等;
⑷体积相等的两个几何体叫做等积体.
知新探究
棱柱、棱锥、棱台的体积
将一个三棱柱按如图所示分解成三个三棱锥,那么这三个三棱锥的体积有什么关系?它们与三棱柱的体积有什么关系?
1
2
3
1
2
3
Sh
Sh
知新探究
棱柱、棱锥、棱台的体积
推广到一般的棱锥,你猜想锥体的体积公式是什么?
高h
底面积S
如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍.
因此,一般地,如果棱锥的底面面积为S,高为h,那么该棱锥的体积
.
棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.
知新探究
棱柱、棱锥、棱台的体积
由于棱台是由棱锥截成的,因此可以利用两个棱锥的体积差,得到棱台的体积公式
棱台的高
.
其中S′,S分别为棱台的上、下底面面积,h为棱台的高.
棱台的高是指两底面之间的距离,即从上底面上任意一点向下底面作垂线,这点与垂足之间的距离.
知新探究
棱柱、棱锥、棱台的体积
观察棱柱、棱锥、棱台的体积公式:
,,.
它们之间有什么关系 你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗
V棱柱=Sh
V棱锥= Sh
V棱台
上底扩大
S'=S
S'=S
S'=0
上底缩小
S'=0
知新探究
【例2】如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5cm,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米(精确到0.01立方米)?(计算漏斗的容积时不考虑漏斗的厚度)
分析:漏斗由两个多面体组成,其容积就是两个多面体的体积.
知新探究
【例2】如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5cm,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米(精确到0.01立方米)?(计算漏斗的容积时不考虑漏斗的厚度)
解:
由题意知
(m3).
(m3).
所以这个漏斗的容积
(m3)
初试身手
1.侧面都是等腰直角三角形的正三棱锥,底面边长为a,则该棱锥的表面积是( )
A. B. C. D.
解:
设正三棱锥的侧棱长为b,则由已知条件知,b2+b2=a2,,
∴,
故选A.
初试身手
2.已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,则该四棱台的表面积为 .
解:
如图,在四棱台ABCD-A1B1C1D1中,过B1作B1F BC,垂足为F,
在Rt△B1FB中,BF=,B1B=8,
∴B1F=.
∴.
∴四棱台的表面积S=
=.
初试身手
3.⑴如图,底面为矩形的四棱锥P-ABCD,PA为四棱锥的高,PA=AB=1,BC=2,则四棱锥P-ABCD的体积为 .
⑵已知有一正四棱台的上底边长为4cm,下底边长为8cm,高为3cm,
则其体积为 cm3.
解:
⑴.
.
⑵
=
=112(cm3)
112
初试身手
4.如图所示,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
解:
设AB=a,AD=b,A′A=c,
则长方体ABCD-A′B′C′D′的体积V=abc
又,且三棱锥C-A′DD′为CD=a,
∴.
∴剩余部分几何体体积.
则=1:5.
课堂小结
棱柱、棱锥、棱台的表面积和体积
表面积
体积
各个面的面积的和
V棱锥= Sh
V棱台
V棱柱=Sh
S'=S
S'=0
作业布置
作业: P119-120 习题8. 第1,2,3,6题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
