数学人教A版(2019)必修第二册6.1平面向量的概念 课件(共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册6.1平面向量的概念 课件(共24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
6.1平面向量的概念
6.1.1向量的实际背景与概念
6.1.2向量的几何表示
6.1.3相等向量与共线向量
第六章 平面向量及其应用
人教版A版必修第二册
学习目标
1.了解平面向量的实际背景,理解平面向量的概念;
2.掌握平面向量的表示方法,理解向量的模的概念;
3.理解零向量、单位向量、相等向量、共线向量的概念.
探究一:老鼠为什么认为猫是傻猫?
创设情境
10m/s
傻猫
50m/s
猫的速度再快也没用,因为方向错了
速度是既有大小又有方向的量
A
创设情境
从A点到B点的位移
探究二:
像速度这种既有大小又有方向的量,在物理中你还学过哪些呢?
东
西
北
南
45o
拍打篮球的力
一、向量的概念
新知学习
1.向量
既有大小,又有方向的量叫做向量(物理学中称为矢量)
2.数量
只有大小,没有方向的量叫做数量(物理学中称为标量)
注:向量只与大小和方向有关
一、向量的概念
新知学习
概念辨析练习:
判断以下量是向量还是数量。
1.重力 ( )
2.年龄 ( )
3.加速度 ( )
4.距离 ( )
5.弹力 ( )
6.温度 ( )
7.身高 ( )
向量
数量
向量
数量
向量
数量
数量
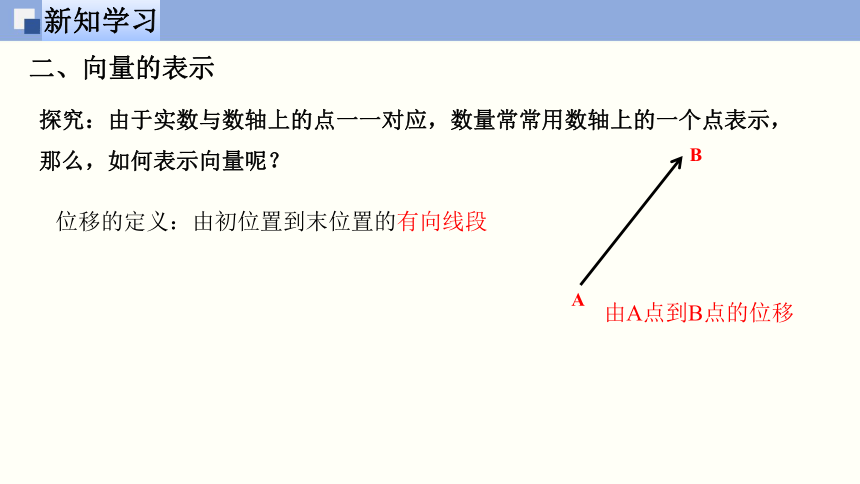
二、向量的表示
新知学习
探究:由于实数与数轴上的点一一对应,数量常常用数轴上的一个点表示,那么,如何表示向量呢?
A
位移的定义:由初位置到末位置的有向线段
B
由A点到B点的位移
二、向量的表示
新知学习
在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,就说线段AB具有方向
具有方向的线段叫做有向线段,记作:
有向线段三要素:起点、方向、长度
A(起点)
B(终点)
二、向量的表示
新知学习
几何表示:用有向线段表示,记作
字母表示:用字母表示
注:印刷时用黑体表示,书写时用表示
二、向量的表示
新知学习
思考:向量可以用有向线段表示,那是否可以认为有向线段就是向量?
有向线段的三要素:起点、方向、长度
向量:可选任意点作为向量的起点、有大小、有方向
A
B
C
D
A
B
C
D
有向线段、是不同的
向量、是同一个向量
有向线段不是向量
二、向量的表示
新知学习
向量的大小如何表示?
有向线段的长度表示向量的大小
向量的大小称为向量的长度(或称模)记作
二、向量的表示
新知学习
思考1:若,,则 ,该结论是否正确?
不正确,两个向量不能比较大小,但两个向量的模可以比较大小
无意义,有意义
思考2:向量的模可以为0吗?可以为1吗?可以为负数吗?
可以为0、1,但大小不能为负数
零向量:长度为0的向量,记作0
单位向量:长度等于1个单位的向量
注:零向量的方向是任意的,单位向量的方向具体而定
二、向量的表示
新知学习
思考3:平面直角坐标系内,起点在原点O的单位向量,它们的终点的轨迹是什么图形?
O
x
y
单位圆
三 、相等向量与共线向量
新知学习
互动探究:在纸上画出如图所示的向量
(1)图中哪些向量是单位向量?
(2),,三个向量的方向之间有何关系
(3,在大小和方向上有何关系?
A
B
C
F
D
N
E
M
H
G
一个单位
(1),,,
(2)、方向相同,与方向相反
(3),大小相等,方向相同
三 、相等向量与共线向量
新知学行向量:方向相同或相反的非零向量叫做平行向量
平行,记为
A
B
C
F
D
N
E
M
H
G
一个单位
任一组平行向量都可以平移到同一条直线上
平行向量也叫做共线向量
规定:零向量与任一向量平行
对于任意向量,都有
直线AB与CD平行或重合
新知学习
思考:若则直线AB与CD的关系是什么?
三 、相等向量与共线向量
A
B
C
D
A
B
C
D
三 、相等向量与共线向量
新知学习
相等向量:方向相同且长度相等的向量叫做相等向量. 相等,记为
A
B
C
F
D
N
E
M
H
G
一个单位
相反向量:方向 且长度 的向量叫做相反向量.
相反,记为
相反
相等
解:(1) ,是共线向量
,,是共线向量
,,,是共线向量
新知学习
(课本P4)例2改编.如图,设O是正六边形ABCDEF的中心,
(1)写出图中与、、的共线向量;
(2)分别写出图中与向量、、相等的向量.
(2)
三 、相等向量与共线向量
解:
(1)与的模相等,且方向相反的向量有
新知学习
跟踪训练.如图,已知四边形ABCD为平行四边形,
则:
(1)与的模相等,且方向相反的向量有哪些?
(2)写出与共线的向量
三 、相等向量与共线向量
(2)与共线的向量有,,
C
达标训练
1.设,是两个单位向量,则下列说法正确的是( )
A.
B.
C.
D. 以上都不对
B
达标训练
2.如图所示,梯形ABCD为等腰梯形,则两腰上的向量与的关系是( )
A.
B.
C.
D.
课堂小结
向量
定义
长度(模)
表示
几何表示法:有向线段
字母表示法:
零向量
单位向量
向量间的关系
相等向量
平行(共线)向量
向量的有关概念
特殊向量
有大小、有方向、能自由平移
相反向量
课堂小结
课后作业
完成课时作业(一)A组、B组
下 课
6.1平面向量的概念
6.1.1向量的实际背景与概念
6.1.2向量的几何表示
6.1.3相等向量与共线向量
第六章 平面向量及其应用
人教版A版必修第二册
学习目标
1.了解平面向量的实际背景,理解平面向量的概念;
2.掌握平面向量的表示方法,理解向量的模的概念;
3.理解零向量、单位向量、相等向量、共线向量的概念.
探究一:老鼠为什么认为猫是傻猫?
创设情境
10m/s
傻猫
50m/s
猫的速度再快也没用,因为方向错了
速度是既有大小又有方向的量
A
创设情境
从A点到B点的位移
探究二:
像速度这种既有大小又有方向的量,在物理中你还学过哪些呢?
东
西
北
南
45o
拍打篮球的力
一、向量的概念
新知学习
1.向量
既有大小,又有方向的量叫做向量(物理学中称为矢量)
2.数量
只有大小,没有方向的量叫做数量(物理学中称为标量)
注:向量只与大小和方向有关
一、向量的概念
新知学习
概念辨析练习:
判断以下量是向量还是数量。
1.重力 ( )
2.年龄 ( )
3.加速度 ( )
4.距离 ( )
5.弹力 ( )
6.温度 ( )
7.身高 ( )
向量
数量
向量
数量
向量
数量
数量
二、向量的表示
新知学习
探究:由于实数与数轴上的点一一对应,数量常常用数轴上的一个点表示,那么,如何表示向量呢?
A
位移的定义:由初位置到末位置的有向线段
B
由A点到B点的位移
二、向量的表示
新知学习
在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,就说线段AB具有方向
具有方向的线段叫做有向线段,记作:
有向线段三要素:起点、方向、长度
A(起点)
B(终点)
二、向量的表示
新知学习
几何表示:用有向线段表示,记作
字母表示:用字母表示
注:印刷时用黑体表示,书写时用表示
二、向量的表示
新知学习
思考:向量可以用有向线段表示,那是否可以认为有向线段就是向量?
有向线段的三要素:起点、方向、长度
向量:可选任意点作为向量的起点、有大小、有方向
A
B
C
D
A
B
C
D
有向线段、是不同的
向量、是同一个向量
有向线段不是向量
二、向量的表示
新知学习
向量的大小如何表示?
有向线段的长度表示向量的大小
向量的大小称为向量的长度(或称模)记作
二、向量的表示
新知学习
思考1:若,,则 ,该结论是否正确?
不正确,两个向量不能比较大小,但两个向量的模可以比较大小
无意义,有意义
思考2:向量的模可以为0吗?可以为1吗?可以为负数吗?
可以为0、1,但大小不能为负数
零向量:长度为0的向量,记作0
单位向量:长度等于1个单位的向量
注:零向量的方向是任意的,单位向量的方向具体而定
二、向量的表示
新知学习
思考3:平面直角坐标系内,起点在原点O的单位向量,它们的终点的轨迹是什么图形?
O
x
y
单位圆
三 、相等向量与共线向量
新知学习
互动探究:在纸上画出如图所示的向量
(1)图中哪些向量是单位向量?
(2),,三个向量的方向之间有何关系
(3,在大小和方向上有何关系?
A
B
C
F
D
N
E
M
H
G
一个单位
(1),,,
(2)、方向相同,与方向相反
(3),大小相等,方向相同
三 、相等向量与共线向量
新知学行向量:方向相同或相反的非零向量叫做平行向量
平行,记为
A
B
C
F
D
N
E
M
H
G
一个单位
任一组平行向量都可以平移到同一条直线上
平行向量也叫做共线向量
规定:零向量与任一向量平行
对于任意向量,都有
直线AB与CD平行或重合
新知学习
思考:若则直线AB与CD的关系是什么?
三 、相等向量与共线向量
A
B
C
D
A
B
C
D
三 、相等向量与共线向量
新知学习
相等向量:方向相同且长度相等的向量叫做相等向量. 相等,记为
A
B
C
F
D
N
E
M
H
G
一个单位
相反向量:方向 且长度 的向量叫做相反向量.
相反,记为
相反
相等
解:(1) ,是共线向量
,,是共线向量
,,,是共线向量
新知学习
(课本P4)例2改编.如图,设O是正六边形ABCDEF的中心,
(1)写出图中与、、的共线向量;
(2)分别写出图中与向量、、相等的向量.
(2)
三 、相等向量与共线向量
解:
(1)与的模相等,且方向相反的向量有
新知学习
跟踪训练.如图,已知四边形ABCD为平行四边形,
则:
(1)与的模相等,且方向相反的向量有哪些?
(2)写出与共线的向量
三 、相等向量与共线向量
(2)与共线的向量有,,
C
达标训练
1.设,是两个单位向量,则下列说法正确的是( )
A.
B.
C.
D. 以上都不对
B
达标训练
2.如图所示,梯形ABCD为等腰梯形,则两腰上的向量与的关系是( )
A.
B.
C.
D.
课堂小结
向量
定义
长度(模)
表示
几何表示法:有向线段
字母表示法:
零向量
单位向量
向量间的关系
相等向量
平行(共线)向量
向量的有关概念
特殊向量
有大小、有方向、能自由平移
相反向量
课堂小结
课后作业
完成课时作业(一)A组、B组
下 课
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
