物理人教版(2019)选择性必修第一册2.4单摆(共44张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册2.4单摆(共44张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 88.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-27 22:45:55 | ||
图片预览







文档简介
(共44张PPT)
第二章 机械振动
§2.4 单摆
人教版 高中物理选择性必修一
目录
单摆的回复力
02
单摆的周期
03
单摆的应用
04
单摆
01
巩固练习
05
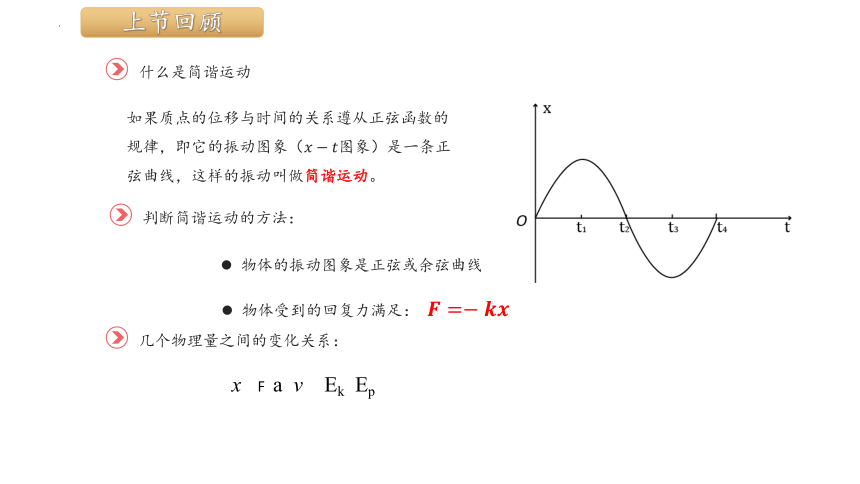
如果质点的位移与时间的关系遵从正弦函数的规律,即它的振动图象(图象)是一条正弦曲线,这样的振动叫做简谐运动。
物体的振动图象是正弦或余弦曲线
判断简谐运动的方法:
物体受到的回复力满足:
什么是简谐运动
上节回顾
几个物理量之间的变化关系:
x F a v Ek Ep
新课引入
单摆
摆长:悬点到球心的距离 L=L0+R球
构成:一根不可伸长的细线下面悬挂一个小球就构成了单摆。
摆角:摆到最高点时,摆线与竖直方向的夹角θ。
摆 角
θ
摆球质量m
摆长 L=L0+R球
摆线长 L0
思考:什么是单摆
悬点
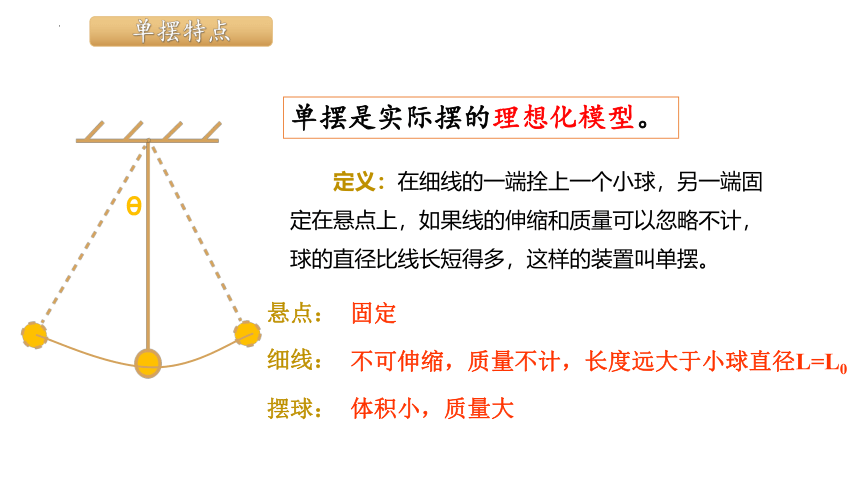
单摆是实际摆的理想化模型。
定义:在细线的一端拴上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略不计,球的直径比线长短得多,这样的装置叫单摆。
悬点:
不可伸缩,质量不计,长度远大于小球直径L=L0
固定
细线:
摆球:
体积小,质量大
单摆特点
θ
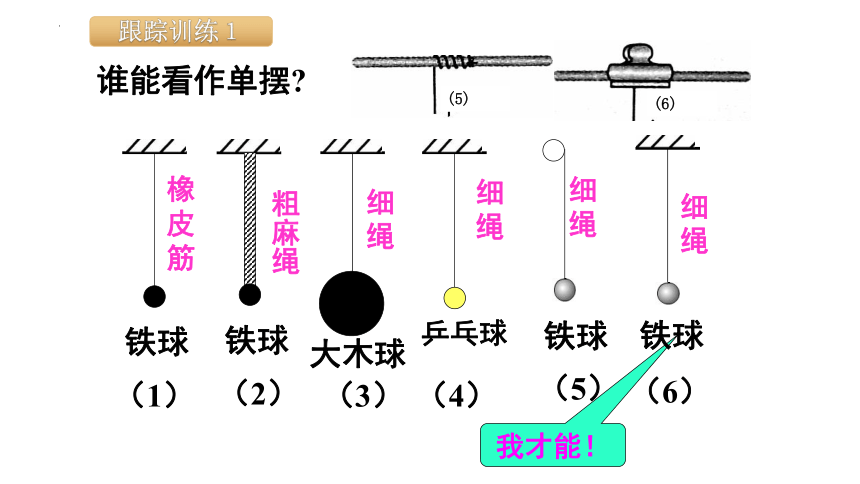
谁能看作单摆
我才能!
铁球
(1)
橡皮筋
粗麻绳
铁球
(2)
大木球
(3)
乒乓球
细绳
(4)
细绳
铁球
(5)
细绳
(6)
铁球
(5)
(6)
细绳
跟踪训练1
方法一:根据回复力的规律F=-kx 判断
方法二:根据物体的振动图像 判断
思考2
如何若判断单摆振动是不是简谐运动?用什么方法判断?
单摆的回复力
F
F
B
A
O
方向:
沿切线指向平衡位置
P
θ
T
G
G2
G1
重力沿切线的分力提供回复力
回复力大小:
向心力大小:
方向:
沿半径指向悬点
与该点速度方向在同一直线上,不断改变速度大小
与该点速度方向垂直,只改变速度方向
单摆的回复力
(1)任意位置
(2)平衡位置
摆球经过平衡位置时,G2=G,G1=0,此时F应大于G,F-G提供向心力,
因此,在平衡位置,回复力F回=0,与G1=0相符.
(3)单摆的简谐运动
在θ很小时(理论值为<5°),
G1= = ,
G1方向与摆球位移方向相反,所以有回复力F回=
因此,在摆角θ很小时,单摆做简谐运动.
单摆的回复力
跟踪训练2
摆角θ 正弦值 弧度值
1° 0.01754 0.01745
2° 0.03490 0.03491
3° 0.05234 0.05236
4° 0.06976 0.06981
5° 0.08716 0.08727
6° 0.10453 0.10472
7° 0.12187 0.12217
8° 0.13917 0.13963
在摆角小于5度的条件下:Sinθ≈θ(弧度值)
单摆的回复力
x
当θ很小时,x≈弧长
F=G1=mgsinθ
位移方向与回复力方向相反
摆角θ<5°的单摆运动可认为是简谐运动
单摆的回复力
(1)所谓平衡位置,是指摆球静止时,摆线拉力与小球所受重力平衡的位置,并不是指摆动过程中的受力平衡位置.实际上,在摆动过程中,摆球受力不可能平衡.
(2)回复力是由摆球受到的重力沿圆弧切线方向的分力 提供的,不可误认为回复力是重力G与摆线拉力T的合力.
对于单摆的两点说明
单摆的回复力
单摆的受力特点
(1)单摆振动的回复力为摆球重力沿圆弧切线方向的分力,回复力不是摆球所受的合外力.当摆球摆至平衡位置时,回复力等于零,合外力提供向心力.
(2)单摆的运动不一定是简谐运动,只有在摆角较小的情况下才能看成简谐运动,理论上一般θ角不超过5°,但在实验中,摆角很小时单摆运动的细节不易观察清楚,带来的测量误差反而会增大,因此实验中一般θ角不超过10°.
一般规律1
单摆的回复力
单摆的运动特点:
(1)摆线以悬点为圆心做变速圆周运动,因此在运动过程中只要速度v≠0,半径方向都受向心力.
(2)摆线同时以平衡位置为中心做往复运动,因此在运动过程中只要不在平衡位置,轨迹的切线方向都受回复力.
一般规律2
单摆的回复力
总结
1、回复力的来源
摆球的重力沿圆弧切线方向的分力。
2、回复力的特点
在偏角很小时,摆球所受的回复力与它偏离平衡位置的位移成正比,方向总指向平衡位置,即F= 。
单摆的回复力
分析单摆运动时其对平衡位置
位移、回复力、加速度、速度在一次全振动中的变化?
减小
增大
减小
增大
速度
增大
减小
增大
减小
加速度
增大
减小
增大
减小
回复力
增大
减小
增大
减小
对平衡位置的位移
O→A′
A—O
O—A
A′→O
单摆的运动
思考讨论3
单摆的振动图像
如图,细线下悬挂一个除去了柱塞的注射器,注射器内装上墨汁。当注射器摆动时,沿着垂直于摆动的方向匀速拖动木板,观察喷在木板上的墨汁图样。
单摆的振动图像
综上,在摆角很小的情况下,单摆做简谐振动。
结论:单摆振动的x-t图象是一条正弦(余弦)函数图像。
单摆的振动图像
(多选)关于单摆摆球在运动过程中的受力,下列结论正确的是( )
A.摆球受重力、摆线的拉力作用
B.摆球受重力、摆线的拉力、回复力作用
C.摆球的回复力为零时,向心力最大
D.摆球的回复力最大时,摆线中的拉力大小比摆球的重力大
解析:单摆在运动过程中,摆球受重力和摆线的拉力,重力沿圆弧切线的分力提供回复力,故A对、B错;在平衡位置处,回复力为零,速度最大,向心力最大,选项C正确;当回复力最大时,摆球在最大位移处,速度为零,向心力为零,则拉力等于重力沿半径方向的分力,即拉力小于重力,选项D错误。
AC
跟踪训练3
单摆的周期
猜想?
振幅
质量
摆长
重力加速度
摆角θ很小时,单摆做的是简谐运动,单摆的周期与什么因素有相关呢?
思考讨论4:
单摆的周期
F
F
摆球质量相同,振幅相同,观察周期T与摆长l的关系?
1、实验方法:控制变量法
摆长l相同,摆角相同,观察周期T与摆球质量的关系?
摆球质量相同,摆长l相同,观察周期T与振幅的关系?
单摆的周期的探究
在同一个地方,单摆周期T与摆球质量和振幅无关,仅与摆长 l 有关系,且摆长越长,周期越大。
荷兰物理学家惠更斯(1629---1695)通过实验进一步得到:
单摆做简谐运动的周期T与摆长L的二次方根成正比,与重力加速度g的二次方根成反比,与振幅、摆球质量无关.
2、实验结论
单摆的周期公式:
单摆的周期的探究
小球振动周期很短
傅科摆周期很长
猜想:
1.单摆的周期与振幅有关
2.单摆的周期与摆球的质量有关
3.单摆的周期与摆长有关
1.影响单摆周期的因素
(1)单摆的周期与摆球质量、振幅无关.
(2)单摆的周期与摆长有关,摆长越长,周期越大.
单摆的等时性:单摆的周期与振幅无关的性质.
单摆的运动是一种简谐运动,其图像的意义、摆球的运动过程与弹簧振子的运动分析相似,只是摆球运动中还受向心力的作用.
单摆的周期的探究
2.周期公式
(1)公式的提出:周期公式是荷兰物理学家惠更斯首先提出的。
(2)公式:T=2π ,即T与摆长l的二次方根成正比,与重力加速度g的二次方根成反比。
周期公式的应用:由单摆周期公式可得g= ,只要测出单摆的摆长l和周期T就可算出当地的重力加速度。
3.单摆周期公式的理解和应用
1.对公式 的理解由公式 知,某单摆做简谐运动(摆角小于
5°)的周期只与其摆长l和当地的重力加速度g有关,而与振幅或摆球质量无关,故又叫做单摆的固有周期.
(1)摆长l:实际的单摆摆球不可能是质点,所以摆长应是从悬点到摆球球心的长度,即 ,l1为摆线长,d为摆球直径.
3.单摆周期公式的理解和应用
(2)重力加速度g
①若单摆系统只处在重力场中且处于静止状态,g由单摆所处的空间位置决定,即g= ,式中R为物体到地心的距离,M为地球的质量,g随所在地表的位置和高度的变化而变化.
②在不同星球上M和R一般不同,g也不同,g=9.8 m/s2只是在地球表面附近时的取值.
单摆的应用
F
F
(1)计时器:利用等时性
惠更斯在1656年首先利用摆的等时性发明了带摆的计时器(1657年获得专利权)。
周期T =2s的单摆叫做秒摆
(2)测定当地的重力加速度
3. 单摆周期的应用
测出单摆的摆长和周期就可求重力加速度
科学漫步
从日晷到原子钟
我国制造的空间冷原子钟
日晷
课堂总结
1、单摆的理想化模型:在细线的一端拴上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略不计,球的直径比线长短得多。
2、单摆运动的性质:在摆角 < 10°的条件下,单摆的振动可看作简谐振动。
3、单摆振动的周期公式 :
单摆周期与摆长和重力加速度有关,与振幅和质量无关。
巩固练习
1、(多选)关于单摆摆球在运动过程中的受力,下列结论正确的是( )
A.摆球受重力、摆线的张力作用
B.摆球的回复力最大时,向心力为零
C.摆球的回复力为零时,向心力最大
D.摆球的回复力最大时,摆线中的张力大小比摆球的重力大
E.摆球的向心力最大时,摆球的加速度方向沿摆球的运动方向
ABC
例、(单选)有一个正在摆动的秒摆(T=2 s),若取摆球正从平衡位置向左运动时开始计时,那么当t=1.6 s时,以下对摆球的运动情况及回复力变化情况正确的是
( )
A.正在向左做减速运动,回复力正在增大
B.正在向右做减速运动,回复力正在增大
C.正在向右做加速运动,回复力正在减小
D.正在向左做加速运动,回复力正在减小
D
3、一个摆长为2 m的单摆,在地球上某地振动时,测得完成100次全振动所用的时间为284 s。
(1)求当地的重力加速度g的大小。
(2)把该单摆拿到月球上去,已知月球上的重力加速度是1.60 m/s2,则该单摆振动周期是多少
答案:(1)9.78 m/s2 (2)7.02 s
1、(多选)单摆是为研究振动而抽象出的理想化模型,其理想化条件是( )
A.摆线质量不计
B.摆线长度不伸缩
C.摆球的直径比摆线长度短得多
D.只要是单摆的运动就是一种简谐运动
解析:单摆由摆线和摆球组成,摆线只计长度不计质量,摆球只计质量不计大小,且摆线不伸缩,选项A、B、C正确。但把单摆作为简谐运动来处理是有条件的,只有在摆角很小的情况下才能视单摆的运动为简谐运动,选项D错误。
ABC
2、下列关于单摆的说法正确的是( )
A.单摆摆球从平衡位置运动到正向最大位移处时的位移为A(A为振幅),从正向最大位移处运动到平衡位置时的位移为-A
B.单摆摆球的回复力等于摆球所受的合外力
C.单摆摆球的回复力等于摆球重力沿圆弧切线方向的分力
D.单摆摆球经过平衡位置时加速度为零
解析:简谐运动中的位移是以平衡位置作为起点,摆球在正向最大位移处时位移为A,在平衡位置时位移应为零。摆球的回复力由重力沿圆弧切线方向的分力提供,线的拉力与重力沿摆线方向的分力的合力提供向心力,摆球经最低点(振动的平衡位置)时回复力为零,但向心力不为零,所以合外力不为零;摆球到最高点时,向心力为零,回复力最大,合外力也不为零。
C
3、将秒摆(周期为2 s的单摆)的周期变为4 s,下面哪些措施是正确的( )
A.只将摆球质量变为原来的
B.只将振幅变为原来的2倍
C.只将摆长变为原来的4倍
D.只将摆长变为原来的16倍
C
第二章 机械振动
§2.4 单摆
人教版 高中物理选择性必修一
目录
单摆的回复力
02
单摆的周期
03
单摆的应用
04
单摆
01
巩固练习
05
如果质点的位移与时间的关系遵从正弦函数的规律,即它的振动图象(图象)是一条正弦曲线,这样的振动叫做简谐运动。
物体的振动图象是正弦或余弦曲线
判断简谐运动的方法:
物体受到的回复力满足:
什么是简谐运动
上节回顾
几个物理量之间的变化关系:
x F a v Ek Ep
新课引入
单摆
摆长:悬点到球心的距离 L=L0+R球
构成:一根不可伸长的细线下面悬挂一个小球就构成了单摆。
摆角:摆到最高点时,摆线与竖直方向的夹角θ。
摆 角
θ
摆球质量m
摆长 L=L0+R球
摆线长 L0
思考:什么是单摆
悬点
单摆是实际摆的理想化模型。
定义:在细线的一端拴上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略不计,球的直径比线长短得多,这样的装置叫单摆。
悬点:
不可伸缩,质量不计,长度远大于小球直径L=L0
固定
细线:
摆球:
体积小,质量大
单摆特点
θ
谁能看作单摆
我才能!
铁球
(1)
橡皮筋
粗麻绳
铁球
(2)
大木球
(3)
乒乓球
细绳
(4)
细绳
铁球
(5)
细绳
(6)
铁球
(5)
(6)
细绳
跟踪训练1
方法一:根据回复力的规律F=-kx 判断
方法二:根据物体的振动图像 判断
思考2
如何若判断单摆振动是不是简谐运动?用什么方法判断?
单摆的回复力
F
F
B
A
O
方向:
沿切线指向平衡位置
P
θ
T
G
G2
G1
重力沿切线的分力提供回复力
回复力大小:
向心力大小:
方向:
沿半径指向悬点
与该点速度方向在同一直线上,不断改变速度大小
与该点速度方向垂直,只改变速度方向
单摆的回复力
(1)任意位置
(2)平衡位置
摆球经过平衡位置时,G2=G,G1=0,此时F应大于G,F-G提供向心力,
因此,在平衡位置,回复力F回=0,与G1=0相符.
(3)单摆的简谐运动
在θ很小时(理论值为<5°),
G1= = ,
G1方向与摆球位移方向相反,所以有回复力F回=
因此,在摆角θ很小时,单摆做简谐运动.
单摆的回复力
跟踪训练2
摆角θ 正弦值 弧度值
1° 0.01754 0.01745
2° 0.03490 0.03491
3° 0.05234 0.05236
4° 0.06976 0.06981
5° 0.08716 0.08727
6° 0.10453 0.10472
7° 0.12187 0.12217
8° 0.13917 0.13963
在摆角小于5度的条件下:Sinθ≈θ(弧度值)
单摆的回复力
x
当θ很小时,x≈弧长
F=G1=mgsinθ
位移方向与回复力方向相反
摆角θ<5°的单摆运动可认为是简谐运动
单摆的回复力
(1)所谓平衡位置,是指摆球静止时,摆线拉力与小球所受重力平衡的位置,并不是指摆动过程中的受力平衡位置.实际上,在摆动过程中,摆球受力不可能平衡.
(2)回复力是由摆球受到的重力沿圆弧切线方向的分力 提供的,不可误认为回复力是重力G与摆线拉力T的合力.
对于单摆的两点说明
单摆的回复力
单摆的受力特点
(1)单摆振动的回复力为摆球重力沿圆弧切线方向的分力,回复力不是摆球所受的合外力.当摆球摆至平衡位置时,回复力等于零,合外力提供向心力.
(2)单摆的运动不一定是简谐运动,只有在摆角较小的情况下才能看成简谐运动,理论上一般θ角不超过5°,但在实验中,摆角很小时单摆运动的细节不易观察清楚,带来的测量误差反而会增大,因此实验中一般θ角不超过10°.
一般规律1
单摆的回复力
单摆的运动特点:
(1)摆线以悬点为圆心做变速圆周运动,因此在运动过程中只要速度v≠0,半径方向都受向心力.
(2)摆线同时以平衡位置为中心做往复运动,因此在运动过程中只要不在平衡位置,轨迹的切线方向都受回复力.
一般规律2
单摆的回复力
总结
1、回复力的来源
摆球的重力沿圆弧切线方向的分力。
2、回复力的特点
在偏角很小时,摆球所受的回复力与它偏离平衡位置的位移成正比,方向总指向平衡位置,即F= 。
单摆的回复力
分析单摆运动时其对平衡位置
位移、回复力、加速度、速度在一次全振动中的变化?
减小
增大
减小
增大
速度
增大
减小
增大
减小
加速度
增大
减小
增大
减小
回复力
增大
减小
增大
减小
对平衡位置的位移
O→A′
A—O
O—A
A′→O
单摆的运动
思考讨论3
单摆的振动图像
如图,细线下悬挂一个除去了柱塞的注射器,注射器内装上墨汁。当注射器摆动时,沿着垂直于摆动的方向匀速拖动木板,观察喷在木板上的墨汁图样。
单摆的振动图像
综上,在摆角很小的情况下,单摆做简谐振动。
结论:单摆振动的x-t图象是一条正弦(余弦)函数图像。
单摆的振动图像
(多选)关于单摆摆球在运动过程中的受力,下列结论正确的是( )
A.摆球受重力、摆线的拉力作用
B.摆球受重力、摆线的拉力、回复力作用
C.摆球的回复力为零时,向心力最大
D.摆球的回复力最大时,摆线中的拉力大小比摆球的重力大
解析:单摆在运动过程中,摆球受重力和摆线的拉力,重力沿圆弧切线的分力提供回复力,故A对、B错;在平衡位置处,回复力为零,速度最大,向心力最大,选项C正确;当回复力最大时,摆球在最大位移处,速度为零,向心力为零,则拉力等于重力沿半径方向的分力,即拉力小于重力,选项D错误。
AC
跟踪训练3
单摆的周期
猜想?
振幅
质量
摆长
重力加速度
摆角θ很小时,单摆做的是简谐运动,单摆的周期与什么因素有相关呢?
思考讨论4:
单摆的周期
F
F
摆球质量相同,振幅相同,观察周期T与摆长l的关系?
1、实验方法:控制变量法
摆长l相同,摆角相同,观察周期T与摆球质量的关系?
摆球质量相同,摆长l相同,观察周期T与振幅的关系?
单摆的周期的探究
在同一个地方,单摆周期T与摆球质量和振幅无关,仅与摆长 l 有关系,且摆长越长,周期越大。
荷兰物理学家惠更斯(1629---1695)通过实验进一步得到:
单摆做简谐运动的周期T与摆长L的二次方根成正比,与重力加速度g的二次方根成反比,与振幅、摆球质量无关.
2、实验结论
单摆的周期公式:
单摆的周期的探究
小球振动周期很短
傅科摆周期很长
猜想:
1.单摆的周期与振幅有关
2.单摆的周期与摆球的质量有关
3.单摆的周期与摆长有关
1.影响单摆周期的因素
(1)单摆的周期与摆球质量、振幅无关.
(2)单摆的周期与摆长有关,摆长越长,周期越大.
单摆的等时性:单摆的周期与振幅无关的性质.
单摆的运动是一种简谐运动,其图像的意义、摆球的运动过程与弹簧振子的运动分析相似,只是摆球运动中还受向心力的作用.
单摆的周期的探究
2.周期公式
(1)公式的提出:周期公式是荷兰物理学家惠更斯首先提出的。
(2)公式:T=2π ,即T与摆长l的二次方根成正比,与重力加速度g的二次方根成反比。
周期公式的应用:由单摆周期公式可得g= ,只要测出单摆的摆长l和周期T就可算出当地的重力加速度。
3.单摆周期公式的理解和应用
1.对公式 的理解由公式 知,某单摆做简谐运动(摆角小于
5°)的周期只与其摆长l和当地的重力加速度g有关,而与振幅或摆球质量无关,故又叫做单摆的固有周期.
(1)摆长l:实际的单摆摆球不可能是质点,所以摆长应是从悬点到摆球球心的长度,即 ,l1为摆线长,d为摆球直径.
3.单摆周期公式的理解和应用
(2)重力加速度g
①若单摆系统只处在重力场中且处于静止状态,g由单摆所处的空间位置决定,即g= ,式中R为物体到地心的距离,M为地球的质量,g随所在地表的位置和高度的变化而变化.
②在不同星球上M和R一般不同,g也不同,g=9.8 m/s2只是在地球表面附近时的取值.
单摆的应用
F
F
(1)计时器:利用等时性
惠更斯在1656年首先利用摆的等时性发明了带摆的计时器(1657年获得专利权)。
周期T =2s的单摆叫做秒摆
(2)测定当地的重力加速度
3. 单摆周期的应用
测出单摆的摆长和周期就可求重力加速度
科学漫步
从日晷到原子钟
我国制造的空间冷原子钟
日晷
课堂总结
1、单摆的理想化模型:在细线的一端拴上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略不计,球的直径比线长短得多。
2、单摆运动的性质:在摆角 < 10°的条件下,单摆的振动可看作简谐振动。
3、单摆振动的周期公式 :
单摆周期与摆长和重力加速度有关,与振幅和质量无关。
巩固练习
1、(多选)关于单摆摆球在运动过程中的受力,下列结论正确的是( )
A.摆球受重力、摆线的张力作用
B.摆球的回复力最大时,向心力为零
C.摆球的回复力为零时,向心力最大
D.摆球的回复力最大时,摆线中的张力大小比摆球的重力大
E.摆球的向心力最大时,摆球的加速度方向沿摆球的运动方向
ABC
例、(单选)有一个正在摆动的秒摆(T=2 s),若取摆球正从平衡位置向左运动时开始计时,那么当t=1.6 s时,以下对摆球的运动情况及回复力变化情况正确的是
( )
A.正在向左做减速运动,回复力正在增大
B.正在向右做减速运动,回复力正在增大
C.正在向右做加速运动,回复力正在减小
D.正在向左做加速运动,回复力正在减小
D
3、一个摆长为2 m的单摆,在地球上某地振动时,测得完成100次全振动所用的时间为284 s。
(1)求当地的重力加速度g的大小。
(2)把该单摆拿到月球上去,已知月球上的重力加速度是1.60 m/s2,则该单摆振动周期是多少
答案:(1)9.78 m/s2 (2)7.02 s
1、(多选)单摆是为研究振动而抽象出的理想化模型,其理想化条件是( )
A.摆线质量不计
B.摆线长度不伸缩
C.摆球的直径比摆线长度短得多
D.只要是单摆的运动就是一种简谐运动
解析:单摆由摆线和摆球组成,摆线只计长度不计质量,摆球只计质量不计大小,且摆线不伸缩,选项A、B、C正确。但把单摆作为简谐运动来处理是有条件的,只有在摆角很小的情况下才能视单摆的运动为简谐运动,选项D错误。
ABC
2、下列关于单摆的说法正确的是( )
A.单摆摆球从平衡位置运动到正向最大位移处时的位移为A(A为振幅),从正向最大位移处运动到平衡位置时的位移为-A
B.单摆摆球的回复力等于摆球所受的合外力
C.单摆摆球的回复力等于摆球重力沿圆弧切线方向的分力
D.单摆摆球经过平衡位置时加速度为零
解析:简谐运动中的位移是以平衡位置作为起点,摆球在正向最大位移处时位移为A,在平衡位置时位移应为零。摆球的回复力由重力沿圆弧切线方向的分力提供,线的拉力与重力沿摆线方向的分力的合力提供向心力,摆球经最低点(振动的平衡位置)时回复力为零,但向心力不为零,所以合外力不为零;摆球到最高点时,向心力为零,回复力最大,合外力也不为零。
C
3、将秒摆(周期为2 s的单摆)的周期变为4 s,下面哪些措施是正确的( )
A.只将摆球质量变为原来的
B.只将振幅变为原来的2倍
C.只将摆长变为原来的4倍
D.只将摆长变为原来的16倍
C
