四川省凉山州民族中学2023-2024学年高二下学期3月月考数学试题(PDF版,含解析)
文档属性
| 名称 | 四川省凉山州民族中学2023-2024学年高二下学期3月月考数学试题(PDF版,含解析) |

|
|
| 格式 | |||
| 文件大小 | 461.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 00:00:00 | ||
图片预览



文档简介
绝密★启用前
2023-2024 学年度高二数学 3 月月考试题
考试时间:120 分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第 I卷(选择题)
一、单选题(每小题 5 分,共 40 分)
1.已知集合 A x x2 2x 0 ,B x x sin kπ , k Z ,则 A B ( )
2
A. 1,0 B. 0,1 C. 0 D. 1
1 2i
2.已知复数 z满足 z ,则其共轭复数
2 i z
( )
5 i 5A. i B. i C. D. i
3 3
3.等比数列 an 的各项均为正数,且 a5a6 a4a7 18,则 log3 a1 log3 a2 log3 a10
( )
A.12 B.10 C.5 D. 2 log3 5
4.已知 a 2,且 a b 2,则向量b在向量 a上的投影向量为( )
1 a 1
r
A. B. b C. a D.2 2 b
5.若 cos
π 1
,则 sin2 ( )
4 3
5 5 7 7
A. B. C. D.
9 9 9 9
6.函数 f x 的图象如图所示,下列数值排序正确的是 ( )
A.0 f 2 f 3 f 3 f 2 B.0 f 3 f 3 f 2 f 2
C.0 f 3 f 2 f 3 f 2 D.0 f 3 f 2 f 2 f 3
7.函数 f x ln 2x 1 x2 x的单调递增区间是( )
试卷第 1页,共 4页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
1
A. 0,1 B ,1 . 2
1 2
C. ,
1 2 1 ,1 2
2 2
D.
2 2
8.如图,长方体 ABCD A1B1C1D1中,AB BC 1,AA1 2,M为 AA1的中点,过B1M
作长方体的截面 交棱CC1于 N,下列正确的是( )
①截面 可能为六边形
②存在点 N,使得 BN 截面
③若截面 为平行四边形,则1 CN 2
N C 3 6④当 与 重合时,截面面积为
4
A.①② B.③④ C.①③ D.②④
二、多选题(每小题 5 分,共 20 分,少选 3 分,错选 0 分,全对 5 分)
9.下列求导运算正确的是( )
1
A. ln 7
7
B. x2 2 sin x
2xsin x x2 2 cos x
C x
2 2x x2
. x x
e e
D. ln 3x 2
1
3x 2
10.下列函数中是奇函数且在 0, 上单调递增的是( )
1
A. y x3 B. y x3
C. y ex D. y ln x
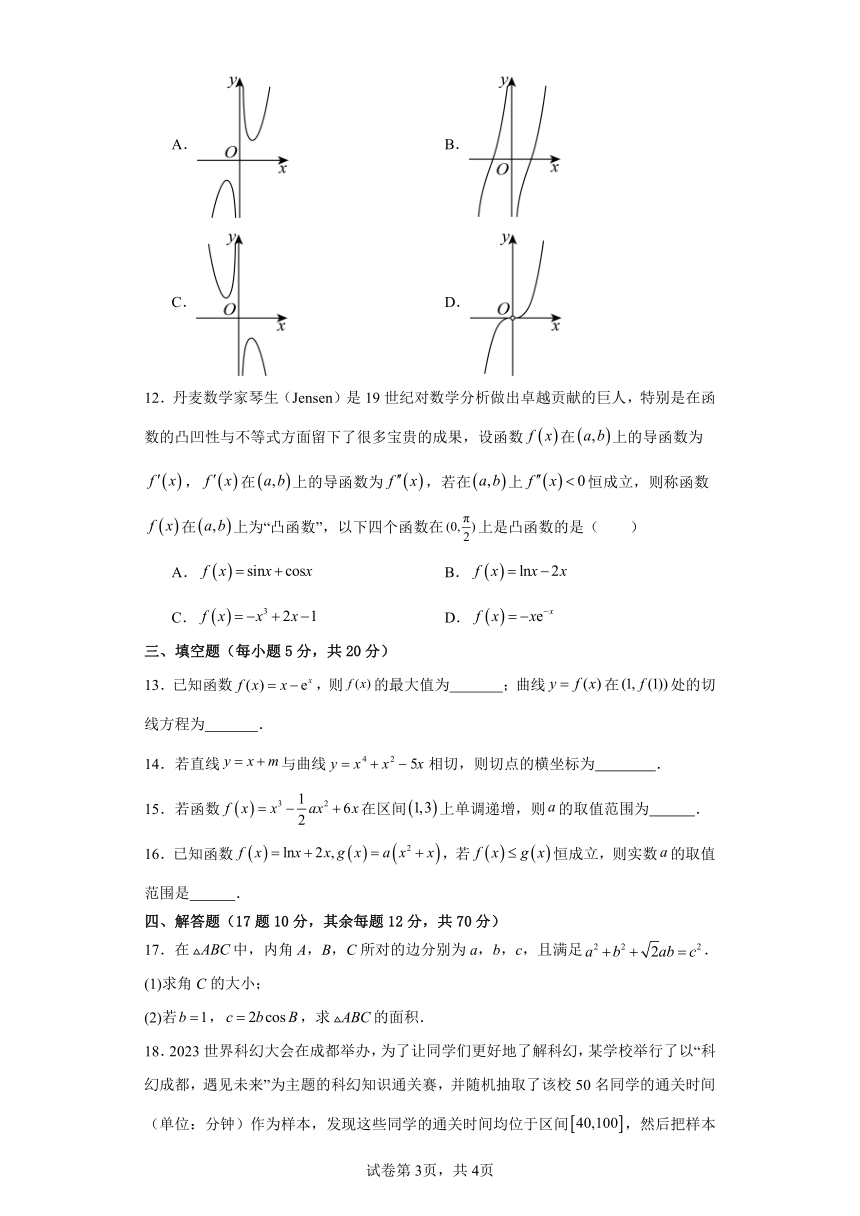
11 f x x3 m.函数 m R 的图象可能是( )
x
试卷第 2页,共 4页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
A. B.
C. D.
12.丹麦数学家琴生(Jensen)是 19世纪对数学分析做出卓越贡献的巨人,特别是在函
数的凸凹性与不等式方面留下了很多宝贵的成果,设函数 f x 在 a,b 上的导函数为
f x , f x 在 a,b 上的导函数为 f x ,若在 a,b 上 f x 0恒成立,则称函数
f x 在 a,b 上为“凸函数”,以下四个函数在 (0, π )2 上是凸函数的是( )
A. f x sinx cosx B. f x lnx 2x
C. f x x3 2x 1 D x. f x xe
三、填空题(每小题 5 分,共 20 分)
13.已知函数 f (x) x ex,则 f (x)的最大值为 ;曲线 y f (x)在 (1, f (1))处的切
线方程为 .
14.若直线 y x m与曲线 y x 4 x 2 5x 相切,则切点的横坐标为 .
15.若函数 f x x3 1 ax2 6x在区间 1,3 上单调递增,则 a的取值范围为 .
2
16 2.已知函数 f x lnx 2x, g x a x x ,若 f x g x 恒成立,则实数 a的取值
范围是 .
四、解答题(17 题 10 分,其余每题 12 分,共 70 分)
17.在 ABC中,内角 A,B,C所对的边分别为 a,b,c,且满足 a2 b2 2ab c2.
(1)求角 C的大小;
(2)若b 1, c 2bcosB,求 ABC的面积.
18.2023世界科幻大会在成都举办,为了让同学们更好地了解科幻,某学校举行了以“科
幻成都,遇见未来”为主题的科幻知识通关赛,并随机抽取了该校 50名同学的通关时间
(单位:分钟)作为样本,发现这些同学的通关时间均位于区间 40,100 ,然后把样本
试卷第 3页,共 4页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
数据分成 40,50 , 50,60 , 60,70 , 70,80 , 80,90 , 90,100 六组,经过整理绘
制成频率分布直方图(如图所示).
(1)计算 a的值,并估算该校同学通关时间低于 60分钟的概率;
(2)拟在通关时间低于 60分钟的样本数据对应的同学中随机选取 2位同学赠送科幻大会
入场券,求此 2人的通关时间均位于区间 50,60 的概率.
n n 119 .已知数列 an 的前 n项和为 Sn .2
(1)求数列 an 的通项公式 an ;
(2)记b
1
n a a ,求数列 bn 的前 n项和.n n 1
2 2
20 x y.已知椭圆 C: 2 b 02 1( a 0, )的长轴为 4 3,短轴长为 4.a b
(1)求椭圆 C的标准方程;
(2)设直线 l:y x m与椭圆 C交于不同两点 A、B,且 AB 3 2,求直线 AB的方程.
21.在正四棱柱 ABCD A1B1C1D1中,AA1 2AB 4,点 E在线段CC1上,且CC1 4CE,
点 F 为 BD中点.
(1)求点D1到直线 EF 的距离;
(2)求证: A1C 面BDE .
22.已知函数 f x ax 2lnx .
(1)讨论函数 f x 的单调区间;
(2)当 x 0时, f x 1 x3 x2 2 2ex 2lnx恒成立,求实数 a的取值范围.
2
试卷第 4页,共 4页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
参考答案:
1.B
【分析】求出集合A,对整数 k的取值进行讨论,可求得集合 B,利用交集的定义可求得集
合 A B .
2
【详解】因为 A x x 2x 0 x 0 x 2 ,
kπ
对于 x sin k Z ,当 k 4n n Z 时, x sin kπ sin 2nπ 0,
2 2
当 k 4n 1 n Z 时, x sin kπ π π sin 2nπ
sin 1,2 2 2
当 k 4n 2 n Z 时, x sin kπ sin 2nπ π sin π 0,
2
当 k 4n 3 n Z x sin kπ sin 时, 2nπ
3π
sin
3π
1,
2 2 2
B x x sin kπ 综上所述, ,k Z 1,0,1 ,
2
因此, A B 0,1 .
故选:B.
2.B
【分析】由复数除法以及共轭复数的概念即可得解.
1 2i 2 i 5
【详解】因为 z i i 2 i 2 i 5 ,所以 z i .
故选:B.
3.B
【分析】利用等比数列的性质,结合对数的运算法则即可得解.
【详解】因为 an 是各项均为正数的等比数列,a5a6 a4a7 18,
所以 a5a6 a4a7 2a5a6 18,即 a5a6 9,则 a1a10 a2a9 a5a6 9
记 S log3 a1 log3 a2 log3 a10,则 S log3 a10 log3 a9 log3 a1,
两式相加得 2S log 3 a1a10 log 3 a2a9 log 3 a10a1
log3 a1a10 log3 a2a9 log3 a10a1 10 log3 9 20 ,
所以 S 10,即 log3 a1 log3 a2 log3 a10 10 .
答案第 1页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
故选:B.
4.C
【分析】根据向量在向量上的投影公式进行计算即可.
a b a 2 a
【详解】因为向量b在向量 a上的投影向量为: aa a ,2 2
故选:C.
5.C
【分析】根据二倍角公式以及诱导公式即可求解.
cos π 1 π cos 2 π 7【详解】由 可得4 3
2 =2cos 1 ,
2 4 9
cos 2 π 故 =sin 2
7
,
2 9
故选:C
6.B
【分析】利用导数的几何意义,结合函数的图象,即可判断选项.
【详解】由函数 f x 的图象可知:
当 x 0时, f x 单调递增,且增速变缓慢,
f
3 f 2
f 3 f 2 ,表示 AB直线的斜率,
3 2
根据导数的几何意义可知,0 f 3 f 3 f 2 f 2 ,
故选:B
7.D
【分析】求出函数的定义域与导函数,再令 f (x) > 0,解得即可.
【详解】函数 f x ln 2x 1 x2 x 1 的定义域为 , ,
2
答案第 2页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
2 2 2x 1 2 2 2x 1 2 2x 1 且 f x 2x 1 ,
2x 1 2x 1 2x 1
f (x) > 0 1 x 1 2令 ,解得 ,
2 2
1 1 2
所以 f x 的单调递增区间为 ,2 2 .
故选:D
8.B
【分析】
利用点 N的位置不同得到的截面的形状判断选项 A,C,利用线面垂直的判定定理分析选项
B,利用平面几何知识求相应的量结合梯形的面积公式求得截面的面积,从而可判断选项 D.
【详解】长方体 ABCD A1B1C1D1中,过B1M作长方体的截面 交棱CC1于 N,
设N0为CC1的中点,根据点 N的位置的变化分析可得,
当1 CN 2时,截面 为平行四边形,
当0 CN 1时,截面 为五边形,
当CN 0,即点 N与点 C重合时,截面 为梯形,故①错误,③正确;
设BN 截面 ,因为 B1M ,所以 BN B1M,
又 A1B1 平面 BCC1B1,且 BN 平面 BCC1B1,所以 BN A1B1,
又 A1B1 B1M B1,所以BN 平面 ABB1A1,
所以 N只能与 C重合才能使 BN B1M,
因为 BN 显然不垂直平面 B1CQM ,故此时不成立,故②错误;
因为当 N与 C重合时,截面 为梯形,
如图 (2)所示,过 M作MM 垂直于 B1C于点M ,
答案第 3页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
设梯形的高为 h, B1M x,
2 2
2 5 5
则由平面几何知识可得 h2 2 x2 x ,
2 2
解得 x 2 5 ,h 30 ,
5 5
5
5 所以截面 的面积为 2 30 3 6 ,故④正确.
2 5 4
故选:B.
9.BC
【分析】根据导数的四则运算以及复合函数的导数,即可判断选项.
【详解】 ln 7 0,故 A错误;
x2 2 sin x 2xsin x x2 2 cos x,故 B正确;
x2 2x e x x2e x 2x x2
,故 C正确;ex
e 2x
ex
ln 3x 2
3
,故 D错误.3x 2
故选:BC
10.AB
【分析】AB选项,根据幂函数的性质得到 AB正确;C选项,不满足奇偶性;D选项,不
满足单调性.
【详解】A选项, y x3为奇函数且在 R上单调递增,满足要求,A正确;
1 1 1 1
B选项, g x x 3 的定义域为 R,且 g x x 3 x 3 g x ,故 g x x 3 为奇函数,
1 1
又 0,故
3 g x x
3 在 0, 单调递增,B正确;
C选项, y ex 为指数函数,结合图象可知其不是奇函数,C错误;
答案第 4页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
ln x,0 x 1
D选项, y ln x ,故当0 x 1时, y lnxln x, x 1 单调递减,D错误.
故选:AB
11.ABD
【分析】利用分类讨论及函数的单调性与导数的关系,结合函数的性质即可求解.
【详解】由题意可知,函数 f x 的定义域为 ,0 0, ,
m
当m 0时, f x 2x2 2 0,函数 f x 在 ,0 , 0, 上单调递增,故 B正确;x
当m 0时, f x x3, f x 2x 0,所以在 ,0 , 0, 上单调递增,故 D正确;
当m 0时,当 x 0时, f x x3 m 0 3 m;当 x 0时, f x x 0;
x x
故 A正确;C错误.
故选:ABD.
12.ABC
【分析】根据凸函数的定义,求导,即可根据二阶导数的正负判断.
【详解】对于 A,由 f x sinx cosx,得 f x =cosx-sinx,则
f x sinx cosx sinx cosx x (0, π=- + ,因为 ),所以
2
sin x 0,cos x 0, f x - sinx+cosx 0,所以此函数是凸函数;
对于 B,由 f x lnx 2x ,得 f x 1 2,则 f x 1 π2 ,因为 x (0, ),所以x x 2
f x 1 2 0,所以此函数是凸函数;x
C f x =-x3对于 ,由 2x 1,得 f x =-3x2 2,则 f x 6x,因为 x (0, π),所以
2
f x 6x 0,所以此函数是凸函数;
x x -x x x x x
对于 D,由 f x =-xe ,得 f x =-e xe ,则 f x e e -xe = 2 x e ,因为
x (0, π) f x 2 x e x,所以 0,所以此函数不是凸函数,
2
故选:ABC
13. 1 y (1 e)x
【分析】求出函数的导数,判断函数单调性,即可求得答案;根据导数的几何意义即可求得
答案第 5页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
曲线 y f (x)在 (1, f (1))处的切线方程.
【详解】由 f (x) x ex可得 f (x) 1 ex,
当 x 0时, f (x) 0,当 x 0时, f (x) 0,
故 f (x)在 ( , 0)上单调递增,在 (0, )上单调递减,
故 f (x)max f (0) 1;
由 f (1) 1 e,f (1) 1 e,
故曲线 y f (x)在 (1, f (1))处的切线方程为 y 1 e (1 e)(x 1),
即 y (1 e)x,
故答案为: 1; y (1 e)x
14.1
【分析】求出函数的导函数,令 f x 4x 3 2x 5,再利用导数说明函数的单调性,由
f 1 1,即可得到方程 4x3 2x 5 1的解,从而得解.
【详解】因为 y x 4 x 2 5x ,所以 y 4x3 2x 5,
f x 4x 3设函数 2x 5 2,则 f x 12x 2 0,
所以 f x 4x 3 2x 5在定义域R 上单调递增,
因为 f 1 1,所以方程 4x3 2x 5 1的解为 x 1,则所求切点的横坐标为1.
故答案为:1
15. ,6 2
3 1 2
【分析】函数 f x x ax 6x在区间 1,3 上单调递增,转化为 f x 0在 1,3 上恒成
2
立,即 a
6
3x 恒成立,利用基本不等式求最值可得答案.
x
1
【详解】因为 f x x3 ax2 6x,
2
所以 f x 3x2 ax 6,
3 1 2
因为函数 f x x ax 6x在区间 1,3 上单调递增,
2
所以 f x 3x2 ax 6 0在 1,3 上恒成立,
答案第 6页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
即 x 1,3 6时, a 3x 恒成立,
x
3x 6因为 2 3x 6 =6 2,当且仅当 x 2时等号成立,
x x
6
即 3x x
6 2,所以 a 6 2,
min
故答案为: ,6 2 .
16.[1, )
【分析】根据题意,构造函数 F(x) f (x) g(x)
1
,分 a 0与a 0 讨论,然后转化为F 0
a
恒成立,代入计算,即可得到结果.
【详解】构造函数 F(x) f (x) g(x),其定义域为 (0, ),
F (x) 1 (2x 1)(ax 1)则 2 2ax a , x (0, ),
x x
当a 0时, F (x) 0, f (x)单调递增,F 1 2 2a 0,F x 0不可能恒成立;
1 1
当a 0时,令 F (x) 0,得 x 或 x (舍去).
a 2
0 1当 x 时, F (x) 0;
a
x 1
1
当 时, F (x) 0,故 F (x)在 (0, )上有最大值 F ,
a a
F 1 0 1 1由题意知 恒成立,即 ln 1 0,
a a a
1 1
令 (a) ln 1,则 (a)在 (0, )上单调递减,且 (1) 0,
a a
1 1
故 ln 1 0成立的充要条件是 a 1.
a a
故答案为:[1, )
3π
17.(1)C
4
(2) 2
4
【分析】(1)根据余弦定理,即可求解;
(2)根据正弦定理以及二倍角公式,得到角和边的关系,再结合三角形的面积公式,即可
求解.
2
1 cosC a b
2 c2 2ab 2
【详解】( ) ,且C 0, π ,
2ab 2ab 2
答案第 7页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
所以C
3π
;
4
(2)根据正弦定理, c 2b cos B sinC 2sin B cos B sin 2B,
所以C 2B或C 2B π,
3π 3π
当C 2B时,C ,B ,此时B C π,不成立,
4 8
π
当C 2B π时,此时 A B ,则 a b 1,
8
ABC 1的面积 S ab sinC 1 1 1 2 2 .
2 2 2 4
18.(1)a 0.006,0.1
(2)0.3
【分析】(1)根据频率分布直方图的性质,求得 a 0.006,进而得到估计该校同学通关时
间低于钟的概率;
(2)根据题意得到通关时间位于区间 50,60 和 40,50 的人数,利用列举法求得基本事件
的总数,以及所求事件中包含的基本事件的个数,结合古典摡型的概率计算公式,即可求解.
【详解】(1)解:因为 0.004 a 0.018 0.022 2 0.028 10 1,所以 a 0.006,
由所给频率分布直方图可知,50名同学通关时间低于钟的频率为 0.004 0.006 10 0.1,
据此估计该校同学通关时间低于钟的概率为0.1 .
(2)解:样本中同学通关时间位于区间 50,60 的有50 0.006 10 3人,即为 A1, A2 , A3,
通关时间位于区间 40,50 的有:50 0.004 10 2(位),即为 B1, B2,
从这 5名入样同学中随机抽取 2人,所有可能的结果共有 10种,
分别为 A1, A2 , A1,A3 , A1,B1 , A1,B2 , A2 , A3 , A2 ,B1 , A2 ,B2 , A3 ,B1 , A3,B2 ,
B1,B2 ,
所抽取 2人的通关时间均位于区间 50,60 的结果有 3种,即 A1, A2 , A1,A3 , A2 , A3 ,
3
故此 2人的通关时间均位于区间 50,60 的概率为 P 0.3.
10
19.(1)an n
答案第 8页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
n
(2)
n 1
【分析】
S1,n 1
(1)根据 an S S ,n 2作差即可得解; n n 1
1 1
(2)由(1)可得bn ,利用裂项相消法计算可得.n n 1
【详解】(1) n
n(n 1)
数列的前 项和为 Sn ,2
1
n 1 a 1 1 当 时 1 S1 1,2
n
n 2 S n 1 当 时 n 1 ,2
n(n 1) n(n 1)
所以 an Sn Sn 1 n,2 2
又当 n 1时, an n也成立,
数列 an 的通项公式为 an n .
1 1 1 1
(2)由(1)可得bn a a ,n n 1 n n 1 n n 1
设数列 bn 的前 n项和为Tn,
则Tn b1 b2 b3 bn
1 1 1 1 1 1 1 1 1 1 n .
2 2 3 3 4 n n 1 n 1 n 1
2
20 x y
2
.(1) 1
12 4
(2) y x 2
【分析】(1)由长轴长和短轴长可得椭圆方程;
(2)联立直线方程与椭圆方程,利用韦达定理和弦长公式即可求得 m的值,则直线 AB的
方程可求.
【详解】(1)由已知长轴为 4 3,短轴长为 4,
可得 a 2 3,b 2,
答案第 9页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
2 2
则椭圆 C x y的标准方程为: 1;
12 4
y x m
(2)依题意 x2 y2 ,
1 12 4
解得 4x2 6mx 3m2 12 0,
因为 0,可得 4 m 4,
x1 x
3m
2
2
且 ,
x x 3m
2 12
1 2
4
2
因为 AB 1 k 2 x 9m1 x 2
2 4x1x
2
2 2 3m 124 3 2 ,
解得m 2,
所以直线 AB的方程为 l: y x 2.
21.(1) 114
3
(2)证明见解析
【分析】(1)依题建系,求得相关点和向量的坐标,利用点到直线的距离的空间向量计算公
式即可求得;
(2)由(1)中所建的系求出 A1C,DB,DE的坐标,分别计算得到 A1C DB 0和 A1C DE 0,
由线线垂直推出线面垂直.
【详解】(1)
如图,以D为原点,以DA,DC,DD1分别为 x, y, z轴正方向,建立空间直角坐标系,
正四棱柱 ABCD A1B1C1D1 , AA1 2AB 4,CC1 4CE,F 为 BD中点,
答案第 10页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
D1 0,0,4 ,E 0,2,1 ,F 1,1,0 ,ED1 0, 2,3 ,EF 1 , 1, 1
2
2
D 2EF d ED ED1 EF 13 1 114则点 1到直线 的距离为: 1 .
EF
3 3
(2)由(1)可得C 0,2,0 ,B 2,2,0 , A1 2,0,4 ,
则 A1C 2,2, 4 ,DB 2,2,0 ,DE 0,2,1 ,
由 A1C DB 2 2 2 2 0 可得 A1C DB,
又由 A1C DE 2 2 ( 4) 1 0可得 A1C DE,
又DB DE D,
故 A1C 面BDE .
22.(1)答案见解析
7
(2)a 2e
2
【分析】(1)对函数 f x 求导,分别讨论a 0和 a 0两种情况,即可求出结果;
x x
(2 1 2 2e)先分离参数,将原式化为 a x2 x ,构造函数 g x 1 x2 x 2 2e ,
2 x x 2 x x
利用导数判断 g x 的单调性进而求出 g x 的最大值即可.
【详解】(1) f x 的定义域为 0,+ , f x =a 2 ax 2 ,
x x
当a 0时, f (x) 0恒成立,所以 f x 的单调递减区间为 0,+ ,
当a 0时,令 f (x) 0
2 2
,则 x ,所以 f x 的单调递增区间为 , ,
a a
令 f (x) 0 0 x
2 2
,则
,所以 f x 的单调递减区间为 0, ,a a
综上:当 a 0时, f x 的单调递减区间为 0,+ ,无增区间;
当a 0时, f x 2 2 的单调递增区间为 , ,单调递减区间为 0, ;
a a
2 x 0 f x 1 x3 x2 2 2ex( )当 时, 2lnx恒成立,
2
即ax 2lnx
1
x3 x2 2 2ex 2lnx对 x 0恒成立,
2
答案第 11页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
a 1 x2 x 2 2e
x
即 对 x 0恒成立,
2 x x
g x 1 2 2e
x
令 x2 x ( x 0),
2 x x
g x x 1 2 2 x 1 e
x x3 x2 2 2 x 1 ex
x2 x2 x2
x 1 x2 2x 2 2 x 1 ex x 1 x2 2x 2 2ex
2 x x2
令m x x2 2x 2 2ex( x 0),则m (x) 2x 2 2ex,
令 t x m (x) 2x 2 2e x( x 0),则 t (x) 2 2ex,
由 x 0得, ex 1,所以 t (x) 0,所以 t x 在 0,+ 上单调递减,
所以 t x t 0 0,即m (x) 0,所以m x 在 0,+ 上单调递减,
所以m x m 0 0,
令 g (x) 0,则 0 x 1,所以 g x 在 0,1 单调递增,
令 g (x) 0,则 x 1,所以 g x 在 1, 单调递减,
所以 g x g 1 7 2e 7 ,所以 a 2e .
2 2
综上实数 a的取值范围为 a
7
2e .
2
1 2 2ex
【点睛】关键点点睛:本题第二问的关键是分离参数得 a x2 x 对 x 0恒成立,
2 x x
1 x
再设新函数 g x x2 x 2 2e ( x 0),对此求导研究其最值即可.
2 x x
答案第 12页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
2023-2024 学年度高二数学 3 月月考试题
考试时间:120 分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第 I卷(选择题)
一、单选题(每小题 5 分,共 40 分)
1.已知集合 A x x2 2x 0 ,B x x sin kπ , k Z ,则 A B ( )
2
A. 1,0 B. 0,1 C. 0 D. 1
1 2i
2.已知复数 z满足 z ,则其共轭复数
2 i z
( )
5 i 5A. i B. i C. D. i
3 3
3.等比数列 an 的各项均为正数,且 a5a6 a4a7 18,则 log3 a1 log3 a2 log3 a10
( )
A.12 B.10 C.5 D. 2 log3 5
4.已知 a 2,且 a b 2,则向量b在向量 a上的投影向量为( )
1 a 1
r
A. B. b C. a D.2 2 b
5.若 cos
π 1
,则 sin2 ( )
4 3
5 5 7 7
A. B. C. D.
9 9 9 9
6.函数 f x 的图象如图所示,下列数值排序正确的是 ( )
A.0 f 2 f 3 f 3 f 2 B.0 f 3 f 3 f 2 f 2
C.0 f 3 f 2 f 3 f 2 D.0 f 3 f 2 f 2 f 3
7.函数 f x ln 2x 1 x2 x的单调递增区间是( )
试卷第 1页,共 4页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
1
A. 0,1 B ,1 . 2
1 2
C. ,
1 2 1 ,1 2
2 2
D.
2 2
8.如图,长方体 ABCD A1B1C1D1中,AB BC 1,AA1 2,M为 AA1的中点,过B1M
作长方体的截面 交棱CC1于 N,下列正确的是( )
①截面 可能为六边形
②存在点 N,使得 BN 截面
③若截面 为平行四边形,则1 CN 2
N C 3 6④当 与 重合时,截面面积为
4
A.①② B.③④ C.①③ D.②④
二、多选题(每小题 5 分,共 20 分,少选 3 分,错选 0 分,全对 5 分)
9.下列求导运算正确的是( )
1
A. ln 7
7
B. x2 2 sin x
2xsin x x2 2 cos x
C x
2 2x x2
. x x
e e
D. ln 3x 2
1
3x 2
10.下列函数中是奇函数且在 0, 上单调递增的是( )
1
A. y x3 B. y x3
C. y ex D. y ln x
11 f x x3 m.函数 m R 的图象可能是( )
x
试卷第 2页,共 4页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
A. B.
C. D.
12.丹麦数学家琴生(Jensen)是 19世纪对数学分析做出卓越贡献的巨人,特别是在函
数的凸凹性与不等式方面留下了很多宝贵的成果,设函数 f x 在 a,b 上的导函数为
f x , f x 在 a,b 上的导函数为 f x ,若在 a,b 上 f x 0恒成立,则称函数
f x 在 a,b 上为“凸函数”,以下四个函数在 (0, π )2 上是凸函数的是( )
A. f x sinx cosx B. f x lnx 2x
C. f x x3 2x 1 D x. f x xe
三、填空题(每小题 5 分,共 20 分)
13.已知函数 f (x) x ex,则 f (x)的最大值为 ;曲线 y f (x)在 (1, f (1))处的切
线方程为 .
14.若直线 y x m与曲线 y x 4 x 2 5x 相切,则切点的横坐标为 .
15.若函数 f x x3 1 ax2 6x在区间 1,3 上单调递增,则 a的取值范围为 .
2
16 2.已知函数 f x lnx 2x, g x a x x ,若 f x g x 恒成立,则实数 a的取值
范围是 .
四、解答题(17 题 10 分,其余每题 12 分,共 70 分)
17.在 ABC中,内角 A,B,C所对的边分别为 a,b,c,且满足 a2 b2 2ab c2.
(1)求角 C的大小;
(2)若b 1, c 2bcosB,求 ABC的面积.
18.2023世界科幻大会在成都举办,为了让同学们更好地了解科幻,某学校举行了以“科
幻成都,遇见未来”为主题的科幻知识通关赛,并随机抽取了该校 50名同学的通关时间
(单位:分钟)作为样本,发现这些同学的通关时间均位于区间 40,100 ,然后把样本
试卷第 3页,共 4页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
数据分成 40,50 , 50,60 , 60,70 , 70,80 , 80,90 , 90,100 六组,经过整理绘
制成频率分布直方图(如图所示).
(1)计算 a的值,并估算该校同学通关时间低于 60分钟的概率;
(2)拟在通关时间低于 60分钟的样本数据对应的同学中随机选取 2位同学赠送科幻大会
入场券,求此 2人的通关时间均位于区间 50,60 的概率.
n n 119 .已知数列 an 的前 n项和为 Sn .2
(1)求数列 an 的通项公式 an ;
(2)记b
1
n a a ,求数列 bn 的前 n项和.n n 1
2 2
20 x y.已知椭圆 C: 2 b 02 1( a 0, )的长轴为 4 3,短轴长为 4.a b
(1)求椭圆 C的标准方程;
(2)设直线 l:y x m与椭圆 C交于不同两点 A、B,且 AB 3 2,求直线 AB的方程.
21.在正四棱柱 ABCD A1B1C1D1中,AA1 2AB 4,点 E在线段CC1上,且CC1 4CE,
点 F 为 BD中点.
(1)求点D1到直线 EF 的距离;
(2)求证: A1C 面BDE .
22.已知函数 f x ax 2lnx .
(1)讨论函数 f x 的单调区间;
(2)当 x 0时, f x 1 x3 x2 2 2ex 2lnx恒成立,求实数 a的取值范围.
2
试卷第 4页,共 4页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
参考答案:
1.B
【分析】求出集合A,对整数 k的取值进行讨论,可求得集合 B,利用交集的定义可求得集
合 A B .
2
【详解】因为 A x x 2x 0 x 0 x 2 ,
kπ
对于 x sin k Z ,当 k 4n n Z 时, x sin kπ sin 2nπ 0,
2 2
当 k 4n 1 n Z 时, x sin kπ π π sin 2nπ
sin 1,2 2 2
当 k 4n 2 n Z 时, x sin kπ sin 2nπ π sin π 0,
2
当 k 4n 3 n Z x sin kπ sin 时, 2nπ
3π
sin
3π
1,
2 2 2
B x x sin kπ 综上所述, ,k Z 1,0,1 ,
2
因此, A B 0,1 .
故选:B.
2.B
【分析】由复数除法以及共轭复数的概念即可得解.
1 2i 2 i 5
【详解】因为 z i i 2 i 2 i 5 ,所以 z i .
故选:B.
3.B
【分析】利用等比数列的性质,结合对数的运算法则即可得解.
【详解】因为 an 是各项均为正数的等比数列,a5a6 a4a7 18,
所以 a5a6 a4a7 2a5a6 18,即 a5a6 9,则 a1a10 a2a9 a5a6 9
记 S log3 a1 log3 a2 log3 a10,则 S log3 a10 log3 a9 log3 a1,
两式相加得 2S log 3 a1a10 log 3 a2a9 log 3 a10a1
log3 a1a10 log3 a2a9 log3 a10a1 10 log3 9 20 ,
所以 S 10,即 log3 a1 log3 a2 log3 a10 10 .
答案第 1页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
故选:B.
4.C
【分析】根据向量在向量上的投影公式进行计算即可.
a b a 2 a
【详解】因为向量b在向量 a上的投影向量为: aa a ,2 2
故选:C.
5.C
【分析】根据二倍角公式以及诱导公式即可求解.
cos π 1 π cos 2 π 7【详解】由 可得4 3
2 =2cos 1 ,
2 4 9
cos 2 π 故 =sin 2
7
,
2 9
故选:C
6.B
【分析】利用导数的几何意义,结合函数的图象,即可判断选项.
【详解】由函数 f x 的图象可知:
当 x 0时, f x 单调递增,且增速变缓慢,
f
3 f 2
f 3 f 2 ,表示 AB直线的斜率,
3 2
根据导数的几何意义可知,0 f 3 f 3 f 2 f 2 ,
故选:B
7.D
【分析】求出函数的定义域与导函数,再令 f (x) > 0,解得即可.
【详解】函数 f x ln 2x 1 x2 x 1 的定义域为 , ,
2
答案第 2页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
2 2 2x 1 2 2 2x 1 2 2x 1 且 f x 2x 1 ,
2x 1 2x 1 2x 1
f (x) > 0 1 x 1 2令 ,解得 ,
2 2
1 1 2
所以 f x 的单调递增区间为 ,2 2 .
故选:D
8.B
【分析】
利用点 N的位置不同得到的截面的形状判断选项 A,C,利用线面垂直的判定定理分析选项
B,利用平面几何知识求相应的量结合梯形的面积公式求得截面的面积,从而可判断选项 D.
【详解】长方体 ABCD A1B1C1D1中,过B1M作长方体的截面 交棱CC1于 N,
设N0为CC1的中点,根据点 N的位置的变化分析可得,
当1 CN 2时,截面 为平行四边形,
当0 CN 1时,截面 为五边形,
当CN 0,即点 N与点 C重合时,截面 为梯形,故①错误,③正确;
设BN 截面 ,因为 B1M ,所以 BN B1M,
又 A1B1 平面 BCC1B1,且 BN 平面 BCC1B1,所以 BN A1B1,
又 A1B1 B1M B1,所以BN 平面 ABB1A1,
所以 N只能与 C重合才能使 BN B1M,
因为 BN 显然不垂直平面 B1CQM ,故此时不成立,故②错误;
因为当 N与 C重合时,截面 为梯形,
如图 (2)所示,过 M作MM 垂直于 B1C于点M ,
答案第 3页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
设梯形的高为 h, B1M x,
2 2
2 5 5
则由平面几何知识可得 h2 2 x2 x ,
2 2
解得 x 2 5 ,h 30 ,
5 5
5
5 所以截面 的面积为 2 30 3 6 ,故④正确.
2 5 4
故选:B.
9.BC
【分析】根据导数的四则运算以及复合函数的导数,即可判断选项.
【详解】 ln 7 0,故 A错误;
x2 2 sin x 2xsin x x2 2 cos x,故 B正确;
x2 2x e x x2e x 2x x2
,故 C正确;ex
e 2x
ex
ln 3x 2
3
,故 D错误.3x 2
故选:BC
10.AB
【分析】AB选项,根据幂函数的性质得到 AB正确;C选项,不满足奇偶性;D选项,不
满足单调性.
【详解】A选项, y x3为奇函数且在 R上单调递增,满足要求,A正确;
1 1 1 1
B选项, g x x 3 的定义域为 R,且 g x x 3 x 3 g x ,故 g x x 3 为奇函数,
1 1
又 0,故
3 g x x
3 在 0, 单调递增,B正确;
C选项, y ex 为指数函数,结合图象可知其不是奇函数,C错误;
答案第 4页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
ln x,0 x 1
D选项, y ln x ,故当0 x 1时, y lnxln x, x 1 单调递减,D错误.
故选:AB
11.ABD
【分析】利用分类讨论及函数的单调性与导数的关系,结合函数的性质即可求解.
【详解】由题意可知,函数 f x 的定义域为 ,0 0, ,
m
当m 0时, f x 2x2 2 0,函数 f x 在 ,0 , 0, 上单调递增,故 B正确;x
当m 0时, f x x3, f x 2x 0,所以在 ,0 , 0, 上单调递增,故 D正确;
当m 0时,当 x 0时, f x x3 m 0 3 m;当 x 0时, f x x 0;
x x
故 A正确;C错误.
故选:ABD.
12.ABC
【分析】根据凸函数的定义,求导,即可根据二阶导数的正负判断.
【详解】对于 A,由 f x sinx cosx,得 f x =cosx-sinx,则
f x sinx cosx sinx cosx x (0, π=- + ,因为 ),所以
2
sin x 0,cos x 0, f x - sinx+cosx 0,所以此函数是凸函数;
对于 B,由 f x lnx 2x ,得 f x 1 2,则 f x 1 π2 ,因为 x (0, ),所以x x 2
f x 1 2 0,所以此函数是凸函数;x
C f x =-x3对于 ,由 2x 1,得 f x =-3x2 2,则 f x 6x,因为 x (0, π),所以
2
f x 6x 0,所以此函数是凸函数;
x x -x x x x x
对于 D,由 f x =-xe ,得 f x =-e xe ,则 f x e e -xe = 2 x e ,因为
x (0, π) f x 2 x e x,所以 0,所以此函数不是凸函数,
2
故选:ABC
13. 1 y (1 e)x
【分析】求出函数的导数,判断函数单调性,即可求得答案;根据导数的几何意义即可求得
答案第 5页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
曲线 y f (x)在 (1, f (1))处的切线方程.
【详解】由 f (x) x ex可得 f (x) 1 ex,
当 x 0时, f (x) 0,当 x 0时, f (x) 0,
故 f (x)在 ( , 0)上单调递增,在 (0, )上单调递减,
故 f (x)max f (0) 1;
由 f (1) 1 e,f (1) 1 e,
故曲线 y f (x)在 (1, f (1))处的切线方程为 y 1 e (1 e)(x 1),
即 y (1 e)x,
故答案为: 1; y (1 e)x
14.1
【分析】求出函数的导函数,令 f x 4x 3 2x 5,再利用导数说明函数的单调性,由
f 1 1,即可得到方程 4x3 2x 5 1的解,从而得解.
【详解】因为 y x 4 x 2 5x ,所以 y 4x3 2x 5,
f x 4x 3设函数 2x 5 2,则 f x 12x 2 0,
所以 f x 4x 3 2x 5在定义域R 上单调递增,
因为 f 1 1,所以方程 4x3 2x 5 1的解为 x 1,则所求切点的横坐标为1.
故答案为:1
15. ,6 2
3 1 2
【分析】函数 f x x ax 6x在区间 1,3 上单调递增,转化为 f x 0在 1,3 上恒成
2
立,即 a
6
3x 恒成立,利用基本不等式求最值可得答案.
x
1
【详解】因为 f x x3 ax2 6x,
2
所以 f x 3x2 ax 6,
3 1 2
因为函数 f x x ax 6x在区间 1,3 上单调递增,
2
所以 f x 3x2 ax 6 0在 1,3 上恒成立,
答案第 6页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
即 x 1,3 6时, a 3x 恒成立,
x
3x 6因为 2 3x 6 =6 2,当且仅当 x 2时等号成立,
x x
6
即 3x x
6 2,所以 a 6 2,
min
故答案为: ,6 2 .
16.[1, )
【分析】根据题意,构造函数 F(x) f (x) g(x)
1
,分 a 0与a 0 讨论,然后转化为F 0
a
恒成立,代入计算,即可得到结果.
【详解】构造函数 F(x) f (x) g(x),其定义域为 (0, ),
F (x) 1 (2x 1)(ax 1)则 2 2ax a , x (0, ),
x x
当a 0时, F (x) 0, f (x)单调递增,F 1 2 2a 0,F x 0不可能恒成立;
1 1
当a 0时,令 F (x) 0,得 x 或 x (舍去).
a 2
0 1当 x 时, F (x) 0;
a
x 1
1
当 时, F (x) 0,故 F (x)在 (0, )上有最大值 F ,
a a
F 1 0 1 1由题意知 恒成立,即 ln 1 0,
a a a
1 1
令 (a) ln 1,则 (a)在 (0, )上单调递减,且 (1) 0,
a a
1 1
故 ln 1 0成立的充要条件是 a 1.
a a
故答案为:[1, )
3π
17.(1)C
4
(2) 2
4
【分析】(1)根据余弦定理,即可求解;
(2)根据正弦定理以及二倍角公式,得到角和边的关系,再结合三角形的面积公式,即可
求解.
2
1 cosC a b
2 c2 2ab 2
【详解】( ) ,且C 0, π ,
2ab 2ab 2
答案第 7页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
所以C
3π
;
4
(2)根据正弦定理, c 2b cos B sinC 2sin B cos B sin 2B,
所以C 2B或C 2B π,
3π 3π
当C 2B时,C ,B ,此时B C π,不成立,
4 8
π
当C 2B π时,此时 A B ,则 a b 1,
8
ABC 1的面积 S ab sinC 1 1 1 2 2 .
2 2 2 4
18.(1)a 0.006,0.1
(2)0.3
【分析】(1)根据频率分布直方图的性质,求得 a 0.006,进而得到估计该校同学通关时
间低于钟的概率;
(2)根据题意得到通关时间位于区间 50,60 和 40,50 的人数,利用列举法求得基本事件
的总数,以及所求事件中包含的基本事件的个数,结合古典摡型的概率计算公式,即可求解.
【详解】(1)解:因为 0.004 a 0.018 0.022 2 0.028 10 1,所以 a 0.006,
由所给频率分布直方图可知,50名同学通关时间低于钟的频率为 0.004 0.006 10 0.1,
据此估计该校同学通关时间低于钟的概率为0.1 .
(2)解:样本中同学通关时间位于区间 50,60 的有50 0.006 10 3人,即为 A1, A2 , A3,
通关时间位于区间 40,50 的有:50 0.004 10 2(位),即为 B1, B2,
从这 5名入样同学中随机抽取 2人,所有可能的结果共有 10种,
分别为 A1, A2 , A1,A3 , A1,B1 , A1,B2 , A2 , A3 , A2 ,B1 , A2 ,B2 , A3 ,B1 , A3,B2 ,
B1,B2 ,
所抽取 2人的通关时间均位于区间 50,60 的结果有 3种,即 A1, A2 , A1,A3 , A2 , A3 ,
3
故此 2人的通关时间均位于区间 50,60 的概率为 P 0.3.
10
19.(1)an n
答案第 8页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
n
(2)
n 1
【分析】
S1,n 1
(1)根据 an S S ,n 2作差即可得解; n n 1
1 1
(2)由(1)可得bn ,利用裂项相消法计算可得.n n 1
【详解】(1) n
n(n 1)
数列的前 项和为 Sn ,2
1
n 1 a 1 1 当 时 1 S1 1,2
n
n 2 S n 1 当 时 n 1 ,2
n(n 1) n(n 1)
所以 an Sn Sn 1 n,2 2
又当 n 1时, an n也成立,
数列 an 的通项公式为 an n .
1 1 1 1
(2)由(1)可得bn a a ,n n 1 n n 1 n n 1
设数列 bn 的前 n项和为Tn,
则Tn b1 b2 b3 bn
1 1 1 1 1 1 1 1 1 1 n .
2 2 3 3 4 n n 1 n 1 n 1
2
20 x y
2
.(1) 1
12 4
(2) y x 2
【分析】(1)由长轴长和短轴长可得椭圆方程;
(2)联立直线方程与椭圆方程,利用韦达定理和弦长公式即可求得 m的值,则直线 AB的
方程可求.
【详解】(1)由已知长轴为 4 3,短轴长为 4,
可得 a 2 3,b 2,
答案第 9页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
2 2
则椭圆 C x y的标准方程为: 1;
12 4
y x m
(2)依题意 x2 y2 ,
1 12 4
解得 4x2 6mx 3m2 12 0,
因为 0,可得 4 m 4,
x1 x
3m
2
2
且 ,
x x 3m
2 12
1 2
4
2
因为 AB 1 k 2 x 9m1 x 2
2 4x1x
2
2 2 3m 124 3 2 ,
解得m 2,
所以直线 AB的方程为 l: y x 2.
21.(1) 114
3
(2)证明见解析
【分析】(1)依题建系,求得相关点和向量的坐标,利用点到直线的距离的空间向量计算公
式即可求得;
(2)由(1)中所建的系求出 A1C,DB,DE的坐标,分别计算得到 A1C DB 0和 A1C DE 0,
由线线垂直推出线面垂直.
【详解】(1)
如图,以D为原点,以DA,DC,DD1分别为 x, y, z轴正方向,建立空间直角坐标系,
正四棱柱 ABCD A1B1C1D1 , AA1 2AB 4,CC1 4CE,F 为 BD中点,
答案第 10页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
D1 0,0,4 ,E 0,2,1 ,F 1,1,0 ,ED1 0, 2,3 ,EF 1 , 1, 1
2
2
D 2EF d ED ED1 EF 13 1 114则点 1到直线 的距离为: 1 .
EF
3 3
(2)由(1)可得C 0,2,0 ,B 2,2,0 , A1 2,0,4 ,
则 A1C 2,2, 4 ,DB 2,2,0 ,DE 0,2,1 ,
由 A1C DB 2 2 2 2 0 可得 A1C DB,
又由 A1C DE 2 2 ( 4) 1 0可得 A1C DE,
又DB DE D,
故 A1C 面BDE .
22.(1)答案见解析
7
(2)a 2e
2
【分析】(1)对函数 f x 求导,分别讨论a 0和 a 0两种情况,即可求出结果;
x x
(2 1 2 2e)先分离参数,将原式化为 a x2 x ,构造函数 g x 1 x2 x 2 2e ,
2 x x 2 x x
利用导数判断 g x 的单调性进而求出 g x 的最大值即可.
【详解】(1) f x 的定义域为 0,+ , f x =a 2 ax 2 ,
x x
当a 0时, f (x) 0恒成立,所以 f x 的单调递减区间为 0,+ ,
当a 0时,令 f (x) 0
2 2
,则 x ,所以 f x 的单调递增区间为 , ,
a a
令 f (x) 0 0 x
2 2
,则
,所以 f x 的单调递减区间为 0, ,a a
综上:当 a 0时, f x 的单调递减区间为 0,+ ,无增区间;
当a 0时, f x 2 2 的单调递增区间为 , ,单调递减区间为 0, ;
a a
2 x 0 f x 1 x3 x2 2 2ex( )当 时, 2lnx恒成立,
2
即ax 2lnx
1
x3 x2 2 2ex 2lnx对 x 0恒成立,
2
答案第 11页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
a 1 x2 x 2 2e
x
即 对 x 0恒成立,
2 x x
g x 1 2 2e
x
令 x2 x ( x 0),
2 x x
g x x 1 2 2 x 1 e
x x3 x2 2 2 x 1 ex
x2 x2 x2
x 1 x2 2x 2 2 x 1 ex x 1 x2 2x 2 2ex
2 x x2
令m x x2 2x 2 2ex( x 0),则m (x) 2x 2 2ex,
令 t x m (x) 2x 2 2e x( x 0),则 t (x) 2 2ex,
由 x 0得, ex 1,所以 t (x) 0,所以 t x 在 0,+ 上单调递减,
所以 t x t 0 0,即m (x) 0,所以m x 在 0,+ 上单调递减,
所以m x m 0 0,
令 g (x) 0,则 0 x 1,所以 g x 在 0,1 单调递增,
令 g (x) 0,则 x 1,所以 g x 在 1, 单调递减,
所以 g x g 1 7 2e 7 ,所以 a 2e .
2 2
综上实数 a的取值范围为 a
7
2e .
2
1 2 2ex
【点睛】关键点点睛:本题第二问的关键是分离参数得 a x2 x 对 x 0恒成立,
2 x x
1 x
再设新函数 g x x2 x 2 2e ( x 0),对此求导研究其最值即可.
2 x x
答案第 12页,共 12页
{#{QQABbQAEogigAJBAABgCUQVACACQkBGACCoGgFAEoAAASAFABAA=}#}
同课章节目录
