2023年甘肃省武威市高中招生及毕业会考模拟数学模拟预测题(五)(含答案)
文档属性
| 名称 | 2023年甘肃省武威市高中招生及毕业会考模拟数学模拟预测题(五)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 22:59:16 | ||
图片预览




文档简介
武威市2023年高中招生及毕业会考模拟试题(五)
数学
(本试题满分120分,考试时间120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1. 下列各数中,是无理数的是( )
A. -2 B. 0 C. D.
2. 一个角的补角是130°,那么这个角的余角的大小是( )
A. 40° B. 50° C. 70° D. 140°
3. 已知为正整数,若一个在三角形的三边边长分别是,则满足条件的三角形中周长最短的为( )
A. 13 B. 16 C. 19 D. 22
4. 笃行实干谋新篇,陇原首季开门红,2023年一季度甘肃省地区生产总值达2670.7亿元.数据2670.7亿元用科学记数法可表示为( )
A. 元 B. 元 C. 元 D. 元
5. 2月8日,2024巴黎奥运会及残奥会项目图标正式公布.下面是部分项目的图标,其中是中心对称图形的是 ( )
A. B. C. D.
6. 某地积极践行生态绿色发展理念,空气质量状况大大改善.如图是该地在2023年4月空气质量等级统计图,则下列说法错误的是( )
A. 空气质量等级的众数为良
B. 污染程度为轻度及以上的天数占比20%
C. 空气质量优、良等级的比例达到三分之二
D. 若要制扇形统计图,轻微污染所占的扇形圆心角的度数为60°
7. 如图,边长相等的正五边形和正六边形拼接在一起,则的度数为( )
A. 22° B. 23° C. 24° D. 25°
8. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲乃发长安.问几何日相逢?大意是:甲从长安出发,用5日到达齐国;乙从齐国出发,用7日到达长安.乙从齐国先出发2日,甲才从长安出发.问甲出发几日,甲乙相逢?若设甲出发日,甲乙相逢,那么可列方程为( )
A. B. C. D.
9. 数学老师设置了一个数学版“羊了个羊”游戏.如图,一根6米长的绳子,一端拴在点处,另一端拴着一只小羊(把小羊近似看作点).已知墙体的左边是空地,,墙体长3米,小羊可以绕到草地上活动,请问小羊在草地上最大活动区域的周长是( )
A. 米 B. C. 米 D. 米
10. 如图1,点为矩形的边上一点,动点同时从点出发以相同的速度运动,其中点沿折线运动到点时停止,点沿运动到点时停止.设点出发时,的面积为,与的函数关系如图2所示(曲线为抛物线的一部分).现有下列结论:①;②的运动速度都是;③;④当时,.其中正确的结论有 ( )
A. ①③ B. ①④ C. ①②④ D. ②③④
二、填空题:本大题共8小题,每小题3分,共24分.
11. 计算:_____________.
12. 因式分解:___________.
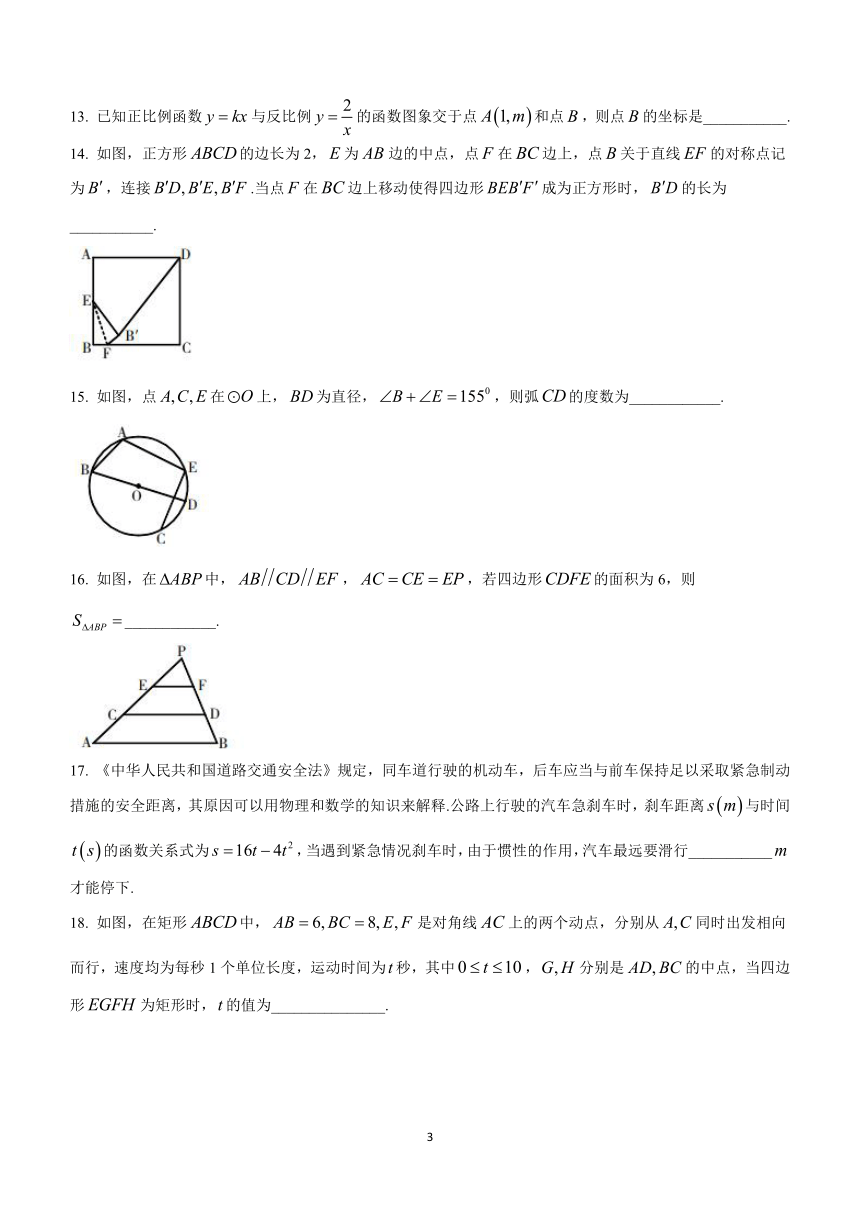
13. 已知正比例函数与反比例的函数图象交于点和点,则点的坐标是___________.
14. 如图,正方形的边长为2,为边的中点,点在边上,点关于直线的对称点记为,连接.当点在边上移动使得四边形成为正方形时,的长为___________.
15. 如图,点在上,为直径,,则弧的度数为____________.
16. 如图,在中,,,若四边形的面积为6,则____________.
17. 《中华人民共和国道路交通安全法》规定,同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距离,其原因可以用物理和数学的知识来解释.公路上行驶的汽车急刹车时,刹车距离与时间的函数关系式为,当遇到紧急情况刹车时,由于惯性的作用,汽车最远要滑行___________才能停下.
18. 如图,在矩形中,是对角线上的两个动点,分别从同时出发相向而行,速度均为每秒1个单位长度,运动时间为秒,其中,分别是的中点,当四边形为矩形时,的值为_______________.
三、解答题:本大题共5小题,共26分.解答时,应写出必要的文字说明,证明过程或演算步骤.
19.(4分)计算:
20.(4分)化简:
21.(6分)如图,两个村子在笔直河岸的同侧,两村到河岸的距离分别为,现在要在河岸上建一水厂向两村输送自来水,要求水厂到两村的距离之和最短.
(1)根据以上信息,在图中作出水厂的位置(要求:尺规作图,不写作法,保留作图痕迹);
(2)根据(1)完成的图,直接写出水厂到两村的距离之和的最小值为____________.
22.(6分)2022年我国建成基站超60万个,建设跑出“中国速度”.某地有一个信号塔,小敏想用所学的数学知识测量信号塔的高度,如图,在地平面上点处测得信号塔顶端的仰角为55°,从点向点方向前进2米到点,从点测得信号塔底端的仰角为37°,已知楼房的高度为21米.求信号塔的高度.
参考数据:,
23.(6分)在一个不透明的袋子中装有完全相同的四个小球,小球分别标有数字-2,-1,0,4.现从中任意摸出一个小球,将小球上面的数字记为;将小球放回袋中搅匀,再从中任意摸出一个小球,将小球上面的数字记为.
(1)从袋子中随机摸出一个小球,摸到的数字不是正数的概率为__________________;
(2)用列表或画树状图的方法表示出所有可能出现的结果,并求出点在第四象限的概率.
四、解答题:本大题共5小题,共40分.解答时,应写出必要的文字说明,证明过程或演算步骤.
24.(7分)运用语音识别输入软件可以提高文字输入的速度.为了解两种语音识别输入软件的准确性,小秦同学随机选取了20段话,其中每段话都含100个文字(不计标点符号).在保持相同语速的条件下,他用标准普通话朗读每段话来测试这两种语音识别输入软件的准确性.他的测试和分析过程如下:
【数据收集】
软件每次识别正确的字数:98,98,92,92,92,92,92,89,89,85,84,84,83,83,79,79,78,78,69,58
软件每次识别正确的字数:99,96,96,96,96,96,96,94,92,89,88,85,80,78,72,72,71,65,58,55
【数据整理】
根据上面得到的两组样本数据,绘制了频数分布直方图:
【数据分析】
平均数 84.7 83.7
众数 96
中位数 84.5
方差 88.91 184.01
请根据以上信息解答下列问题:
(1)填空:____________,___________;
(2)补全软件的频数分布直方图;
(3)根据以上信息,你认为哪种语音识别输入软件的准确性较好?说明你的理由(至少从两个不同的角度说明判断的合理性).
25.(7分)如图,为反比例函数图象上的一点,在轴正半轴有一点,,连接,且.
(1)求的值;
(2)过点作,交反比例函数的图象于点,连接交于点,求的值.
26. (8分)如图,已知是的直径,点是上异于的点,点是的中点,连接,过点作交的延长线于点,交的延长线于点,的平分线交于点,交于点.
(1)求证:是的切线;
(2)求的值.
27.(8分)如图,在矩形中,点是边上的一个动点(点与点不重合),连接,过点作,垂足为点,交或的延长线于点.
(1)若.
①当时,__________________;
②已知点是边的中点,当点在边上运动时,能不能经过点?若能,求出的长度;若不能,请说明理由;
(2)若.当点在边上运动时,求使得下列两个条件都成立的的取值范围:点始终在边上;点在某一位置时,点恰好与点重合.
28.(10分)已知抛物线(为常数,且)的对称轴为,且过点.点是抛物线上的一个动点,点的横坐标为,直线的解析式为,直线与轴相交于点,与轴相交于点.
(1)求抛物线的解析式;
(2)当直线与抛物线只有一个交点时,求点的坐标;
(3)当时,是否存在的值,使函数的最大值为?若存在,请求出的值;若不存在,请说明理由.
参考答案
一、 1----5 CACBA 6----10 DCADB
二、11. 4 12. 13. 14. 15. 50° 16. 18 17. 16
18. 2或8
三、19. 解:原式
20. 解:原式
21. 解:(1)如图所示,点即为水厂的位置:
(2)
22. 解:由题意得,在中,,米,
∴,∴(米)
∴(米)
在中,米,
∴,∴(米)
∵米,∴(米)
答:信号塔的高度为21.9米.
23.(1)
(2)解:画树状图为:
共有16种等可能的结果,其中点在第四象限的情况有2种,
∴点在第四象限的概率为.
四、24.(1)92 88.5
(2)补全频数分布直方图如图所示:
(3)我认为A种语音识别输入软件的准确性较好.
理由:A种语音识别输入软件的平均数较高,方差小,输入更稳定.
25. 解:(1)
如图,过点作轴,垂足为点,交于点.
∵,
∴,
∴,
∴点的坐标为.
∵为反比例函数图象上的一点,
∴;
(2)∵轴,,点在反比例函数的图象上,
∴,
∵,∴,
∴,
∵,∴.
∴.
26. 证明:(1)如图,连接.
∵,点是的中点,∴,,
∴,∴,
∴,∴,
∵,,
∴,
∵是的半径,∴是的切线.
(2)∵是直径,∴,
∵,,
∴,
∵,∴,
∵平分,
∴,,
∴,
∴.
27. 解:(1)①2;
②不能.
假设过点,则有,
∵,
∴,
又∵,
∴,∴,
设,
则有,整理得,
,该方程无解.
∴不能经过点.
(2)解:由(1)可知,,
设,则,
,
当时,有最大值,
当点始终在线段上时,,则有,
∴,又,∴,
当在某位置时,点恰好与点重合,
则均为直角三角形,
在中,有,
在中,有,
又∵,∴,
整理得:,
,
∴,
故的取值为12时,题中两个条件才成立.
28. 解:(1)由题意可得,该抛物线的对称轴为,
将点代入抛物线解析式得:,
联立,解得
∴抛物线的解析式为;
(2)由,消除整理得,
∵直线与抛物线只有一个交点,
∴,即,解得,
∴直线的解析式为,
令,得,
∴点的坐标为;
(3)分类讨论:
①当时,,∵,对称轴为,
∴此时随的增大而增大,∴的最大值,
由
解得或(舍去);
②当时,函数在顶点处取得最大值,
即当时,取得最大值(不符合题意,舍去);
③当时,,
∵,对称轴为,∴此时随的增大而减小,
∴当时,取得最大值,的最大值,
由,解得:(舍去)或
综上可知的值为或.
数学
(本试题满分120分,考试时间120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1. 下列各数中,是无理数的是( )
A. -2 B. 0 C. D.
2. 一个角的补角是130°,那么这个角的余角的大小是( )
A. 40° B. 50° C. 70° D. 140°
3. 已知为正整数,若一个在三角形的三边边长分别是,则满足条件的三角形中周长最短的为( )
A. 13 B. 16 C. 19 D. 22
4. 笃行实干谋新篇,陇原首季开门红,2023年一季度甘肃省地区生产总值达2670.7亿元.数据2670.7亿元用科学记数法可表示为( )
A. 元 B. 元 C. 元 D. 元
5. 2月8日,2024巴黎奥运会及残奥会项目图标正式公布.下面是部分项目的图标,其中是中心对称图形的是 ( )
A. B. C. D.
6. 某地积极践行生态绿色发展理念,空气质量状况大大改善.如图是该地在2023年4月空气质量等级统计图,则下列说法错误的是( )
A. 空气质量等级的众数为良
B. 污染程度为轻度及以上的天数占比20%
C. 空气质量优、良等级的比例达到三分之二
D. 若要制扇形统计图,轻微污染所占的扇形圆心角的度数为60°
7. 如图,边长相等的正五边形和正六边形拼接在一起,则的度数为( )
A. 22° B. 23° C. 24° D. 25°
8. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲乃发长安.问几何日相逢?大意是:甲从长安出发,用5日到达齐国;乙从齐国出发,用7日到达长安.乙从齐国先出发2日,甲才从长安出发.问甲出发几日,甲乙相逢?若设甲出发日,甲乙相逢,那么可列方程为( )
A. B. C. D.
9. 数学老师设置了一个数学版“羊了个羊”游戏.如图,一根6米长的绳子,一端拴在点处,另一端拴着一只小羊(把小羊近似看作点).已知墙体的左边是空地,,墙体长3米,小羊可以绕到草地上活动,请问小羊在草地上最大活动区域的周长是( )
A. 米 B. C. 米 D. 米
10. 如图1,点为矩形的边上一点,动点同时从点出发以相同的速度运动,其中点沿折线运动到点时停止,点沿运动到点时停止.设点出发时,的面积为,与的函数关系如图2所示(曲线为抛物线的一部分).现有下列结论:①;②的运动速度都是;③;④当时,.其中正确的结论有 ( )
A. ①③ B. ①④ C. ①②④ D. ②③④
二、填空题:本大题共8小题,每小题3分,共24分.
11. 计算:_____________.
12. 因式分解:___________.
13. 已知正比例函数与反比例的函数图象交于点和点,则点的坐标是___________.
14. 如图,正方形的边长为2,为边的中点,点在边上,点关于直线的对称点记为,连接.当点在边上移动使得四边形成为正方形时,的长为___________.
15. 如图,点在上,为直径,,则弧的度数为____________.
16. 如图,在中,,,若四边形的面积为6,则____________.
17. 《中华人民共和国道路交通安全法》规定,同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距离,其原因可以用物理和数学的知识来解释.公路上行驶的汽车急刹车时,刹车距离与时间的函数关系式为,当遇到紧急情况刹车时,由于惯性的作用,汽车最远要滑行___________才能停下.
18. 如图,在矩形中,是对角线上的两个动点,分别从同时出发相向而行,速度均为每秒1个单位长度,运动时间为秒,其中,分别是的中点,当四边形为矩形时,的值为_______________.
三、解答题:本大题共5小题,共26分.解答时,应写出必要的文字说明,证明过程或演算步骤.
19.(4分)计算:
20.(4分)化简:
21.(6分)如图,两个村子在笔直河岸的同侧,两村到河岸的距离分别为,现在要在河岸上建一水厂向两村输送自来水,要求水厂到两村的距离之和最短.
(1)根据以上信息,在图中作出水厂的位置(要求:尺规作图,不写作法,保留作图痕迹);
(2)根据(1)完成的图,直接写出水厂到两村的距离之和的最小值为____________.
22.(6分)2022年我国建成基站超60万个,建设跑出“中国速度”.某地有一个信号塔,小敏想用所学的数学知识测量信号塔的高度,如图,在地平面上点处测得信号塔顶端的仰角为55°,从点向点方向前进2米到点,从点测得信号塔底端的仰角为37°,已知楼房的高度为21米.求信号塔的高度.
参考数据:,
23.(6分)在一个不透明的袋子中装有完全相同的四个小球,小球分别标有数字-2,-1,0,4.现从中任意摸出一个小球,将小球上面的数字记为;将小球放回袋中搅匀,再从中任意摸出一个小球,将小球上面的数字记为.
(1)从袋子中随机摸出一个小球,摸到的数字不是正数的概率为__________________;
(2)用列表或画树状图的方法表示出所有可能出现的结果,并求出点在第四象限的概率.
四、解答题:本大题共5小题,共40分.解答时,应写出必要的文字说明,证明过程或演算步骤.
24.(7分)运用语音识别输入软件可以提高文字输入的速度.为了解两种语音识别输入软件的准确性,小秦同学随机选取了20段话,其中每段话都含100个文字(不计标点符号).在保持相同语速的条件下,他用标准普通话朗读每段话来测试这两种语音识别输入软件的准确性.他的测试和分析过程如下:
【数据收集】
软件每次识别正确的字数:98,98,92,92,92,92,92,89,89,85,84,84,83,83,79,79,78,78,69,58
软件每次识别正确的字数:99,96,96,96,96,96,96,94,92,89,88,85,80,78,72,72,71,65,58,55
【数据整理】
根据上面得到的两组样本数据,绘制了频数分布直方图:
【数据分析】
平均数 84.7 83.7
众数 96
中位数 84.5
方差 88.91 184.01
请根据以上信息解答下列问题:
(1)填空:____________,___________;
(2)补全软件的频数分布直方图;
(3)根据以上信息,你认为哪种语音识别输入软件的准确性较好?说明你的理由(至少从两个不同的角度说明判断的合理性).
25.(7分)如图,为反比例函数图象上的一点,在轴正半轴有一点,,连接,且.
(1)求的值;
(2)过点作,交反比例函数的图象于点,连接交于点,求的值.
26. (8分)如图,已知是的直径,点是上异于的点,点是的中点,连接,过点作交的延长线于点,交的延长线于点,的平分线交于点,交于点.
(1)求证:是的切线;
(2)求的值.
27.(8分)如图,在矩形中,点是边上的一个动点(点与点不重合),连接,过点作,垂足为点,交或的延长线于点.
(1)若.
①当时,__________________;
②已知点是边的中点,当点在边上运动时,能不能经过点?若能,求出的长度;若不能,请说明理由;
(2)若.当点在边上运动时,求使得下列两个条件都成立的的取值范围:点始终在边上;点在某一位置时,点恰好与点重合.
28.(10分)已知抛物线(为常数,且)的对称轴为,且过点.点是抛物线上的一个动点,点的横坐标为,直线的解析式为,直线与轴相交于点,与轴相交于点.
(1)求抛物线的解析式;
(2)当直线与抛物线只有一个交点时,求点的坐标;
(3)当时,是否存在的值,使函数的最大值为?若存在,请求出的值;若不存在,请说明理由.
参考答案
一、 1----5 CACBA 6----10 DCADB
二、11. 4 12. 13. 14. 15. 50° 16. 18 17. 16
18. 2或8
三、19. 解:原式
20. 解:原式
21. 解:(1)如图所示,点即为水厂的位置:
(2)
22. 解:由题意得,在中,,米,
∴,∴(米)
∴(米)
在中,米,
∴,∴(米)
∵米,∴(米)
答:信号塔的高度为21.9米.
23.(1)
(2)解:画树状图为:
共有16种等可能的结果,其中点在第四象限的情况有2种,
∴点在第四象限的概率为.
四、24.(1)92 88.5
(2)补全频数分布直方图如图所示:
(3)我认为A种语音识别输入软件的准确性较好.
理由:A种语音识别输入软件的平均数较高,方差小,输入更稳定.
25. 解:(1)
如图,过点作轴,垂足为点,交于点.
∵,
∴,
∴,
∴点的坐标为.
∵为反比例函数图象上的一点,
∴;
(2)∵轴,,点在反比例函数的图象上,
∴,
∵,∴,
∴,
∵,∴.
∴.
26. 证明:(1)如图,连接.
∵,点是的中点,∴,,
∴,∴,
∴,∴,
∵,,
∴,
∵是的半径,∴是的切线.
(2)∵是直径,∴,
∵,,
∴,
∵,∴,
∵平分,
∴,,
∴,
∴.
27. 解:(1)①2;
②不能.
假设过点,则有,
∵,
∴,
又∵,
∴,∴,
设,
则有,整理得,
,该方程无解.
∴不能经过点.
(2)解:由(1)可知,,
设,则,
,
当时,有最大值,
当点始终在线段上时,,则有,
∴,又,∴,
当在某位置时,点恰好与点重合,
则均为直角三角形,
在中,有,
在中,有,
又∵,∴,
整理得:,
,
∴,
故的取值为12时,题中两个条件才成立.
28. 解:(1)由题意可得,该抛物线的对称轴为,
将点代入抛物线解析式得:,
联立,解得
∴抛物线的解析式为;
(2)由,消除整理得,
∵直线与抛物线只有一个交点,
∴,即,解得,
∴直线的解析式为,
令,得,
∴点的坐标为;
(3)分类讨论:
①当时,,∵,对称轴为,
∴此时随的增大而增大,∴的最大值,
由
解得或(舍去);
②当时,函数在顶点处取得最大值,
即当时,取得最大值(不符合题意,舍去);
③当时,,
∵,对称轴为,∴此时随的增大而减小,
∴当时,取得最大值,的最大值,
由,解得:(舍去)或
综上可知的值为或.
同课章节目录
