2023年云南省昆明市第八中学初中学业水平考试九年级数学模拟预测题(四)(含答案)
文档属性
| 名称 | 2023年云南省昆明市第八中学初中学业水平考试九年级数学模拟预测题(四)(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 00:00:00 | ||
图片预览




文档简介
2023年云南省昆明市第八中学初中学业水平考试
数学模拟卷(四)
(全卷三个大题,共24个小题,共4页,满分100分,考试用时120分钟)
注意事项:
1.本卷为试题卷.考生必须在答题卡上解题作答.答案应书写在答题卡的相应位置上,在试题卷、草稿纸上作答无效.
2.考试结束后,请将试题卷和答题卡一并交回.
一、选择题(本大题共12小题,每小题只有一个正确选项,每小题3分,共36分)
1.据中国铁路昆明局集团有限公司消息,铁路“五一”小长假运输自2023年4月27日至5月4日,为期8天.云南铁路预计发送旅客2700000人次,超疫情前客流水平.其中数据2700000用科学记数法可表示为( )
A. B. C. D.
2.中国是最早采用正负数表示相反意义的量,并进行负数运算的国家.若水位上升3m记为+3m,那么水位下降1m应记为( )
A.+3m B. C.+1m D.
3.如图,,平分交于点,若,则的度数为( )
A.40° B.50° C.60° D.70°
4.如图是由几个完全相同的小正方体组成的立体图形,它的左视图是( )
A. B. C. D.
5.下列运算正确的是( )
A. B. C. D.
6.已知反比例函数的图象位于第一、三象限,则的取值范围是( )
A. B. C. D.
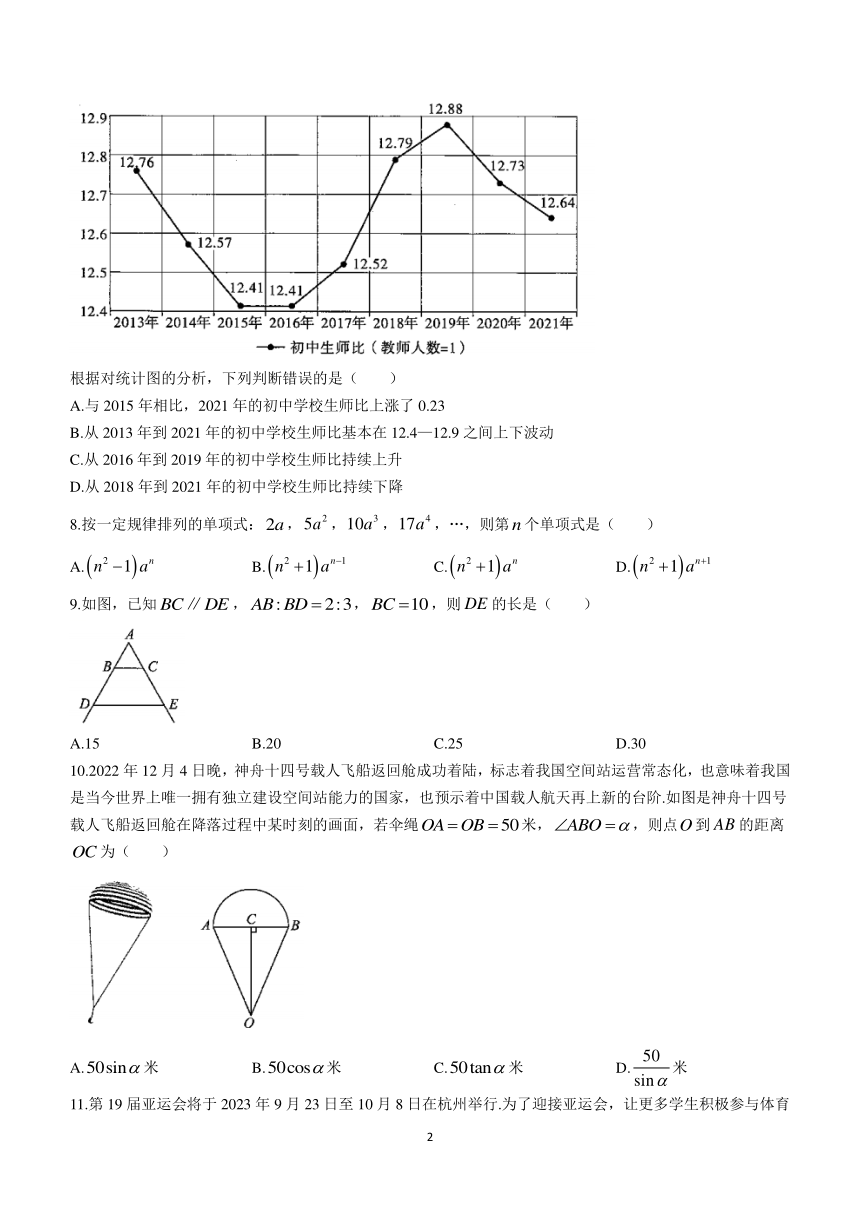
7.根据国家统计局统计数据显示,我国近几年(2013—2021年)的初中学校生师比如下图:
根据对统计图的分析,下列判断错误的是( )
A.与2015年相比,2021年的初中学校生师比上涨了0.23
B.从2013年到2021年的初中学校生师比基本在12.4—12.9之间上下波动
C.从2016年到2019年的初中学校生师比持续上升
D.从2018年到2021年的初中学校生师比持续下降
8.按一定规律排列的单项式:,,,,…,则第个单项式是( )
A. B. C. D.
9.如图,已知,,,则的长是( )
A.15 B.20 C.25 D.30
10.2022年12月4日晚,神舟十四号载人飞船返回舱成功着陆,标志着我国空间站运营常态化,也意味着我国是当今世界上唯一拥有独立建设空间站能力的国家,也预示着中国载人航天再上新的台阶.如图是神舟十四号载人飞船返回舱在降落过程中某时刻的画面,若伞绳米,,则点到的距离为( )
A.米 B.米 C.米 D.米
11.第19届亚运会将于2023年9月23日至10月8日在杭州举行.为了迎接亚运会,让更多学生积极参与体育运动,某校购买了一批篮球和足球,已知每个篮球比每个足球的进价多20元,且同样花费1600元,购进足球的数量比篮球多4个.设足球进价为每个元,则下列方程正确的是( )
A. B. C. D.
12.如图,在边长为6的正方形中,为上的点,为的中点,连接,,点,分别是和的中点,若,则的长为( )
A. B.2 C. D.3
二、填空题(本大题共4个小题,每小题2分,共8分)
13.若二次根式有意义,则实数的取值范围是__________.
14.若正多边形的每个内角的度数为140°,则这个正多边形的边数为___________.
15.分解因式:__________.
16.小吴同学在数学综合实践活动中,制作了一个圆锥模型(如图所示),经过小吴同学测量得到圆锥底面直径为10cm,圆锥的高为12cm,则根据测量数据推算该圆锥的侧面积为__________(结果保留).
三、解答题(本大题共8个小题,共56分)
17.(本小题满分6分)计算:.
18.(本小题满分6分)如图,点,,,在一条直线上,,,.求证:.
19.(本小题满分7分)2023年4月25日,云南省发展和改革委员会等六部门联合印发《云南省促进绿色消费实施方案》(下称《方案》),全面推动吃、穿、住、行、用、游等各领域消费绿色转型,统筹兼顾消费与生产、流通、回收、再利用各环节顺畅衔接,实现系统化节约减损和节能降耗.《方案》明确四项重点工作,即加快重点领域消费绿色转型、强化绿色消费科技和服务、健全绿色消费保障制度、完善绿色消费激励约束政策.为了促进《方案》有效实施,有关部门随机抽取了某个社区若干居民对《方案》进行满意度调查,将调查结果的满意度分为非常满意、满意、较满意、一般和不满意5种,每个居民只能从中选择一种,现将调查结果绘制成不完整的统计图表:
抽取的社区居民满意度的频数分布表
满意度 非常满意 满意 较满意 一般 不满意
频数 50 25 5
频率 0.50 0.25 0.05 0.05
根据以上信息,请回答下列问题:
(1)本次调查的样本容量是__________,__________,__________,__________;
(2)扇形统计图中,“不满意”对应的扇形的圆心角的度数为___________°;
(3)该社区有4000名居民,根据抽样调查的结果,请估计该社区居民对《方案》不满意的人数.
20.(本小题满分7分)2023年5月19日是第13个“中国旅游日”,将“美好中国,幸福旅程”2023年“5·19中国旅游日”主会场设在云南腾冲,是文化和旅游部贯彻落实党的二十大精神的重要举措,也是坚决落实2020年习近平总书记在腾冲考察时作出的“在全面建成小康社会基础上,大力推进乡村振兴,让幸福的地方更加幸福”重要指示的具体行动.5月19日上午在云南省保山市腾冲市和顺古镇举办主会场活动暨启动仪式,配套活动将于5月19日至21日集中开展,小昆和小明都应邀参加本次活动,他们了解到腾冲热海风景区、固东银杏村、火山地热国家地质公园、北海湿地都是腾冲旅游必去的打卡风景名胜景点,将腾冲热海风景区、固东银杏村、火山国家地质公园、北海湿地分别记为、、、.
(1)若小昆从这四个腾冲打卡风景名胜景点中,随机选择1个风景名胜景点旅游,则选中火山国家地质公园的概率为__________;
(2)小昆和小明都想要从腾冲热海风景区、固东银杏村、火山国家地质公园、北海湿地中任意选择1个景点旅游,用列表法或画树状图法中的一种方法,求他们选中不同景点的概率.
21.(本小题满分7分)如图,在四边形中,,,对角线的垂直平分线与边,分别相交于点,,与交于点,连接,.
(1)求证:四边形是菱形;
(2)若四边形的周长为40,,求的长.
22.(本小题满分7分)昆明某电商平台以每件20元的价格购进了一批商品进行销售,销售时该商品的售价不低于进价且不超过28元.经市场调查发现,该商品每天的销售量(件)与销售单价(元/件)之间满足如图所示的一次函数关系.
(1)求与之间的函数关系式;
(2)当销售单价为多少元时,销售利润最大?最大利润是多少元?
23.(本小题满分8分)如图,已知是的外接圆,是的直径,直线与相切于点,交弦于点,交优弧于点,连接,.
(1)求证:是的切线;
(2)若,,求的长.
24.(本小题满分8分)已知抛物线的顶点为点,过点的直线的解析式为.
(1)设是抛物线与直线交点的横坐标,求证:;
(2)抛物线与轴从左至右交于,两点,分别过点和点作轴的垂线,交直线于点和点,将抛物线沿其对称轴平移,使平移后的抛物线与线段总有公共点.试探究:拋物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
2023年云南省昆明市第八中学初中学业水平考试
九年级数学(四)
参考答案
1.B 【解析】科学记数法的表示形式为,其中,为整数.数据.故选B.
2.D 【解析】水位上升3m记为+3m,那么水位下降1m应记为.故选D.
3.B 【解析】∵,∴.
∵平分,,∴,
∴.故选B.
4.A 【解析】观察该几何体可得三视图如下:
故选A.
5.A 【解析】A.,选项正确,故A选项符合题意;
B.,选项错误,故B选项不符合题意;
C.,选项错误,故C选项不符合题意;
D.,选项错误,故D选项不符合题意.
故选A.
6.B 【解析】∵反比例函数的图象位于第一、三象限,
∴,∴.故选B.
7.D 【解析】由折线统计图可知,
A.与2015年相比,2021年的初中学校生师比上涨了0.23,说法正确,故A选项不符合题意;
B.从2013年到2021年的初中学校生师比基本在12.4—12.9之间上下波动,说法正确,故B选项不符合题意;
C.从2016年到2019年的初中学校生师比持续上升,说法正确,故C选项不符合题意;
D.从2018年到2021年的初中学校生师比持续下降,说法错误,故D选项符合题意.
故选D.
8.C 【解析】观察规律可知第个单项式为:.故选C.
9.C 【解析】∵,∴,∴,
∵,∴.
∵,∴,∴.
故选C.
10.A 【解析】∵米,,
在中,∴,
∴(米).
故选A.
11.B 【解析】设足球进价为每个元,则篮球进价为每个元,根据题意可列出方程为.故选B.
12.C 【解析】∵,,∴.
∵为的中点,∴.
在中,,由勾股定理可得,
,
∵点,分别是和的中点,
∴是的中位线,∴.
故选C.
13. 【解析】∵二次根式有意义,
∴,解得:.故答案为.
14.9 【解析】∵正多边形的每个内角都是140°,
∴该正多边形的每个外角的度数:,
∴该正多边形的边数为.
故答案为9.
15. 【解析】.
故答案为.
16. 【解析】∵,(cm),
可设圆锥母线长为,
由勾股定理,(cm),
圆锥侧面展开图的面积为:,
所以圆锥的侧面积为.
故答案为.
17.解:原式.
18.证明:∵,∴,∴.
在和中,,
∴.
19.解:(1)样本容量为,,,,
所以填100、15、0.15、5.
(2),所以填18.
(3)∵估计该社区居民中对《方案》不满意的人数大约占全社区居民的5%,
∴(名).
答:根据样本估计总体的思想,该社区对《方案》不满意的居民人数大约有200名.
20.解:(1)小昆从四个腾冲打卡风景名胜景点中,随机选择1个风景名胜景点旅游,共有4种等可能情况,恰好选中火山国家地质公园的情况只有1种,故选中火山国家地质公园的概率为.
(2)列表如下:
小明小昆
或画树状图如下:
∵共有16种等可能的结果,其中小昆和小明选中不同景点有12种情况,分别是、、、、、、、、、、、,
∴小昆和小明选中不同景点的概率:,即(选中不同景点).
21.(1)证明:,
∴.
∵直线是对角线的垂直平分线,
∴,.
在和中,,
∴,∴.
∵,∴四边形是平行四边形.
∵,∴四边形是菱形.
(2)解:∵菱形的周长为40,
∴,
又∵,∴.
在中,由勾股定理得,
∴.
∵,
∴,∴.
22.解:(1)设与之间的函数关系式为,
由题意可得,解得,
∴与之间的函数关系式为.
(2)设利润为元,得:,
∵,∴抛物线开口向下,
当时,的值随的增大而增大.
∵,∴当时,元.
答:当销售单价为28元时,销售利润最大,最大利润为1120元.
23.(1)证明:∵与相切,∴.
∵,∴.
∵,∴,,∴.
在和中,,
∴.
∴,∴.
∵是的半径,,∴是的切线.
(2)解:∵,∴.
∵是的直径,∴.
∵,∴.
∵,,
∴在中,设,则.
∵,,
∴是的中位线,∴,
∴,
在中,由勾股定理可得,
,解得:,(舍),
∴,.
∵,,
∴,∴,∴.
故的长为.
24.解:(1)法一:,
所以顶点的坐标为,
将点的坐标代入直线的解析式得,,解得,
所以直线的解析式为.
因为是抛物线与直线交点的横坐标,所以,
化简得,解得,,
当时,;
当时,.
综上所述,.
法二:,
所以顶点的坐标为,
将点的坐标代入直线的解析式得,,解得,
所以直线的解析式为.
因为是抛物线与直线交点的横坐标,所以,
化简得,即,
所以,
由可知,,所以.
(2)如图,在二次函数中,令得,
,解得,,
所以,.
在一次函数中,令,得;令,得.
所以,.
①当抛物线向上平移,可设解析式为,
联立方程组可得:,
化简得,所以,
所以,所以;
②当抛物线向下平移,可设解析式为,
当时,,当时,,
所以,或,所以或,所以.
综上所述,抛物线向上最多可平移个单位长度,向下最多可平移6个单位长度.
数学模拟卷(四)
(全卷三个大题,共24个小题,共4页,满分100分,考试用时120分钟)
注意事项:
1.本卷为试题卷.考生必须在答题卡上解题作答.答案应书写在答题卡的相应位置上,在试题卷、草稿纸上作答无效.
2.考试结束后,请将试题卷和答题卡一并交回.
一、选择题(本大题共12小题,每小题只有一个正确选项,每小题3分,共36分)
1.据中国铁路昆明局集团有限公司消息,铁路“五一”小长假运输自2023年4月27日至5月4日,为期8天.云南铁路预计发送旅客2700000人次,超疫情前客流水平.其中数据2700000用科学记数法可表示为( )
A. B. C. D.
2.中国是最早采用正负数表示相反意义的量,并进行负数运算的国家.若水位上升3m记为+3m,那么水位下降1m应记为( )
A.+3m B. C.+1m D.
3.如图,,平分交于点,若,则的度数为( )
A.40° B.50° C.60° D.70°
4.如图是由几个完全相同的小正方体组成的立体图形,它的左视图是( )
A. B. C. D.
5.下列运算正确的是( )
A. B. C. D.
6.已知反比例函数的图象位于第一、三象限,则的取值范围是( )
A. B. C. D.
7.根据国家统计局统计数据显示,我国近几年(2013—2021年)的初中学校生师比如下图:
根据对统计图的分析,下列判断错误的是( )
A.与2015年相比,2021年的初中学校生师比上涨了0.23
B.从2013年到2021年的初中学校生师比基本在12.4—12.9之间上下波动
C.从2016年到2019年的初中学校生师比持续上升
D.从2018年到2021年的初中学校生师比持续下降
8.按一定规律排列的单项式:,,,,…,则第个单项式是( )
A. B. C. D.
9.如图,已知,,,则的长是( )
A.15 B.20 C.25 D.30
10.2022年12月4日晚,神舟十四号载人飞船返回舱成功着陆,标志着我国空间站运营常态化,也意味着我国是当今世界上唯一拥有独立建设空间站能力的国家,也预示着中国载人航天再上新的台阶.如图是神舟十四号载人飞船返回舱在降落过程中某时刻的画面,若伞绳米,,则点到的距离为( )
A.米 B.米 C.米 D.米
11.第19届亚运会将于2023年9月23日至10月8日在杭州举行.为了迎接亚运会,让更多学生积极参与体育运动,某校购买了一批篮球和足球,已知每个篮球比每个足球的进价多20元,且同样花费1600元,购进足球的数量比篮球多4个.设足球进价为每个元,则下列方程正确的是( )
A. B. C. D.
12.如图,在边长为6的正方形中,为上的点,为的中点,连接,,点,分别是和的中点,若,则的长为( )
A. B.2 C. D.3
二、填空题(本大题共4个小题,每小题2分,共8分)
13.若二次根式有意义,则实数的取值范围是__________.
14.若正多边形的每个内角的度数为140°,则这个正多边形的边数为___________.
15.分解因式:__________.
16.小吴同学在数学综合实践活动中,制作了一个圆锥模型(如图所示),经过小吴同学测量得到圆锥底面直径为10cm,圆锥的高为12cm,则根据测量数据推算该圆锥的侧面积为__________(结果保留).
三、解答题(本大题共8个小题,共56分)
17.(本小题满分6分)计算:.
18.(本小题满分6分)如图,点,,,在一条直线上,,,.求证:.
19.(本小题满分7分)2023年4月25日,云南省发展和改革委员会等六部门联合印发《云南省促进绿色消费实施方案》(下称《方案》),全面推动吃、穿、住、行、用、游等各领域消费绿色转型,统筹兼顾消费与生产、流通、回收、再利用各环节顺畅衔接,实现系统化节约减损和节能降耗.《方案》明确四项重点工作,即加快重点领域消费绿色转型、强化绿色消费科技和服务、健全绿色消费保障制度、完善绿色消费激励约束政策.为了促进《方案》有效实施,有关部门随机抽取了某个社区若干居民对《方案》进行满意度调查,将调查结果的满意度分为非常满意、满意、较满意、一般和不满意5种,每个居民只能从中选择一种,现将调查结果绘制成不完整的统计图表:
抽取的社区居民满意度的频数分布表
满意度 非常满意 满意 较满意 一般 不满意
频数 50 25 5
频率 0.50 0.25 0.05 0.05
根据以上信息,请回答下列问题:
(1)本次调查的样本容量是__________,__________,__________,__________;
(2)扇形统计图中,“不满意”对应的扇形的圆心角的度数为___________°;
(3)该社区有4000名居民,根据抽样调查的结果,请估计该社区居民对《方案》不满意的人数.
20.(本小题满分7分)2023年5月19日是第13个“中国旅游日”,将“美好中国,幸福旅程”2023年“5·19中国旅游日”主会场设在云南腾冲,是文化和旅游部贯彻落实党的二十大精神的重要举措,也是坚决落实2020年习近平总书记在腾冲考察时作出的“在全面建成小康社会基础上,大力推进乡村振兴,让幸福的地方更加幸福”重要指示的具体行动.5月19日上午在云南省保山市腾冲市和顺古镇举办主会场活动暨启动仪式,配套活动将于5月19日至21日集中开展,小昆和小明都应邀参加本次活动,他们了解到腾冲热海风景区、固东银杏村、火山地热国家地质公园、北海湿地都是腾冲旅游必去的打卡风景名胜景点,将腾冲热海风景区、固东银杏村、火山国家地质公园、北海湿地分别记为、、、.
(1)若小昆从这四个腾冲打卡风景名胜景点中,随机选择1个风景名胜景点旅游,则选中火山国家地质公园的概率为__________;
(2)小昆和小明都想要从腾冲热海风景区、固东银杏村、火山国家地质公园、北海湿地中任意选择1个景点旅游,用列表法或画树状图法中的一种方法,求他们选中不同景点的概率.
21.(本小题满分7分)如图,在四边形中,,,对角线的垂直平分线与边,分别相交于点,,与交于点,连接,.
(1)求证:四边形是菱形;
(2)若四边形的周长为40,,求的长.
22.(本小题满分7分)昆明某电商平台以每件20元的价格购进了一批商品进行销售,销售时该商品的售价不低于进价且不超过28元.经市场调查发现,该商品每天的销售量(件)与销售单价(元/件)之间满足如图所示的一次函数关系.
(1)求与之间的函数关系式;
(2)当销售单价为多少元时,销售利润最大?最大利润是多少元?
23.(本小题满分8分)如图,已知是的外接圆,是的直径,直线与相切于点,交弦于点,交优弧于点,连接,.
(1)求证:是的切线;
(2)若,,求的长.
24.(本小题满分8分)已知抛物线的顶点为点,过点的直线的解析式为.
(1)设是抛物线与直线交点的横坐标,求证:;
(2)抛物线与轴从左至右交于,两点,分别过点和点作轴的垂线,交直线于点和点,将抛物线沿其对称轴平移,使平移后的抛物线与线段总有公共点.试探究:拋物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
2023年云南省昆明市第八中学初中学业水平考试
九年级数学(四)
参考答案
1.B 【解析】科学记数法的表示形式为,其中,为整数.数据.故选B.
2.D 【解析】水位上升3m记为+3m,那么水位下降1m应记为.故选D.
3.B 【解析】∵,∴.
∵平分,,∴,
∴.故选B.
4.A 【解析】观察该几何体可得三视图如下:
故选A.
5.A 【解析】A.,选项正确,故A选项符合题意;
B.,选项错误,故B选项不符合题意;
C.,选项错误,故C选项不符合题意;
D.,选项错误,故D选项不符合题意.
故选A.
6.B 【解析】∵反比例函数的图象位于第一、三象限,
∴,∴.故选B.
7.D 【解析】由折线统计图可知,
A.与2015年相比,2021年的初中学校生师比上涨了0.23,说法正确,故A选项不符合题意;
B.从2013年到2021年的初中学校生师比基本在12.4—12.9之间上下波动,说法正确,故B选项不符合题意;
C.从2016年到2019年的初中学校生师比持续上升,说法正确,故C选项不符合题意;
D.从2018年到2021年的初中学校生师比持续下降,说法错误,故D选项符合题意.
故选D.
8.C 【解析】观察规律可知第个单项式为:.故选C.
9.C 【解析】∵,∴,∴,
∵,∴.
∵,∴,∴.
故选C.
10.A 【解析】∵米,,
在中,∴,
∴(米).
故选A.
11.B 【解析】设足球进价为每个元,则篮球进价为每个元,根据题意可列出方程为.故选B.
12.C 【解析】∵,,∴.
∵为的中点,∴.
在中,,由勾股定理可得,
,
∵点,分别是和的中点,
∴是的中位线,∴.
故选C.
13. 【解析】∵二次根式有意义,
∴,解得:.故答案为.
14.9 【解析】∵正多边形的每个内角都是140°,
∴该正多边形的每个外角的度数:,
∴该正多边形的边数为.
故答案为9.
15. 【解析】.
故答案为.
16. 【解析】∵,(cm),
可设圆锥母线长为,
由勾股定理,(cm),
圆锥侧面展开图的面积为:,
所以圆锥的侧面积为.
故答案为.
17.解:原式.
18.证明:∵,∴,∴.
在和中,,
∴.
19.解:(1)样本容量为,,,,
所以填100、15、0.15、5.
(2),所以填18.
(3)∵估计该社区居民中对《方案》不满意的人数大约占全社区居民的5%,
∴(名).
答:根据样本估计总体的思想,该社区对《方案》不满意的居民人数大约有200名.
20.解:(1)小昆从四个腾冲打卡风景名胜景点中,随机选择1个风景名胜景点旅游,共有4种等可能情况,恰好选中火山国家地质公园的情况只有1种,故选中火山国家地质公园的概率为.
(2)列表如下:
小明小昆
或画树状图如下:
∵共有16种等可能的结果,其中小昆和小明选中不同景点有12种情况,分别是、、、、、、、、、、、,
∴小昆和小明选中不同景点的概率:,即(选中不同景点).
21.(1)证明:,
∴.
∵直线是对角线的垂直平分线,
∴,.
在和中,,
∴,∴.
∵,∴四边形是平行四边形.
∵,∴四边形是菱形.
(2)解:∵菱形的周长为40,
∴,
又∵,∴.
在中,由勾股定理得,
∴.
∵,
∴,∴.
22.解:(1)设与之间的函数关系式为,
由题意可得,解得,
∴与之间的函数关系式为.
(2)设利润为元,得:,
∵,∴抛物线开口向下,
当时,的值随的增大而增大.
∵,∴当时,元.
答:当销售单价为28元时,销售利润最大,最大利润为1120元.
23.(1)证明:∵与相切,∴.
∵,∴.
∵,∴,,∴.
在和中,,
∴.
∴,∴.
∵是的半径,,∴是的切线.
(2)解:∵,∴.
∵是的直径,∴.
∵,∴.
∵,,
∴在中,设,则.
∵,,
∴是的中位线,∴,
∴,
在中,由勾股定理可得,
,解得:,(舍),
∴,.
∵,,
∴,∴,∴.
故的长为.
24.解:(1)法一:,
所以顶点的坐标为,
将点的坐标代入直线的解析式得,,解得,
所以直线的解析式为.
因为是抛物线与直线交点的横坐标,所以,
化简得,解得,,
当时,;
当时,.
综上所述,.
法二:,
所以顶点的坐标为,
将点的坐标代入直线的解析式得,,解得,
所以直线的解析式为.
因为是抛物线与直线交点的横坐标,所以,
化简得,即,
所以,
由可知,,所以.
(2)如图,在二次函数中,令得,
,解得,,
所以,.
在一次函数中,令,得;令,得.
所以,.
①当抛物线向上平移,可设解析式为,
联立方程组可得:,
化简得,所以,
所以,所以;
②当抛物线向下平移,可设解析式为,
当时,,当时,,
所以,或,所以或,所以.
综上所述,抛物线向上最多可平移个单位长度,向下最多可平移6个单位长度.
同课章节目录
