6.3.1 实数的概念 课件(共21张PPT)
文档属性
| 名称 | 6.3.1 实数的概念 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 838.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 06:58:43 | ||
图片预览








文档简介
(共21张PPT)
6.3.1 实数的概念
人教版数学·七年级下册
1.还记得什么是有理数吗?你能举出一些例子吗?
复习导入
2.有理数是怎么分类的呢?
整数和分数统称为有理数.
3.请把下列各数填写在对应的集合内:
复习导入
整数集合:{ }
分数集合:{ }
有理数数集合:{ }
探究新知
1.请把下列有理数化为小数的形式.
发现:它们可以分为有限小数和无限循环小数两类.
探究新知
归纳:任何一个有理数都可以写成__________小数或
___________________小数的形式.
反过来任何有限小数或无限循环小数也都是有理数.
有限小数
无限循环小数
探究新知
2.请用计算器把下列各数写成小数的形式.
思考:观察得出来的结果,你有什么发现?
探究新知
结论:它们是_______________小数.
我们把无限不循环小数叫做无理数.
常见的三种无理数:
(1)化简后含有 π 的数;
(2)开方开不尽的数;
(3)有规律但不循环的小数,如 1.01001000100001…
认识无理数后,我们把有理数和无理数统称为实数.
无限不循环
针对练习
把下列各数分别填入相应的集合内:
0.101,
有理数集合
无理数集合
...
...
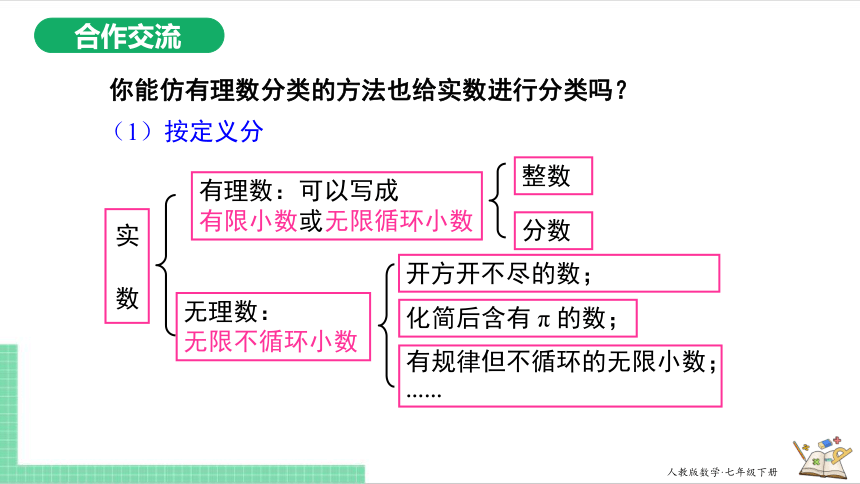
合作交流
你能仿有理数分类的方法也给实数进行分类吗?
无理数:
无限不循环小数
有理数:可以写成
有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
开方开不尽的数;
有规律但不循环的无限小数;
……
化简后含有 π 的数;
合作交流
你能仿有理数分类的方法也给实数进行分类吗?
负实数
正实数
数实
正有理数
负有理数
(2)按符号分
0
正无理数
负无理数
例1 把下列各数分别填入相应的括号内:
例题讲解
无理数:
有理数:
负实数:
正实数:
实数与数轴
我们知道有理数可以用数轴上的点表示,那么无理数能否用数轴上的点来表示呢?
请思考: 能不能表示在数轴上呢?
-2
-1
0
1
2
实数与数轴
我们知道直径是1的圆的周长为 π,那么将圆在数轴上从原点往右
滚动一周得到点 A ,则A表示的数是无理数 π.
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
A
用两个面积为1的小正方形可以拼成一个面积为 2 的大正方形。这时大正方形的边长就是 ,即小正方形的对角线是 .
实数与数轴
-1
-2
0
2
1
3
实数与数轴
归纳:
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数.
实数
数轴上的点
一一对应
针对练习
请将图中数轴上标有字母的各点与下列实数对应起来:
课堂小结
1:举例说明有理数和无理数的特点是什么?
2:实数是由哪些数组成的?
3:实数与数轴上的点有什么关系?
课堂练习
1.下列各数为无理数的是( )
A. 0.618 B. C. D.
2.下列说法:①带根号的数是无理数;②不含根号的数一定是有理数;③无理数是开方开不尽的数;④无限不循环小数是无理数;⑤π是无理数.
其中正确的有( C )
A. 4个 B. 3个 C. 2个 D. 1个
C
C
课堂练习
3.写出一个在1到3之间的无理数: .
4.下列说法中,正确的是( C )
A.无理数包括正无理数、零和负无理数
B.无限小数都是无理数
C.正实数包括正有理数和正无理数
D.实数可以分为正实数和负实数两类
C
(答案不唯一)
课堂练习
5.有一个数值转换器,原理如下.当输入的x为4时,输出的y是( C )
A. 4 B. 2 C. D.
C
课堂练习
6.如图,已知直径为1个单位长度的圆形纸片上的点A与数轴上表示-1的点重合,若将该圆形纸片沿数轴滚动一周(无滑动)后点A与数轴上的点A'重合,则点A'表示的数为___________________.
π-1或-π-1
6.3.1 实数的概念
人教版数学·七年级下册
1.还记得什么是有理数吗?你能举出一些例子吗?
复习导入
2.有理数是怎么分类的呢?
整数和分数统称为有理数.
3.请把下列各数填写在对应的集合内:
复习导入
整数集合:{ }
分数集合:{ }
有理数数集合:{ }
探究新知
1.请把下列有理数化为小数的形式.
发现:它们可以分为有限小数和无限循环小数两类.
探究新知
归纳:任何一个有理数都可以写成__________小数或
___________________小数的形式.
反过来任何有限小数或无限循环小数也都是有理数.
有限小数
无限循环小数
探究新知
2.请用计算器把下列各数写成小数的形式.
思考:观察得出来的结果,你有什么发现?
探究新知
结论:它们是_______________小数.
我们把无限不循环小数叫做无理数.
常见的三种无理数:
(1)化简后含有 π 的数;
(2)开方开不尽的数;
(3)有规律但不循环的小数,如 1.01001000100001…
认识无理数后,我们把有理数和无理数统称为实数.
无限不循环
针对练习
把下列各数分别填入相应的集合内:
0.101,
有理数集合
无理数集合
...
...
合作交流
你能仿有理数分类的方法也给实数进行分类吗?
无理数:
无限不循环小数
有理数:可以写成
有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
开方开不尽的数;
有规律但不循环的无限小数;
……
化简后含有 π 的数;
合作交流
你能仿有理数分类的方法也给实数进行分类吗?
负实数
正实数
数实
正有理数
负有理数
(2)按符号分
0
正无理数
负无理数
例1 把下列各数分别填入相应的括号内:
例题讲解
无理数:
有理数:
负实数:
正实数:
实数与数轴
我们知道有理数可以用数轴上的点表示,那么无理数能否用数轴上的点来表示呢?
请思考: 能不能表示在数轴上呢?
-2
-1
0
1
2
实数与数轴
我们知道直径是1的圆的周长为 π,那么将圆在数轴上从原点往右
滚动一周得到点 A ,则A表示的数是无理数 π.
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
A
用两个面积为1的小正方形可以拼成一个面积为 2 的大正方形。这时大正方形的边长就是 ,即小正方形的对角线是 .
实数与数轴
-1
-2
0
2
1
3
实数与数轴
归纳:
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数.
实数
数轴上的点
一一对应
针对练习
请将图中数轴上标有字母的各点与下列实数对应起来:
课堂小结
1:举例说明有理数和无理数的特点是什么?
2:实数是由哪些数组成的?
3:实数与数轴上的点有什么关系?
课堂练习
1.下列各数为无理数的是( )
A. 0.618 B. C. D.
2.下列说法:①带根号的数是无理数;②不含根号的数一定是有理数;③无理数是开方开不尽的数;④无限不循环小数是无理数;⑤π是无理数.
其中正确的有( C )
A. 4个 B. 3个 C. 2个 D. 1个
C
C
课堂练习
3.写出一个在1到3之间的无理数: .
4.下列说法中,正确的是( C )
A.无理数包括正无理数、零和负无理数
B.无限小数都是无理数
C.正实数包括正有理数和正无理数
D.实数可以分为正实数和负实数两类
C
(答案不唯一)
课堂练习
5.有一个数值转换器,原理如下.当输入的x为4时,输出的y是( C )
A. 4 B. 2 C. D.
C
课堂练习
6.如图,已知直径为1个单位长度的圆形纸片上的点A与数轴上表示-1的点重合,若将该圆形纸片沿数轴滚动一周(无滑动)后点A与数轴上的点A'重合,则点A'表示的数为___________________.
π-1或-π-1
