2023年浙江省宁波市中考数学模拟预测题(三)(含答案)
文档属性
| 名称 | 2023年浙江省宁波市中考数学模拟预测题(三)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 07:09:00 | ||
图片预览



文档简介
宁波市2023年中考全景复习指导(三)
数学试题
一、选择题(每小题4分,共40分.在每小题给出的四个选项中,只有一项符合题目要求)
1.下列各数中,的相反数的倒数是( )
A.4 B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.我国神舟十三号载人飞船和航天员乘组于2022年4月16日返回地球,结束了183天的在轨飞行从2003年神舟五号载人飞船上天以来,我国已有13位航天员出征太空,绕地球飞行共约2.32亿公里.将数据232000000用科学记数法表示为( )
A. B. C. D.
4.如图所示,几何体的左视图是( )
A. B. C. D.
5.下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩(单位:)的平均数和方差.要从中选择一名成绩较高且发挥稳定的运动员参加决赛,最合适的运动员是( )
甲 乙 丙 丁
平均数 350 376 350 376
方差 13.5 2.4 5.4 12.5
A.甲 B.乙 C.丙 D.丁
6.圆锥的侧面积为,母线长为4,则它的底面半径为( )
A.2 B.1 C.3 D.4
7.如图.中,,点是的重心,连结并延长交于点,连结并延长交于点,连结.若,,则的长为( )
A.5 B.4 C.3 D.2
8.《九章算术》是中国古代重要的数学著作,其中有这样一道题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗,问醇、行酒各得几何?”译文:今有醇酒(优质酒)1斗,价格50钱;行酒(勾兑酒)1斗,价格10钱.现有30钱,买2斗酒,问能买醇酒、行酒各多少斗?设能买醇酒斗,行酒斗,可列二元一次方程组为( )
A. B. C. D.
9.在平面直角坐标系中,将二次函数的图象平移,使平移后的图象经过原点.设平移后的图象对应的函数表达式为,当时,随的增大而减小,则的取值范围为( )
A. B. C. D.
10.如图,以为直径的半圆与矩形的边相切于点,边与半圆交于点.要求矩形的面积,只需要知道下列哪两个点之间的距离( )
A.点与点 B.点与点 C.点与点 D.点与点
二、填空题(每小题5分,共30分)
11.请写出一个大于且小于1的无理数:______.
12.分解因式:______.
13.一个不透明的袋子中装有3个红球和2个白球,这些球除颜色不同外,其余均相同,从中任意摸出一个球,这个球是白球的概率为______.
14.定义一种新运算:对于任意的非零实数,,.若,则的值为______.
15.如图,中,,,,,点是线段上一动点,当半径为6的与的一边相切时,的长为______.
16.如图,的顶点,分别落在反比例函数和的图象上,连结,将沿着翻折,点的对应点恰好落在的图象上,与交于点.已知的面积为,,则的值为______,的值为______.
三、解答题(本大题有8小题,17~19题每题8分,20~22题每题10分,23题12分,24题14分,共80分)
17.(1)计算:.
(2)解不等式组
18.图1、图2是的网格,网格中每个小正方形的边长均为1,请按要求画出下列图形,所画图形的各个顶点均在小正方形的顶点上.
图1 图2
(1)在图1中画出以为一边的成中心对称的四边形,使其面积为12;
(2)在图2中画出一个以为一边的,使其是面积为的轴对称图形.
19.用水问题一直是人民关注的热点问题,为此,小明随机抽取自己家中一年5个月的月用水量(单位:吨),并对每个月的月平均气温(单位:℃)进行了统计,得到下列统计图
(1)小明家这5个月的月平均用水量为______吨;
(2)下列推断:①当地当年月平均气温的众数是;
②当地当年月平均气温的中位数为;
③小明家这5个月的月用水量随着月平均气温的变化而变化,温度越高,月用水量越大.所有合理推断的序号是______;
(3)如果用小明家5月、7月、9月这三个月的月平均用水量估计当年的用水总量,你认为是否合理?并说明理由.
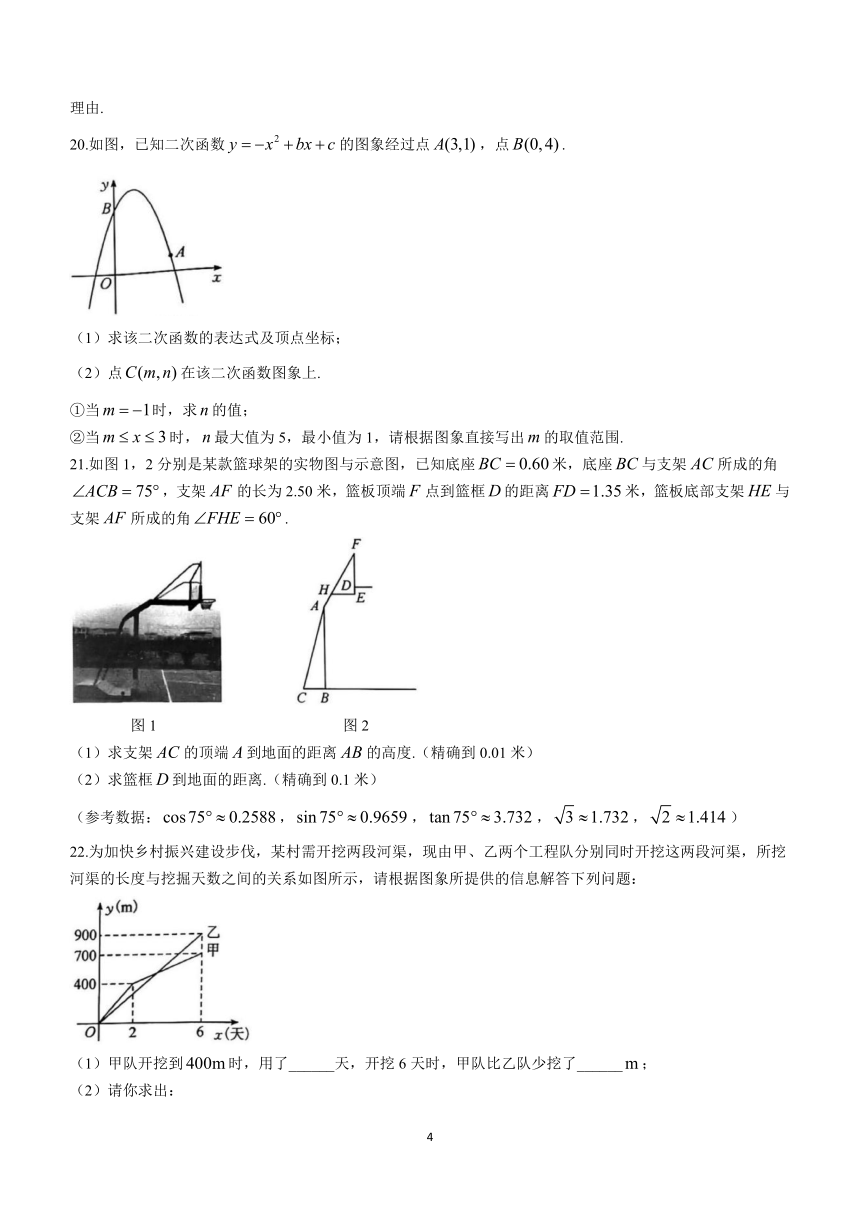
20.如图,已知二次函数的图象经过点,点.
(1)求该二次函数的表达式及顶点坐标;
(2)点在该二次函数图象上.
①当时,求的值;
②当时,最大值为5,最小值为1,请根据图象直接写出的取值范围.
21.如图1,2分别是某款篮球架的实物图与示意图,已知底座米,底座与支架所成的角,支架的长为2.50米,篮板顶端点到篮框的距离米,篮板底部支架与支架所成的角.
图1 图2
(1)求支架的顶端到地面的距离的高度.(精确到0.01米)
(2)求篮框到地面的距离.(精确到0.1米)
(参考数据:,,,,)
22.为加快乡村振兴建设步伐,某村需开挖两段河渠,现由甲、乙两个工程队分别同时开挖这两段河渠,所挖河渠的长度与挖掘天数之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)甲队开挖到时,用了______天,开挖6天时,甲队比乙队少挖了______;
(2)请你求出:
①甲队在的时段内,与之间的函数关系式;
②乙队在的时段内,与之间的函数关系式;
③当为何值时,甲、乙两队在施工过程中所挖河渠的长度相差?
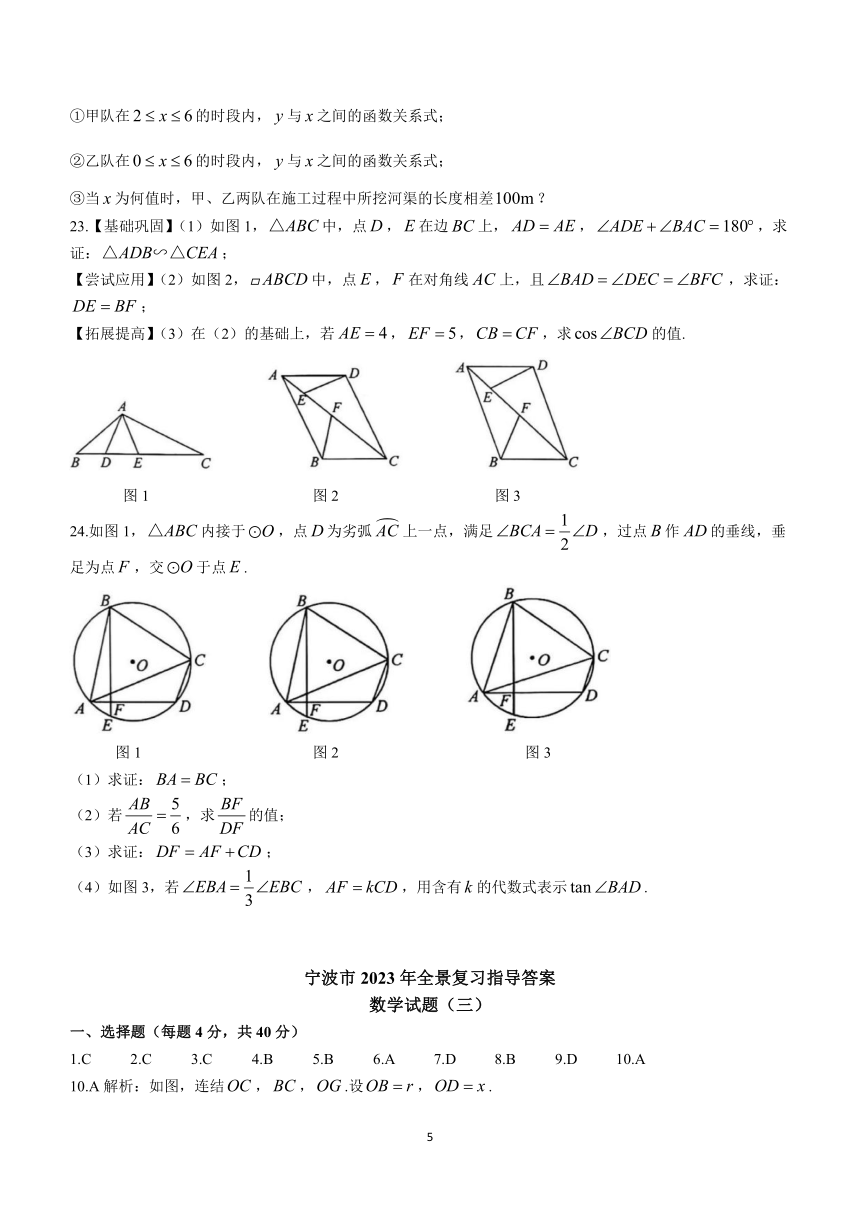
23.【基础巩固】(1)如图1,中,点,在边上,,,求证:;
【尝试应用】(2)如图2,中,点,在对角线上,且,求证:;
【拓展提高】(3)在(2)的基础上,若,,,求的值.
图1 图2 图3
24.如图1,内接于,点为劣弧上一点,满足,过点作的垂线,垂足为点,交于点.
图1 图2 图3
(1)求证:;
(2)若,求的值;
(3)求证:;
(4)如图3,若,,用含有的代数式表示.
宁波市2023年全景复习指导答案
数学试题(三)
一、选择题(每题4分,共40分)
1.C 2.C 3.C 4.B 5.B 6.A 7.D 8.B 9.D 10.A
10.A解析:如图,连结,,.设,.
与相切于点,,
.
则.
在和中,
,
即,
整理得,
要求矩形的面积,只需知道的距离.
故选A.
二、填空题(每题5分,共30分)
11.(答案不唯一) 12. 13.
14.-3 15.6.5或 16.;
16.,解析:,,
,
,.
过点,点,点作轴,轴,轴,如图.
则.
易证,,
,,
,
,解得.
,.
三、解答题(本大题有8小题,共80分)
17.解:(1)原式.
(2)解不等式①得:,
解不等式②得:,
故不等式组的解集为.
18.解:(1)如图1所示,四边形即为所求.
(2)如图2所示,即为所求.
图1 图2
19.解:(1)(吨).
故答案为:21;
(2)①②;
(3)不合理,选取的,,这三个月的当地月平均气温都比较高,这三个月的月平均用水量都比较多,这样选取的样本缺乏代表性.
20.解:(1)二次函数的图象过点,点,
,解得
该二次函数为.
,
顶点为.
(2)①当时,点在二次函数图象上
.
②当时,最大值为5.最小值为1.
顶点坐标为,当时..
根据二次函数对称性得.
21.解:(1)由题意得:在中,,
(米),
的高度为2.24米;
(2)如图,延长交射线于点,过点作于点.
,,,
四边形是矩形,
(米).
,则,
.
在中,(米),
(米),
篮框到地面的距离约为3.1米;
22.解:(1)由图象可得,
甲队开挖到时,用了2天,开挖6天时,
甲队比乙队少挖了,
故答案为:2,200;
(2)①甲队在的时段内,设与之间的函数关系式为.
点,在该函数图象上,
解得
甲队在的时段内,与之间的函数关系式是;
②乙队在的时段内,设与之间的函数关系式为.
点在该函数图象上,
,解得,
乙队在的时段内,与之间的函数关系式是;
③当时,甲、乙两队在施工过程中所挖河渠的长度相差;
当时,,
解得,
当为2或时,甲、乙两队在施工过程中所挖河渠的长度相差.
23.证明:(1),.
,,
,同理,.
;
(2)如图,截取,
易得,
即,
.
(3)如上图,,
.
由(1)可得,,
,
.
又易得,且,
,
即,
,
.
24.证明:(1)设,则,
而,,
即,.
(2)如图1,连结,连结并延长交于点,则,即.
,,.
,
.
图1 图2
(3)如图2,在上截取,则.
设,则,且,
,
,.
(4)如图3,连结并延长交于点,交于点.则.
图3
,.
设,则,
由(3)可得,,
又,,
即.
设,则,,
.
数学试题
一、选择题(每小题4分,共40分.在每小题给出的四个选项中,只有一项符合题目要求)
1.下列各数中,的相反数的倒数是( )
A.4 B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.我国神舟十三号载人飞船和航天员乘组于2022年4月16日返回地球,结束了183天的在轨飞行从2003年神舟五号载人飞船上天以来,我国已有13位航天员出征太空,绕地球飞行共约2.32亿公里.将数据232000000用科学记数法表示为( )
A. B. C. D.
4.如图所示,几何体的左视图是( )
A. B. C. D.
5.下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩(单位:)的平均数和方差.要从中选择一名成绩较高且发挥稳定的运动员参加决赛,最合适的运动员是( )
甲 乙 丙 丁
平均数 350 376 350 376
方差 13.5 2.4 5.4 12.5
A.甲 B.乙 C.丙 D.丁
6.圆锥的侧面积为,母线长为4,则它的底面半径为( )
A.2 B.1 C.3 D.4
7.如图.中,,点是的重心,连结并延长交于点,连结并延长交于点,连结.若,,则的长为( )
A.5 B.4 C.3 D.2
8.《九章算术》是中国古代重要的数学著作,其中有这样一道题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗,问醇、行酒各得几何?”译文:今有醇酒(优质酒)1斗,价格50钱;行酒(勾兑酒)1斗,价格10钱.现有30钱,买2斗酒,问能买醇酒、行酒各多少斗?设能买醇酒斗,行酒斗,可列二元一次方程组为( )
A. B. C. D.
9.在平面直角坐标系中,将二次函数的图象平移,使平移后的图象经过原点.设平移后的图象对应的函数表达式为,当时,随的增大而减小,则的取值范围为( )
A. B. C. D.
10.如图,以为直径的半圆与矩形的边相切于点,边与半圆交于点.要求矩形的面积,只需要知道下列哪两个点之间的距离( )
A.点与点 B.点与点 C.点与点 D.点与点
二、填空题(每小题5分,共30分)
11.请写出一个大于且小于1的无理数:______.
12.分解因式:______.
13.一个不透明的袋子中装有3个红球和2个白球,这些球除颜色不同外,其余均相同,从中任意摸出一个球,这个球是白球的概率为______.
14.定义一种新运算:对于任意的非零实数,,.若,则的值为______.
15.如图,中,,,,,点是线段上一动点,当半径为6的与的一边相切时,的长为______.
16.如图,的顶点,分别落在反比例函数和的图象上,连结,将沿着翻折,点的对应点恰好落在的图象上,与交于点.已知的面积为,,则的值为______,的值为______.
三、解答题(本大题有8小题,17~19题每题8分,20~22题每题10分,23题12分,24题14分,共80分)
17.(1)计算:.
(2)解不等式组
18.图1、图2是的网格,网格中每个小正方形的边长均为1,请按要求画出下列图形,所画图形的各个顶点均在小正方形的顶点上.
图1 图2
(1)在图1中画出以为一边的成中心对称的四边形,使其面积为12;
(2)在图2中画出一个以为一边的,使其是面积为的轴对称图形.
19.用水问题一直是人民关注的热点问题,为此,小明随机抽取自己家中一年5个月的月用水量(单位:吨),并对每个月的月平均气温(单位:℃)进行了统计,得到下列统计图
(1)小明家这5个月的月平均用水量为______吨;
(2)下列推断:①当地当年月平均气温的众数是;
②当地当年月平均气温的中位数为;
③小明家这5个月的月用水量随着月平均气温的变化而变化,温度越高,月用水量越大.所有合理推断的序号是______;
(3)如果用小明家5月、7月、9月这三个月的月平均用水量估计当年的用水总量,你认为是否合理?并说明理由.
20.如图,已知二次函数的图象经过点,点.
(1)求该二次函数的表达式及顶点坐标;
(2)点在该二次函数图象上.
①当时,求的值;
②当时,最大值为5,最小值为1,请根据图象直接写出的取值范围.
21.如图1,2分别是某款篮球架的实物图与示意图,已知底座米,底座与支架所成的角,支架的长为2.50米,篮板顶端点到篮框的距离米,篮板底部支架与支架所成的角.
图1 图2
(1)求支架的顶端到地面的距离的高度.(精确到0.01米)
(2)求篮框到地面的距离.(精确到0.1米)
(参考数据:,,,,)
22.为加快乡村振兴建设步伐,某村需开挖两段河渠,现由甲、乙两个工程队分别同时开挖这两段河渠,所挖河渠的长度与挖掘天数之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)甲队开挖到时,用了______天,开挖6天时,甲队比乙队少挖了______;
(2)请你求出:
①甲队在的时段内,与之间的函数关系式;
②乙队在的时段内,与之间的函数关系式;
③当为何值时,甲、乙两队在施工过程中所挖河渠的长度相差?
23.【基础巩固】(1)如图1,中,点,在边上,,,求证:;
【尝试应用】(2)如图2,中,点,在对角线上,且,求证:;
【拓展提高】(3)在(2)的基础上,若,,,求的值.
图1 图2 图3
24.如图1,内接于,点为劣弧上一点,满足,过点作的垂线,垂足为点,交于点.
图1 图2 图3
(1)求证:;
(2)若,求的值;
(3)求证:;
(4)如图3,若,,用含有的代数式表示.
宁波市2023年全景复习指导答案
数学试题(三)
一、选择题(每题4分,共40分)
1.C 2.C 3.C 4.B 5.B 6.A 7.D 8.B 9.D 10.A
10.A解析:如图,连结,,.设,.
与相切于点,,
.
则.
在和中,
,
即,
整理得,
要求矩形的面积,只需知道的距离.
故选A.
二、填空题(每题5分,共30分)
11.(答案不唯一) 12. 13.
14.-3 15.6.5或 16.;
16.,解析:,,
,
,.
过点,点,点作轴,轴,轴,如图.
则.
易证,,
,,
,
,解得.
,.
三、解答题(本大题有8小题,共80分)
17.解:(1)原式.
(2)解不等式①得:,
解不等式②得:,
故不等式组的解集为.
18.解:(1)如图1所示,四边形即为所求.
(2)如图2所示,即为所求.
图1 图2
19.解:(1)(吨).
故答案为:21;
(2)①②;
(3)不合理,选取的,,这三个月的当地月平均气温都比较高,这三个月的月平均用水量都比较多,这样选取的样本缺乏代表性.
20.解:(1)二次函数的图象过点,点,
,解得
该二次函数为.
,
顶点为.
(2)①当时,点在二次函数图象上
.
②当时,最大值为5.最小值为1.
顶点坐标为,当时..
根据二次函数对称性得.
21.解:(1)由题意得:在中,,
(米),
的高度为2.24米;
(2)如图,延长交射线于点,过点作于点.
,,,
四边形是矩形,
(米).
,则,
.
在中,(米),
(米),
篮框到地面的距离约为3.1米;
22.解:(1)由图象可得,
甲队开挖到时,用了2天,开挖6天时,
甲队比乙队少挖了,
故答案为:2,200;
(2)①甲队在的时段内,设与之间的函数关系式为.
点,在该函数图象上,
解得
甲队在的时段内,与之间的函数关系式是;
②乙队在的时段内,设与之间的函数关系式为.
点在该函数图象上,
,解得,
乙队在的时段内,与之间的函数关系式是;
③当时,甲、乙两队在施工过程中所挖河渠的长度相差;
当时,,
解得,
当为2或时,甲、乙两队在施工过程中所挖河渠的长度相差.
23.证明:(1),.
,,
,同理,.
;
(2)如图,截取,
易得,
即,
.
(3)如上图,,
.
由(1)可得,,
,
.
又易得,且,
,
即,
,
.
24.证明:(1)设,则,
而,,
即,.
(2)如图1,连结,连结并延长交于点,则,即.
,,.
,
.
图1 图2
(3)如图2,在上截取,则.
设,则,且,
,
,.
(4)如图3,连结并延长交于点,交于点.则.
图3
,.
设,则,
由(3)可得,,
又,,
即.
设,则,,
.
同课章节目录
