2023年山东省泰安市泰山实验中学初中学业水平数学模拟预测题(含答案)
文档属性
| 名称 | 2023年山东省泰安市泰山实验中学初中学业水平数学模拟预测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 08:31:16 | ||
图片预览




文档简介
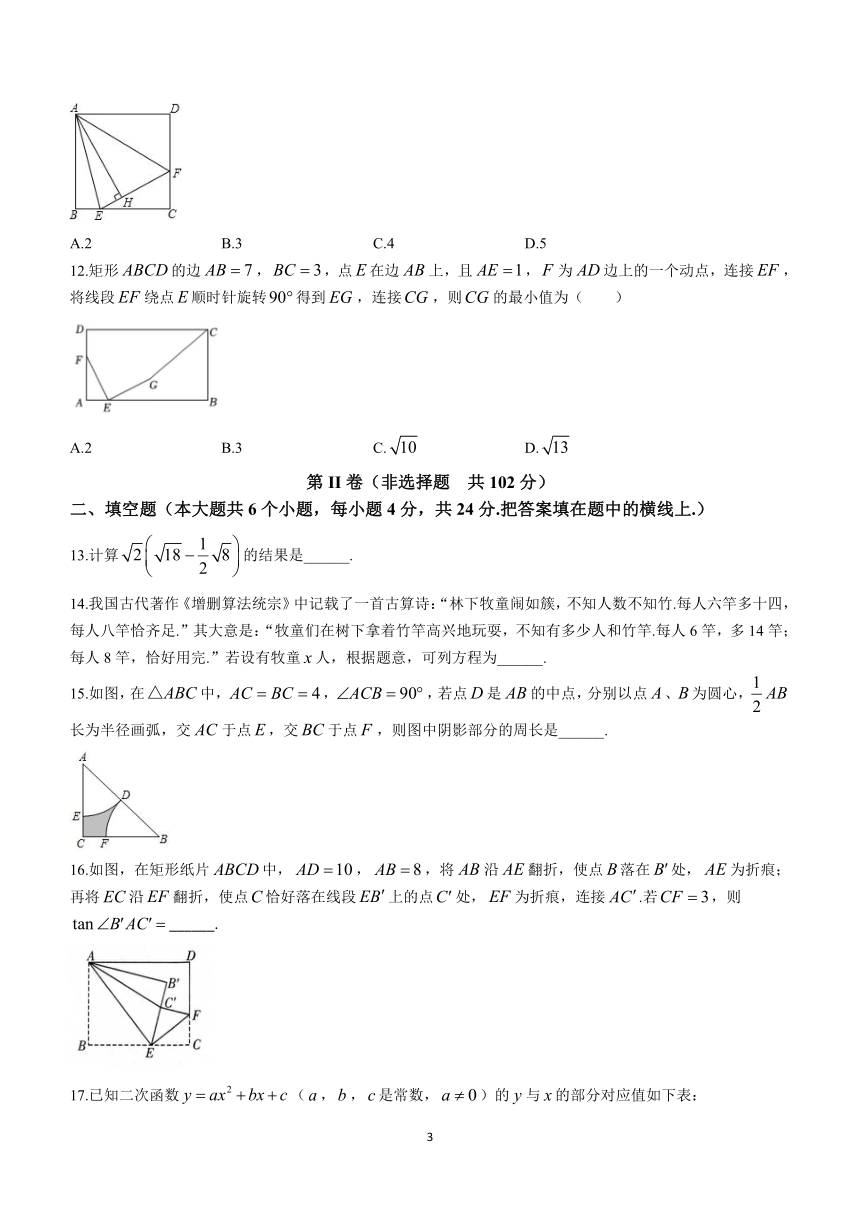
泰安市2023年初中学业水平数学押题
本试题分第I卷(选择题)和第II卷(非选择题)两部分,第I卷1至3页,第II卷3至8页,共150分,考试时间120分钟
注意事项:
1.答题前请考生仔细阅读答题卡上的注意事项,并务必按照相关要求作答。
2.考试结束后,监考人员将本试卷和答题卡一并收回。
第I卷(选择题 共48分)
一、选择题(本大题共12个小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求.)
1.下列各数,,,,,,中,无理数有( )
A.2个 B.3个 C.4个 D.5个
2.如图,是由若干个相同的小立方体搭成的几何体的主视图和左视图,则搭成这个几何体的小立方体的个数不可能是( )
A.3 B.4 C.5 D.6
3.下列计算中,结果正确的是( )
A. B.
C. D.
4.1968年科学家发现世界上最小的物质是夸克,物质就是由这种极其小的物质而构成的,夸克有多小呢?它的大小是1介米,约为原子核的百万分之一.百万分之一用科学记数法表示为( )
A. B. C. D.
5.如图,将一副三角尺按图中所示位置摆放,点在上,,,,,.则的度数是( )
A. B. C. D.
6.甲乙两台机床同时生产同一种零件,在某周的工作日内,两台机床每天生产次品的个数整理成甲、乙两组数据,如表,关于以上数据,下列说法正确的是( )
星期一 星期二 星期三 星期四 星期五
甲 2 0 4 3 2
乙 1 3 4 0 4
A.甲、乙的众数相同 B.甲、乙的中位数相同
C.甲的平均数大于乙的平均数 D.甲的方差小于乙的方差
7.如图,点,,是上的三点.若,,则的大小为( )
A. B. C. D.
8.如果关于的一元二次方程有两个相等的实数根,则直线必定经过的象限是( )
A.一、二、三 B.一、二、四 C.二、三、四 D.一、三、四
9.如图,是的弦,等边三角形的边与相切于点,且,连接,,,.若,,则的长是( )
A. B. C. D.
10.如图,胡同左右两侧是竖直的墙,一架米长的梯子斜靠在右侧墙壁上,测得梯子与地面的夹角为,此时梯子顶端恰巧与墙壁顶端重合.因梯子阻碍交通,故将梯子底端向右移动一段距离到达处,此时测得梯子与地面的夹角为,则胡同左侧的通道拓宽了( )
A.米 B.3米 C.米 D.米
11.如图,在正方形中,,,分别是边,上的点,连接、、,过作于点.若,那么下列结论:①平分;②;③;④;⑤的周长为2.其中正确结论的个数是( )
A.2 B.3 C.4 D.5
12.矩形的边,,点在边上,且,为边上的一个动点,连接,将线段绕点顺时针旋转得到,连接,则的最小值为( )
A.2 B.3 C. D.
第II卷(非选择题 共102分)
二、填空题(本大题共6个小题,每小题4分,共24分.把答案填在题中的横线上.)
13.计算的结果是______.
14.我国古代著作《增删算法统宗》中记载了一首古算诗:“林下牧童闹如簇,不知人数不知竹.每人六竿多十四,每人八竿恰齐足.”其大意是:“牧童们在树下拿着竹竿高兴地玩耍,不知有多少人和竹竿.每人6竿,多14竿;每人8竿,恰好用完.”若设有牧童人,根据题意,可列方程为______.
15.如图,在中,,,若点是的中点,分别以点、为圆心,长为半径画弧,交于点,交于点,则图中阴影部分的周长是______.
16.如图,在矩形纸片中,,,将沿翻折,使点落在处,为折痕;再将沿翻折,使点恰好落在线段上的点处,为折痕,连接.若,则______.
17.已知二次函数(,,是常数,)的与的部分对应值如下表:
0 2
6 0 6
下列结论:①;②当时,的值随的增大而减小;③方程有两个不相等的实数根.④当时,函数有最小值.其中,正确结论的序号是______(把所有正确结论的序号都填上).
18.若,则称是以10为底的对数.记作:.例如:,则;,则.对数运算满足:当,时,.例如:,则的值为______.
三、解答题(本大题共7个小题,共78分,解答应写出文字说明、推理过程或演算步骤。)
19.(10分)(1)先化简,再求值:,其中
(2)解不等式组:并写出它的所有整数解.
20.(共10分)如图,已知反比例函数的图象与反比例函数的图象关于轴对称,,是函数图象上的两点,连接,点是函数图象上的一点,连接,.
(1)求,的值;
(2)求所在直线表达式;
(3)求的面积.
21.(10分)某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整统计图.
学生最喜要节目的人数 学生最喜要节目的人数
条形统计图 扇形统计图
请你根据图中信息,回答下列问题:
(1)本次共调查了______名学生.
(2)在扇形统计图中,“歌曲”所在扇形的圆心角等于______度.
(3)补全条形统计图(标注频数).
(4)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数为______人.
(5)九年一班和九年二班各有2名学生擅长舞蹈,学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排,那么抽取的2名学生恰好来自同一个班级的概率是多少.
22.(共10分)某汽车贸易公司销售、两种型号的新能源汽车,型车进货价格为每台12万元,型车进货价格为每台15万元,该公司销售2台型车和5台型车,可获利3.1万元,销售1台型车和2台型车,可获利1.3万元.
(1)求销售一台型、一台型新能源汽车的利润各是多少万元?
(2)该公司准备用不超过300万元资金,采购、两种新能源汽车共22台,问最少需要采购型新能源汽车多少台?
23.(共12分)如图,四边形内接于,对角线为的直径,过点作的垂线交的延长线于点,点为的中点,连接,,.
(1)求的度数;
(2)求证:是的切线;
(3)若,求的值.
24.(共13分)在中,,,点是射线上的一动点(不与点,重合)连接,在的右侧以为斜边作等腰直角三角形,点是的中点,连接.
【问题发现】
图(1) 图(2) 备用图
(1)如图(1),当点是的中点时,线段与的数量关系是______.与的位置关系是______.
【猜想论证】
(2)如图(2),当点在边上且不是的中点时,(1)中的结论是否仍然成立?若成立,请仅就图(2)中的情况给出证明;若不成立,请说明理由.
【拓展应用】
(3)若,其他条件不变,连接、.当是等边三角形时,请直接写出的面积.
25.(共13分)抛物线与轴交于,两点(点在点的左边),与轴正半轴交于点.
图1 图2
(1)如图1,若,,
①求抛物线的解析式;
②为抛物线上一点,连接、,若,求点的坐标;
如图2,为轴下方抛物线上一点,连,,若,求点的纵坐标.
泰安市2023年初中学业水平数学押题
九年级数学参考答案
阅卷须知:
1.为便于阅卷,本试卷答案中有关解答题的推导步骤写得较为详细,阅卷时,只要考生将主要过程正确写出即可;
2.若考生的解法与给出的解法不同,正确者相应给分;
一、选择题(本大题共12个小题,每小题4分,共48分.)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D B B C D B B C D D D
二、填空题(本大题共6个小题,每小题4分,共24分。)
13.4 14. 15. 16. 17.①②③ 18.1
三、解答题
19.(1)解:
当时,原式
(2)解不等式①得:
解不等式②得:
不等式组的解集为:
它的所有整数解为:,,
20解:(1)由,是函数图象上的两点,
,,.
的图象和的图象关于轴对称,
点关于轴的对称点在的图象上,
,,
由点是函数图象上的一点,.
(2)设所在直线的表达式为,
将,分别代入,得
解这个二元一次方程组,得.
所在直线表达式为:
(3)自,,三点分别向轴作垂线,垂足分别为,,,
,,,,,.
21.解:(1),
所以本次共调查了50名学生;
(2)在扇形统计图中,“歌曲”所在扇形的圆心角的度数;
(3)最喜欢舞蹈类的人数为(人),
补全条形统计图为:
学生最喜爱节目的人数条形统计图
(4),
估计该校2000名学生中最喜爱小品的人数为640人;
故答案为;;;
(5)画树状图为:
共有12种等可能的结果数,其中抽取的2名学生恰好来自同一个班级的结果数为4,所以抽取的2名学生恰好来自同一个班级的概率.
22.解:(1)设销售一台型新能源汽车的利润是万元,销售一台型新能源汽车的利润是万元,
依题意得:,解得:.
答:销售一台型新能源汽车的利润是0.3万元,销售一台型新能源汽车的利润0.5万元.
(2)设需要采购型新能源汽车台,则采购型新能源汽车台,
依题意得:,
解得:.
答:最少需要采购型新能源汽车10台.
23.(1)解:对角线为的直径,
,;
(2)证明:连接,
,是的中点,
,,
,,
,
,是的切线;
(3)解:如图所示:可得,
,,
,
又,,
,
,设,则,
则,
期,
整理得:,
解得:或(负数舍去),
则,
故.
24.解:(1)如图1中,
图(1)
,,,
,,
,,
, 点在线段上,
,,,
故答案为,
(2)结论仍然成立:
理由:如图2中,延长到,使得,连接,.
图(2)
,,,
,,
,,
,,
,,
,,,
,,,,
,,
(3)如图3-2中,当是等边三角形时,过点作于.
图3-2
可求:,,
,
综上所述,满足条件的的面积.
25.解:(1)①,代入得:
,解得
②过点作直线,过点作交于点,过点作交于点,
,,
,
,
设点坐标为
解得,,(舍去),把代入,,
(2)作轴,垂足为
,
设点坐标为
,即,
为轴下方抛物线上一点,即且化简得,,
的纵坐标.
本试题分第I卷(选择题)和第II卷(非选择题)两部分,第I卷1至3页,第II卷3至8页,共150分,考试时间120分钟
注意事项:
1.答题前请考生仔细阅读答题卡上的注意事项,并务必按照相关要求作答。
2.考试结束后,监考人员将本试卷和答题卡一并收回。
第I卷(选择题 共48分)
一、选择题(本大题共12个小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求.)
1.下列各数,,,,,,中,无理数有( )
A.2个 B.3个 C.4个 D.5个
2.如图,是由若干个相同的小立方体搭成的几何体的主视图和左视图,则搭成这个几何体的小立方体的个数不可能是( )
A.3 B.4 C.5 D.6
3.下列计算中,结果正确的是( )
A. B.
C. D.
4.1968年科学家发现世界上最小的物质是夸克,物质就是由这种极其小的物质而构成的,夸克有多小呢?它的大小是1介米,约为原子核的百万分之一.百万分之一用科学记数法表示为( )
A. B. C. D.
5.如图,将一副三角尺按图中所示位置摆放,点在上,,,,,.则的度数是( )
A. B. C. D.
6.甲乙两台机床同时生产同一种零件,在某周的工作日内,两台机床每天生产次品的个数整理成甲、乙两组数据,如表,关于以上数据,下列说法正确的是( )
星期一 星期二 星期三 星期四 星期五
甲 2 0 4 3 2
乙 1 3 4 0 4
A.甲、乙的众数相同 B.甲、乙的中位数相同
C.甲的平均数大于乙的平均数 D.甲的方差小于乙的方差
7.如图,点,,是上的三点.若,,则的大小为( )
A. B. C. D.
8.如果关于的一元二次方程有两个相等的实数根,则直线必定经过的象限是( )
A.一、二、三 B.一、二、四 C.二、三、四 D.一、三、四
9.如图,是的弦,等边三角形的边与相切于点,且,连接,,,.若,,则的长是( )
A. B. C. D.
10.如图,胡同左右两侧是竖直的墙,一架米长的梯子斜靠在右侧墙壁上,测得梯子与地面的夹角为,此时梯子顶端恰巧与墙壁顶端重合.因梯子阻碍交通,故将梯子底端向右移动一段距离到达处,此时测得梯子与地面的夹角为,则胡同左侧的通道拓宽了( )
A.米 B.3米 C.米 D.米
11.如图,在正方形中,,,分别是边,上的点,连接、、,过作于点.若,那么下列结论:①平分;②;③;④;⑤的周长为2.其中正确结论的个数是( )
A.2 B.3 C.4 D.5
12.矩形的边,,点在边上,且,为边上的一个动点,连接,将线段绕点顺时针旋转得到,连接,则的最小值为( )
A.2 B.3 C. D.
第II卷(非选择题 共102分)
二、填空题(本大题共6个小题,每小题4分,共24分.把答案填在题中的横线上.)
13.计算的结果是______.
14.我国古代著作《增删算法统宗》中记载了一首古算诗:“林下牧童闹如簇,不知人数不知竹.每人六竿多十四,每人八竿恰齐足.”其大意是:“牧童们在树下拿着竹竿高兴地玩耍,不知有多少人和竹竿.每人6竿,多14竿;每人8竿,恰好用完.”若设有牧童人,根据题意,可列方程为______.
15.如图,在中,,,若点是的中点,分别以点、为圆心,长为半径画弧,交于点,交于点,则图中阴影部分的周长是______.
16.如图,在矩形纸片中,,,将沿翻折,使点落在处,为折痕;再将沿翻折,使点恰好落在线段上的点处,为折痕,连接.若,则______.
17.已知二次函数(,,是常数,)的与的部分对应值如下表:
0 2
6 0 6
下列结论:①;②当时,的值随的增大而减小;③方程有两个不相等的实数根.④当时,函数有最小值.其中,正确结论的序号是______(把所有正确结论的序号都填上).
18.若,则称是以10为底的对数.记作:.例如:,则;,则.对数运算满足:当,时,.例如:,则的值为______.
三、解答题(本大题共7个小题,共78分,解答应写出文字说明、推理过程或演算步骤。)
19.(10分)(1)先化简,再求值:,其中
(2)解不等式组:并写出它的所有整数解.
20.(共10分)如图,已知反比例函数的图象与反比例函数的图象关于轴对称,,是函数图象上的两点,连接,点是函数图象上的一点,连接,.
(1)求,的值;
(2)求所在直线表达式;
(3)求的面积.
21.(10分)某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整统计图.
学生最喜要节目的人数 学生最喜要节目的人数
条形统计图 扇形统计图
请你根据图中信息,回答下列问题:
(1)本次共调查了______名学生.
(2)在扇形统计图中,“歌曲”所在扇形的圆心角等于______度.
(3)补全条形统计图(标注频数).
(4)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数为______人.
(5)九年一班和九年二班各有2名学生擅长舞蹈,学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排,那么抽取的2名学生恰好来自同一个班级的概率是多少.
22.(共10分)某汽车贸易公司销售、两种型号的新能源汽车,型车进货价格为每台12万元,型车进货价格为每台15万元,该公司销售2台型车和5台型车,可获利3.1万元,销售1台型车和2台型车,可获利1.3万元.
(1)求销售一台型、一台型新能源汽车的利润各是多少万元?
(2)该公司准备用不超过300万元资金,采购、两种新能源汽车共22台,问最少需要采购型新能源汽车多少台?
23.(共12分)如图,四边形内接于,对角线为的直径,过点作的垂线交的延长线于点,点为的中点,连接,,.
(1)求的度数;
(2)求证:是的切线;
(3)若,求的值.
24.(共13分)在中,,,点是射线上的一动点(不与点,重合)连接,在的右侧以为斜边作等腰直角三角形,点是的中点,连接.
【问题发现】
图(1) 图(2) 备用图
(1)如图(1),当点是的中点时,线段与的数量关系是______.与的位置关系是______.
【猜想论证】
(2)如图(2),当点在边上且不是的中点时,(1)中的结论是否仍然成立?若成立,请仅就图(2)中的情况给出证明;若不成立,请说明理由.
【拓展应用】
(3)若,其他条件不变,连接、.当是等边三角形时,请直接写出的面积.
25.(共13分)抛物线与轴交于,两点(点在点的左边),与轴正半轴交于点.
图1 图2
(1)如图1,若,,
①求抛物线的解析式;
②为抛物线上一点,连接、,若,求点的坐标;
如图2,为轴下方抛物线上一点,连,,若,求点的纵坐标.
泰安市2023年初中学业水平数学押题
九年级数学参考答案
阅卷须知:
1.为便于阅卷,本试卷答案中有关解答题的推导步骤写得较为详细,阅卷时,只要考生将主要过程正确写出即可;
2.若考生的解法与给出的解法不同,正确者相应给分;
一、选择题(本大题共12个小题,每小题4分,共48分.)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D B B C D B B C D D D
二、填空题(本大题共6个小题,每小题4分,共24分。)
13.4 14. 15. 16. 17.①②③ 18.1
三、解答题
19.(1)解:
当时,原式
(2)解不等式①得:
解不等式②得:
不等式组的解集为:
它的所有整数解为:,,
20解:(1)由,是函数图象上的两点,
,,.
的图象和的图象关于轴对称,
点关于轴的对称点在的图象上,
,,
由点是函数图象上的一点,.
(2)设所在直线的表达式为,
将,分别代入,得
解这个二元一次方程组,得.
所在直线表达式为:
(3)自,,三点分别向轴作垂线,垂足分别为,,,
,,,,,.
21.解:(1),
所以本次共调查了50名学生;
(2)在扇形统计图中,“歌曲”所在扇形的圆心角的度数;
(3)最喜欢舞蹈类的人数为(人),
补全条形统计图为:
学生最喜爱节目的人数条形统计图
(4),
估计该校2000名学生中最喜爱小品的人数为640人;
故答案为;;;
(5)画树状图为:
共有12种等可能的结果数,其中抽取的2名学生恰好来自同一个班级的结果数为4,所以抽取的2名学生恰好来自同一个班级的概率.
22.解:(1)设销售一台型新能源汽车的利润是万元,销售一台型新能源汽车的利润是万元,
依题意得:,解得:.
答:销售一台型新能源汽车的利润是0.3万元,销售一台型新能源汽车的利润0.5万元.
(2)设需要采购型新能源汽车台,则采购型新能源汽车台,
依题意得:,
解得:.
答:最少需要采购型新能源汽车10台.
23.(1)解:对角线为的直径,
,;
(2)证明:连接,
,是的中点,
,,
,,
,
,是的切线;
(3)解:如图所示:可得,
,,
,
又,,
,
,设,则,
则,
期,
整理得:,
解得:或(负数舍去),
则,
故.
24.解:(1)如图1中,
图(1)
,,,
,,
,,
, 点在线段上,
,,,
故答案为,
(2)结论仍然成立:
理由:如图2中,延长到,使得,连接,.
图(2)
,,,
,,
,,
,,
,,
,,,
,,,,
,,
(3)如图3-2中,当是等边三角形时,过点作于.
图3-2
可求:,,
,
综上所述,满足条件的的面积.
25.解:(1)①,代入得:
,解得
②过点作直线,过点作交于点,过点作交于点,
,,
,
,
设点坐标为
解得,,(舍去),把代入,,
(2)作轴,垂足为
,
设点坐标为
,即,
为轴下方抛物线上一点,即且化简得,,
的纵坐标.
同课章节目录
