物理人教版(2019)必修第二册8.2重力势能(共16张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册8.2重力势能(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-28 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第八章 机械能守恒定律
2 重力势能
小心高空坠物
问题.运用物理学知识分析,为什么要当心高空落物?
思考.如何定量描述物体的重力势能?
重力做功的特点
h2
h1
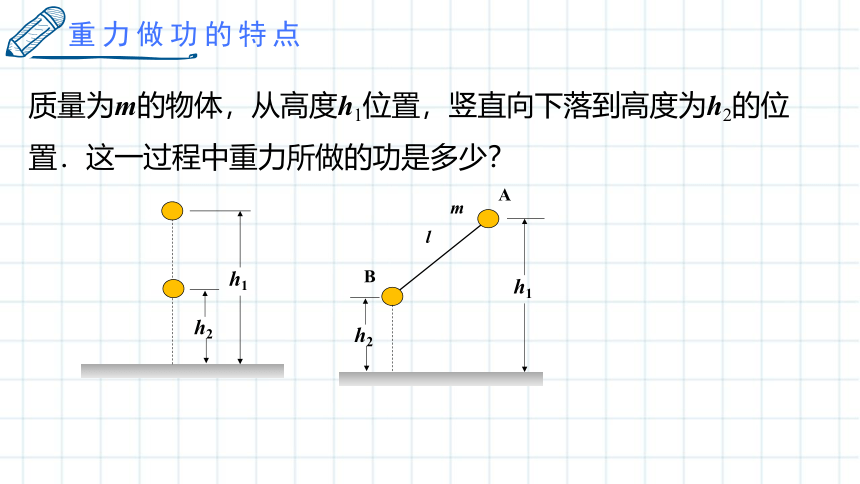
质量为m的物体,从高度h1位置,竖直向下落到高度为h2的位置.这一过程中重力所做的功是多少?
B
l
h1
h2
m
A
质量为m的物体从高度h1处的A点沿曲线运动到高度h2的B点.这一过程中重力所做的功是多少?
重力做功的特点
A
B
h1
h2
m
WG=mgΔh1+mgΔh2 + ···
=mg(Δh1 +Δh2 + ···)
=mgh=mgh1-mgh2
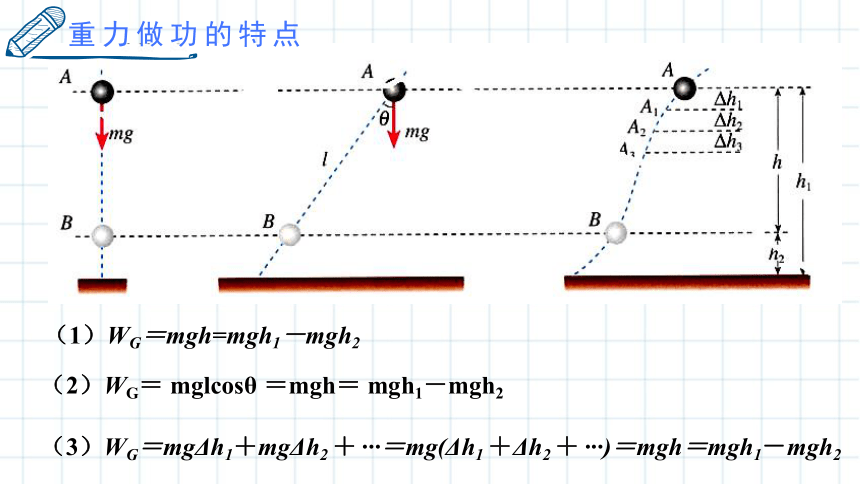
(1)WG=mgh=mgh1-mgh2
(2)WG= mglcosθ =mgh= mgh1-mgh2
(3)WG=mgΔh1+mgΔh2 + ···=mg(Δh1 +Δh2 + ···)=mgh=mgh1-mgh2
重力做功的特点
分析表明重力做功只跟它的起点和终点的位置的高度差有关,而跟物体运动的路径无关。
WG =mgh1-mgh2
“mgh”具有特殊的意义
它与重力做功有关,又与重力势能的基本特征一致
物理学上把mgh叫做重力势能
重力势能
1.定义:物体所受重力mg与所处高度h的乘积叫做物体的重力势能。用Ep表示。
2.表达式:
Ep = mgh
3.单位:焦耳,符号为J
4.重力势能是标量,是状态量
5.重力做功和重力势能变化的关系:
WG=EP1-EP2
重力做正功,WG>0,即EP1>EP2,重力势能减少;
重力做负功,WG<0,即EP16.重力势能是地球与物体所组成的“系统”所共有的,而不是物体单独具有的。
巩固提升
如图所示,质量为m的小球从曲面左侧上的A点滚下,经过最低点后滚到曲面右侧上的B点。已知A点距最低点的高度为h1,B点距最低点的高度为h2。求小球从A点滚到B点的过程中,重力做了多少功?小球的重力势能变化了多少?
h2
h1
A
B
1.重力势能总是相对参考平面(重力势能为0)来说的,重力势能具有相对性。
参考平面的选取是任意的
通常选择地面作为参考平面
C
互动探究,如图所示,已知AB高度h1为0.5m,BC高度h2为1m,求重为2N的小球在A点的重力势能是 J,在B点的重力势能是 J,在C点的重力势能是 J,则物体在哪一点的重力势能最大?(以B点所在的平面为零势能参考面)
2.重力势能的正负代表大小(相对参考面),不代表方向。
如图有一个质量0.2kg的小球从桌面以上高h1=1.2m的A点落到地面上的B点,桌面的高为h2=0.8m。请按要求填写下表 (g=10m/s2)。
h1
h2
A
B
参考 平面 小球在A点重力势能EpA 小球在B点重力势能EpB A→B下落过程小球重力做功WG A→B下落过程小球重力势能变化ΔEp
桌面
地面
选取不同的参考平面,物体的重力势能的数值不同。
WG、△Ep与参考面的选取无关。
比较、分析表格中的数据,有何特点?
相对性
绝对性
弹性势能
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能。
1.探究:弹性势能的大小可能与那些因素有关
弹性势能的大小与形变量、劲度系数有关
2.探究:弹簧的弹性势能与弹力做功的关系?
规定:当弹簧的长度为原长时,它的弹性势能为0。
拉伸弹簧的过程中:弹簧弹力做负功,弹性势能增加;
弹簧恢复形变的过程中:弹力做正功,弹性势能减少;
探究结论:弹力做功等于弹性势能的减少量
W=EP1-EP2
课堂小结
势能
重力势能
弹性势能
重力做功
特点:只与初末位置有关、与路径无关
公式:WG=mg△h
定义:物体由于被举高而具有的能
相对性
参考平面的选取
正负号的物理意义
重力做功与重力势能变化的关系:WG=EP1-EP2
定义:发生弹性形变的物体的各个部分之间,由于有弹力的相互作用而具有的能
相关因素
形变量
劲度系数
致谢
第八章 机械能守恒定律
2 重力势能
小心高空坠物
问题.运用物理学知识分析,为什么要当心高空落物?
思考.如何定量描述物体的重力势能?
重力做功的特点
h2
h1
质量为m的物体,从高度h1位置,竖直向下落到高度为h2的位置.这一过程中重力所做的功是多少?
B
l
h1
h2
m
A
质量为m的物体从高度h1处的A点沿曲线运动到高度h2的B点.这一过程中重力所做的功是多少?
重力做功的特点
A
B
h1
h2
m
WG=mgΔh1+mgΔh2 + ···
=mg(Δh1 +Δh2 + ···)
=mgh=mgh1-mgh2
(1)WG=mgh=mgh1-mgh2
(2)WG= mglcosθ =mgh= mgh1-mgh2
(3)WG=mgΔh1+mgΔh2 + ···=mg(Δh1 +Δh2 + ···)=mgh=mgh1-mgh2
重力做功的特点
分析表明重力做功只跟它的起点和终点的位置的高度差有关,而跟物体运动的路径无关。
WG =mgh1-mgh2
“mgh”具有特殊的意义
它与重力做功有关,又与重力势能的基本特征一致
物理学上把mgh叫做重力势能
重力势能
1.定义:物体所受重力mg与所处高度h的乘积叫做物体的重力势能。用Ep表示。
2.表达式:
Ep = mgh
3.单位:焦耳,符号为J
4.重力势能是标量,是状态量
5.重力做功和重力势能变化的关系:
WG=EP1-EP2
重力做正功,WG>0,即EP1>EP2,重力势能减少;
重力做负功,WG<0,即EP1
巩固提升
如图所示,质量为m的小球从曲面左侧上的A点滚下,经过最低点后滚到曲面右侧上的B点。已知A点距最低点的高度为h1,B点距最低点的高度为h2。求小球从A点滚到B点的过程中,重力做了多少功?小球的重力势能变化了多少?
h2
h1
A
B
1.重力势能总是相对参考平面(重力势能为0)来说的,重力势能具有相对性。
参考平面的选取是任意的
通常选择地面作为参考平面
C
互动探究,如图所示,已知AB高度h1为0.5m,BC高度h2为1m,求重为2N的小球在A点的重力势能是 J,在B点的重力势能是 J,在C点的重力势能是 J,则物体在哪一点的重力势能最大?(以B点所在的平面为零势能参考面)
2.重力势能的正负代表大小(相对参考面),不代表方向。
如图有一个质量0.2kg的小球从桌面以上高h1=1.2m的A点落到地面上的B点,桌面的高为h2=0.8m。请按要求填写下表 (g=10m/s2)。
h1
h2
A
B
参考 平面 小球在A点重力势能EpA 小球在B点重力势能EpB A→B下落过程小球重力做功WG A→B下落过程小球重力势能变化ΔEp
桌面
地面
选取不同的参考平面,物体的重力势能的数值不同。
WG、△Ep与参考面的选取无关。
比较、分析表格中的数据,有何特点?
相对性
绝对性
弹性势能
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能。
1.探究:弹性势能的大小可能与那些因素有关
弹性势能的大小与形变量、劲度系数有关
2.探究:弹簧的弹性势能与弹力做功的关系?
规定:当弹簧的长度为原长时,它的弹性势能为0。
拉伸弹簧的过程中:弹簧弹力做负功,弹性势能增加;
弹簧恢复形变的过程中:弹力做正功,弹性势能减少;
探究结论:弹力做功等于弹性势能的减少量
W=EP1-EP2
课堂小结
势能
重力势能
弹性势能
重力做功
特点:只与初末位置有关、与路径无关
公式:WG=mg△h
定义:物体由于被举高而具有的能
相对性
参考平面的选取
正负号的物理意义
重力做功与重力势能变化的关系:WG=EP1-EP2
定义:发生弹性形变的物体的各个部分之间,由于有弹力的相互作用而具有的能
相关因素
形变量
劲度系数
致谢
