第1单元扇形统计图高频考点检测卷(含答案)数学六年级下册苏教版
文档属性
| 名称 | 第1单元扇形统计图高频考点检测卷(含答案)数学六年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 715.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 15:44:41 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第1单元扇形统计图高频考点检测卷-数学六年级下册苏教版
一、选择题
1.能更清楚地看出数量增减变化情况的是( )。
A.单式统计表 B.复式统计表 C.条形统计图 D.折线统计图
2.医院统计某位病人一天的体温情况,选用( )统计图更合适。
A.扇形 B.折线 C.条形 D.都可以
3.太阳是由75%的氢和25%的氦组成的,下面( )统计图能正确表达这个信息。
A. B. C. D.
4.如图所示,初一(2)班的参加数学兴趣小组的有27人,那么参加美术小组的有( )人。
A.18 B.50 C.15 D.8
5.某班有50人,其中三好学生10人,优秀学生干部5人,在扇形统计图上表示三好学生和优秀学生干部人数的圆心角分别是( )。
A.72°,36° B.100°,50° C.80°,40° D.120°,60°
6.学校将某一年级数学考试成绩分为A、B、C、D四个等级,绘制成扇形统计图,则D等级所占的百分比是( )
A.10% B.5% C.20% D.8%
二、填空题
7.气象局要统计一个月内的气温变化情况,选用( )统计图比较合适。
8.如果要表示出学校2018年~2021年图书本数的变化情况,选择( )统计图比较合适;如果要表示出科技书的本数占学校图书总数的百分比,应选择( )统计图比较合适。
9.如图所示,六年级学生有200人。
(1)( )项目最受欢迎,喜欢这个项目的有( )人。
(2)喜欢羽毛球的学生比喜欢足球的多( )人。
(3)喜欢足球的比喜欢篮球的学生少( )%。
10.如图是尚文学校2019年六年级数学竞赛成绩,优秀的有24人,那么不及格的有( )人。
11.如图,已知黄瓜的种植面积是2.1公顷,三种蔬菜种植的总面积是( )公顷。
12.“校园手机”现象越来越受到社会的关注。“五一”期间,实验小学小记者随机调查了定州市市区若干名学生和家长对小学生在校期间带手机现象的看法,统计整理并制作统计图如下:
(1)这次调查的家长人数是( )人。
(2)补全图1中的条形统计图。
(3)家长赞成学生在校期间带手机的人数占参与调查的家长人数的( )%。
(4)对“在校期间学生带手机”的现象,你有什么看法?说明自己的理由。
三、判断题
13.要清楚表示整体与部分之间的关系,使用扇形统计图更合适。( )
14.某小学学生用手机查资料的人数占69.4%,玩游戏的占51.2%,这些统计数据可以用扇形统计图表示。( )
15.扇形统计图中的各部分占总体的百分比之和为1。( )
16.折线统计图能清楚表示出数量增减变化情况,扇形统计图能清楚表示出各部分同总数之间的关系。( )
17.一个鸡蛋按质量计算,蛋壳、蛋白、蛋黄约占整个鸡蛋的百分比分别为:15%、53%、32%,如果将数据画成统计图,选折线统计图比较合适。( )
四、解答题
18.寻乌城区绿化队去年植柳树、杨树、松树的棵数情况如下图所示:
(1)植柳树的棵数占总棵数的( )%。
(2)如果植松树90棵,那么植杨树多少棵?
19.下图是六(1)班学生关于“最喜欢的球类项目”统计图。
(1)统计图中所有百分比之和是多少?
(2)超过全班人数的学生喜欢的球类项目是什么?写出理由。
(3)如果你是六(1)班的体育委员,班里要组织球类比赛,你打算组织什么比赛,写出理由。
(4)请提出一个数学问题并解答。
20.下面两个图反映的是六年级全体学生参加各种体育活动的情况。
(1)六年级一共有多少人参加体育活动?
(2)六年级踢足球的有多少人?
(3)踢足球的比打篮球的少百分之几?
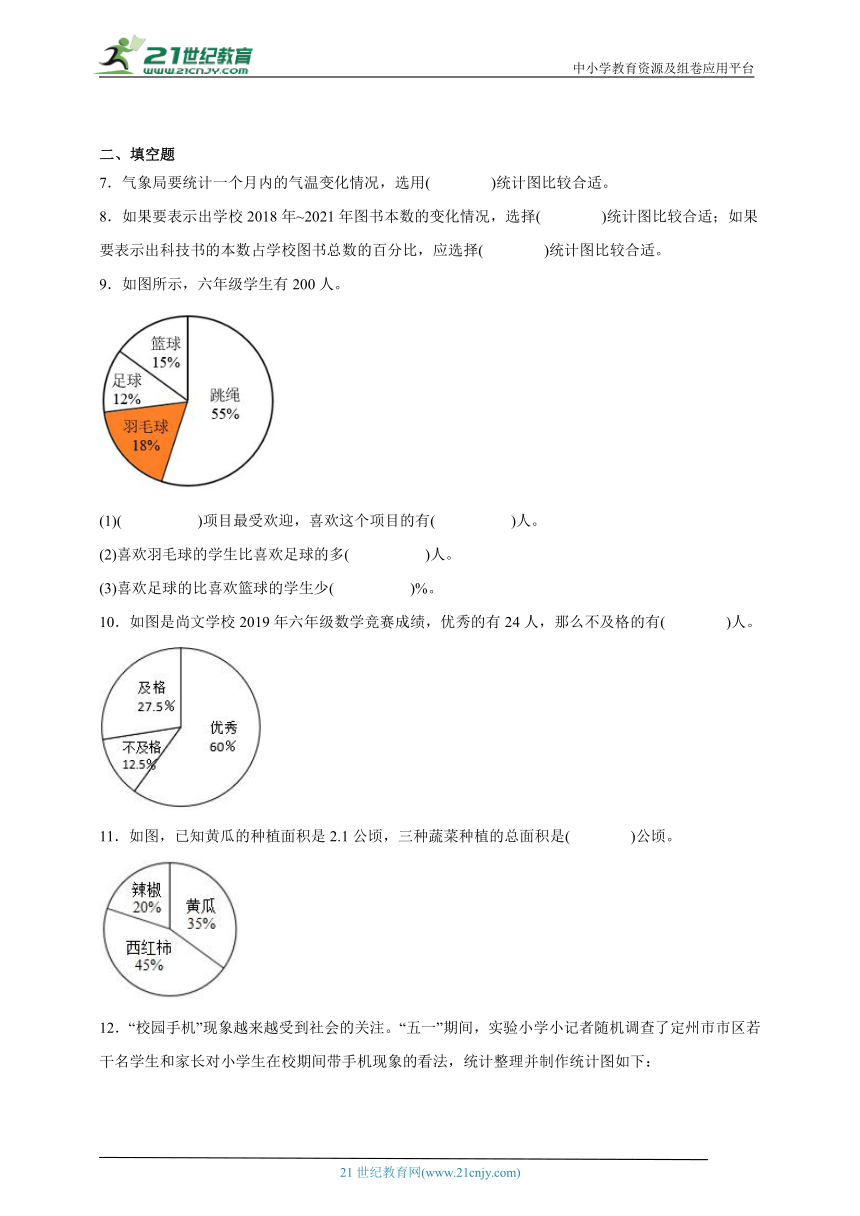
21.在“2020年打击电信网络诈骗犯罪曙光行动”中,我国有23个部门和单位联手打击显成效。学校开展了“防止电信网络诈骗“的调查活动。同学们将调查结果整理分析后,正在绘制统计图。
(1)学校共调查了( )人。
(2)完成如图的两幅统计图,并写出有关的计算过程。
(3)防止网络诈骗,你想对你身边的人说些什么?
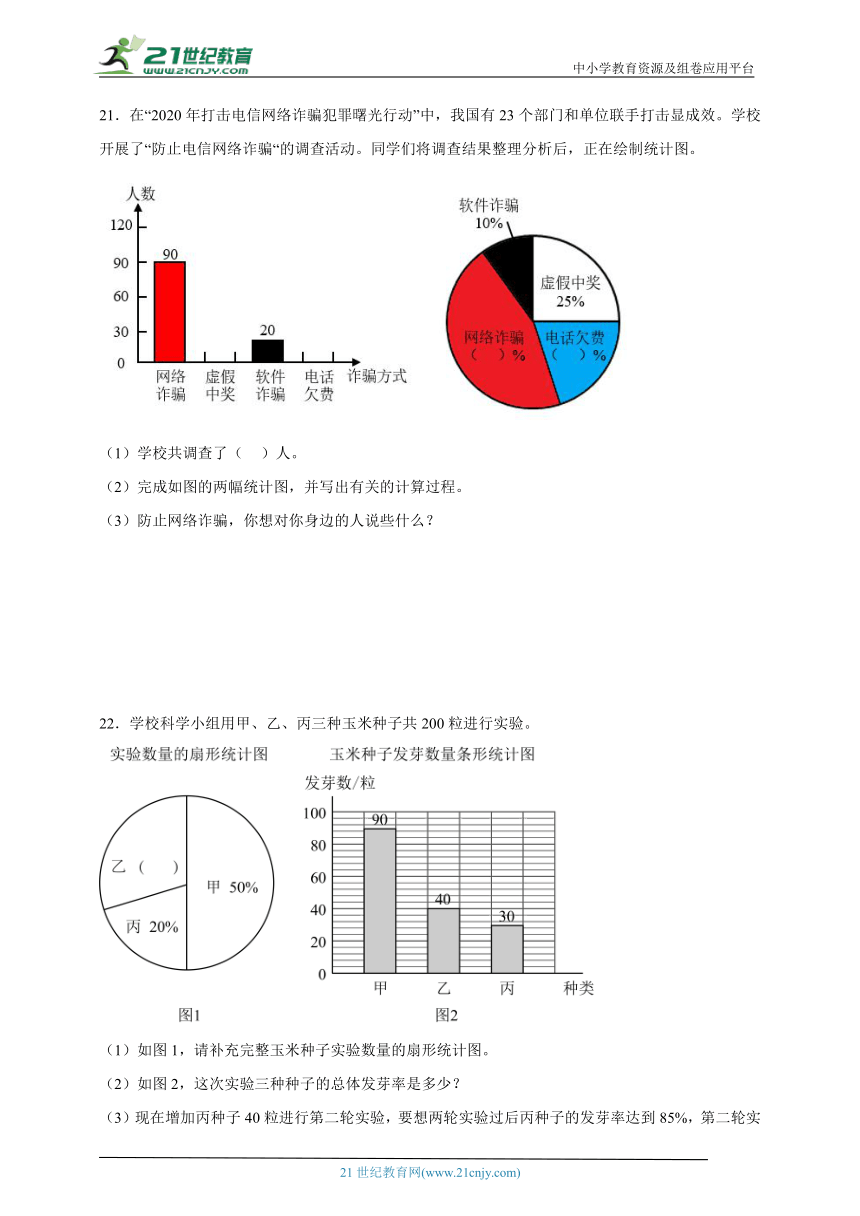
22.学校科学小组用甲、乙、丙三种玉米种子共200粒进行实验。
(1)如图1,请补充完整玉米种子实验数量的扇形统计图。
(2)如图2,这次实验三种种子的总体发芽率是多少?
(3)现在增加丙种子40粒进行第二轮实验,要想两轮实验过后丙种子的发芽率达到85%,第二轮实验的丙种子需要有多少粒发芽?
23.受疫情的影响,越来越多的人选择网上购物,线上经济发展迅速。下面是“双十一”这天天猫某电商对A、B、C三种品牌手机线上销售情况统计绘制的统计图。请根据图中信息解答下列问题。
(1)把图2的扇形统计图补充完整。
(2)列式计算出A品牌和B品牌各销售收入多少万元,并将图1补充完整。
参考答案:
1.D
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;统计表和统计图的区别:统计表反映的数据准确且容易查找;统计图很直观地表示出变化的情况。统计表是统计图的基础。要做统计图,一般会先做统计表。统计表中的数据很详细,但是不利于直观地分析问题。据此解答。
【详解】根据分析得,能更清楚地看出数量增减变化情况的是折线统计图。
故答案为:D
【点睛】此题主要考查统计图表的综合分析、解释与应用。
2.B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】医院统计某位病人一天的体温情况,选用折线统计图更合适。
故答案为:B
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
3.B
【分析】把太阳的总成分看作单位“1”,根据扇形统计图的特点及作用,用整个圆面积表示太阳的总成分,其中氢占75%,氦占25%,据此选择即可。
【详解】A.中氦的百分比比氢的大,不符合题意;
B.中氢占75%、氦占25%,符合题意;
C.中氦占75%、氢占25%,不符合题意;
D.中氢的百分比大于氦,但是氢的百分比不是75%,不符合题意。
故答案为:B
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
4.D
【分析】用数学小组的人数除以数学小组占总人数的百分率即可求出总人数,然后用总人数乘美术小组占的百分率即可求出美术小组的人数。
【详解】27÷54%=50(人)
50×(1-54%-30%)
=50×16%
=8(人)
故答案为D。
5.A
【分析】把全班人数看作单位“1”,用三好学生人数、优秀学生干部人数分别除以全班人数,求出三好学生人数、优秀学生干部人数分别占全班人数的几分之几;
已知圆的圆心角是360°,根据求一个数的几分之几是多少,用360°分别乘三好学生人数、优秀学生干部人数占的分率,即可得解。
【详解】10÷50=
5÷50=
360°×=72°
360°×=36°
在扇形统计图上表示三好学生的圆心角是72°,表示优秀学生干部人数的圆心角是36°。
故答案为:A
【点睛】先求出三好学生人数、优秀学生干部人数分别占的分率,然后根据圆的圆心角为360°,用分数乘法的意义解答。
6.A
【详解】1﹣40%﹣35%﹣15%=10%,
答:D等级所占的百分比是10%.
故选A.
7.折线
【分析】条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;扇形统计图可以清楚地看出各部分数量与总数量之间,部分数量与部分数量之间的关系,据此解答。
【详解】分析可知,气象局要统计一个月内的气温变化情况,选用折线统计图比较合适。
【点睛】本题主要考查统计图的选择,掌握各统计图的特点及作用是解答题目的关键。
8. 折线 扇形
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】如果要表示出学校2018年~2021年图书本数的变化情况,选择折线统计图比较合适;如果要表示出科技书的本数占学校图书总数的百分比,应选择扇形统计图比较合适。
【点睛】此题根据扇形统计图、折线统计图、条形统计图各自的特点来判断。
9.(1) 跳绳 110
(2)12
(3)20
【分析】(1)扇形统计图是以一个圆的面积(看作单位“1”)表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数的统计图。比较各个项目的人数占总人数的百分比的大小,即可求出哪一个项目最受欢迎,并用总人数乘这个项目占总人数的百分比,即可得解。
(2)求一个数的百分之几是多少,用乘法,用总人数乘喜欢羽毛球的学生人数占总人数的百分比,求出喜欢羽毛球的学生人数,同理,用总人数乘喜欢足球的学生人数占总人数的百分比,求出喜欢足球的学生人数,再用喜欢羽毛球的学生人数减去喜欢足球的学生人数,即可得解。
(3)同上,根据求一个数的百分之几是多少,用乘法分别求出喜欢足球的学生人数和喜欢篮球的学生人数,再用喜欢篮球的学生人数减去喜欢足球的学生人数,求出喜欢足球的比喜欢篮球的少的学生人数,再除以喜欢篮球的学生人数,即可得解。
【详解】(1)12%<15%<18%<55%
200×55%=110(人)
即跳绳项目最受欢迎,喜欢这个项目的有110人。
(2)200×18%-200×12%
=36-24
=12(人)
即喜欢羽毛球的学生比喜欢足球的多12人。
(3)200×15%=30(人)
200×12%=24(人)
(30-24)÷30
=6÷30
=0.2
=20%
即喜欢足球的比喜欢篮球的学生少20%。
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
10.5
【分析】根据题意可知,“总人数×60%=24”,据此求出总人数,再乘不及格的人数占总人数的百分比即可。
【详解】24÷60%×12.5%
=40×12.5%
=5(人)
【点睛】熟练掌握百分数乘除法的意义是解答本题的关键。
11.6
【分析】将总面积看作单位“1”,黄瓜种植面积÷对应百分率=总面积。
【详解】2.1÷35%
=2.1÷0.35
=6(公顷)
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
12.(1)400
(2)见详解
(3)10%
(4)我认为不应该带手机,会影响在学校的学习状态,导致学习成绩下降。(答案不唯一,合理即可)
【分析】(1)根据条形统计图可以知道持有无所谓态度的家长有80人,在扇形统计图中持有无所谓态度的家长占20%,所以参与调查的家长人数应该是80÷20%;
(2)已经知道赞成的家长人数是40人,无所谓的家长是80人,所以反对的家长人数应该是(400-40-80)人;
(3)赞成的家长人数是40人,参与调查的人数是400人,所以赞成的家长人数占参与调查的总人数的40÷400=10%;
(4)对“在校期间学生带手机”的现象,我认为不应该带手机,会影响在学校的学习状态,导致学习成绩下降。(答案不唯一,合理即可)
【详解】(1)80÷20%=400(人)
(2)
(3)40÷400=10%
(4)我认为不应该带手机,会影响在学校的学习状态,导致学习成绩下降。(答案不唯一,合理即可)
【点睛】考查条形统计图与扇形统计图的相关知识,重点是能够正确的进行数据分析。
13.√
【分析】条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系,据此判断即可。
【详解】根据各统计图的特征可知:要清楚表示整体与部分之间的关系,使用扇形统计图更合适,说法正确。
故答案为:√
【点睛】掌握不同的统计图表的特征选用合适的统计图是解题的关键。
14.×
【分析】扇形统计图中用整个圆表示总数量,圆内各个扇形的大小表示各部分数量占总数量的百分比,通过扇形统计图可以清楚地看出各部分数量与总数量之间,各项的百分比之和不能超过100%,据此解答。
【详解】69.4%+51.2%=120.6%
因为120.6%>100%,也就是说被调查的学生中,有同时选择两项或两项以上的,所以不能用扇形统计图表示某小学学生用手机查资料的人数和玩游戏的人数占总人数的百分率。
故答案为:×
【点睛】掌握扇形统计图的特点及作用是解答题目的关键。
15.√
【分析】根据扇形统计图的特点及作用,扇形统计图能够表示部分与整体之间的关系,也就是用整个圆表示总体,用扇形表示各部分占总体的百分比,各部分占总体的百分比之和为1。据此解答。
【详解】据分析可知:扇形统计图中的各部分占总体的百分比之和为1。此说法正确。
故答案为:√
【点睛】本题考查的是扇形统计图的定义。在扇形统计图中,各部分占总体的百分比之和为1,每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与360°的比。
16.√
【详解】如图:
折线统计图能清楚表示出数量增减变化情况,扇形统计图能清楚表示出各部分同总数之间的关系。
原题说法正确。
故答案为:√
17.×
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】由分析可知:
一个鸡蛋按质量计算,蛋壳、蛋白、蛋黄约占整个鸡蛋的百分比分别为:15%、53%、32%,如果将数据画成统计图,选扇形统计图比较合适。原题干说法错误。
故答案为:×
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
18.(1)40
(2)270棵
【分析】(1)用100%减去植杨树和松树的百分比,求出植柳树的棵数占总棵数的百分之几;
(2)用松树90棵除以它的占比15%,先求出总的植树数,再将总的植树数乘45%,求出杨树的数量即可。
【详解】(1)100%―45%―15%=40%,所以植柳树的棵数占总棵数的40%;
(2)90÷15%×45%
=600×45%
=270(棵)
答:植杨树270棵。
【点睛】本题考查了扇形统计图,它用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数。通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系。
19.(1)1;
(2)篮球
(3)我打算组织篮球比赛,因为喜欢篮球的人数最多。
(4)喜欢足球人数比喜欢篮球人数少百分之几;25%。
【分析】根据扇形统计图提供的信息解答即可。
【详解】(1)10%+30%+15%+5%+40%=1
答:统计图中所有百分比之和是1。
(2)40%=
答:超过全班人数的学生喜欢的球类项目是篮球。
(3)我打算组织篮球比赛,因为喜欢篮球的人数最多。
(4)喜欢足球人数比喜欢篮球人数少百分之几?
(40%-30%)÷40%
=10%÷40%
=25%
答:喜欢足球人数比喜欢篮球人数少25%。
【点睛】本题考查扇形统计图,解答本题的关键是掌握扇形统计图的特征。
20.(1)200人;(2)40人;(3)50%
【分析】(1)由图可知,玩乒乓球的有20人,占六年级参加体育活动人数的10%。据此,利用除法求出六年级参加体育活动的总人数即可。
(2)用总人数减去参加篮球、乒乓球和其他的人数,得到踢足球的人数。
(3)先计算出踢足球的比打篮球的少多少人,再利用除法求出少百分之几。
【详解】(1)20÷10%=200(人)
(2)200-20-60-80
=180-60-80
=120-80
=40(人)
(3)(80-40)÷80×100%
=40÷80×100%
=0.5×100%
=50%
答:六年级一共有200人参加体育活动;六年级踢足球的有40人;踢足球的比打篮球的少50%。
【点睛】本题考查了条形统计图和扇形统计图,能够从图中获取有用信息是解题的关键。
21.(1)200
(2)见详解
(3)见详解
【分析】(1)把调查的总人数看作单位“1”,由两幅统计图可知,软件诈骗的人数是20人,占调查总人数的10%,根据已知一个数的百分之几是多少,求这个数,用除法求出总人数。
(2)分别求出虚假中奖和电话欠费的人数,以及电话欠费和网络诈骗的百分比,然后把两幅统计图补充完整。
(3)提出建议,合理即可。
【详解】(1)20÷10%
=20÷0.1
=200(人)
学校共调查了200人。
(2)虚假中奖人数:
200×25%
=200×0.25
=50(人)
电话欠费人数:200-90-50-20=40(人)
电话欠费分率:
40÷200×100%
=0.2×100%
=20%
网络诈骗分率:1-10%-25%-20%=45%
如图:
(3)为了防止微信诈骗,我想对身边的人说:加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电,关注国家反诈平台,加强自我道德建设,克服“贪小便宜”、“不劳而获”的思想等。(答案不唯一)
【点睛】本题考查条形统计图与扇形统计图的综合应用,根据统计图提供的信息解决有关的实际问题。
22.(1)见详解
(2)80%
(3)38粒
【分析】(1)把甲、乙、丙三种玉米种子的总粒数看作单位“1”,用单位“1”减去甲、丙占总粒数的百分率即可求出乙种玉米种子占总粒数的百分率;
(2)根据发芽率=发芽的种子的粒数÷总粒数×100%,据此解答即可;
(3)根据求一个数的百分之几是多少,用乘法求出丙种子原来的粒数,再加上40粒就是第二轮实验时丙种子的粒数,再根据发芽的粒数=种子的总粒数×发芽率,据此求出发芽的种子的粒数,最后再减去第一轮丙种子发芽的粒数即可。
【详解】(1)1-50%-20%
=50%-20%
=30%
如图所示:
(2)(90+40+30)÷200×100%
=160÷200×100%
=0.8×100%
=80%
答:这次实验三种种子的总体发芽率是80%。
(3)(200×20%+40)×85%
=(40+40)×85%
=80×85%
=68(粒)
68-30=38(粒)
答:第二轮实验的丙种子需要有38粒发芽。
【点睛】本题考查发芽率,明确发芽率的计算方法是解题的关键。
23.(1)见详解
(2)600万元、900万元;作图见详解
【分析】(1)将销售总量看作单位“1”,1-B品牌对应百分率-C品牌对应百分率=A品牌对应百分率,据此作图;
(2)C品牌销售金额÷对应百分率=销售总金额,总销售金额分别乘A品牌和B品牌对应百分率,分别求出两种品牌销售金额,作图即可。
【详解】(1)1-30%-50%=20%
(2)1500÷50%=3000(万元)
3000×20%==600(万元)
3000×30%=900(万元)
答:A品牌和B品牌各销售收入600万元、900万元。
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1单元扇形统计图高频考点检测卷-数学六年级下册苏教版
一、选择题
1.能更清楚地看出数量增减变化情况的是( )。
A.单式统计表 B.复式统计表 C.条形统计图 D.折线统计图
2.医院统计某位病人一天的体温情况,选用( )统计图更合适。
A.扇形 B.折线 C.条形 D.都可以
3.太阳是由75%的氢和25%的氦组成的,下面( )统计图能正确表达这个信息。
A. B. C. D.
4.如图所示,初一(2)班的参加数学兴趣小组的有27人,那么参加美术小组的有( )人。
A.18 B.50 C.15 D.8
5.某班有50人,其中三好学生10人,优秀学生干部5人,在扇形统计图上表示三好学生和优秀学生干部人数的圆心角分别是( )。
A.72°,36° B.100°,50° C.80°,40° D.120°,60°
6.学校将某一年级数学考试成绩分为A、B、C、D四个等级,绘制成扇形统计图,则D等级所占的百分比是( )
A.10% B.5% C.20% D.8%
二、填空题
7.气象局要统计一个月内的气温变化情况,选用( )统计图比较合适。
8.如果要表示出学校2018年~2021年图书本数的变化情况,选择( )统计图比较合适;如果要表示出科技书的本数占学校图书总数的百分比,应选择( )统计图比较合适。
9.如图所示,六年级学生有200人。
(1)( )项目最受欢迎,喜欢这个项目的有( )人。
(2)喜欢羽毛球的学生比喜欢足球的多( )人。
(3)喜欢足球的比喜欢篮球的学生少( )%。
10.如图是尚文学校2019年六年级数学竞赛成绩,优秀的有24人,那么不及格的有( )人。
11.如图,已知黄瓜的种植面积是2.1公顷,三种蔬菜种植的总面积是( )公顷。
12.“校园手机”现象越来越受到社会的关注。“五一”期间,实验小学小记者随机调查了定州市市区若干名学生和家长对小学生在校期间带手机现象的看法,统计整理并制作统计图如下:
(1)这次调查的家长人数是( )人。
(2)补全图1中的条形统计图。
(3)家长赞成学生在校期间带手机的人数占参与调查的家长人数的( )%。
(4)对“在校期间学生带手机”的现象,你有什么看法?说明自己的理由。
三、判断题
13.要清楚表示整体与部分之间的关系,使用扇形统计图更合适。( )
14.某小学学生用手机查资料的人数占69.4%,玩游戏的占51.2%,这些统计数据可以用扇形统计图表示。( )
15.扇形统计图中的各部分占总体的百分比之和为1。( )
16.折线统计图能清楚表示出数量增减变化情况,扇形统计图能清楚表示出各部分同总数之间的关系。( )
17.一个鸡蛋按质量计算,蛋壳、蛋白、蛋黄约占整个鸡蛋的百分比分别为:15%、53%、32%,如果将数据画成统计图,选折线统计图比较合适。( )
四、解答题
18.寻乌城区绿化队去年植柳树、杨树、松树的棵数情况如下图所示:
(1)植柳树的棵数占总棵数的( )%。
(2)如果植松树90棵,那么植杨树多少棵?
19.下图是六(1)班学生关于“最喜欢的球类项目”统计图。
(1)统计图中所有百分比之和是多少?
(2)超过全班人数的学生喜欢的球类项目是什么?写出理由。
(3)如果你是六(1)班的体育委员,班里要组织球类比赛,你打算组织什么比赛,写出理由。
(4)请提出一个数学问题并解答。
20.下面两个图反映的是六年级全体学生参加各种体育活动的情况。
(1)六年级一共有多少人参加体育活动?
(2)六年级踢足球的有多少人?
(3)踢足球的比打篮球的少百分之几?
21.在“2020年打击电信网络诈骗犯罪曙光行动”中,我国有23个部门和单位联手打击显成效。学校开展了“防止电信网络诈骗“的调查活动。同学们将调查结果整理分析后,正在绘制统计图。
(1)学校共调查了( )人。
(2)完成如图的两幅统计图,并写出有关的计算过程。
(3)防止网络诈骗,你想对你身边的人说些什么?
22.学校科学小组用甲、乙、丙三种玉米种子共200粒进行实验。
(1)如图1,请补充完整玉米种子实验数量的扇形统计图。
(2)如图2,这次实验三种种子的总体发芽率是多少?
(3)现在增加丙种子40粒进行第二轮实验,要想两轮实验过后丙种子的发芽率达到85%,第二轮实验的丙种子需要有多少粒发芽?
23.受疫情的影响,越来越多的人选择网上购物,线上经济发展迅速。下面是“双十一”这天天猫某电商对A、B、C三种品牌手机线上销售情况统计绘制的统计图。请根据图中信息解答下列问题。
(1)把图2的扇形统计图补充完整。
(2)列式计算出A品牌和B品牌各销售收入多少万元,并将图1补充完整。
参考答案:
1.D
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;统计表和统计图的区别:统计表反映的数据准确且容易查找;统计图很直观地表示出变化的情况。统计表是统计图的基础。要做统计图,一般会先做统计表。统计表中的数据很详细,但是不利于直观地分析问题。据此解答。
【详解】根据分析得,能更清楚地看出数量增减变化情况的是折线统计图。
故答案为:D
【点睛】此题主要考查统计图表的综合分析、解释与应用。
2.B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】医院统计某位病人一天的体温情况,选用折线统计图更合适。
故答案为:B
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
3.B
【分析】把太阳的总成分看作单位“1”,根据扇形统计图的特点及作用,用整个圆面积表示太阳的总成分,其中氢占75%,氦占25%,据此选择即可。
【详解】A.中氦的百分比比氢的大,不符合题意;
B.中氢占75%、氦占25%,符合题意;
C.中氦占75%、氢占25%,不符合题意;
D.中氢的百分比大于氦,但是氢的百分比不是75%,不符合题意。
故答案为:B
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
4.D
【分析】用数学小组的人数除以数学小组占总人数的百分率即可求出总人数,然后用总人数乘美术小组占的百分率即可求出美术小组的人数。
【详解】27÷54%=50(人)
50×(1-54%-30%)
=50×16%
=8(人)
故答案为D。
5.A
【分析】把全班人数看作单位“1”,用三好学生人数、优秀学生干部人数分别除以全班人数,求出三好学生人数、优秀学生干部人数分别占全班人数的几分之几;
已知圆的圆心角是360°,根据求一个数的几分之几是多少,用360°分别乘三好学生人数、优秀学生干部人数占的分率,即可得解。
【详解】10÷50=
5÷50=
360°×=72°
360°×=36°
在扇形统计图上表示三好学生的圆心角是72°,表示优秀学生干部人数的圆心角是36°。
故答案为:A
【点睛】先求出三好学生人数、优秀学生干部人数分别占的分率,然后根据圆的圆心角为360°,用分数乘法的意义解答。
6.A
【详解】1﹣40%﹣35%﹣15%=10%,
答:D等级所占的百分比是10%.
故选A.
7.折线
【分析】条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;扇形统计图可以清楚地看出各部分数量与总数量之间,部分数量与部分数量之间的关系,据此解答。
【详解】分析可知,气象局要统计一个月内的气温变化情况,选用折线统计图比较合适。
【点睛】本题主要考查统计图的选择,掌握各统计图的特点及作用是解答题目的关键。
8. 折线 扇形
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】如果要表示出学校2018年~2021年图书本数的变化情况,选择折线统计图比较合适;如果要表示出科技书的本数占学校图书总数的百分比,应选择扇形统计图比较合适。
【点睛】此题根据扇形统计图、折线统计图、条形统计图各自的特点来判断。
9.(1) 跳绳 110
(2)12
(3)20
【分析】(1)扇形统计图是以一个圆的面积(看作单位“1”)表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数的统计图。比较各个项目的人数占总人数的百分比的大小,即可求出哪一个项目最受欢迎,并用总人数乘这个项目占总人数的百分比,即可得解。
(2)求一个数的百分之几是多少,用乘法,用总人数乘喜欢羽毛球的学生人数占总人数的百分比,求出喜欢羽毛球的学生人数,同理,用总人数乘喜欢足球的学生人数占总人数的百分比,求出喜欢足球的学生人数,再用喜欢羽毛球的学生人数减去喜欢足球的学生人数,即可得解。
(3)同上,根据求一个数的百分之几是多少,用乘法分别求出喜欢足球的学生人数和喜欢篮球的学生人数,再用喜欢篮球的学生人数减去喜欢足球的学生人数,求出喜欢足球的比喜欢篮球的少的学生人数,再除以喜欢篮球的学生人数,即可得解。
【详解】(1)12%<15%<18%<55%
200×55%=110(人)
即跳绳项目最受欢迎,喜欢这个项目的有110人。
(2)200×18%-200×12%
=36-24
=12(人)
即喜欢羽毛球的学生比喜欢足球的多12人。
(3)200×15%=30(人)
200×12%=24(人)
(30-24)÷30
=6÷30
=0.2
=20%
即喜欢足球的比喜欢篮球的学生少20%。
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
10.5
【分析】根据题意可知,“总人数×60%=24”,据此求出总人数,再乘不及格的人数占总人数的百分比即可。
【详解】24÷60%×12.5%
=40×12.5%
=5(人)
【点睛】熟练掌握百分数乘除法的意义是解答本题的关键。
11.6
【分析】将总面积看作单位“1”,黄瓜种植面积÷对应百分率=总面积。
【详解】2.1÷35%
=2.1÷0.35
=6(公顷)
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
12.(1)400
(2)见详解
(3)10%
(4)我认为不应该带手机,会影响在学校的学习状态,导致学习成绩下降。(答案不唯一,合理即可)
【分析】(1)根据条形统计图可以知道持有无所谓态度的家长有80人,在扇形统计图中持有无所谓态度的家长占20%,所以参与调查的家长人数应该是80÷20%;
(2)已经知道赞成的家长人数是40人,无所谓的家长是80人,所以反对的家长人数应该是(400-40-80)人;
(3)赞成的家长人数是40人,参与调查的人数是400人,所以赞成的家长人数占参与调查的总人数的40÷400=10%;
(4)对“在校期间学生带手机”的现象,我认为不应该带手机,会影响在学校的学习状态,导致学习成绩下降。(答案不唯一,合理即可)
【详解】(1)80÷20%=400(人)
(2)
(3)40÷400=10%
(4)我认为不应该带手机,会影响在学校的学习状态,导致学习成绩下降。(答案不唯一,合理即可)
【点睛】考查条形统计图与扇形统计图的相关知识,重点是能够正确的进行数据分析。
13.√
【分析】条形统计图用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系,据此判断即可。
【详解】根据各统计图的特征可知:要清楚表示整体与部分之间的关系,使用扇形统计图更合适,说法正确。
故答案为:√
【点睛】掌握不同的统计图表的特征选用合适的统计图是解题的关键。
14.×
【分析】扇形统计图中用整个圆表示总数量,圆内各个扇形的大小表示各部分数量占总数量的百分比,通过扇形统计图可以清楚地看出各部分数量与总数量之间,各项的百分比之和不能超过100%,据此解答。
【详解】69.4%+51.2%=120.6%
因为120.6%>100%,也就是说被调查的学生中,有同时选择两项或两项以上的,所以不能用扇形统计图表示某小学学生用手机查资料的人数和玩游戏的人数占总人数的百分率。
故答案为:×
【点睛】掌握扇形统计图的特点及作用是解答题目的关键。
15.√
【分析】根据扇形统计图的特点及作用,扇形统计图能够表示部分与整体之间的关系,也就是用整个圆表示总体,用扇形表示各部分占总体的百分比,各部分占总体的百分比之和为1。据此解答。
【详解】据分析可知:扇形统计图中的各部分占总体的百分比之和为1。此说法正确。
故答案为:√
【点睛】本题考查的是扇形统计图的定义。在扇形统计图中,各部分占总体的百分比之和为1,每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与360°的比。
16.√
【详解】如图:
折线统计图能清楚表示出数量增减变化情况,扇形统计图能清楚表示出各部分同总数之间的关系。
原题说法正确。
故答案为:√
17.×
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】由分析可知:
一个鸡蛋按质量计算,蛋壳、蛋白、蛋黄约占整个鸡蛋的百分比分别为:15%、53%、32%,如果将数据画成统计图,选扇形统计图比较合适。原题干说法错误。
故答案为:×
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
18.(1)40
(2)270棵
【分析】(1)用100%减去植杨树和松树的百分比,求出植柳树的棵数占总棵数的百分之几;
(2)用松树90棵除以它的占比15%,先求出总的植树数,再将总的植树数乘45%,求出杨树的数量即可。
【详解】(1)100%―45%―15%=40%,所以植柳树的棵数占总棵数的40%;
(2)90÷15%×45%
=600×45%
=270(棵)
答:植杨树270棵。
【点睛】本题考查了扇形统计图,它用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数。通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系。
19.(1)1;
(2)篮球
(3)我打算组织篮球比赛,因为喜欢篮球的人数最多。
(4)喜欢足球人数比喜欢篮球人数少百分之几;25%。
【分析】根据扇形统计图提供的信息解答即可。
【详解】(1)10%+30%+15%+5%+40%=1
答:统计图中所有百分比之和是1。
(2)40%=
答:超过全班人数的学生喜欢的球类项目是篮球。
(3)我打算组织篮球比赛,因为喜欢篮球的人数最多。
(4)喜欢足球人数比喜欢篮球人数少百分之几?
(40%-30%)÷40%
=10%÷40%
=25%
答:喜欢足球人数比喜欢篮球人数少25%。
【点睛】本题考查扇形统计图,解答本题的关键是掌握扇形统计图的特征。
20.(1)200人;(2)40人;(3)50%
【分析】(1)由图可知,玩乒乓球的有20人,占六年级参加体育活动人数的10%。据此,利用除法求出六年级参加体育活动的总人数即可。
(2)用总人数减去参加篮球、乒乓球和其他的人数,得到踢足球的人数。
(3)先计算出踢足球的比打篮球的少多少人,再利用除法求出少百分之几。
【详解】(1)20÷10%=200(人)
(2)200-20-60-80
=180-60-80
=120-80
=40(人)
(3)(80-40)÷80×100%
=40÷80×100%
=0.5×100%
=50%
答:六年级一共有200人参加体育活动;六年级踢足球的有40人;踢足球的比打篮球的少50%。
【点睛】本题考查了条形统计图和扇形统计图,能够从图中获取有用信息是解题的关键。
21.(1)200
(2)见详解
(3)见详解
【分析】(1)把调查的总人数看作单位“1”,由两幅统计图可知,软件诈骗的人数是20人,占调查总人数的10%,根据已知一个数的百分之几是多少,求这个数,用除法求出总人数。
(2)分别求出虚假中奖和电话欠费的人数,以及电话欠费和网络诈骗的百分比,然后把两幅统计图补充完整。
(3)提出建议,合理即可。
【详解】(1)20÷10%
=20÷0.1
=200(人)
学校共调查了200人。
(2)虚假中奖人数:
200×25%
=200×0.25
=50(人)
电话欠费人数:200-90-50-20=40(人)
电话欠费分率:
40÷200×100%
=0.2×100%
=20%
网络诈骗分率:1-10%-25%-20%=45%
如图:
(3)为了防止微信诈骗,我想对身边的人说:加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电,关注国家反诈平台,加强自我道德建设,克服“贪小便宜”、“不劳而获”的思想等。(答案不唯一)
【点睛】本题考查条形统计图与扇形统计图的综合应用,根据统计图提供的信息解决有关的实际问题。
22.(1)见详解
(2)80%
(3)38粒
【分析】(1)把甲、乙、丙三种玉米种子的总粒数看作单位“1”,用单位“1”减去甲、丙占总粒数的百分率即可求出乙种玉米种子占总粒数的百分率;
(2)根据发芽率=发芽的种子的粒数÷总粒数×100%,据此解答即可;
(3)根据求一个数的百分之几是多少,用乘法求出丙种子原来的粒数,再加上40粒就是第二轮实验时丙种子的粒数,再根据发芽的粒数=种子的总粒数×发芽率,据此求出发芽的种子的粒数,最后再减去第一轮丙种子发芽的粒数即可。
【详解】(1)1-50%-20%
=50%-20%
=30%
如图所示:
(2)(90+40+30)÷200×100%
=160÷200×100%
=0.8×100%
=80%
答:这次实验三种种子的总体发芽率是80%。
(3)(200×20%+40)×85%
=(40+40)×85%
=80×85%
=68(粒)
68-30=38(粒)
答:第二轮实验的丙种子需要有38粒发芽。
【点睛】本题考查发芽率,明确发芽率的计算方法是解题的关键。
23.(1)见详解
(2)600万元、900万元;作图见详解
【分析】(1)将销售总量看作单位“1”,1-B品牌对应百分率-C品牌对应百分率=A品牌对应百分率,据此作图;
(2)C品牌销售金额÷对应百分率=销售总金额,总销售金额分别乘A品牌和B品牌对应百分率,分别求出两种品牌销售金额,作图即可。
【详解】(1)1-30%-50%=20%
(2)1500÷50%=3000(万元)
3000×20%==600(万元)
3000×30%=900(万元)
答:A品牌和B品牌各销售收入600万元、900万元。
【点睛】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数相关解题思路解答即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
