【五环分层导学-课件】3.7第三章单元复习-北师大版数学八(下)
文档属性
| 名称 | 【五环分层导学-课件】3.7第三章单元复习-北师大版数学八(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 23.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 11:48:33 | ||
图片预览







文档简介
(共34张PPT)
第三章
图形的平移与旋转
第7课 单元复习
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】平移是否改变图形的位置、形状和大小?旋转呢?请举例说明.
【问题2】平移、旋转各有哪些基本性质?请举例说明.
【问题3】在平面直角坐标系中,平移后的图形与原图形对应点的坐标之间有怎样的关系?
【问题4】两个成中心对称的图形有哪些特性?中心对称图形有哪些特性?
【问题5】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现本章知识结构.
【例题1】一个图形无论经过平移还是旋转,有以下说法:①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有发生变化.其中都正确的说法是(%////%)
A.①、②、③ B.①、②、④
C.①、③、④ D.②、③、④
D
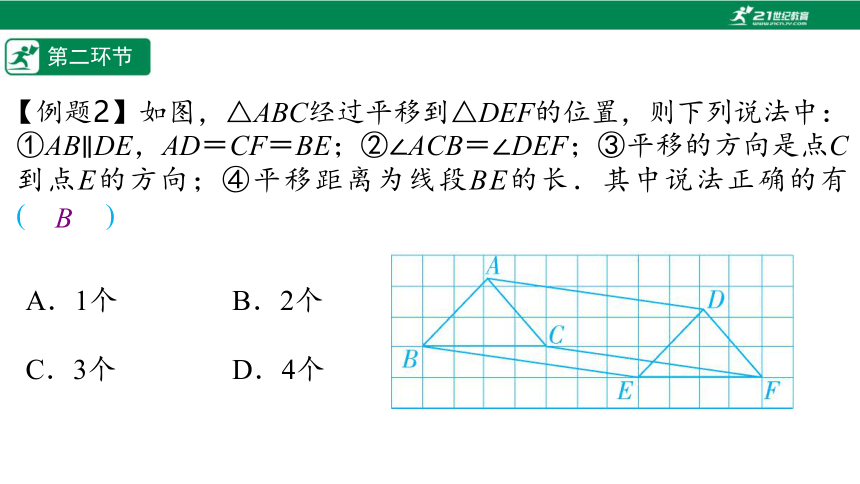
【例题2】如图,△ABC经过平移到△DEF的位置,则下列说法中:①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C到点E的方向;④平移距离为线段BE的长.其中说法正确的有(%////%)
A.1个 B.2个
C.3个 D.4个
B
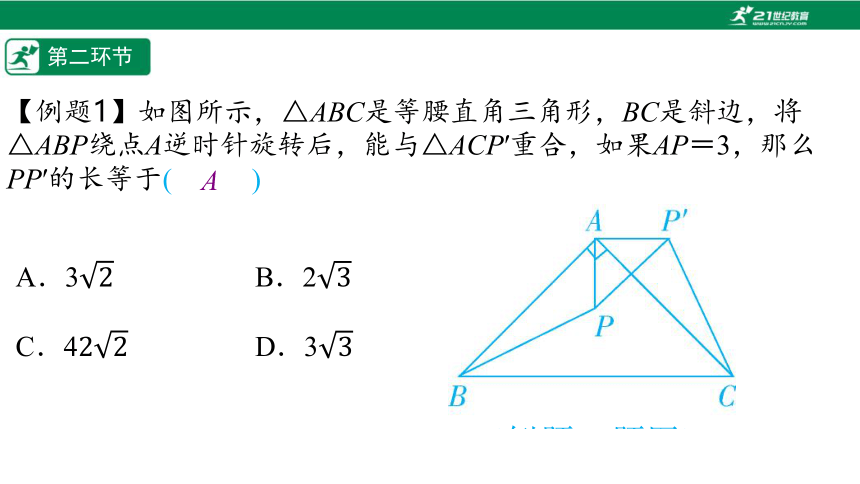
【例题1】如图所示,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′的长等于(%////%)
A.3 B.2
C.4 D.3
A
【例题2】如图,直线y=-x+4与x轴,y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是(%////%)
A.(7,3) B.(4,5)
C.(7,4) D.(3,4)
A
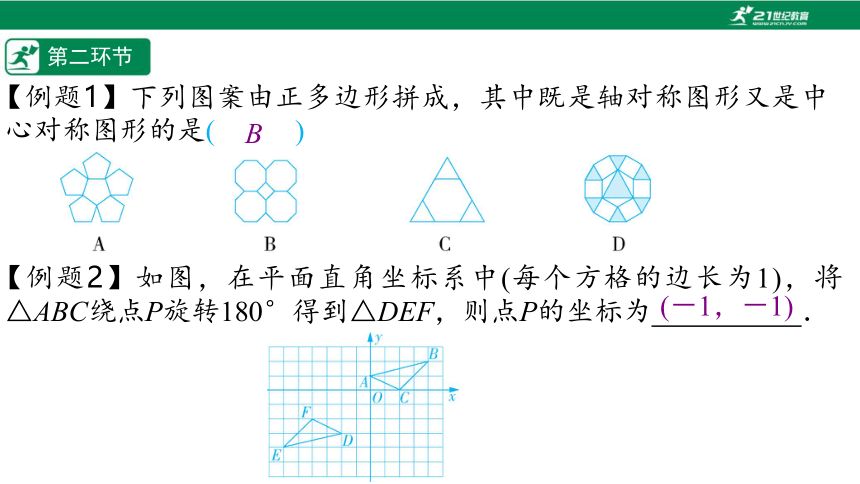
【例题1】下列图案由正多边形拼成,其中既是轴对称图形又是中心对称图形的是(%////%)
【例题2】如图,在平面直角坐标系中(每个方格的边长为1),将△ABC绕点P旋转180°得到△DEF,则点P的坐标为// .
B
/(-1,-1)
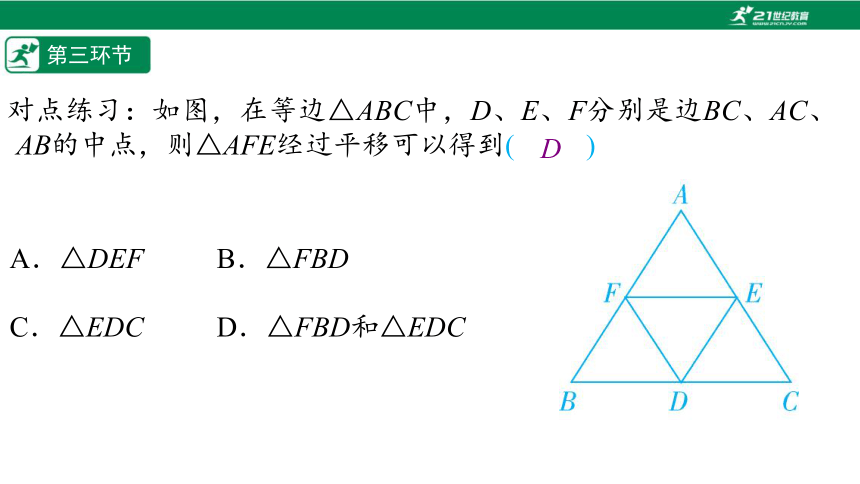
对点练习:如图,在等边△ABC中,D、E、F分别是边BC、AC、AB的中点,则△AFE经过平移可以得到(%///%)
A.△DEF B.△FBD
C.△EDC D.△FBD和△EDC
D
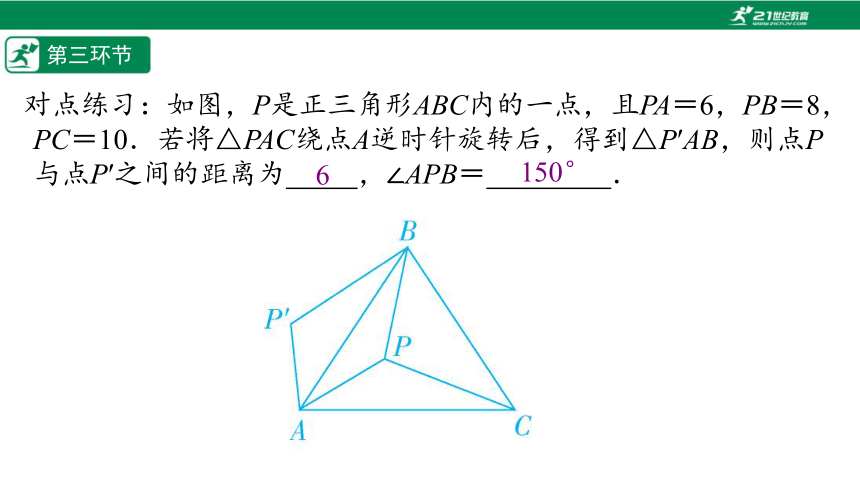
对点练习:如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与点P′之间的距离为%///%,∠APB=%// //%.
6/
150°
对点练习:如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C.设点A的坐标为(a,b),则点A′的坐标为(%////%)
A.(-a,-b) B.(-a,-b-1)
C.(-a,-b+1) D.(-a,-b-2)
D
1.将长度为5 cm的线段向上平移10 cm后,所得线段的长度是(%////%)
A.10 cm B.5 cm
C.0 cm D.无法确定
B
2.以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是(%////%)
B
3.一个图形无论经过平移变换,还是经过旋转变换,下列说法正确的是(%////%)
①对应线段平行;②对应线段相等;③图形的形状和大小都没有发生变化;④对应角相等.
A.①②③ B.②③④
C.①②④ D.①③④
B
4.如图,△ABC和△BDE是等边三角形,点A、B、D在一条直线上,并且AB=BD .由一个三角形变换到另一个三角形(%///%)
A.仅能由平移得到
B.仅能由旋转得到
C.既能由平移得到,也能由旋转得到
D.既不能由平移得到,也不能由旋转得到
C/
5.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是(%////%)
A.(-3,2) B.(-1,2)
C.(1,2) D.(1,-2)
C
6.如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于(%////%)
A.55° B.70°
C.125° D.145°
C
7.如图,若△DEF是由△ABC经过平移后得到的,则平移的距离是(%////%)
A.线段BC的长度
B.线段BE的长度
C.线段EC的长度
D.线段EF的长度
B
8.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=(%////%)
A.30° B.35°
C.40° D.50°
C
9.在平面直角坐标系中,线段OP的两个端点坐标分别是O(0,0),P(4,3),将线段OP绕点O逆时针旋转90°到OP′位置,则点P′的坐标为(%////%)
A.(3,4) B.(-4,3)
C.(-3,4) D.(4,-3)
C
10.如图,△ABO中,AB⊥OB,OB=,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为(%////%)
A.(-1,-)
B.(-1,-)或(-2,0)
C.(-,-1)或(0,-2)
D.(-,-1)
B
11.如图,在四边形ABCD中,AD∥BC,BC>AD,∠B与∠C互余,将AB,CD分别平移到EF和EG的位置,则△EFG为%/// /%三角形.
直角
12.如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=%////%度.
20
13 .如图,在平面直角坐标系中,将线段AB绕点A按逆时针方向旋转90°后,得到线段AB′,则点B′的坐标为//% .
/(4,2)
14.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=%// //%.
20°
15.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C都是格点.
(1)将△ABC向左平移6个单位长度得到得到△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2,请画出△A2B2C2.
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求.
16.如图①,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:如图②,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是%// //%;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是%////%.
DE∥AC
解:(1)由旋转可知:CA=CD,
∵∠ACB=90°,∠B=30°,∴∠CAD=60°,
∴△ADC是等边三角形,∴∠DCA=60°,
∵∠ECD=90°,∠DEC=30°,∴∠CDE=60°,
∴∠EDC=∠DCA,∴DE∥AC,
②∵AB=2AC,AD=AC,∴AD=BD,∴S△BDC=S△ADC,
∵DE∥AC,∴S△ADC=S△ACE,∴S1=S2.
故答案为:DE∥AC,S1=S2.
(2)猜想论证:当△DEC绕点C旋转到如图③所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(2)∵△DEC是由△ABC旋转得到,∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=90°,
∴∠ACN=∠DCM,
在△ACN和△DCM中,,
∴△ACN≌△DCM(AAS),
∴AN=DM,∴S△BDC=S△AEC.
(3)拓展探究:已知∠ABC=60°,点D是角平分线上一点,BD=CD=6,DE∥AB交BC于点E(如图④).若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.
(3)如图中,作DF∥BC交AB于F.延长CD交AB于H.
∵DF∥BE,DE∥BF,∴四边形DEBF是平行四边形,
∴S△BDF=S△BDE,S△BDF=S△DFC,∴S△DFC=S△BDE,
∵∠ABC=60°,BD平分∠ABC,∴∠ABD=∠DBE=30°,
∵DF∥BE,∴∠FBD=∠FDB=30°,∴FB=FD,
∵BD=CD=6,∴∠DBC=∠DCB=30°,
∵∠DEC=∠ABC=60°,∴∠CDE=90°,
∴由勾股定理得DE=2,∴BF=DE=2,
∵DE∥AB,∴∠BHC=∠EDC=90°,
∴CH⊥AB,作点F关于CH的对称点F′,连接DF′,易知S△DFC=S△DF′C,
在Rt△DFH中,HD=BD=3,∴FH=HF′=,∴BF′=4,
综上所述,满足条件的BF的值为2或4.//
17.如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一种实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0).得到正方形A′B′C′D′及其内部的点,其中点A、B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
解:由点A到点A′,可得方程组;
由点B到点B′,可得方程组,
解得,
设F点的坐标为(x,y),点F′与点F重合得到方程组
解得,即F(1,4).
第三章
图形的平移与旋转
第7课 单元复习
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】平移是否改变图形的位置、形状和大小?旋转呢?请举例说明.
【问题2】平移、旋转各有哪些基本性质?请举例说明.
【问题3】在平面直角坐标系中,平移后的图形与原图形对应点的坐标之间有怎样的关系?
【问题4】两个成中心对称的图形有哪些特性?中心对称图形有哪些特性?
【问题5】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现本章知识结构.
【例题1】一个图形无论经过平移还是旋转,有以下说法:①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有发生变化.其中都正确的说法是(%////%)
A.①、②、③ B.①、②、④
C.①、③、④ D.②、③、④
D
【例题2】如图,△ABC经过平移到△DEF的位置,则下列说法中:①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C到点E的方向;④平移距离为线段BE的长.其中说法正确的有(%////%)
A.1个 B.2个
C.3个 D.4个
B
【例题1】如图所示,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′的长等于(%////%)
A.3 B.2
C.4 D.3
A
【例题2】如图,直线y=-x+4与x轴,y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是(%////%)
A.(7,3) B.(4,5)
C.(7,4) D.(3,4)
A
【例题1】下列图案由正多边形拼成,其中既是轴对称图形又是中心对称图形的是(%////%)
【例题2】如图,在平面直角坐标系中(每个方格的边长为1),将△ABC绕点P旋转180°得到△DEF,则点P的坐标为// .
B
/(-1,-1)
对点练习:如图,在等边△ABC中,D、E、F分别是边BC、AC、AB的中点,则△AFE经过平移可以得到(%///%)
A.△DEF B.△FBD
C.△EDC D.△FBD和△EDC
D
对点练习:如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与点P′之间的距离为%///%,∠APB=%// //%.
6/
150°
对点练习:如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C.设点A的坐标为(a,b),则点A′的坐标为(%////%)
A.(-a,-b) B.(-a,-b-1)
C.(-a,-b+1) D.(-a,-b-2)
D
1.将长度为5 cm的线段向上平移10 cm后,所得线段的长度是(%////%)
A.10 cm B.5 cm
C.0 cm D.无法确定
B
2.以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是(%////%)
B
3.一个图形无论经过平移变换,还是经过旋转变换,下列说法正确的是(%////%)
①对应线段平行;②对应线段相等;③图形的形状和大小都没有发生变化;④对应角相等.
A.①②③ B.②③④
C.①②④ D.①③④
B
4.如图,△ABC和△BDE是等边三角形,点A、B、D在一条直线上,并且AB=BD .由一个三角形变换到另一个三角形(%///%)
A.仅能由平移得到
B.仅能由旋转得到
C.既能由平移得到,也能由旋转得到
D.既不能由平移得到,也不能由旋转得到
C/
5.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是(%////%)
A.(-3,2) B.(-1,2)
C.(1,2) D.(1,-2)
C
6.如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于(%////%)
A.55° B.70°
C.125° D.145°
C
7.如图,若△DEF是由△ABC经过平移后得到的,则平移的距离是(%////%)
A.线段BC的长度
B.线段BE的长度
C.线段EC的长度
D.线段EF的长度
B
8.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=(%////%)
A.30° B.35°
C.40° D.50°
C
9.在平面直角坐标系中,线段OP的两个端点坐标分别是O(0,0),P(4,3),将线段OP绕点O逆时针旋转90°到OP′位置,则点P′的坐标为(%////%)
A.(3,4) B.(-4,3)
C.(-3,4) D.(4,-3)
C
10.如图,△ABO中,AB⊥OB,OB=,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为(%////%)
A.(-1,-)
B.(-1,-)或(-2,0)
C.(-,-1)或(0,-2)
D.(-,-1)
B
11.如图,在四边形ABCD中,AD∥BC,BC>AD,∠B与∠C互余,将AB,CD分别平移到EF和EG的位置,则△EFG为%/// /%三角形.
直角
12.如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=%////%度.
20
13 .如图,在平面直角坐标系中,将线段AB绕点A按逆时针方向旋转90°后,得到线段AB′,则点B′的坐标为//% .
/(4,2)
14.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=%// //%.
20°
15.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C都是格点.
(1)将△ABC向左平移6个单位长度得到得到△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2,请画出△A2B2C2.
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求.
16.如图①,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:如图②,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是%// //%;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是%////%.
DE∥AC
解:(1)由旋转可知:CA=CD,
∵∠ACB=90°,∠B=30°,∴∠CAD=60°,
∴△ADC是等边三角形,∴∠DCA=60°,
∵∠ECD=90°,∠DEC=30°,∴∠CDE=60°,
∴∠EDC=∠DCA,∴DE∥AC,
②∵AB=2AC,AD=AC,∴AD=BD,∴S△BDC=S△ADC,
∵DE∥AC,∴S△ADC=S△ACE,∴S1=S2.
故答案为:DE∥AC,S1=S2.
(2)猜想论证:当△DEC绕点C旋转到如图③所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(2)∵△DEC是由△ABC旋转得到,∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=90°,
∴∠ACN=∠DCM,
在△ACN和△DCM中,,
∴△ACN≌△DCM(AAS),
∴AN=DM,∴S△BDC=S△AEC.
(3)拓展探究:已知∠ABC=60°,点D是角平分线上一点,BD=CD=6,DE∥AB交BC于点E(如图④).若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.
(3)如图中,作DF∥BC交AB于F.延长CD交AB于H.
∵DF∥BE,DE∥BF,∴四边形DEBF是平行四边形,
∴S△BDF=S△BDE,S△BDF=S△DFC,∴S△DFC=S△BDE,
∵∠ABC=60°,BD平分∠ABC,∴∠ABD=∠DBE=30°,
∵DF∥BE,∴∠FBD=∠FDB=30°,∴FB=FD,
∵BD=CD=6,∴∠DBC=∠DCB=30°,
∵∠DEC=∠ABC=60°,∴∠CDE=90°,
∴由勾股定理得DE=2,∴BF=DE=2,
∵DE∥AB,∴∠BHC=∠EDC=90°,
∴CH⊥AB,作点F关于CH的对称点F′,连接DF′,易知S△DFC=S△DF′C,
在Rt△DFH中,HD=BD=3,∴FH=HF′=,∴BF′=4,
综上所述,满足条件的BF的值为2或4.//
17.如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一种实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0).得到正方形A′B′C′D′及其内部的点,其中点A、B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
解:由点A到点A′,可得方程组;
由点B到点B′,可得方程组,
解得,
设F点的坐标为(x,y),点F′与点F重合得到方程组
解得,即F(1,4).
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
