【五环分层导学-课件】4.1分解因式-北师大版数学八(下)
文档属性
| 名称 | 【五环分层导学-课件】4.1分解因式-北师大版数学八(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 11:48:33 | ||
图片预览






文档简介
(共14张PPT)
第四章 因式分解
第1课 分解因式
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
(1)12能被%// //% 整除;
(2)想一想:993-99能被100整除吗?
%//
1,2,3,4,6,12
解:993-99=99×992-99×1
=99×(992-1)
=99×9800
=98×99×100,
所以993-99能被100整除.
【问题1】分析小明的做法是否合理
(1)993-99还能被哪些正整数整除?%// //%.
(2)解决问题(1)的关键是 .
98、99、11、9等
把一个数式分解成几个数的积的形式
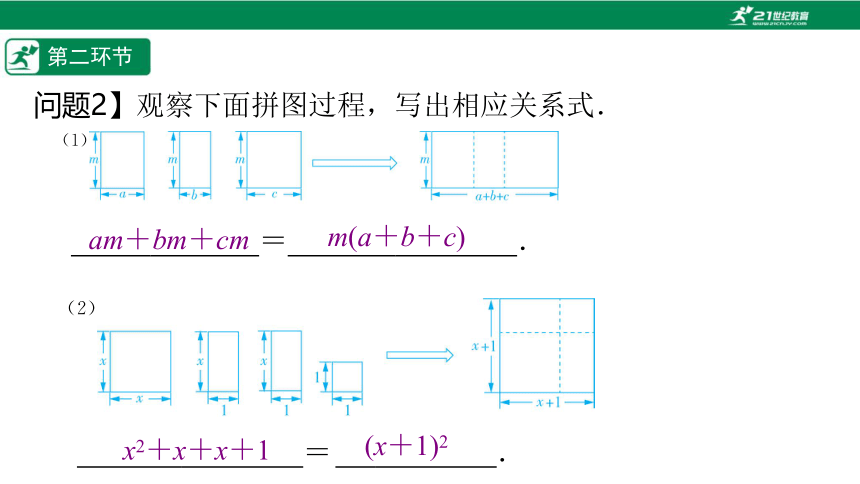
问题2】观察下面拼图过程,写出相应关系式.
%////% =%// //% .
%// //% = //% .
am+bm+cm
m(a+b+c)
x2+x+x+1
(x+1)2
【问题3】请你把a3-a化成几个整式的乘积的形式:a3-a= .
定义:把一个%// //%化成几个整式的%// //%的形式,这种变形叫做把这个多项式因式分解.也可以称分解因式.因式分解与整式的乘法正好互为逆运算.
对点练习:下列由左到右的变形中,是因式分解的打√.
①a(x+y)=ax+ay ( ) ②ax2-9a=a(x-3)(x+3) (%////%)
③10x2-5x=5x(2x-1) (%////%) ④y2-4y+4=(y-2)2 (%////%)
⑤t2-16+3t=(t+4)(t-4)+3t ( ) ⑥5x2y=5xxy ( )
a(a+1)(a-1)//
多项式
积
√
√
√
【例题1】计算下列式子(整式乘法):根据左边的算式进行因式分解:
(1)3x(x-1)= //; (5)3x2-3x= //;
(2)m(a+b-1)= ; (6)ma+mb-m= /;
(3)(m+4)(m-4)=// //; (7)m2-16= /;
(4)(y-3)2=%/ //; (8)y2-6y+9= /.
【例题2】分解因式:
(1)ax+ay=// ; (2)x2-9= ;
(3)y2-4y+4=// .
3x2-3x
3x(x-1)
am+bm-1
m(a+b-1)
m2-16
%(m+4)(m-4)
y2-6y+9
/(y-3)2
a(x+y)
/(x+3)(x-3)//
//(y-2)2
【例题3】20192+2019能被2020整除吗?
解:20192+2019=2019(2019+1)=2019×2020,
所以20192+2019能被2020整除.
1.下列由左边到右边的变形中,属于因式分解的是(%////%)
A.x2+3x+4=(x+2)(x+1)+2 B.6x2y3=3xy·2xy2
C.(3x-2)(2x+1)=6x2-x-2 D.4ab+2ac=2a(2b+c)
D
2.(3a-y)(3a+y)是下列哪一个多项式因式分解的结果(%////%)
A.9a2+y2 B.-9a2+y2
C.9a2-y2 D.-9a2-y2
C
3.分解因式:
(1)xy-y2=%// //%;
(2)9-25x2= /% ;
(3)x2-y2= % .
y(x-y)
/(3+5x)(3-5x)/
(x+y)(x-y)//
4.16.9×+15.1×能被4整除吗?
解:16.9×+15.1×(16.9+15.1)=×32=4,
所以16.9×+15.1×能被4整除.
5.若因式分解x2+mx-15=(x+3)(x+n),求m、n的值.
解:∵(x+3)(x+n)=x2+nx+3x+3n=x2+(n+3)x+3n=x2+mx-15,
∴3n=-15,n+3=m,
∴n=-5,m=-2.
第四章 因式分解
第1课 分解因式
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
(1)12能被%// //% 整除;
(2)想一想:993-99能被100整除吗?
%//
1,2,3,4,6,12
解:993-99=99×992-99×1
=99×(992-1)
=99×9800
=98×99×100,
所以993-99能被100整除.
【问题1】分析小明的做法是否合理
(1)993-99还能被哪些正整数整除?%// //%.
(2)解决问题(1)的关键是 .
98、99、11、9等
把一个数式分解成几个数的积的形式
问题2】观察下面拼图过程,写出相应关系式.
%////% =%// //% .
%// //% = //% .
am+bm+cm
m(a+b+c)
x2+x+x+1
(x+1)2
【问题3】请你把a3-a化成几个整式的乘积的形式:a3-a= .
定义:把一个%// //%化成几个整式的%// //%的形式,这种变形叫做把这个多项式因式分解.也可以称分解因式.因式分解与整式的乘法正好互为逆运算.
对点练习:下列由左到右的变形中,是因式分解的打√.
①a(x+y)=ax+ay ( ) ②ax2-9a=a(x-3)(x+3) (%////%)
③10x2-5x=5x(2x-1) (%////%) ④y2-4y+4=(y-2)2 (%////%)
⑤t2-16+3t=(t+4)(t-4)+3t ( ) ⑥5x2y=5xxy ( )
a(a+1)(a-1)//
多项式
积
√
√
√
【例题1】计算下列式子(整式乘法):根据左边的算式进行因式分解:
(1)3x(x-1)= //; (5)3x2-3x= //;
(2)m(a+b-1)= ; (6)ma+mb-m= /;
(3)(m+4)(m-4)=// //; (7)m2-16= /;
(4)(y-3)2=%/ //; (8)y2-6y+9= /.
【例题2】分解因式:
(1)ax+ay=// ; (2)x2-9= ;
(3)y2-4y+4=// .
3x2-3x
3x(x-1)
am+bm-1
m(a+b-1)
m2-16
%(m+4)(m-4)
y2-6y+9
/(y-3)2
a(x+y)
/(x+3)(x-3)//
//(y-2)2
【例题3】20192+2019能被2020整除吗?
解:20192+2019=2019(2019+1)=2019×2020,
所以20192+2019能被2020整除.
1.下列由左边到右边的变形中,属于因式分解的是(%////%)
A.x2+3x+4=(x+2)(x+1)+2 B.6x2y3=3xy·2xy2
C.(3x-2)(2x+1)=6x2-x-2 D.4ab+2ac=2a(2b+c)
D
2.(3a-y)(3a+y)是下列哪一个多项式因式分解的结果(%////%)
A.9a2+y2 B.-9a2+y2
C.9a2-y2 D.-9a2-y2
C
3.分解因式:
(1)xy-y2=%// //%;
(2)9-25x2= /% ;
(3)x2-y2= % .
y(x-y)
/(3+5x)(3-5x)/
(x+y)(x-y)//
4.16.9×+15.1×能被4整除吗?
解:16.9×+15.1×(16.9+15.1)=×32=4,
所以16.9×+15.1×能被4整除.
5.若因式分解x2+mx-15=(x+3)(x+n),求m、n的值.
解:∵(x+3)(x+n)=x2+nx+3x+3n=x2+(n+3)x+3n=x2+mx-15,
∴3n=-15,n+3=m,
∴n=-5,m=-2.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
