【五环分层导学-课件】6-7 多边形的内角和(1)-北师大版数学八(下)
文档属性
| 名称 | 【五环分层导学-课件】6-7 多边形的内角和(1)-北师大版数学八(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 11:48:33 | ||
图片预览




文档简介
(共13张PPT)
第六章 平行四边形
第7课 多边形的内角和(1)
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
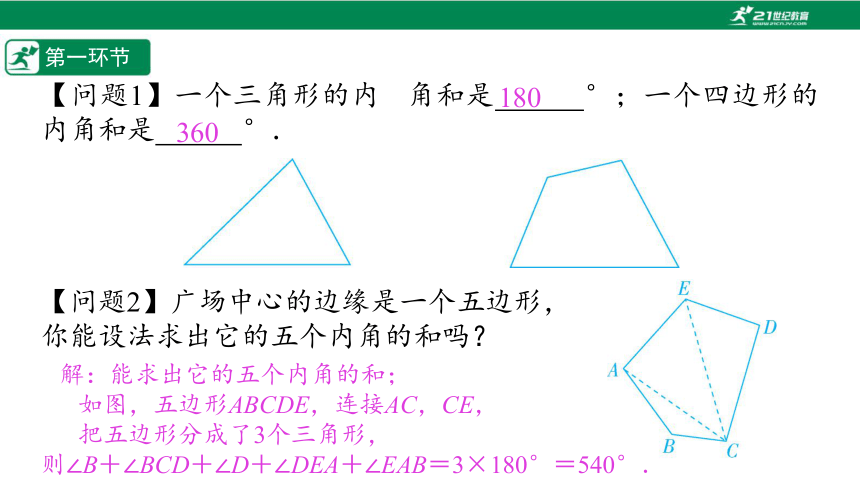
【问题1】一个三角形的内 角和是%// //%°;一个四边形的内角和是%// //%°.
【问题2】广场中心的边缘是一个五边形,
你能设法求出它的五个内角的和吗?
解:能求出它的五个内角的和;
如图,五边形ABCDE,连接AC,CE,
把五边形分成了3个三角形,
则∠B+∠BCD+∠D+∠DEA+∠EAB=3×180°=540°.
180
360
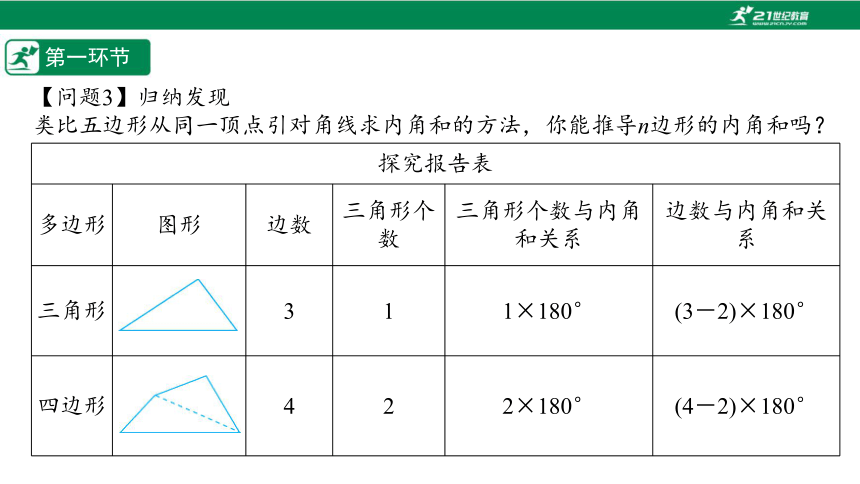
【问题3】归纳发现
类比五边形从同一顶点引对角线求内角和的方法,你能推导n边形的内角和吗?
探究报告表 多边形 图形 边数 三角形个数 三角形个数与内角和关系 边数与内角和关系
三角形 3 1 1×180° (3-2)×180°
四边形 4 2 2×180° (4-2)×180°
五边形 5
六边形 6
七边形 7
… … …
n边形 n
n边形内角和公式:%// %
(n-2)×180°//
%//3//% 3×180° (5-2)×180°
%//4//% 4×180° (6-2)×180°
%//5//% 5×180° (7-2)×180°
… … …
n-2 (n-2)×180° (n-2)×180°
【问题4】按照如图的方法,五边形能分成多少个三角形?n边形呢?你能确定n边形的内角和吗?你还有其他方法吗?
解:由如图的方法,可以把五边形分成5个三角形,五边形的内角和=5×180°-360°=(5-2)×180°;
由如图的方法,可以把n边形分成n个三角形,n边形的内角和=n×180°-360°=(n-2)×180°.
【例题1】剪掉一张长方形纸片的一个角,纸片还剩下几个角?得到的新多边形的内角和是多少度?
解:因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,当截线为经过长方形对角2个顶点的直线时,剩余图形为三角形,内角和为180°;
当截线为经过长方形一组对边的直线时,剩余图形是四边形,内角和360°;
当截线为只经过长方形一组邻边的一条直线时,剩余图形是五边形,内角和为540°./
【例题2】学校要建一个花坛,向全校师生征求创新设计方案.小红想要设计一个内角和是2010°的多边形花坛,请问:小红的这个想法能实现吗?为什么?
解:不能实现.理由如下:
设边数为n,根据题意,
得(n-2) 180°=2010°,
解得n=13.
∵边数n为正整数,
∴她的愿望不能实现.
1.(1)六边形的内角和等于%// //%°.一个多边形的内角和等于900°,则它是%// //%边形.
(2)正五边形的每一个内角都等于%// //%°;一个多边形的每一个内角都是120°,那么它是%// //%.
720
七
108
正六边形
2.如图,四边形ABCD中,∠A+∠C=180°,∠B与∠D有怎样的关系?
解:∵四边形的内角和是360°,
又∵∠A+∠C=180°,
∴∠B+∠D=180°,即∠B与∠D互补.
3.(★)想一想:观察图中的多边形,它们的边、角有什么特点?
像这样所有的边长%// //%,所有的%// //%相等的多边形叫做“正多边形”.
(1)正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度?
都相等
内角都
解:正三角形的内角都是60°,正方形的内角都是90°,正五边形的内角都是108°,正六边形的内角都是120°,正八边形的内角都是135°;
(2)正n边形的内角是多少度?
(3)一个正多边形的每个内角都是150°,求它的边数?
解:正n边形的内角是;
解:一个正多边形的每个内角都是150°,
即=150°,解得n=12,
故它的边数是12.
第六章 平行四边形
第7课 多边形的内角和(1)
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
【问题1】一个三角形的内 角和是%// //%°;一个四边形的内角和是%// //%°.
【问题2】广场中心的边缘是一个五边形,
你能设法求出它的五个内角的和吗?
解:能求出它的五个内角的和;
如图,五边形ABCDE,连接AC,CE,
把五边形分成了3个三角形,
则∠B+∠BCD+∠D+∠DEA+∠EAB=3×180°=540°.
180
360
【问题3】归纳发现
类比五边形从同一顶点引对角线求内角和的方法,你能推导n边形的内角和吗?
探究报告表 多边形 图形 边数 三角形个数 三角形个数与内角和关系 边数与内角和关系
三角形 3 1 1×180° (3-2)×180°
四边形 4 2 2×180° (4-2)×180°
五边形 5
六边形 6
七边形 7
… … …
n边形 n
n边形内角和公式:%// %
(n-2)×180°//
%//3//% 3×180° (5-2)×180°
%//4//% 4×180° (6-2)×180°
%//5//% 5×180° (7-2)×180°
… … …
n-2 (n-2)×180° (n-2)×180°
【问题4】按照如图的方法,五边形能分成多少个三角形?n边形呢?你能确定n边形的内角和吗?你还有其他方法吗?
解:由如图的方法,可以把五边形分成5个三角形,五边形的内角和=5×180°-360°=(5-2)×180°;
由如图的方法,可以把n边形分成n个三角形,n边形的内角和=n×180°-360°=(n-2)×180°.
【例题1】剪掉一张长方形纸片的一个角,纸片还剩下几个角?得到的新多边形的内角和是多少度?
解:因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,当截线为经过长方形对角2个顶点的直线时,剩余图形为三角形,内角和为180°;
当截线为经过长方形一组对边的直线时,剩余图形是四边形,内角和360°;
当截线为只经过长方形一组邻边的一条直线时,剩余图形是五边形,内角和为540°./
【例题2】学校要建一个花坛,向全校师生征求创新设计方案.小红想要设计一个内角和是2010°的多边形花坛,请问:小红的这个想法能实现吗?为什么?
解:不能实现.理由如下:
设边数为n,根据题意,
得(n-2) 180°=2010°,
解得n=13.
∵边数n为正整数,
∴她的愿望不能实现.
1.(1)六边形的内角和等于%// //%°.一个多边形的内角和等于900°,则它是%// //%边形.
(2)正五边形的每一个内角都等于%// //%°;一个多边形的每一个内角都是120°,那么它是%// //%.
720
七
108
正六边形
2.如图,四边形ABCD中,∠A+∠C=180°,∠B与∠D有怎样的关系?
解:∵四边形的内角和是360°,
又∵∠A+∠C=180°,
∴∠B+∠D=180°,即∠B与∠D互补.
3.(★)想一想:观察图中的多边形,它们的边、角有什么特点?
像这样所有的边长%// //%,所有的%// //%相等的多边形叫做“正多边形”.
(1)正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度?
都相等
内角都
解:正三角形的内角都是60°,正方形的内角都是90°,正五边形的内角都是108°,正六边形的内角都是120°,正八边形的内角都是135°;
(2)正n边形的内角是多少度?
(3)一个正多边形的每个内角都是150°,求它的边数?
解:正n边形的内角是;
解:一个正多边形的每个内角都是150°,
即=150°,解得n=12,
故它的边数是12.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
