【五环分层导学-课件】6-9 单元复习 平行四边形-北师大版数学八(下)
文档属性
| 名称 | 【五环分层导学-课件】6-9 单元复习 平行四边形-北师大版数学八(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 21.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 11:48:33 | ||
图片预览











文档简介
(共35张PPT)
第六章 平行四边形
第1课 单元复习
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】什么叫做平行四边形?生活中哪些东西可以看做平行四边形?
【问题2】平行四边形有什么性质?
【问题3】如何判定一个四边形是平行四边形?
【问题4】任意画一个四边形,依次连接它的各边中点,你能得到一个怎样的四边形?
【问题5】多边形的内角和、外角和有什么规律?
【问题6】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点等)呈现全章的知识结构.
【例题1】如图,将□ABCD的一边BC延长至点E,若∠A=110°,则∠1=(%////%)
A.110° B.35°
C.70° D.55°
C
【例题2】平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为(%////%)
A.4,4,8,8 B.5,5,7,7
C.5.5,5.5,6.5,6.5 D.3,3,9,9
【例题3】如图,在□ABCD中,∠A=60°,BE⊥AD,BF⊥CD,AE=2,BF=3.则□ABCD的面积为%// //%.
B
12
【例题4】如图,已知点A(3,0)、B(-1,0)、C(0,2),以A、B、C为顶点画平行四边形,你能求出第四个顶点D吗?
解:①如图①,以AB为边时,
A(3,0)、B(-1,0)两点之间的距离为:3-(-1)=4,
∴第四个顶点的纵坐标为2,横坐标为0+4=4,或0-4=-4,
即D(4,2)或D′(-4,2);
②如图②,以AB为对角线时,
∵从C(0,2)到B(-1,0),是横坐标减1,纵坐标减2,
∴第四个顶点D的横坐标为:
3-1=2,纵坐标为0-2=-2,
即D(2,-2),
综上所述,第四个顶点D的坐标为(4,2)或(-4,2)或(2,-2).
【例题1】下列各组条件中,不能判定四边形ABCD是平行四边形的是(%////%)
A.AB=CD,AD=BC B.AB//CD,AB=CD
C.AD//BC,AB=CD D.AB//CD,AD//BC
【例题2】四边形ABCD的四个角∠A∶∠B∶∠C∶∠D满足下列哪一条件时,四边形ABCD是平行四边形(%////%)
A.1∶2∶2∶1 B.2∶1∶1∶1 C.1∶2∶3∶4 D.2∶1∶2∶1
C
D
【例题3】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB,AC于点F,G,连接BE.
(1)如图①所示,当点D在线段BC上时,
①求证:△AEB≌△ADC;②探究四边形BCGE是怎样特殊四边形?并说明理由.
(2)如图②所示,当点D在BC的延长线上时,直接写出(1)中的两个结论是否成立?
(1)证明:①∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°.
又∵∠EAB=∠EAD-∠BAD,
∠DAC=∠BAC-∠BAD,
∴∠EAB=∠DAC,
∴△AEB≌△ADC(SAS).
②由①得△AEB≌△ADC,∴∠ABE=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABE=∠BAC,∴EB//GC .
又∵EG//BC,∴四边形BCGE是平行四边形.
(2)解:①②都成立.
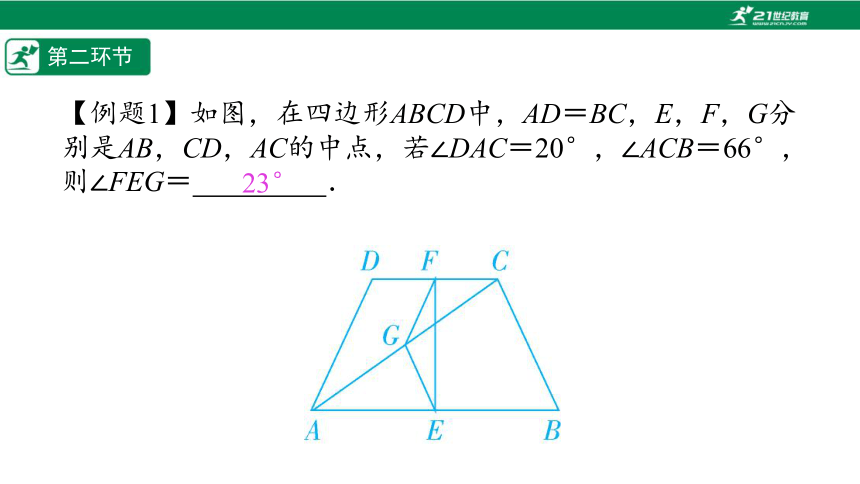
【例题1】如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,若∠DAC=20°,∠ACB=66°,则∠FEG=%// //%.
23°
【例题2】如图,D、E是△ABC的边AB和AC中点,延长DE到F,使EF=DE,连接CF.求证:四边形BCFD是平行四边形.
解:四边形BCFD是平行四边形;理由如下:
∵D、E是△ABC的边AB和AC中点,
∴DE是△ABC的中位线,
∴DE//BC,DE=BC,
∵EF=DE,∴DF=BC,
∴四边形BCFD是平行四边形.
【例题1】过多边形的某个顶点的所有对角线,将这个多边形分成7个三角形,则这个是%////%边形,它的内角和是%// //%,外角和是%// //%.
【例题2】如图,直线GH与正六边形ABCDEF的边AB、EF分别交于点G、H,∠AGH=48°,则∠GHF的度数为%// //%.
九
1260°
360°
72°
【例题3】如图,用一条宽相等的足够长的纸条,打一个结,如图①所示,然后轻轻拉紧、压平就可以得到如图②所示的正五边形ABCDE,其中∠BAC=(%////%)
A.30° B.36°
C.40° D.72°
B
对点练习:如图,某广场有一个形状是平行四边形的花坛,分别种有红黄蓝绿橙紫6种色的花,如果有AB//EF//DC,BC//GH//AD,那么下列说法错误的是(%////%)
A.红花,绿花种植面积一定相等
B.紫花,橙花种植面积一定相等
C.红花,蓝花种植面积一定相等
D.蓝花,黄花种植面积一定相等
C
对点练习:线段BD是平行四边形ABCD的对角线,E、F分别为BC、AD上任意一点,连接EF交BD于点P,判断PE和PF的大小关系(%////%)
A.PE=PF B.PE>PF
C.PE<PF D.以上都有可能
D
对点练习:□ABCD一内角的平分线与边相交并把这条边分成5 cm,7 cm的两条线段,则□ABCD的周长是%// //% cm.
34或38
1.一个正多边形的每个外角都是36°,这个正多边形的边数是(%////%)
A.9 B.10 C.11 D.12
B
2.平行四边形的两条对角线分别为6和10,则其中一条边x的取值范围为(%////%)
A.4<x<6 B.2<x<8 C.0<x<10 D.0<x<6
B
3.如图,四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是(%////%)
A.AB//DC,AD//BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB//DC,AD=BC
D
4.如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是(%////%)
A.S□ABCD=4S△AOB
B.AC=BD
C.AC⊥BD
D.□ABCD是轴对称图形
A
5.如图,点E是□ABCD的边CD的中点,AD,BE的延长线相交于点F,DF=3,DE=2,则□ABCD的周长为(%////%)
A.5 B.7
C.10 D.14
D
6.如图所示,线段a、b、c的端点分别在直线l1、l2上,则下列说法中正确的是(%////%)
A.若l1//l2,则a=b
B.若l1//l2,则a=c
C.若a//b,则a=b
D.若l1//l2,且a//b,则a=b
D
7.如图,在□ABCD中,AM⊥BD于点M,且BM∶DM=1∶2,BD=12,AD=10,则□ABCD的面积是(%////%)
A.30 B.36
C.54 D.72
D
8.如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有□ADCE中,DE最小的值是(%////%)
A.2 B.3
C.4 D.5
B
9.如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是(%////%)
A.①②③ B.①②④
C.①②⑤ D.①③④
C
10.在四边形ABCD中,AB//CD,AD//BC,如果∠B=50°,则∠D=%// //%.
50°
11.如图所示,在平行四边形ABCD中,E、F分别为AD、BC边上的一点,若添加一个条件%// //%,则四边形EBFD为平行四边形(只填一个条件即可).
AE=CF
12.如图,在□ABCD中,点O是对角线AC、BD的交点,点E是边CD的中点,且AB=6,BC=10,则OE=%////%.
5
13.已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示.若点C、D也在小方格的顶点上,这四点正好是一个平行四边形的四个顶点,且这个平行四边形的面积恰好为2,则这样的平行四边形有%////%个.
6
14.如图所示,已知在平行四边形ABCD中,BE=DF,求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴DC=BA,DC//BA,∴∠CDF=∠ABE,
在△DCF和△BAE中,,
∴△DCF≌△BAE(SAS),∴AE=CF.
15.如图,已知BE//DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.
证明:∵BE//DF,∴∠BEC=∠DFA,
在△ADF和△CBE中,
∴△ADF≌△CBE(AAS),∴BE=DF,
又∵BE//DF,∴四边形DEBF是平行四边形.
16.如图,在六边形ABCDEF中,AB⊥AF,BC⊥DC,∠E+∠F=260°,求两外角和∠α+∠β的度数.
解:∵AB⊥AF,BC⊥DC,
∴∠A+∠C=180°,
∵∠E+∠F=260°,
∴∠EDC+∠ABC=(6-2)×180°-180°-260°=280°,
∴∠α+∠β=360°-(∠EDC+∠ABC)=80°.
故两外角和∠α+∠β的度数为80°.
17.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF//AC交直线AB于点F,DE//AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,
则DF=%// //%.
(1)证明:∵DF//AC,DE//AB,
∴四边形AFDE是平行四边形.
∴AF=DE,∵DF//AC,
∴∠FDB=∠C,又∵AB=AC,
∴∠B=∠C,∴∠FDB=∠B,
∴DF=BF,
∴DE+DF=AB=AC;
(2)解:图②中:AC+DE=DF.图③中:AC+DF=DE.
(3)解:当如图①的情况,DF=AC-DE=6-4=2;
当如图②的情况,DF=AC+DE=6+4=10.
故答案是:2或10.
第六章 平行四边形
第1课 单元复习
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】什么叫做平行四边形?生活中哪些东西可以看做平行四边形?
【问题2】平行四边形有什么性质?
【问题3】如何判定一个四边形是平行四边形?
【问题4】任意画一个四边形,依次连接它的各边中点,你能得到一个怎样的四边形?
【问题5】多边形的内角和、外角和有什么规律?
【问题6】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点等)呈现全章的知识结构.
【例题1】如图,将□ABCD的一边BC延长至点E,若∠A=110°,则∠1=(%////%)
A.110° B.35°
C.70° D.55°
C
【例题2】平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为(%////%)
A.4,4,8,8 B.5,5,7,7
C.5.5,5.5,6.5,6.5 D.3,3,9,9
【例题3】如图,在□ABCD中,∠A=60°,BE⊥AD,BF⊥CD,AE=2,BF=3.则□ABCD的面积为%// //%.
B
12
【例题4】如图,已知点A(3,0)、B(-1,0)、C(0,2),以A、B、C为顶点画平行四边形,你能求出第四个顶点D吗?
解:①如图①,以AB为边时,
A(3,0)、B(-1,0)两点之间的距离为:3-(-1)=4,
∴第四个顶点的纵坐标为2,横坐标为0+4=4,或0-4=-4,
即D(4,2)或D′(-4,2);
②如图②,以AB为对角线时,
∵从C(0,2)到B(-1,0),是横坐标减1,纵坐标减2,
∴第四个顶点D的横坐标为:
3-1=2,纵坐标为0-2=-2,
即D(2,-2),
综上所述,第四个顶点D的坐标为(4,2)或(-4,2)或(2,-2).
【例题1】下列各组条件中,不能判定四边形ABCD是平行四边形的是(%////%)
A.AB=CD,AD=BC B.AB//CD,AB=CD
C.AD//BC,AB=CD D.AB//CD,AD//BC
【例题2】四边形ABCD的四个角∠A∶∠B∶∠C∶∠D满足下列哪一条件时,四边形ABCD是平行四边形(%////%)
A.1∶2∶2∶1 B.2∶1∶1∶1 C.1∶2∶3∶4 D.2∶1∶2∶1
C
D
【例题3】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB,AC于点F,G,连接BE.
(1)如图①所示,当点D在线段BC上时,
①求证:△AEB≌△ADC;②探究四边形BCGE是怎样特殊四边形?并说明理由.
(2)如图②所示,当点D在BC的延长线上时,直接写出(1)中的两个结论是否成立?
(1)证明:①∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°.
又∵∠EAB=∠EAD-∠BAD,
∠DAC=∠BAC-∠BAD,
∴∠EAB=∠DAC,
∴△AEB≌△ADC(SAS).
②由①得△AEB≌△ADC,∴∠ABE=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABE=∠BAC,∴EB//GC .
又∵EG//BC,∴四边形BCGE是平行四边形.
(2)解:①②都成立.
【例题1】如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,若∠DAC=20°,∠ACB=66°,则∠FEG=%// //%.
23°
【例题2】如图,D、E是△ABC的边AB和AC中点,延长DE到F,使EF=DE,连接CF.求证:四边形BCFD是平行四边形.
解:四边形BCFD是平行四边形;理由如下:
∵D、E是△ABC的边AB和AC中点,
∴DE是△ABC的中位线,
∴DE//BC,DE=BC,
∵EF=DE,∴DF=BC,
∴四边形BCFD是平行四边形.
【例题1】过多边形的某个顶点的所有对角线,将这个多边形分成7个三角形,则这个是%////%边形,它的内角和是%// //%,外角和是%// //%.
【例题2】如图,直线GH与正六边形ABCDEF的边AB、EF分别交于点G、H,∠AGH=48°,则∠GHF的度数为%// //%.
九
1260°
360°
72°
【例题3】如图,用一条宽相等的足够长的纸条,打一个结,如图①所示,然后轻轻拉紧、压平就可以得到如图②所示的正五边形ABCDE,其中∠BAC=(%////%)
A.30° B.36°
C.40° D.72°
B
对点练习:如图,某广场有一个形状是平行四边形的花坛,分别种有红黄蓝绿橙紫6种色的花,如果有AB//EF//DC,BC//GH//AD,那么下列说法错误的是(%////%)
A.红花,绿花种植面积一定相等
B.紫花,橙花种植面积一定相等
C.红花,蓝花种植面积一定相等
D.蓝花,黄花种植面积一定相等
C
对点练习:线段BD是平行四边形ABCD的对角线,E、F分别为BC、AD上任意一点,连接EF交BD于点P,判断PE和PF的大小关系(%////%)
A.PE=PF B.PE>PF
C.PE<PF D.以上都有可能
D
对点练习:□ABCD一内角的平分线与边相交并把这条边分成5 cm,7 cm的两条线段,则□ABCD的周长是%// //% cm.
34或38
1.一个正多边形的每个外角都是36°,这个正多边形的边数是(%////%)
A.9 B.10 C.11 D.12
B
2.平行四边形的两条对角线分别为6和10,则其中一条边x的取值范围为(%////%)
A.4<x<6 B.2<x<8 C.0<x<10 D.0<x<6
B
3.如图,四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是(%////%)
A.AB//DC,AD//BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB//DC,AD=BC
D
4.如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是(%////%)
A.S□ABCD=4S△AOB
B.AC=BD
C.AC⊥BD
D.□ABCD是轴对称图形
A
5.如图,点E是□ABCD的边CD的中点,AD,BE的延长线相交于点F,DF=3,DE=2,则□ABCD的周长为(%////%)
A.5 B.7
C.10 D.14
D
6.如图所示,线段a、b、c的端点分别在直线l1、l2上,则下列说法中正确的是(%////%)
A.若l1//l2,则a=b
B.若l1//l2,则a=c
C.若a//b,则a=b
D.若l1//l2,且a//b,则a=b
D
7.如图,在□ABCD中,AM⊥BD于点M,且BM∶DM=1∶2,BD=12,AD=10,则□ABCD的面积是(%////%)
A.30 B.36
C.54 D.72
D
8.如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有□ADCE中,DE最小的值是(%////%)
A.2 B.3
C.4 D.5
B
9.如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是(%////%)
A.①②③ B.①②④
C.①②⑤ D.①③④
C
10.在四边形ABCD中,AB//CD,AD//BC,如果∠B=50°,则∠D=%// //%.
50°
11.如图所示,在平行四边形ABCD中,E、F分别为AD、BC边上的一点,若添加一个条件%// //%,则四边形EBFD为平行四边形(只填一个条件即可).
AE=CF
12.如图,在□ABCD中,点O是对角线AC、BD的交点,点E是边CD的中点,且AB=6,BC=10,则OE=%////%.
5
13.已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示.若点C、D也在小方格的顶点上,这四点正好是一个平行四边形的四个顶点,且这个平行四边形的面积恰好为2,则这样的平行四边形有%////%个.
6
14.如图所示,已知在平行四边形ABCD中,BE=DF,求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴DC=BA,DC//BA,∴∠CDF=∠ABE,
在△DCF和△BAE中,,
∴△DCF≌△BAE(SAS),∴AE=CF.
15.如图,已知BE//DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.
证明:∵BE//DF,∴∠BEC=∠DFA,
在△ADF和△CBE中,
∴△ADF≌△CBE(AAS),∴BE=DF,
又∵BE//DF,∴四边形DEBF是平行四边形.
16.如图,在六边形ABCDEF中,AB⊥AF,BC⊥DC,∠E+∠F=260°,求两外角和∠α+∠β的度数.
解:∵AB⊥AF,BC⊥DC,
∴∠A+∠C=180°,
∵∠E+∠F=260°,
∴∠EDC+∠ABC=(6-2)×180°-180°-260°=280°,
∴∠α+∠β=360°-(∠EDC+∠ABC)=80°.
故两外角和∠α+∠β的度数为80°.
17.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF//AC交直线AB于点F,DE//AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,
则DF=%// //%.
(1)证明:∵DF//AC,DE//AB,
∴四边形AFDE是平行四边形.
∴AF=DE,∵DF//AC,
∴∠FDB=∠C,又∵AB=AC,
∴∠B=∠C,∴∠FDB=∠B,
∴DF=BF,
∴DE+DF=AB=AC;
(2)解:图②中:AC+DE=DF.图③中:AC+DF=DE.
(3)解:当如图①的情况,DF=AC-DE=6-4=2;
当如图②的情况,DF=AC+DE=6+4=10.
故答案是:2或10.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
