【五环分层导学-课件】1-6 直角三角形(2)-北师大版数学八(下)
文档属性
| 名称 | 【五环分层导学-课件】1-6 直角三角形(2)-北师大版数学八(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 11:48:33 | ||
图片预览






文档简介
(共15张PPT)
第一章 三角形的证明
第6课 直角三角形(2)
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
图形 直角三角形性质 直角三角形判定
(1)直角三角形的两锐角互余. (2)勾股定理:直角三角形的两直角的平方和等于斜边的平方. (3)如果直角三角形中有一个角等于30°,那么它所对的直角边等于斜边的一半 (1)有两个角互余的三角形是直角三角形.
(2)勾股定理逆定理:如果三角形的两边平方和等于第三边的平方,那 么这个三角形是直角三角形.
【问题1】忆一忆:判断两个三角形全等的方法有哪几种?
【问题2】画一画:已知一条直角边和斜边,求作一个直角三角形
已知:如图,线段a、c(a<c)和直角α.
求作:Rt△ABC,使∠C=α,直角边AC=a,斜边AB=c.
解:如图,作∠C=90°,在一边上截取CA=a,以A为顶点c为半径作弧,交另一直角边于点B.Rt△ABC就是所求的直角三角形.
【问题3】猜一猜:你作的三角形和同桌作的三角形全等吗?
由此我们可以猜想:%// //%.
解:全等
斜边和一条直角边分别相等的两个直角三角形全等
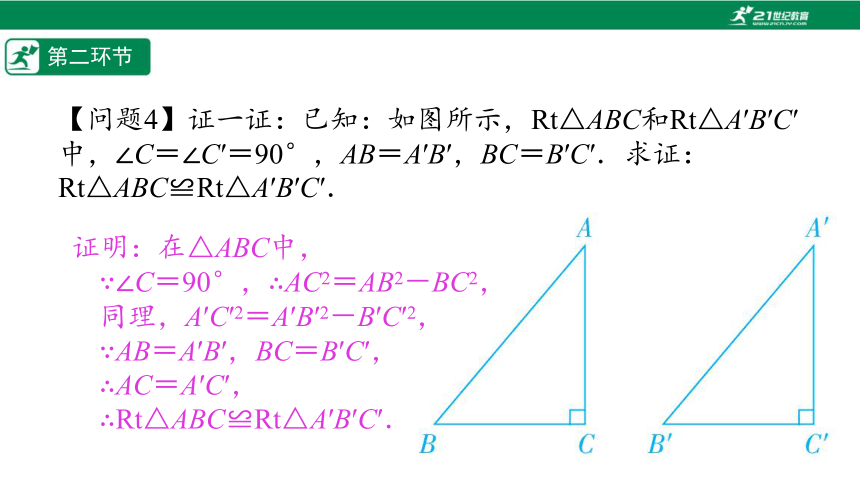
【问题4】证一证:已知:如图所示,Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,AB=A′B′,BC=B′C′.求证:Rt△ABC≌Rt△A′B′C′.
证明:在△ABC中,
∵∠C=90°,∴AC2=AB2-BC2,
同理,A′C′2=A′B′2-B′C′2,
∵AB=A′B′,BC=B′C′,
∴AC=A′C′,
∴Rt△ABC≌Rt△A′B′C′.
定理:%// //%和%// //%分别相等的两个直角三角形全等.(可简写成为“斜边、直角边”或“HL”)
几何语言:在Rt△ABC和Rt△A′B′C′中,
∵,∴△ABC≌△A′B′C′(%//HL//%).
∵,∴△ABC≌△A′B′C′(%//HL//%).
斜边
一条直角边
【例题1】如图,AE⊥BC,DF⊥BC,垂足分别为E,F,AE=DF,AB=DC,求证:△AEB≌Rt△DFC.
∵%//AE⊥BC,DF⊥BC//%,
%//AE=DF,AB=DC//%,
∴%//△AEB//%≌%//△DFC//%(%//HL//%).
∵%//AE⊥BC,DF⊥BC//%,
%//AE=DF,AB=DC//%,
∴%//△AEB//%≌%//△DFC//%(%//HL//%).
【例题2】如图所示,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解:∠B+∠F=90°;理由如下:
∵∠CAB=∠EDF=90°,
BC=EF,AC=DF,
∴△ACB≌△DFE,
∴∠B=∠DEF,
∵∠DEF+∠F=90°,
∴∠B+∠F=90°.
【例题3】已知:如图,D是△ABC的BC边的中点,DE⊥AC,DF⊥AB,垂足分别为E,F.且DE=DF.
求证:△ABC是等腰三角形.
证明:∵D是△ABC的BC边的中点,
∴BD=CD,
又∵DE⊥AC,DF⊥AB,DE=DF,
∴△DFB≌△DEC,
∴∠B=∠C,∴AB=AC,
∴△ABC是等腰三角形.
1.如图,O是∠BAC内一点,且点O到AB,AC的距离OE=OF,则△AEO≌△AFO的依据是(%////%)
A.HL
B.AAS
C.SSS
D.ASA
A
2.判断下列命题的真假,并说明理由:
(1)两个锐角分别相等的两个直角三角形全等. (%////%)
(2)斜边及一锐角分别相等的两个直角三角形全等. (%////%)
(3)两条直角边分别相等的两个直角三角形全等. (%////%)
(4)一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等. (%////%)
假
真
真
真
3.如图,CD⊥AD,CB⊥AB,AB=AD .求证:CD=CB .
证明:连接AC,
∵CD⊥AD,CB⊥AB,AB=AD,
∴△ABC≌△ADC,
∴CB=CD .
4.已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,且DE=BF.
求证:(1)AE=CF; (2)AB//CD .
证明:(1)∵AB=CD,DE⊥AC,BF⊥AC,DE=BF,
∴△ABF≌△CDE,
∴AF=CE,
∴AF-EF=CE-EF,即AE=CF;
(2)由(1)得△ABF≌△CDE,
∴∠A=∠C,∴AB//CD .
第一章 三角形的证明
第6课 直角三角形(2)
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
图形 直角三角形性质 直角三角形判定
(1)直角三角形的两锐角互余. (2)勾股定理:直角三角形的两直角的平方和等于斜边的平方. (3)如果直角三角形中有一个角等于30°,那么它所对的直角边等于斜边的一半 (1)有两个角互余的三角形是直角三角形.
(2)勾股定理逆定理:如果三角形的两边平方和等于第三边的平方,那 么这个三角形是直角三角形.
【问题1】忆一忆:判断两个三角形全等的方法有哪几种?
【问题2】画一画:已知一条直角边和斜边,求作一个直角三角形
已知:如图,线段a、c(a<c)和直角α.
求作:Rt△ABC,使∠C=α,直角边AC=a,斜边AB=c.
解:如图,作∠C=90°,在一边上截取CA=a,以A为顶点c为半径作弧,交另一直角边于点B.Rt△ABC就是所求的直角三角形.
【问题3】猜一猜:你作的三角形和同桌作的三角形全等吗?
由此我们可以猜想:%// //%.
解:全等
斜边和一条直角边分别相等的两个直角三角形全等
【问题4】证一证:已知:如图所示,Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,AB=A′B′,BC=B′C′.求证:Rt△ABC≌Rt△A′B′C′.
证明:在△ABC中,
∵∠C=90°,∴AC2=AB2-BC2,
同理,A′C′2=A′B′2-B′C′2,
∵AB=A′B′,BC=B′C′,
∴AC=A′C′,
∴Rt△ABC≌Rt△A′B′C′.
定理:%// //%和%// //%分别相等的两个直角三角形全等.(可简写成为“斜边、直角边”或“HL”)
几何语言:在Rt△ABC和Rt△A′B′C′中,
∵,∴△ABC≌△A′B′C′(%//HL//%).
∵,∴△ABC≌△A′B′C′(%//HL//%).
斜边
一条直角边
【例题1】如图,AE⊥BC,DF⊥BC,垂足分别为E,F,AE=DF,AB=DC,求证:△AEB≌Rt△DFC.
∵%//AE⊥BC,DF⊥BC//%,
%//AE=DF,AB=DC//%,
∴%//△AEB//%≌%//△DFC//%(%//HL//%).
∵%//AE⊥BC,DF⊥BC//%,
%//AE=DF,AB=DC//%,
∴%//△AEB//%≌%//△DFC//%(%//HL//%).
【例题2】如图所示,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解:∠B+∠F=90°;理由如下:
∵∠CAB=∠EDF=90°,
BC=EF,AC=DF,
∴△ACB≌△DFE,
∴∠B=∠DEF,
∵∠DEF+∠F=90°,
∴∠B+∠F=90°.
【例题3】已知:如图,D是△ABC的BC边的中点,DE⊥AC,DF⊥AB,垂足分别为E,F.且DE=DF.
求证:△ABC是等腰三角形.
证明:∵D是△ABC的BC边的中点,
∴BD=CD,
又∵DE⊥AC,DF⊥AB,DE=DF,
∴△DFB≌△DEC,
∴∠B=∠C,∴AB=AC,
∴△ABC是等腰三角形.
1.如图,O是∠BAC内一点,且点O到AB,AC的距离OE=OF,则△AEO≌△AFO的依据是(%////%)
A.HL
B.AAS
C.SSS
D.ASA
A
2.判断下列命题的真假,并说明理由:
(1)两个锐角分别相等的两个直角三角形全等. (%////%)
(2)斜边及一锐角分别相等的两个直角三角形全等. (%////%)
(3)两条直角边分别相等的两个直角三角形全等. (%////%)
(4)一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等. (%////%)
假
真
真
真
3.如图,CD⊥AD,CB⊥AB,AB=AD .求证:CD=CB .
证明:连接AC,
∵CD⊥AD,CB⊥AB,AB=AD,
∴△ABC≌△ADC,
∴CB=CD .
4.已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,且DE=BF.
求证:(1)AE=CF; (2)AB//CD .
证明:(1)∵AB=CD,DE⊥AC,BF⊥AC,DE=BF,
∴△ABF≌△CDE,
∴AF=CE,
∴AF-EF=CE-EF,即AE=CF;
(2)由(1)得△ABF≌△CDE,
∴∠A=∠C,∴AB//CD .
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
