【五环分层导学-课件】1-8 线段的垂直平分线(2)-北师大版数学八(下)
文档属性
| 名称 | 【五环分层导学-课件】1-8 线段的垂直平分线(2)-北师大版数学八(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 11:48:33 | ||
图片预览





文档简介
(共13张PPT)
第一章 三角形的证明
第8课 线段的垂直平分线(2)
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
线段的垂直平分线定义 性质 判定
垂直于一条线段并且平分它的直线叫做这条线段的垂直平分线 线段垂直平分线上的点到这条线段两个端点的距离相等 到一条线段两个端点的距离相等的点,在这条线段的垂直平分线上
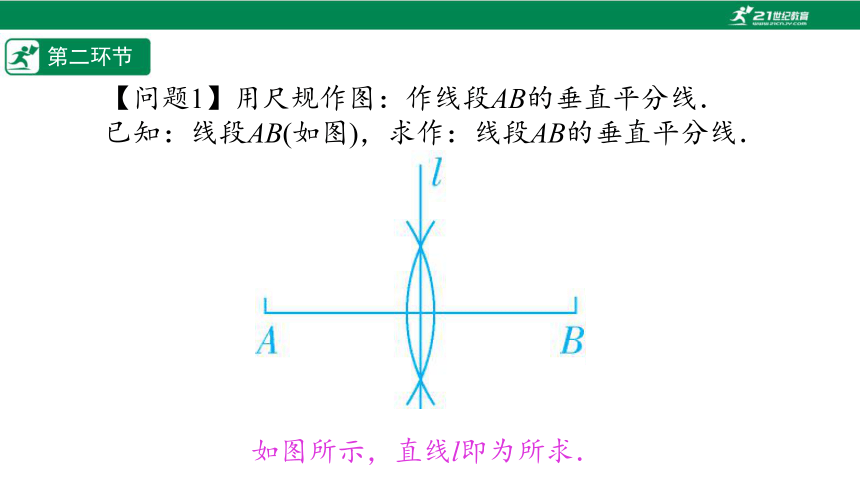
【问题1】用尺规作图:作线段AB的垂直平分线.
已知:线段AB(如图),求作:线段AB的垂直平分线.
如图所示,直线l即为所求.
【问题2】已知:底边及底边上的高,利用尺规作等腰三角形.
已知:线段a,h(如图).
求作:△ABC,使AB=AC,且BC=a,高AD=h.(不写作法和证明)
解:如图所示:
(1)作线段BC=a,
(2)作线段BC的垂直平分线MN,与线段BC
交于点D;
(3)在MN上截取DA=h,
(4)连接AB,AC,则△ABC是所求的等腰三角形.
【问题3】如图,如果点P是直线l外一点,那么怎么用尺规做l的垂线,使它经过点P呢?
答:①任取一点K,使点K与点P在直线l的两旁;
②以P为圆心,以PK长为半径画弧,交直线l于A、B两点;
③作线段AB的垂直平分线m,直线m垂直于直线l,且经过点P.
【问题4】分别作出△ABC的三边的垂直平分线.观察这三条垂直平分线,你发现了什么?
小结1:三角形三条边的垂直平分线%// //%.锐角三角形三边的垂直平分线的交点在%// //%;直角三角形三边的垂直平分线的交点在%// //%;钝角三角形三边的垂直平分线的交点在%// //%.
交于一点
三角形内
斜边的中点
三角形外
【问题5】已知:如图,在△ABC中,边AB的垂直平分线与BC的垂直平分线相交于点P.求证:边AC的垂直平分线经过点P,且PA=PB=PC .
小结2:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离%// //%.
几何语言:∵%// //% .
∴%// //%.
证明:连接PA,PB,PC,
∵边AB的垂直平分线过P点,∴PA=PB,
同理,PB=PC,∴PC=PA,
∴边AC的垂直平分线经过点P,且PA=PB=PC .
相等
点P是三角形三边垂直平分线的交点
PA=PB=PC
1.在△ABC中,AB、BC的垂直平分线交于点P,下列结论正确的是(%////%)
A.点P在AC上 B.点P在△ABC内
C.点P在在△ABC外 D.PA=PB=PC
D
2.若一个三角形两边的垂直平分线的交点在第三边上,则这个三角形是(%////%)
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
C
3.如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为%// //%.
65°
4.如图,等腰△ABC中,AB=AC,∠C=65°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是%// //%.
15°
5.(★)如图,在△ABC中,BC=2,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F,请找出图中相等的线段,并求△AEF的周长.
解:∵AB的垂直平分线交BC于点E,
∴EA=EB,
∵AC的垂直平分线交BC于点F.
∴FA=FC,
∴△AEF的周长=AE+EF+FC=BE+EF+FC=BC=2.
第一章 三角形的证明
第8课 线段的垂直平分线(2)
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
线段的垂直平分线定义 性质 判定
垂直于一条线段并且平分它的直线叫做这条线段的垂直平分线 线段垂直平分线上的点到这条线段两个端点的距离相等 到一条线段两个端点的距离相等的点,在这条线段的垂直平分线上
【问题1】用尺规作图:作线段AB的垂直平分线.
已知:线段AB(如图),求作:线段AB的垂直平分线.
如图所示,直线l即为所求.
【问题2】已知:底边及底边上的高,利用尺规作等腰三角形.
已知:线段a,h(如图).
求作:△ABC,使AB=AC,且BC=a,高AD=h.(不写作法和证明)
解:如图所示:
(1)作线段BC=a,
(2)作线段BC的垂直平分线MN,与线段BC
交于点D;
(3)在MN上截取DA=h,
(4)连接AB,AC,则△ABC是所求的等腰三角形.
【问题3】如图,如果点P是直线l外一点,那么怎么用尺规做l的垂线,使它经过点P呢?
答:①任取一点K,使点K与点P在直线l的两旁;
②以P为圆心,以PK长为半径画弧,交直线l于A、B两点;
③作线段AB的垂直平分线m,直线m垂直于直线l,且经过点P.
【问题4】分别作出△ABC的三边的垂直平分线.观察这三条垂直平分线,你发现了什么?
小结1:三角形三条边的垂直平分线%// //%.锐角三角形三边的垂直平分线的交点在%// //%;直角三角形三边的垂直平分线的交点在%// //%;钝角三角形三边的垂直平分线的交点在%// //%.
交于一点
三角形内
斜边的中点
三角形外
【问题5】已知:如图,在△ABC中,边AB的垂直平分线与BC的垂直平分线相交于点P.求证:边AC的垂直平分线经过点P,且PA=PB=PC .
小结2:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离%// //%.
几何语言:∵%// //% .
∴%// //%.
证明:连接PA,PB,PC,
∵边AB的垂直平分线过P点,∴PA=PB,
同理,PB=PC,∴PC=PA,
∴边AC的垂直平分线经过点P,且PA=PB=PC .
相等
点P是三角形三边垂直平分线的交点
PA=PB=PC
1.在△ABC中,AB、BC的垂直平分线交于点P,下列结论正确的是(%////%)
A.点P在AC上 B.点P在△ABC内
C.点P在在△ABC外 D.PA=PB=PC
D
2.若一个三角形两边的垂直平分线的交点在第三边上,则这个三角形是(%////%)
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
C
3.如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为%// //%.
65°
4.如图,等腰△ABC中,AB=AC,∠C=65°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是%// //%.
15°
5.(★)如图,在△ABC中,BC=2,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F,请找出图中相等的线段,并求△AEF的周长.
解:∵AB的垂直平分线交BC于点E,
∴EA=EB,
∵AC的垂直平分线交BC于点F.
∴FA=FC,
∴△AEF的周长=AE+EF+FC=BE+EF+FC=BC=2.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
