【五环分层导学-课件】1-11 单元复习 三角形的证明-北师大版数学八(下)
文档属性
| 名称 | 【五环分层导学-课件】1-11 单元复习 三角形的证明-北师大版数学八(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 24.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 11:48:41 | ||
图片预览






文档简介
(共46张PPT)
第一章 三角形的证明
第11课 单元复习
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】说说作为证明基础的几条基本事实.
【问题2】等腰三角形有哪些性质?等边三角形呢?直角三角形呢?它们各自分别有哪些判定条件?
【问题3】说说两个直角三角形全等的判定条件.
【问题4】分别说说线段垂直平分线,角平分线的性质定理及其逆定理.
【问题5】如何用反证法证明?请举例说明.请你说出一对互逆命题,并判断它们是真命题还是假命题.
【问题6】已知底边及底边上的高,如何用尺规作等腰三角形?已知一直角边和斜边,如何用尺规作直角三角形.
【问题7】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现全章知识结构.
考点1:等腰三角形的边角关系
【例题1】等腰三角形一腰上的高与另一腰所成的夹角为40°,则这个等腰三角形的底角为%// //%.
对点练习1:在等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为(%////%)
A.7 B.11 C.7或11 D.7或10
25°或65°
C
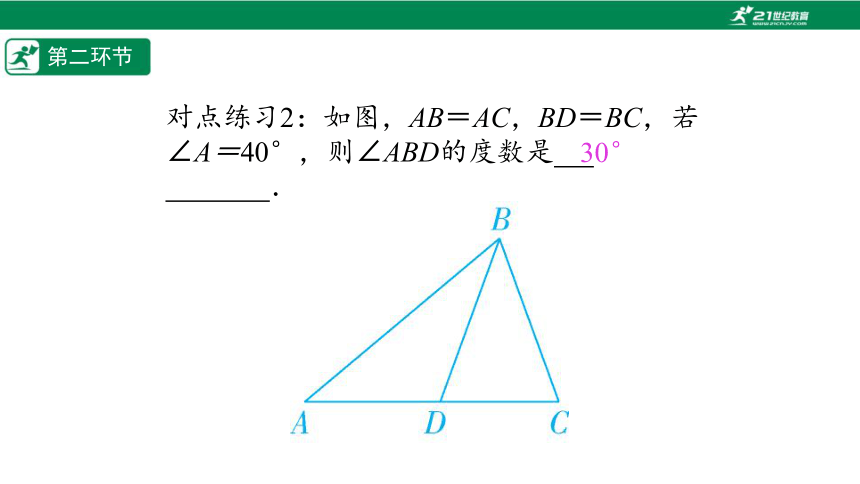
对点练习2:如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是%// //%.
30°
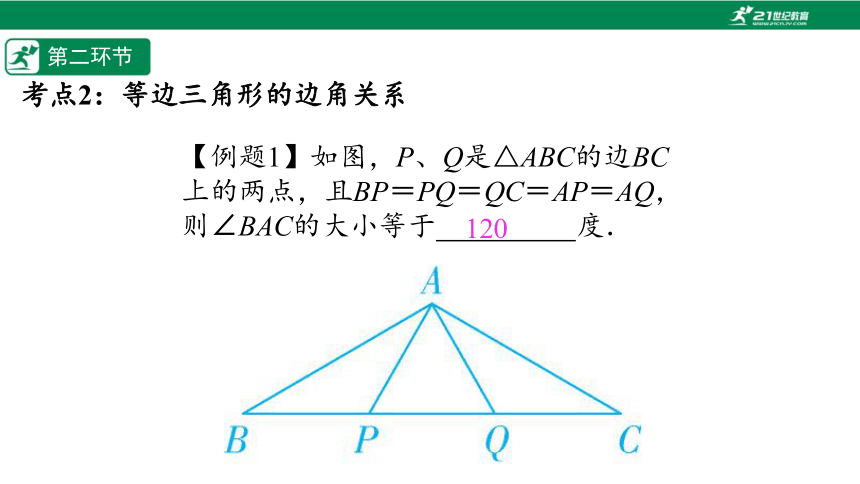
【例题1】如图,P、Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小等于%// //%度.
120
考点2:等边三角形的边角关系
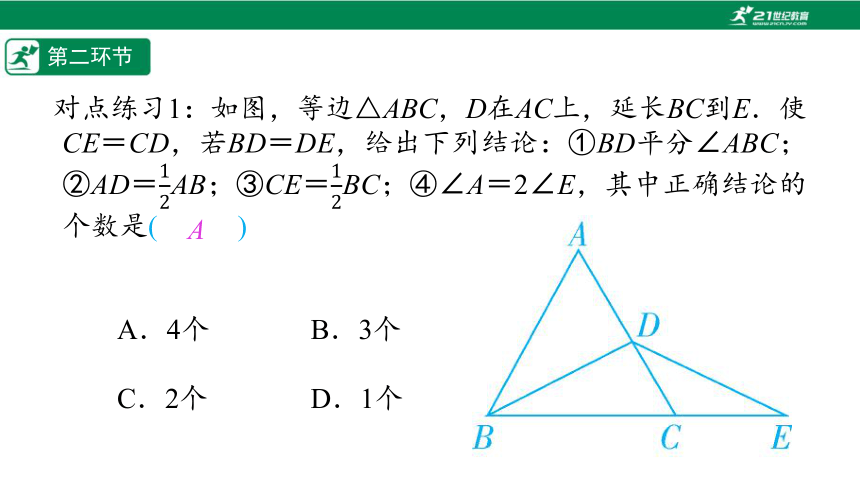
对点练习1:如图,等边△ABC,D在AC上,延长BC到E.使CE=CD,若BD=DE,给出下列结论:①BD平分∠ABC;②AD=AB;③CE=BC;④∠A=2∠E,其中正确结论的个数是(%////%)
A.4个 B.3个
C.2个 D.1个
A
【例题1】在以下列各组数为边长的三角形中,不是直角三角形的是(%////%)
A.3,4,5 B.2,2,3
C.7,24,25 D.1,,3
【例题2】在直角三角形中,如果一个锐角为30°,而斜边与较小直角边的和为12,那么斜边长为%////%.
B
8
考点3:直角三角形的边角关系
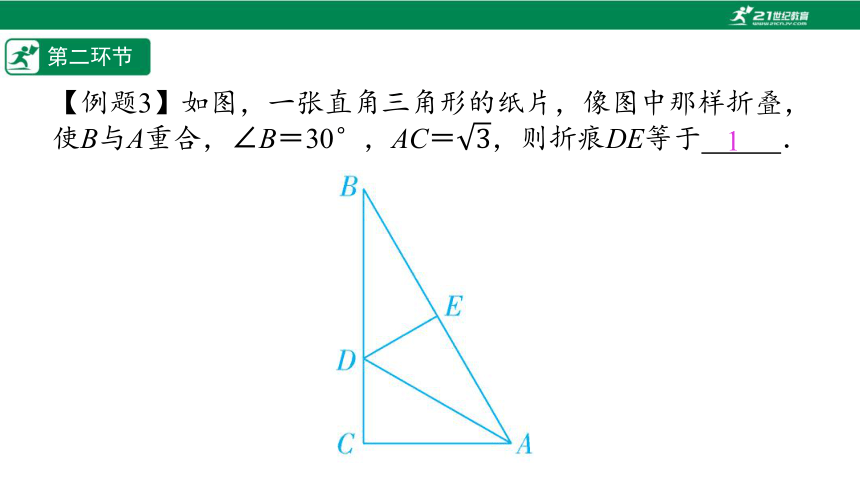
【例题3】如图,一张直角三角形的纸片,像图中那样折叠,使B与A重合,∠B=30°,AC=,则折痕DE等于%////%.
1
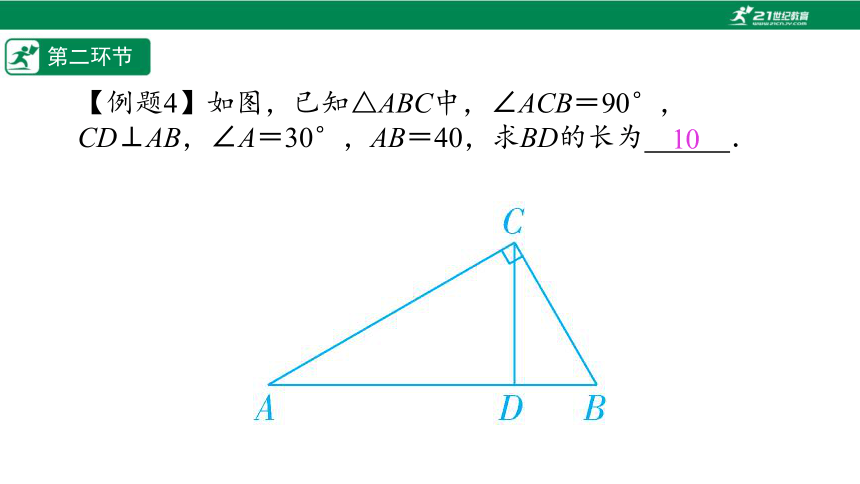
【例题4】如图,已知△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,AB=40,求BD的长为%// //%.
10
考点4:垂直平分线
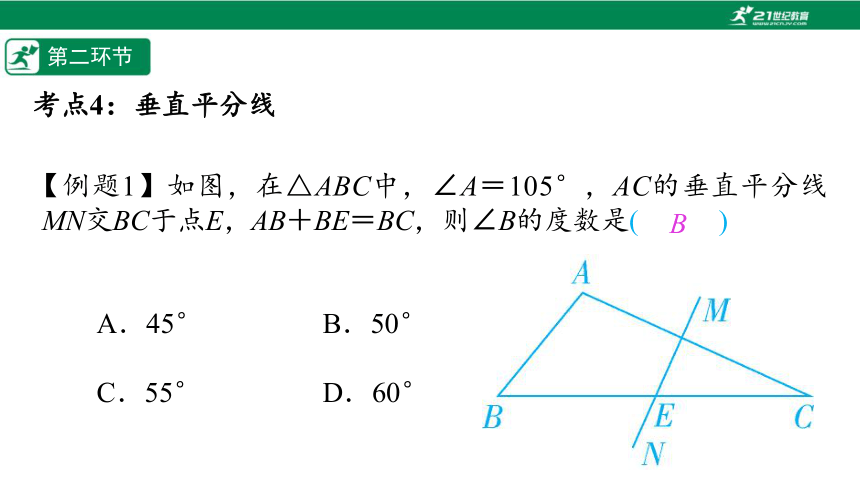
【例题1】如图,在△ABC中,∠A=105°,AC的垂直平分线MN交BC于点E,AB+BE=BC,则∠B的度数是(%////%)
A.45° B.50°
C.55° D.60°
B
对点练习1:等腰三角形一腰上的垂直平分线与这个三角形的另一边(或边所在直线)的夹角为20°,则这个等腰三角形的顶角为%// //%.
40°或70°或110°
【例题1】如图,△ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E,且AC=6 cm,则DE+BD等于%// //%.
考点5:角平分线
6 cm
对点练习1:如图,AD是△ABC的角平分线,∠C=90°,BC=9 cm,BD=5 cm,则点D到AB的距离是%// //%.
4 cm
对点练习2:如图所示,OP平分∠MON,PA⊥ON于A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为(%////%)
A.1 B.2 C.3 D.4
B
对点练习3:如图,在△ABC中,两条角平分线BD,CE交于点O,∠BOC=116°,则∠A的度数是%// //%.
对点练习4:如图,已知在△ABC中,∠B与∠C的平分线交于点P,当∠A=70°时,则∠BPC的度数为%// //%.
52°
125°
考点6:互逆命题/反证法/尺规作图
【例题1】命题:四边形是多边形.
逆命题:%// //%,原命题是%////%命题,逆命题是%////%命题.
对点练习1:下列命题中,是假命题的是(%////%)
A.斜边和一条直角边分别相等的两个直角三角形全等
B.角平分线上的点到这个角的两边的距离相等
C.有两个角相等的三角形是等腰三角形
D.有一个角是60°的三角形是等边三角形
多边形是四边形
真
假
D
【例题2】如图,已知直线l垂直平分线段AB,P是l上一点,已知PA=1,则PB=%////%.
1
对点练习2:如图,已知△ABC,按以下步骤作图:①分别以B、C为圆心,以大于BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD .若∠B=30°,∠A=55°,则∠ACD的度数为%// //%.
65°
考点7:三角形的综合
【例题1】如图,O是△ABC的∠ABC与∠ACB的平分线的交点,DE∥BC交AB于点D,交AC于点E.若AB=10 cm,AC=8 cm,则△ADE的周长是%////%cm.
18
【例题2】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.
(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
(1)证明:连接BE,∵DE是AB的垂直平分线,∴AE=BE,
∴∠ABE=∠A=30°,∴∠CBE=∠ABC-∠ABE=30°,
在Rt△ABC中,BE=2CE,∴AE=2CE;
(2)解:△BCD是等边三角形,理由如下:
∵DE垂直平分AB,∴D为AB中点,
∵∠ACB=90°,∴CD=BD,
∵∠ABC=60°,∴△BCD是等边三角形.
【例题3】如图,BD=CD,∠ABD=∠ACD=90°,点E,F分别在AB,AC上,若ED平分∠BEF,
(1)求证:FD平分∠EFC; (2)求证:EF=BE+CF.
证明:(1)如图,过D作DM⊥EF,
∵ED平分∠BEF,∴BD=DM,
∵BD=CD,∴DC=DM,∴FD平分∠EFC;
(2)∵ED平分∠BEF,∴∠BDE=∠MDE,
在△BDE和△MDE中,
∴△BDE≌△MDE(SAS),∴EB=EM,
同理CF=MF,∴EF=BE+CF.
易错点1:忽略多种情况
对点练习:等腰三角形的一个内角等于40°,则另外两个内角的度数分别为(%////%)
A.40°、100° B.70°、70°
C.70°、100° D.40°、100°或70°、70°
D
易错点2:定理不清
对点练习:到三角形三个顶点的距离相等的点是三角形 的交点.(%////%)
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高
B
1.已知△ABC的三边长分别是6 cm、8 cm、10 cm,则△ABC的面积是(%////%)
A.24 cm2 B.30 cm2 C.40 cm2 D.48 cm2
A
2.下列关于等腰三角形的性质叙述错误的是(%////%)
A.等腰三角形的两底角相等
B.等腰三角形是钝角三角形或锐角三角形
C.等腰三角形是轴对称图形
D.等腰三角形底边上的高和中线、顶角的平分线互相重合
B
3.若等腰三角形的顶角为40°,则它的底角度数为(%////%)
A.40° B.50° C.60° D.70°
D
4.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为(%////%)
A.2 B.3
C.4 D.5
C
5.如图,△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为(%////%)
A.30° B.36°
C.45° D.70°
B
6.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是(%////%)
A.1个 B.2个
C.3个 D.4个
C
7.如图,点A,C,B在同一直线上,△DAC和△EBC均是等边三角形,AE与BD交于点O,AE,BD分别与CD,CE交于点M,N,有如下结论:(1)AE=BD;(2)△ACM≌△DCN;(3)EM=BN;(4)MN∥BC;(5)∠DOA=60°.其中正确的结论有(%////%)
A.5个 B.4个
C.3个 D.2个
A
8.“等边对等角”的逆命题是%// //%.
等角对等边
9.已知△ABC中,∠ACB=90°,AC=8,BC=6,在射线BC上取一点D,使得△ABD为等腰三角形,这样的三角形有%////%个.
3
10.如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点B的坐标为(5,4),点P为BC上动点,当△POA为等腰三角形时,点P坐标为%// //%.
(2.5,4),(3,4),(2,4)
11.如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,求∠E度数.
解:∵△ABC是等边三角形,
∴∠ACB=60°,∠ACD=120°,
∵CG=CD,
∴∠CDG∠ACB=30°,∠FDE=150°,
∵DF=DE,
∴∠E∠CDG=15°.
12.如图,已知:∠AOB,点M和点N.求作:一点P,使点P到∠AOB两边的距离相等,并且满足PM=PN.
/解:如图,点P即为所求.
13.如图,△ABC中,∠B=90°,AB=BC,AD是△ABC的角平分线,若BD=1,求DC的长.
解:如图,过点D作DE⊥AC于E,
∵△ABC中,∠B=90°,
AD是△ABC的角平分线,BD=1,
∴DE=BD=1,
∵∠B=90°,AB=BC,
∴∠C=∠BAC=45°,
在Rt△DEC中,DE=EC=1,
∴由勾股定理得DC=.
14.如图,已知P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为C,D .求证:
(1)OC=OD;
(2)OP是CD的垂直平分线.
证明:(1)∵P是∠AOB平分线上的一点,
PC⊥OA,PD⊥OB,
∴PC=PD,
在Rt△POC与Rt△POD中,
∵,
∴Rt△POC≌Rt△POD(HL),∴OC=OD;
(2)∵P是∠AOB平分线上的一点,
∴∠COP=∠DOP,
∵由(1)知OC=OD,
∴在△COE与△DOE中,,
∴△COE≌△DOE,
∴CE=DE,OE⊥CD,即OP是CD的垂直平分线.
15.如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断DE与DP的位置关系,并说明理由;
(2)若AC=6,BC=8,PA=2,求线段DE的长.
/解:(1)DE⊥DP;理由如下:
∵PD=PA,∴∠A=∠PDA,
∵EF是BD的垂直平分线,
∴EB=ED,∴∠B=∠EDB,
∵∠C=90°,∴∠A+∠B=90°,
∴∠PDA+∠EDB=90°,
∴∠PDE=180°-90°=90°,∴DE⊥DP;
(2)连接PE,设DE=x,则EB=ED=x,CE=8-x,
∵∠C=∠PDE=90°,∴PC2+CE2=PE2=PD2+DE2,
∴42+(8-x)2=22+x2,解得:x=4.75,则DE=4.75.
16.(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上且CE=CA,试求∠DAE的度数;
(2)如果把第(1)题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?说明理由;
(3)如果把第(1)题中“∠BAC=90°”的条件改为“∠BAC>90°”,其余条件不变,那么∠DAE与∠BAC有怎样的大小关系?
解:(1)∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,∴∠BAD=∠BDA(180°-∠B)=67.5°,
∵CE=CA,∴∠CAE=∠E(180°-∠ACE)∠ACB=22.5°,
在△ABE中,∠BAE=180°-∠B-∠E=112.5°,
∴∠DAE=∠BAE-∠BAD=112.5°-67.5°=45°;
(2)不改变.
设∠CAE=α,∵CA=CE,∴∠E=∠CAE=α,
∴∠ACB=∠CAE+∠E=2α,
在△ABC中,∠BAC=90°,∴∠B=90°-∠ACB=90°-2α,
∵BD=BA,∴∠BAD=∠BDA(180°-∠B)=α+45°,
在△ABE中,∠BAE=180°-∠B-∠E
=180°-(90°-2α)-α=90°+α,
∴∠DAE=∠BAE-∠BAD=(90°+α)-(α+45°)=45°;
(3)∠DAE∠BAC .理由:
设∠CAE=x,∠BAD=y,
则∠B=180°-2y,∠E=∠CAE=x,
∴∠BAE=180°-∠B-∠E=2y-x,
∴∠DAE=∠BAE-∠BAD=2y-x-y=y-x,
∠BAC=∠BAE-∠CAE=2y-x-x=2y-2x,
∴∠DAE∠BAC .
第一章 三角形的证明
第11课 单元复习
北师大版八年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】说说作为证明基础的几条基本事实.
【问题2】等腰三角形有哪些性质?等边三角形呢?直角三角形呢?它们各自分别有哪些判定条件?
【问题3】说说两个直角三角形全等的判定条件.
【问题4】分别说说线段垂直平分线,角平分线的性质定理及其逆定理.
【问题5】如何用反证法证明?请举例说明.请你说出一对互逆命题,并判断它们是真命题还是假命题.
【问题6】已知底边及底边上的高,如何用尺规作等腰三角形?已知一直角边和斜边,如何用尺规作直角三角形.
【问题7】梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现全章知识结构.
考点1:等腰三角形的边角关系
【例题1】等腰三角形一腰上的高与另一腰所成的夹角为40°,则这个等腰三角形的底角为%// //%.
对点练习1:在等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为(%////%)
A.7 B.11 C.7或11 D.7或10
25°或65°
C
对点练习2:如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是%// //%.
30°
【例题1】如图,P、Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小等于%// //%度.
120
考点2:等边三角形的边角关系
对点练习1:如图,等边△ABC,D在AC上,延长BC到E.使CE=CD,若BD=DE,给出下列结论:①BD平分∠ABC;②AD=AB;③CE=BC;④∠A=2∠E,其中正确结论的个数是(%////%)
A.4个 B.3个
C.2个 D.1个
A
【例题1】在以下列各组数为边长的三角形中,不是直角三角形的是(%////%)
A.3,4,5 B.2,2,3
C.7,24,25 D.1,,3
【例题2】在直角三角形中,如果一个锐角为30°,而斜边与较小直角边的和为12,那么斜边长为%////%.
B
8
考点3:直角三角形的边角关系
【例题3】如图,一张直角三角形的纸片,像图中那样折叠,使B与A重合,∠B=30°,AC=,则折痕DE等于%////%.
1
【例题4】如图,已知△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,AB=40,求BD的长为%// //%.
10
考点4:垂直平分线
【例题1】如图,在△ABC中,∠A=105°,AC的垂直平分线MN交BC于点E,AB+BE=BC,则∠B的度数是(%////%)
A.45° B.50°
C.55° D.60°
B
对点练习1:等腰三角形一腰上的垂直平分线与这个三角形的另一边(或边所在直线)的夹角为20°,则这个等腰三角形的顶角为%// //%.
40°或70°或110°
【例题1】如图,△ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E,且AC=6 cm,则DE+BD等于%// //%.
考点5:角平分线
6 cm
对点练习1:如图,AD是△ABC的角平分线,∠C=90°,BC=9 cm,BD=5 cm,则点D到AB的距离是%// //%.
4 cm
对点练习2:如图所示,OP平分∠MON,PA⊥ON于A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为(%////%)
A.1 B.2 C.3 D.4
B
对点练习3:如图,在△ABC中,两条角平分线BD,CE交于点O,∠BOC=116°,则∠A的度数是%// //%.
对点练习4:如图,已知在△ABC中,∠B与∠C的平分线交于点P,当∠A=70°时,则∠BPC的度数为%// //%.
52°
125°
考点6:互逆命题/反证法/尺规作图
【例题1】命题:四边形是多边形.
逆命题:%// //%,原命题是%////%命题,逆命题是%////%命题.
对点练习1:下列命题中,是假命题的是(%////%)
A.斜边和一条直角边分别相等的两个直角三角形全等
B.角平分线上的点到这个角的两边的距离相等
C.有两个角相等的三角形是等腰三角形
D.有一个角是60°的三角形是等边三角形
多边形是四边形
真
假
D
【例题2】如图,已知直线l垂直平分线段AB,P是l上一点,已知PA=1,则PB=%////%.
1
对点练习2:如图,已知△ABC,按以下步骤作图:①分别以B、C为圆心,以大于BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD .若∠B=30°,∠A=55°,则∠ACD的度数为%// //%.
65°
考点7:三角形的综合
【例题1】如图,O是△ABC的∠ABC与∠ACB的平分线的交点,DE∥BC交AB于点D,交AC于点E.若AB=10 cm,AC=8 cm,则△ADE的周长是%////%cm.
18
【例题2】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.
(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
(1)证明:连接BE,∵DE是AB的垂直平分线,∴AE=BE,
∴∠ABE=∠A=30°,∴∠CBE=∠ABC-∠ABE=30°,
在Rt△ABC中,BE=2CE,∴AE=2CE;
(2)解:△BCD是等边三角形,理由如下:
∵DE垂直平分AB,∴D为AB中点,
∵∠ACB=90°,∴CD=BD,
∵∠ABC=60°,∴△BCD是等边三角形.
【例题3】如图,BD=CD,∠ABD=∠ACD=90°,点E,F分别在AB,AC上,若ED平分∠BEF,
(1)求证:FD平分∠EFC; (2)求证:EF=BE+CF.
证明:(1)如图,过D作DM⊥EF,
∵ED平分∠BEF,∴BD=DM,
∵BD=CD,∴DC=DM,∴FD平分∠EFC;
(2)∵ED平分∠BEF,∴∠BDE=∠MDE,
在△BDE和△MDE中,
∴△BDE≌△MDE(SAS),∴EB=EM,
同理CF=MF,∴EF=BE+CF.
易错点1:忽略多种情况
对点练习:等腰三角形的一个内角等于40°,则另外两个内角的度数分别为(%////%)
A.40°、100° B.70°、70°
C.70°、100° D.40°、100°或70°、70°
D
易错点2:定理不清
对点练习:到三角形三个顶点的距离相等的点是三角形 的交点.(%////%)
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高
B
1.已知△ABC的三边长分别是6 cm、8 cm、10 cm,则△ABC的面积是(%////%)
A.24 cm2 B.30 cm2 C.40 cm2 D.48 cm2
A
2.下列关于等腰三角形的性质叙述错误的是(%////%)
A.等腰三角形的两底角相等
B.等腰三角形是钝角三角形或锐角三角形
C.等腰三角形是轴对称图形
D.等腰三角形底边上的高和中线、顶角的平分线互相重合
B
3.若等腰三角形的顶角为40°,则它的底角度数为(%////%)
A.40° B.50° C.60° D.70°
D
4.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为(%////%)
A.2 B.3
C.4 D.5
C
5.如图,△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为(%////%)
A.30° B.36°
C.45° D.70°
B
6.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是(%////%)
A.1个 B.2个
C.3个 D.4个
C
7.如图,点A,C,B在同一直线上,△DAC和△EBC均是等边三角形,AE与BD交于点O,AE,BD分别与CD,CE交于点M,N,有如下结论:(1)AE=BD;(2)△ACM≌△DCN;(3)EM=BN;(4)MN∥BC;(5)∠DOA=60°.其中正确的结论有(%////%)
A.5个 B.4个
C.3个 D.2个
A
8.“等边对等角”的逆命题是%// //%.
等角对等边
9.已知△ABC中,∠ACB=90°,AC=8,BC=6,在射线BC上取一点D,使得△ABD为等腰三角形,这样的三角形有%////%个.
3
10.如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点B的坐标为(5,4),点P为BC上动点,当△POA为等腰三角形时,点P坐标为%// //%.
(2.5,4),(3,4),(2,4)
11.如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,求∠E度数.
解:∵△ABC是等边三角形,
∴∠ACB=60°,∠ACD=120°,
∵CG=CD,
∴∠CDG∠ACB=30°,∠FDE=150°,
∵DF=DE,
∴∠E∠CDG=15°.
12.如图,已知:∠AOB,点M和点N.求作:一点P,使点P到∠AOB两边的距离相等,并且满足PM=PN.
/解:如图,点P即为所求.
13.如图,△ABC中,∠B=90°,AB=BC,AD是△ABC的角平分线,若BD=1,求DC的长.
解:如图,过点D作DE⊥AC于E,
∵△ABC中,∠B=90°,
AD是△ABC的角平分线,BD=1,
∴DE=BD=1,
∵∠B=90°,AB=BC,
∴∠C=∠BAC=45°,
在Rt△DEC中,DE=EC=1,
∴由勾股定理得DC=.
14.如图,已知P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为C,D .求证:
(1)OC=OD;
(2)OP是CD的垂直平分线.
证明:(1)∵P是∠AOB平分线上的一点,
PC⊥OA,PD⊥OB,
∴PC=PD,
在Rt△POC与Rt△POD中,
∵,
∴Rt△POC≌Rt△POD(HL),∴OC=OD;
(2)∵P是∠AOB平分线上的一点,
∴∠COP=∠DOP,
∵由(1)知OC=OD,
∴在△COE与△DOE中,,
∴△COE≌△DOE,
∴CE=DE,OE⊥CD,即OP是CD的垂直平分线.
15.如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断DE与DP的位置关系,并说明理由;
(2)若AC=6,BC=8,PA=2,求线段DE的长.
/解:(1)DE⊥DP;理由如下:
∵PD=PA,∴∠A=∠PDA,
∵EF是BD的垂直平分线,
∴EB=ED,∴∠B=∠EDB,
∵∠C=90°,∴∠A+∠B=90°,
∴∠PDA+∠EDB=90°,
∴∠PDE=180°-90°=90°,∴DE⊥DP;
(2)连接PE,设DE=x,则EB=ED=x,CE=8-x,
∵∠C=∠PDE=90°,∴PC2+CE2=PE2=PD2+DE2,
∴42+(8-x)2=22+x2,解得:x=4.75,则DE=4.75.
16.(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上且CE=CA,试求∠DAE的度数;
(2)如果把第(1)题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?说明理由;
(3)如果把第(1)题中“∠BAC=90°”的条件改为“∠BAC>90°”,其余条件不变,那么∠DAE与∠BAC有怎样的大小关系?
解:(1)∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,∴∠BAD=∠BDA(180°-∠B)=67.5°,
∵CE=CA,∴∠CAE=∠E(180°-∠ACE)∠ACB=22.5°,
在△ABE中,∠BAE=180°-∠B-∠E=112.5°,
∴∠DAE=∠BAE-∠BAD=112.5°-67.5°=45°;
(2)不改变.
设∠CAE=α,∵CA=CE,∴∠E=∠CAE=α,
∴∠ACB=∠CAE+∠E=2α,
在△ABC中,∠BAC=90°,∴∠B=90°-∠ACB=90°-2α,
∵BD=BA,∴∠BAD=∠BDA(180°-∠B)=α+45°,
在△ABE中,∠BAE=180°-∠B-∠E
=180°-(90°-2α)-α=90°+α,
∴∠DAE=∠BAE-∠BAD=(90°+α)-(α+45°)=45°;
(3)∠DAE∠BAC .理由:
设∠CAE=x,∠BAD=y,
则∠B=180°-2y,∠E=∠CAE=x,
∴∠BAE=180°-∠B-∠E=2y-x,
∴∠DAE=∠BAE-∠BAD=2y-x-y=y-x,
∠BAC=∠BAE-∠CAE=2y-x-x=2y-2x,
∴∠DAE∠BAC .
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
