2023—2024学年人教版数学七年级下册第5章相交线与平行线单元同步检测试题(含答案)
文档属性
| 名称 | 2023—2024学年人教版数学七年级下册第5章相交线与平行线单元同步检测试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 586.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 00:00:00 | ||
图片预览



文档简介
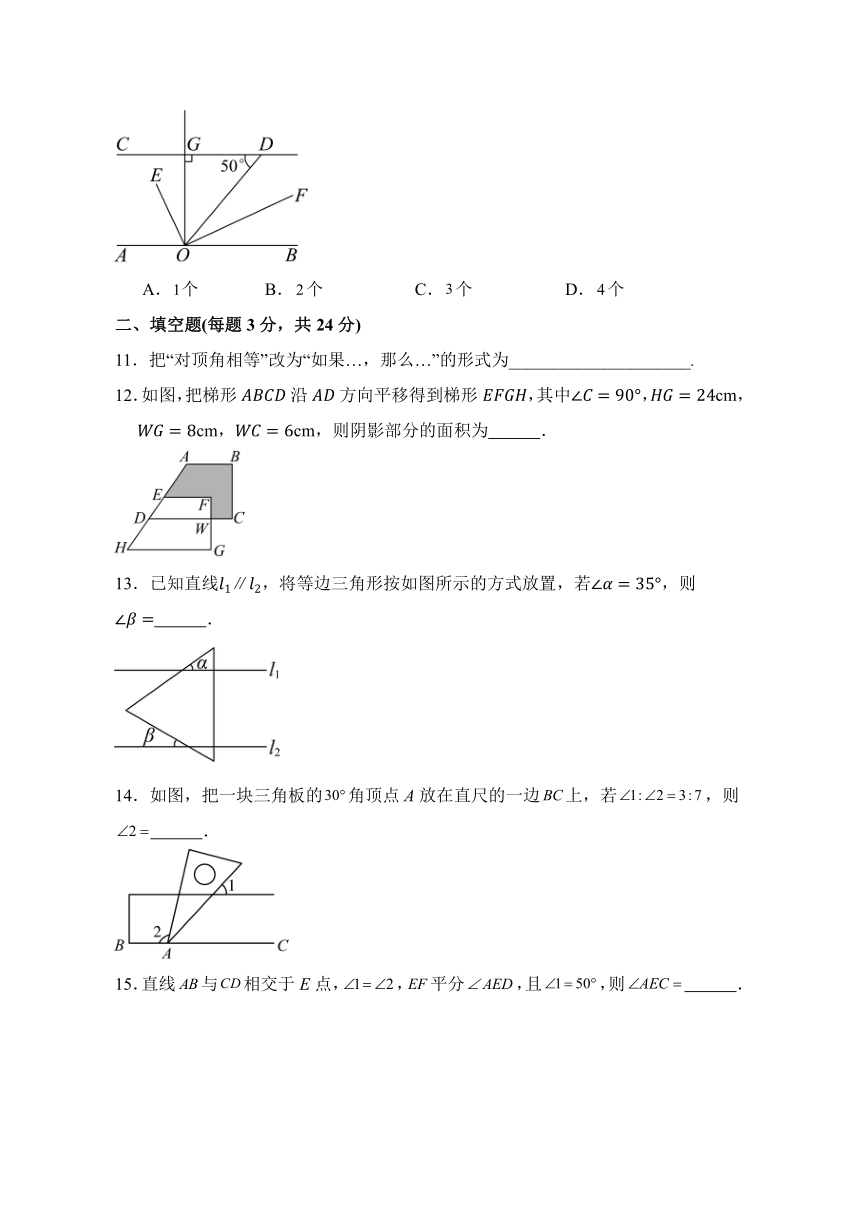
第五章《相交线与平行线》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下列现象中,属于平移的是( )
A.滚动的足球 B.转动的电风扇叶片
C.正在上升的电梯 D.正在行驶的汽车后轮
2.下列图形中,线段AD的长度表示点A到直线BC距离的是( )
A.B. C.D.
3.下列命题中,是真命题的是( )
A.同位角相等 B.同旁内角互补 C.内错角相等 D.对顶角相等
4.如图,下列条件中,不能判断直线a∥b的是( )
A.∠2=∠3 B.∠2=∠5 C.∠1=∠3 D.∠2+∠4=180°
5.下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行
B.对顶角一定相等
C.直线外一点到这条直线的垂线段,叫做点到直线的距离
D.互补的两个角是邻补角
6.如图,直线,直线,若, 则( )
A.30° B.40° C.50° D.60°
7.如图,一条街道有两个拐角和,已知,若,则的度数是( )
A. B. C. D.
8.如图,△ABC平移到△DEF的位置,则下列说法:①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C到点F的方向;④平移距离为线段BD的长.其中说法正确的有( )
A.①② B.①③ C.①④ D.②④
9.我市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=50°,当∠MAC为( )度时,AM∥BE.
A.15 B.65 C.70 D.115
10.如图,,平分,,,,则下列结论:①;②平分;③;④.其中正确结论的个数是( )
A.个 B.个 C.个 D.个
二、填空题(每题3分,共24分)
11.把“对顶角相等”改为“如果…,那么…”的形式为_____________________.
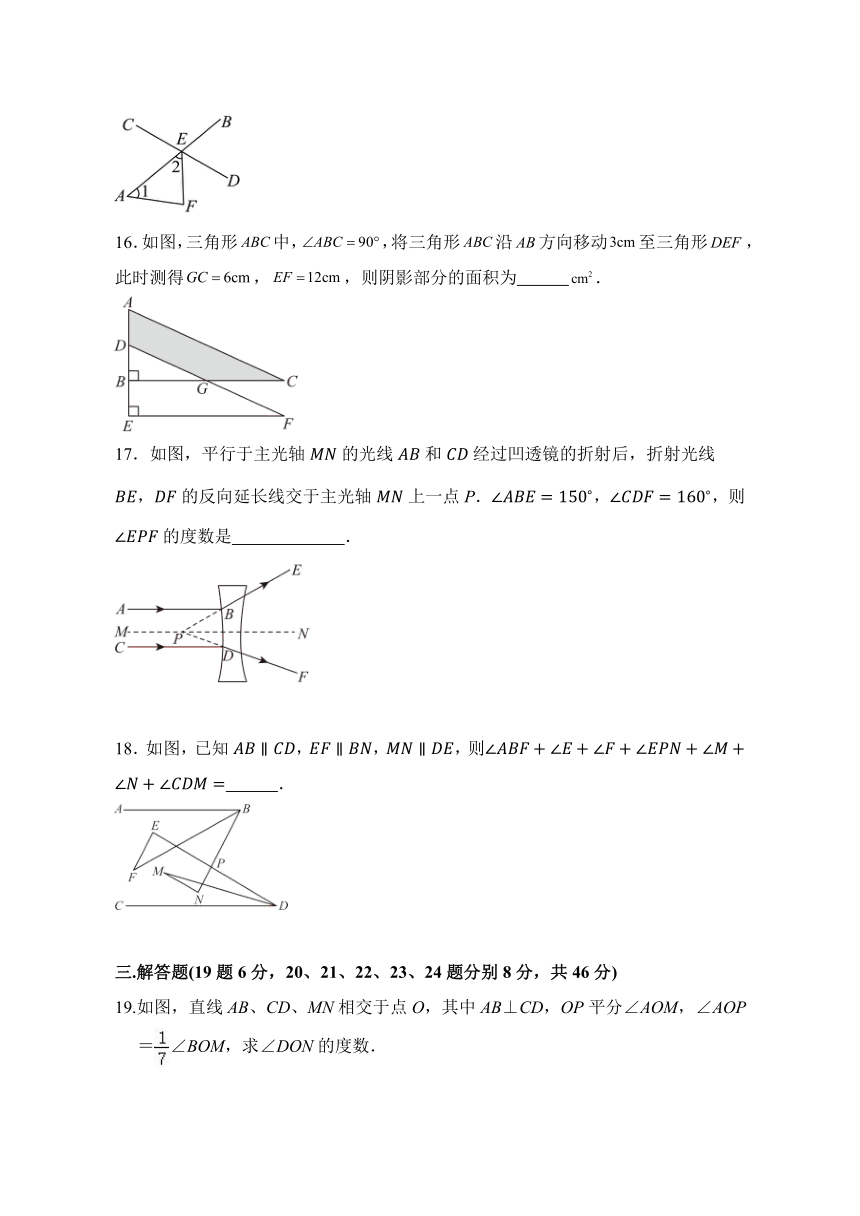
12.如图,把梯形沿方向平移得到梯形,其中,,,,则阴影部分的面积为 .
13.已知直线,将等边三角形按如图所示的方式放置,若,则 .
14.如图,把一块三角板的角顶点A放在直尺的一边上,若,则 .
15.直线与相交于E点,,平分,且,则 .
16.如图,三角形中,,将三角形沿方向移动至三角形,此时测得,,则阴影部分的面积为 .
17.如图,平行于主光轴的光线和经过凹透镜的折射后,折射光线的反向延长线交于主光轴上一点P.,,则的度数是 .
18.如图,已知,,,则 .
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.如图,直线AB、CD、MN相交于点O,其中AB⊥CD,OP平分∠AOM,∠AOP=∠BOM,求∠DON的度数.
20.如图,∠4+∠ADC=180°,且∠1=∠2,说明DG∥AB的理由.
21.(8分)如图,已知AB∥CD,试再添加一个条件,使∠1=∠2成立.
(1)写出两个不同的条件;
(2)从(1)中选择一个来证明.
22.(8分)如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
23.如图1,点E、F分别在直线、上,的平分线交于G,且.
(1)判断直线与直线的位置关系,并说明理由;
(2)如图2,点H在射线上,的平分线交于K.
①当时,求的度数;
②若,求证:.
24.阅读下列材料:
如图,,,分别是,上的点,点在,之间,连接,我们可以通过作辅助线证明结论:.
请你利用这个结论或证明思路,完成下列问题.
已知,,分别是,上的点,点在,之间,连接,.
(1)如图,若,,请直接写出的度数;
(2)如图,与的平分线交于点,用等式表示与的数量关系,并证明;
(3)如图,与的平分线交于点,直接用等式表示与的数量关系.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D A B D A B C B
二、填空题:
11..如果两个角互为对顶角,那么这两个角相等.
12.解:∵梯形沿方向平移得到梯形,
∴,,
∴,即,
∵,
∴,
∴,
故答案为:.
13.解:过点B作,
∴
∵是等边三角形,
∴
∴
∵,
∴
∴
故答案为:
14./105度
15./80度
16.18
17.故答案为:.
18.故答案为:.
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.解:设∠AOP=x°,
∵∠AOP=∠BOM,
∴∠BOM=7∠AOP=7x°,
∵OP平分∠AOM,
∴∠AOM=2∠AOP=2x°,
∵∠AOM+∠BOM=180°,
∴2x+7x=180,
解得:x=20,
∴∠AOM=2x°=40°,
∵AB⊥CD,
∴∠AOD=90°,
∴∠DON=180°﹣∠AOM﹣∠AOD=50°,
∴∠DON的度数为50°.
20.解:∵∠4+∠ADC=180°,∠4+∠5=180° (平角定义),
∴∠5=∠ADC,
∴EF∥AD,
∴∠1=∠3,
∵∠1=∠2,
∴∠3=∠2,
∴DG∥AB.
21.解:此题答案不唯一,合理即可.
(1)添加∠FCB=∠CBE或CF∥BE.
(2)已知AB∥CD,CF∥BE.求证:∠1=∠2.
证明:∵AB∥CD,∴∠DCB=∠ABC.
∵CF∥BE,∴∠FCB=∠CBE,
∴∠DCB-∠FCB=∠ABC-∠CBE,即∠1=∠2.
22.解:(1)DE∥BC,理由如下:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,
∴AB∥EF,
∴∠3=∠5,
∵∠3=∠B,
∴∠5=∠B,
∴DE∥BC,
(2)∵DE平分∠ADC,
∴∠5=∠6,
∵DE∥BC,
∴∠5=∠B,
∵∠2=3∠B,
∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,
∴∠B=36°,
∴∠2=108°,
∵∠1+∠2=180°,
∴∠1=72°.
23.(1),理由见详解
(2)①;②见详解
【分析】(1)根据角平分线的性质得,由,所以,根据平行线的判定得;
(2)①根据平行线的性质得,所以,根据角平分线的性质得,,所以;
②根据垂线的定义得,所以,根据等角的余角相等得,根据平行线的性质得,所以,即可得出结论.
【详解】(1)解:,
理由:∵平分,
∴,
∵,
∴,
∴;
(2)①解:∵,
∴°,
∴,
∵平分,平分,
∴,,
∴;
②证明:∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴.
【点睛】本题考查了平行线的判定和性质,垂线的定义以及角平分线的定义,解答的关键是结合图形分析清楚角与角之间的关系.
24.(1)
(2)
(3)
【分析】(1)根据题意可知,,可得,从而可得答案;
(2)由(1)同理可得:,,再证明,,从而可得答案;
(3)由(1)同理可得:,,再证明,从而可得结论.
【详解】(1)解:由题意知,,
,,
.
.
(2)解:由(1)同理可得,,
与的平分线交于点,
,,
.
∴.
(3)解:由(1)同理可得,,
与的平分线交于点,
,,
,
.
∴.
【点睛】本题考查的是平行线的性质,角平分线的定义,作出合适的辅助线是解本题的关键.
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下列现象中,属于平移的是( )
A.滚动的足球 B.转动的电风扇叶片
C.正在上升的电梯 D.正在行驶的汽车后轮
2.下列图形中,线段AD的长度表示点A到直线BC距离的是( )
A.B. C.D.
3.下列命题中,是真命题的是( )
A.同位角相等 B.同旁内角互补 C.内错角相等 D.对顶角相等
4.如图,下列条件中,不能判断直线a∥b的是( )
A.∠2=∠3 B.∠2=∠5 C.∠1=∠3 D.∠2+∠4=180°
5.下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行
B.对顶角一定相等
C.直线外一点到这条直线的垂线段,叫做点到直线的距离
D.互补的两个角是邻补角
6.如图,直线,直线,若, 则( )
A.30° B.40° C.50° D.60°
7.如图,一条街道有两个拐角和,已知,若,则的度数是( )
A. B. C. D.
8.如图,△ABC平移到△DEF的位置,则下列说法:①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C到点F的方向;④平移距离为线段BD的长.其中说法正确的有( )
A.①② B.①③ C.①④ D.②④
9.我市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=50°,当∠MAC为( )度时,AM∥BE.
A.15 B.65 C.70 D.115
10.如图,,平分,,,,则下列结论:①;②平分;③;④.其中正确结论的个数是( )
A.个 B.个 C.个 D.个
二、填空题(每题3分,共24分)
11.把“对顶角相等”改为“如果…,那么…”的形式为_____________________.
12.如图,把梯形沿方向平移得到梯形,其中,,,,则阴影部分的面积为 .
13.已知直线,将等边三角形按如图所示的方式放置,若,则 .
14.如图,把一块三角板的角顶点A放在直尺的一边上,若,则 .
15.直线与相交于E点,,平分,且,则 .
16.如图,三角形中,,将三角形沿方向移动至三角形,此时测得,,则阴影部分的面积为 .
17.如图,平行于主光轴的光线和经过凹透镜的折射后,折射光线的反向延长线交于主光轴上一点P.,,则的度数是 .
18.如图,已知,,,则 .
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.如图,直线AB、CD、MN相交于点O,其中AB⊥CD,OP平分∠AOM,∠AOP=∠BOM,求∠DON的度数.
20.如图,∠4+∠ADC=180°,且∠1=∠2,说明DG∥AB的理由.
21.(8分)如图,已知AB∥CD,试再添加一个条件,使∠1=∠2成立.
(1)写出两个不同的条件;
(2)从(1)中选择一个来证明.
22.(8分)如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
23.如图1,点E、F分别在直线、上,的平分线交于G,且.
(1)判断直线与直线的位置关系,并说明理由;
(2)如图2,点H在射线上,的平分线交于K.
①当时,求的度数;
②若,求证:.
24.阅读下列材料:
如图,,,分别是,上的点,点在,之间,连接,我们可以通过作辅助线证明结论:.
请你利用这个结论或证明思路,完成下列问题.
已知,,分别是,上的点,点在,之间,连接,.
(1)如图,若,,请直接写出的度数;
(2)如图,与的平分线交于点,用等式表示与的数量关系,并证明;
(3)如图,与的平分线交于点,直接用等式表示与的数量关系.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D A B D A B C B
二、填空题:
11..如果两个角互为对顶角,那么这两个角相等.
12.解:∵梯形沿方向平移得到梯形,
∴,,
∴,即,
∵,
∴,
∴,
故答案为:.
13.解:过点B作,
∴
∵是等边三角形,
∴
∴
∵,
∴
∴
故答案为:
14./105度
15./80度
16.18
17.故答案为:.
18.故答案为:.
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.解:设∠AOP=x°,
∵∠AOP=∠BOM,
∴∠BOM=7∠AOP=7x°,
∵OP平分∠AOM,
∴∠AOM=2∠AOP=2x°,
∵∠AOM+∠BOM=180°,
∴2x+7x=180,
解得:x=20,
∴∠AOM=2x°=40°,
∵AB⊥CD,
∴∠AOD=90°,
∴∠DON=180°﹣∠AOM﹣∠AOD=50°,
∴∠DON的度数为50°.
20.解:∵∠4+∠ADC=180°,∠4+∠5=180° (平角定义),
∴∠5=∠ADC,
∴EF∥AD,
∴∠1=∠3,
∵∠1=∠2,
∴∠3=∠2,
∴DG∥AB.
21.解:此题答案不唯一,合理即可.
(1)添加∠FCB=∠CBE或CF∥BE.
(2)已知AB∥CD,CF∥BE.求证:∠1=∠2.
证明:∵AB∥CD,∴∠DCB=∠ABC.
∵CF∥BE,∴∠FCB=∠CBE,
∴∠DCB-∠FCB=∠ABC-∠CBE,即∠1=∠2.
22.解:(1)DE∥BC,理由如下:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,
∴AB∥EF,
∴∠3=∠5,
∵∠3=∠B,
∴∠5=∠B,
∴DE∥BC,
(2)∵DE平分∠ADC,
∴∠5=∠6,
∵DE∥BC,
∴∠5=∠B,
∵∠2=3∠B,
∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,
∴∠B=36°,
∴∠2=108°,
∵∠1+∠2=180°,
∴∠1=72°.
23.(1),理由见详解
(2)①;②见详解
【分析】(1)根据角平分线的性质得,由,所以,根据平行线的判定得;
(2)①根据平行线的性质得,所以,根据角平分线的性质得,,所以;
②根据垂线的定义得,所以,根据等角的余角相等得,根据平行线的性质得,所以,即可得出结论.
【详解】(1)解:,
理由:∵平分,
∴,
∵,
∴,
∴;
(2)①解:∵,
∴°,
∴,
∵平分,平分,
∴,,
∴;
②证明:∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴.
【点睛】本题考查了平行线的判定和性质,垂线的定义以及角平分线的定义,解答的关键是结合图形分析清楚角与角之间的关系.
24.(1)
(2)
(3)
【分析】(1)根据题意可知,,可得,从而可得答案;
(2)由(1)同理可得:,,再证明,,从而可得答案;
(3)由(1)同理可得:,,再证明,从而可得结论.
【详解】(1)解:由题意知,,
,,
.
.
(2)解:由(1)同理可得,,
与的平分线交于点,
,,
.
∴.
(3)解:由(1)同理可得,,
与的平分线交于点,
,,
,
.
∴.
【点睛】本题考查的是平行线的性质,角平分线的定义,作出合适的辅助线是解本题的关键.
