冀教版八年级数学下册第二十二章四边形单元复习题(含解析)
文档属性
| 名称 | 冀教版八年级数学下册第二十二章四边形单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 485.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 15:08:30 | ||
图片预览




文档简介
冀教版八年级数学下册第二十二章四边形单元复习题
一、单选题
1.下列哪个度数不可能是一个多边形的内角和( )
A. B. C. D.
2.平行四边形ABCD中,∠A=50°,则∠B的度数是( )
A.40° B.50° C.130° D.150°
3.如图,在中,,点为垂足,如果,则( )
A. B. C. D.
4.若菱形的两条对角线长分别为8和6,则这个菱形的面积是( )
A.96 B.48 C.24 D.12
5.下列命题为真命题的是( )
A.菱形的四个角相等 B.菱形的对角线相等
C.菱形的四条边互相垂直 D.菱形是轴对称图形
6.下列命题的逆命题正确的是( )
A.平行四边形的两组对边分别平行
B.对顶角相等
C.矩形是平行四边形
D.全等三角形的对应角相等
7.如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.
A.45 B.46 C.47 D.48
8.如图,在中,,,为斜边上一动点,,,垂足分别为、.则线段的最小值为
A. B. C. D.
9.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D同时出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,当四边形ABPQ初次为矩形时,点P和点Q运动的时间为( )秒.
A.2 B.3 C.4 D.5
10.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A.AC=BD B.BC=CD C.AD=BC D.AB=CD
二、填空题
11.如图,在△ABC中,D,E分别是AB,AC的中点.若BC=12,则DE的长为 .
12.一个多边形的每一个内角为108°,则这个多边形是 边形,它的内角和是
13.如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有 .(填序号)
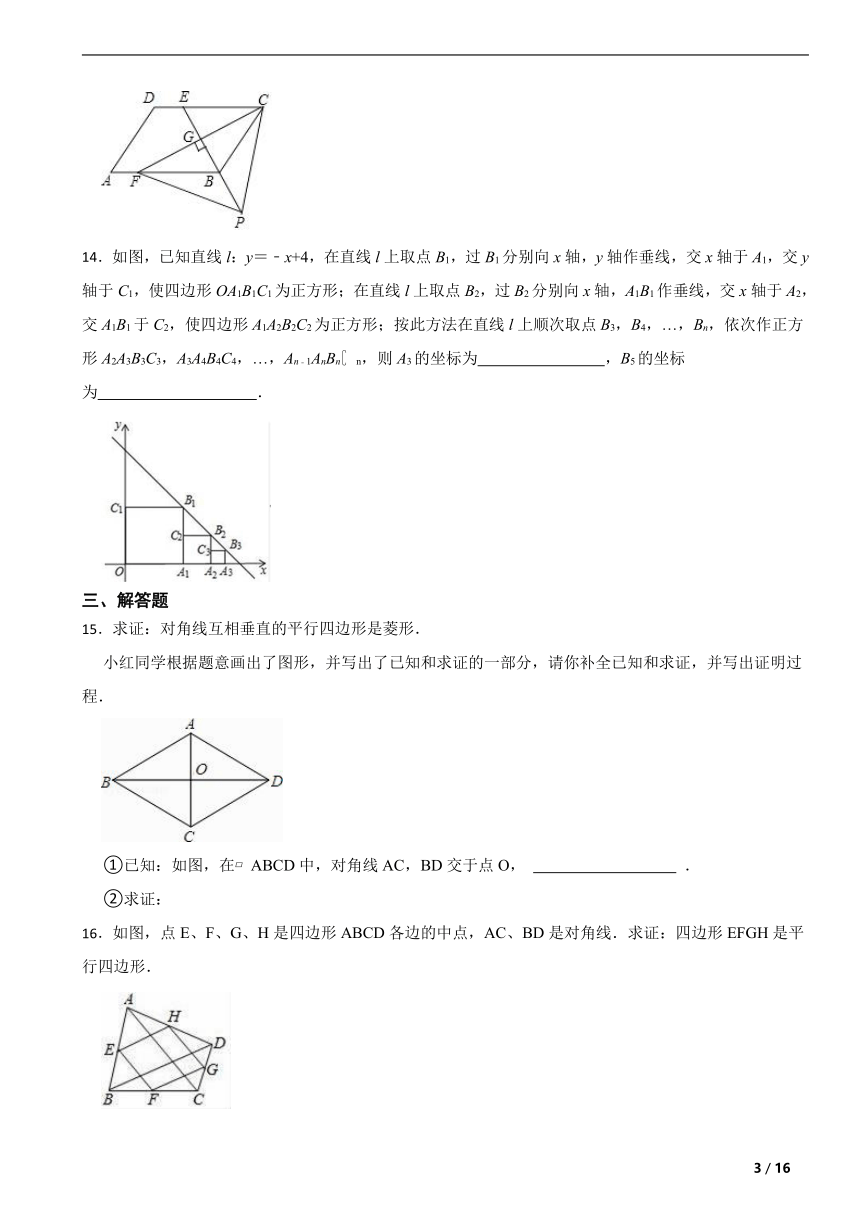
14.如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBn n,则A3的坐标为 ,B5的坐标为 .
三、解答题
15.求证:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.
①已知:如图,在 ABCD中,对角线AC,BD交于点O, .
②求证:
16.如图,点E、F、G、H是四边形ABCD各边的中点,AC、BD是对角线.求证:四边形EFGH是平行四边形.
17.(1)在数学活动课上,老师要求同学利用手中纸片剪出一块面积为的正方形,试求出这个正方形的边长.
(2)小强的手中有两块边长都为的正方形纸片,他想将这两块正方形纸片沿对角线剪开,拼成如图所示的一个大正方形,请求出这个大正方形的面积.它的边长是整数吗 若不是整数,那么请你估计这个边长的值在哪两个整数之间.
18.如图,点E,F分别在菱形ABCD的边BC,CD上,且BE=DF.求证:∠BAE=∠DAF.
19.如图,在 ABCD中,对角线AC,BD相交于点O,BE⊥AC于点E,CF⊥BD于点F,BE CF.
(1)求证: ABCD是矩形.
(2)若OD=13,CF=12,求BF的长.
20.如图,在 中,点O是AC边的一个动点,过点O作 ,交 的平分线于点E,交 的外角平分线于点F,
(1)求证: ;
(2)当点O位于AC边的什么位置时四边形AECF是矩形?并说明理由.
21.如图,在△ABC中,AC=BC,E是AB上一点,且CE=BE,将△CBE绕点C旋转得到△CAD.
(1)求证:AB∥DC;
(2)连接DE,判断四边形BEDC的形状,并说明理由.
22.如图,四边形中,,点O为对角线的中点,过点O的直线l分别与、所在的直线相交于点E、F.(点E不与点D重合)
(1)求证:;
(2)当直线时,连接、,试判断四边形的形状,并说明理由.
23.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
答案解析部分
1.【答案】B
【解析】【解答】解:n边形的内角和为(n-2)×180°,故内角和为180°的倍数.
∵360°=2×180°,900°=5×180°,1800°=10×180°,
∴600°不可能是一个多边形的内角和.
故答案为:B.
【分析】n边形的内角和为(n-2)×180°,故内角和为180°的倍数,据此判断.
2.【答案】C
【解析】【解答】∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A=50°,
∴∠B=130°,
故答案为:C.
【分析】根据平行四边形的性质解决问题即可.
3.【答案】B
【解析】【解答】解:在 ABCD中,∠D=55°,
∴∠D=55°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠BCE=90°-∠B=35°.
故答案为:B.
【分析】由平行四边形的对角相等可得∠B,又由CE⊥AB,即可求得∠BCE的度数.
4.【答案】C
【解析】【解答】解:∵四边形ABCD是菱形,
∴S= ×6×8=24.
故答案为:C.
【分析】根据菱形的面积等于对角线乘积的一半计算即可.
5.【答案】D
【解析】【解答】解:A、菱形的四个角不一定相等,故错误,是假命题,不符合题意;
B、菱形的对角线互相垂直但不一定相等,故错误,是假命题,不符合题意;
C、菱形的四条边相等但不一定互相垂直,故错误,是假命题,不符合题意;
D、菱形是轴对称图形,正确,是真命题,符合题意.
故答案为:D.
【分析】A、矩形的四个角都相等,菱形的四个角不一定相等;
B、由菱形的性质可知:菱形的对角线互相垂直;
C、由菱形的性质可知:菱形的四条边相等;
D、由菱形的性质可知:菱形是轴对称图形.
6.【答案】A
【解析】【解答】解:A、逆命题:两组对边分别平行的四边形是平行四边形,逆命题正确,故符合题意;
B、逆命题:相等的角是对顶角,逆命题错误,故不符合题意;
C、逆命题:平行四边形是矩形,逆命题错误,故不符合题意;
D、逆命题:对应角相等的三角形全等,逆命题错误,故不符合题意;
故答案为:A.
【分析】分别写出各项中命题的逆命题,再判断真假即可.
7.【答案】D
【解析】【解答】解:作GM⊥EF于点M,如图所示:
由题意得:S⑤=S四边形ABCD﹣ (S①+S②+S③+S④)=4cm2,
∴S菱形EFGH=14+4=18cm2,
又∵∠F=30°,
设菱形的边长为x,则菱形的高为:GM=GF=vx,
根据菱形的面积公式得:x x=18,
解得:x=6,
∴菱形的边长为6cm,
而①②③④四个平行四边形周长的总和=2(AE+AH+HD+DG+GC+CF+FB+BE)=2(EF+FG+GH+HE)=48cm.
故选:D.
【分析】根据①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,可求出⑤的面积,从而可求出菱形的面积,根据菱形的性质可求出边长,进而可求出①②③④四个平行四边形周长的总和.
8.【答案】D
【解析】【解答】解:如图,连接CD,
,,,
四边形CEDF是矩形,
,
由垂线段最短可得CD⊥AB时线段EF的长最小,
,,
,
四边形CEDF是矩形,
.
故答案为:D.
【分析】连接CD,则四边形CEDF是矩形,EF=CD,由垂线段最短可得CD⊥AB时线段EF的长最小,利用勾股定理可得AB,然后根据等面积法可得CD,据此解答.
9.【答案】C
【解析】【解答】解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20-2x.
解得x=4,
故答案为:C.
【分析】设最快x秒,根据题意列出方程3x=20-2x,再求出x的值即可。
10.【答案】B
【解析】【分析】根据四边形ABCD中,∠A=∠B=∠C=90°,得出四边形ABCD是矩形,进而利用正方形的判定定理得出需要添加的条件.
【解答】∵四边形ABCD中,∠A=∠B=∠C=90°,
∴四边形ABCD是矩形,
当一组邻边相等时,矩形ABCD为正方形,
这个条件可以是:BC=DC.
故选B.
【点评】此题主要考查了正方形的判定,根据矩形的判定性质得出四边形ABCD是矩形是解决问题的关键.
11.【答案】6
【解析】【解答】解:∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
又BC=12,
∴
故答案为:6.
【分析】由题意可得DE是△ABC的中位线,则DE=BC,据此计算.
12.【答案】五;540°
【解析】【解答】解:∵多边形的每一个内角都等于108°,
∴多边形的每一个外角都等于180°﹣108°=72°,
∴边数n=360°÷72°=5,
内角和为(5﹣2)×180°=540°.
故答案为:五;540°.
【分析】先求出这个多边形的每一个外角的度数,再用360°除以一个外角的度数即可得到边数.
13.【答案】①②③④
【解析】【解答】解:证明:∵BC=EC,
∴∠CEB=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CEB=∠EBF,
∴∠CBE=∠EBF,
∴①BE平分∠CBF,正确;
∵BC=EC,CF⊥BE,
∴∠ECF=∠BCF,
∴②CF平分∠DCB,正确;
∵DC∥AB,
∴∠DCF=∠CFB,
∵∠ECF=∠BCF,
∴∠CFB=∠BCF,
∴BF=BC,
∴③正确;
∵FB=BC,CF⊥BE,
∴B点一定在FC的垂直平分线上,即PB垂直平分FC,
∴PF=PC,故④正确.
故答案为①②③④.
【分析】分别利用平行线的性质结合线段垂直平分线的性质以及等腰三角形的性质分别判断得出答案.
14.【答案】( ,0);( , )
【解析】【解答】解:当x=0,y=4,当y=0时,﹣x+4=0,x=4,
∴OE=OF=4,
∴△EOF是等腰直角三角形,
∴∠C1EF=45°
∴△B1C1E是等腰直角三角形,
∴B1C1=EC1,
∵四边形OA1B1C1为正方形,
∴OC1=C1B1=EC1=2,
∴B1(2,2),A1(2,0),
同理可得:C2是A1B1的中点,
∴B2(2+1=3,1),A2(3,0),
B3(2+1+ = , ),A3( ,0),
B4( + = , ),A4( ,0),
B5( + = , ).
故答案为:( ,0),( , ).
【分析】先根据直线y=﹣x+4计算与两坐标轴的交点可得:OE=OF=4,因为△EOF是等腰直角三角形,所以得△B1C1E是等腰直角三角形,再由正方形的边长相等得:C1是OE的中点,同理得:C2是A1B1的中点,C3是A2B2的中点,…,所以可得所求各点的坐标
15.【答案】解:①AC⊥BD
②四边形ABCD是菱形
证明:
∵四边形ABCD为平行四边形,
∴BO=DO,
∵AC⊥BD,
∴AC垂直平分BD,
∴AB=AD,
∴四边形ABCD为菱形
【解析】【分析】由命题的题设和结论可填出答案,由平行四边形的性质可证得AC为线段BD的垂直平分线,可求得AB=AD,可得四边形ABCD是菱形.
16.【答案】证明:∵点E、F是四边形ABCD的边AB、BC的中点,
∴EF= AC,EF∥AC,
∵点G、H是四边形ABCD的边CD、DA的中点,
∴GH= AC,GH∥AC,
∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形.
【解析】【分析】根据三角形的中位线定理,可得EF= AC,EF∥AC,GH= AC,GH∥AC,从而可得EF=GH,EF∥GH, 利用一组对边平行且相等的四边形是平行四边形即证.
17.【答案】(1)解:∵正方形的面积为 ,
∴正方形的边长为5cm.
(2)解:大的正方形的面积;
边长,边长不是整数,
,
.
【解析】【分析】(1)根据正方形的面积公式计算求解即可;
(2)根据正方形的面积公式求出 边长, 再根据 判断求解即可。
18.【答案】证明:四边形ABCD是菱形,
∴∠B=∠D,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF.
【解析】【分析】根据菱形的性质得到角和边相等,再利用“SAS”证明三角形全等,利用全等的性质求解即可。
19.【答案】(1)证明:∵BE⊥AC,CF⊥BD,
∴∠BEO=∠CFO=90°,
又∵BE=CF,∠BOE=∠COF
∴△BOE≌△COF;
∴OB=OC
∵平行四边形ABCD
∴OB=OC=OA=1/2AC
∴∠ABC=90°
∴平行四边形ABCD为矩形.
(2)解:在Rt△OCF中,OB=OC=OD=13
∴
∴BF=OB+OF=13+5=18.
【解析】【分析】(1)先利用AAS证明△BOE≌△COF,得出OB=OC,结合平行四边形的性质,得出OB=OC=OA,从而求出∠ABC=90°,即可得证;
(2)根据矩形的性质求出OC,然后利用勾股定理求OF即可.
20.【答案】(1)证明:∵CE平分 ,CF平分
∴ ,
∵
∴ ,
∴ ,
∴
∴
(2)当点O位于AC的中点时,四边形AECF是矩形
理由如下:
∵O是AC的中点
∴
由(1)得:
∴四边形AECF是平行四边形
∵ ,
∴
∴
即
∴四边形AECF是矩形.
【解析】【分析】(1)由于CE平分∠ACB,MN∥BC,故∠BCE=∠OEC=∠OCE,根据等角对等边得出OE=OC,同理可得OC=OF,故OC= ;
(2)根据平行四边形的判定定理可知,当OA=OC时,四边形AECF是矩形,由于CE、CF分别是∠ECO与∠OCF的平分线,故∠ECF是直角,则四边形AECF是矩形.
21.【答案】(1)证明:由旋转的性质得∠BCE=∠ACD,
∵AC=BC,
∴∠B=∠BAC,
∵CE=BE,
∴∠B=∠BCE,
∴∠ACD=∠BAC,
∴AB∥CD
(2)解:四边形BEDC是平行四边形,
由旋转的性质得CD=CE,
∵CE=BE,
∴CD=BE,
∵AB∥DC,
∴四边形BEDC是平行四边形.
【解析】【分析】(1)由旋转的性质得出∠BCE=∠ACD,由等腰三角形的性质得出∠B=∠BAC,∠B=∠BCE,由平行线的判定可得出结论;
(2)由平行四边形的判定可得出结论。
22.【答案】(1)证明:∵点O为对角线的中点,
∴,
∵,
∴,,
在和中,
,
∴;
(2)解:四边形为菱形,理由如下:
连接、,如图所示:
根据解析(1)可知,,
∴,
∵,
∴四边形为平行四边形,
∵,即,
∴四边形为菱形.
【解析】【分析】(1)先根据题意结合平行线的性质即可得到,,,再根据三角形全等的判定即可求解;
(2)四边形为菱形,连接、,先根据三角形全等的性质即可得到,再根据平行四边形的判定结合菱形的判定即可求解。
23.【答案】(1)证明:连接AC,∵∠1+∠2=60°,∠3+∠2=60°,∴∠1=∠3,∵∠BAD=120°,∴∠ABC=∠ADC=60°∵四边形ABCD是菱形,∴AB=BC=CD=AD,∴△ABC、△ACD为等边三角形∴∠4=60°,AC=AB,∴在△ABE和△ACF中, ,∴△ABE≌△ACF.(ASA)
∴BE=CF
(2)解:由(1)得△ABE≌△ACF,则S△ABE=S△ACF.
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,
是定值.
作AH⊥BC于H点,
则BH=2,S四边形AECF=S△ABC
=
= =
(3)解:由“垂线段最短”可知,
当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的面积会随着AE的变化而变化,且当AE最短时,
正三角形AEF的面积会最小,
又S△CEF=S四边形AECF﹣S△AEF,则△CEF的面积就会最大.
由(2)得,S△CEF=S四边形AECF﹣S△AEF
= ﹣ = .
【解析】【分析】(1)连接AC,由菱形的性质和已知条件用角边角易证△ABE≌△ACF,则BE=CF;
(2)作AH⊥BC于H点,根据全等三角形的面积相等可得S△ABE=S△ACF,则S四边形AECF=S△ABC,而三角形ABC的面积是定值,且三角形ABC的面积=BC AH,所以四边形AECF的面积即可求解;
(3)由“垂线段最短”可知,当正三角形AEF的边AE与BC垂直时,边AE最短,根据(2)中的结论即可求解。
1 / 1
一、单选题
1.下列哪个度数不可能是一个多边形的内角和( )
A. B. C. D.
2.平行四边形ABCD中,∠A=50°,则∠B的度数是( )
A.40° B.50° C.130° D.150°
3.如图,在中,,点为垂足,如果,则( )
A. B. C. D.
4.若菱形的两条对角线长分别为8和6,则这个菱形的面积是( )
A.96 B.48 C.24 D.12
5.下列命题为真命题的是( )
A.菱形的四个角相等 B.菱形的对角线相等
C.菱形的四条边互相垂直 D.菱形是轴对称图形
6.下列命题的逆命题正确的是( )
A.平行四边形的两组对边分别平行
B.对顶角相等
C.矩形是平行四边形
D.全等三角形的对应角相等
7.如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.
A.45 B.46 C.47 D.48
8.如图,在中,,,为斜边上一动点,,,垂足分别为、.则线段的最小值为
A. B. C. D.
9.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D同时出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,当四边形ABPQ初次为矩形时,点P和点Q运动的时间为( )秒.
A.2 B.3 C.4 D.5
10.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A.AC=BD B.BC=CD C.AD=BC D.AB=CD
二、填空题
11.如图,在△ABC中,D,E分别是AB,AC的中点.若BC=12,则DE的长为 .
12.一个多边形的每一个内角为108°,则这个多边形是 边形,它的内角和是
13.如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有 .(填序号)
14.如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBn n,则A3的坐标为 ,B5的坐标为 .
三、解答题
15.求证:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.
①已知:如图,在 ABCD中,对角线AC,BD交于点O, .
②求证:
16.如图,点E、F、G、H是四边形ABCD各边的中点,AC、BD是对角线.求证:四边形EFGH是平行四边形.
17.(1)在数学活动课上,老师要求同学利用手中纸片剪出一块面积为的正方形,试求出这个正方形的边长.
(2)小强的手中有两块边长都为的正方形纸片,他想将这两块正方形纸片沿对角线剪开,拼成如图所示的一个大正方形,请求出这个大正方形的面积.它的边长是整数吗 若不是整数,那么请你估计这个边长的值在哪两个整数之间.
18.如图,点E,F分别在菱形ABCD的边BC,CD上,且BE=DF.求证:∠BAE=∠DAF.
19.如图,在 ABCD中,对角线AC,BD相交于点O,BE⊥AC于点E,CF⊥BD于点F,BE CF.
(1)求证: ABCD是矩形.
(2)若OD=13,CF=12,求BF的长.
20.如图,在 中,点O是AC边的一个动点,过点O作 ,交 的平分线于点E,交 的外角平分线于点F,
(1)求证: ;
(2)当点O位于AC边的什么位置时四边形AECF是矩形?并说明理由.
21.如图,在△ABC中,AC=BC,E是AB上一点,且CE=BE,将△CBE绕点C旋转得到△CAD.
(1)求证:AB∥DC;
(2)连接DE,判断四边形BEDC的形状,并说明理由.
22.如图,四边形中,,点O为对角线的中点,过点O的直线l分别与、所在的直线相交于点E、F.(点E不与点D重合)
(1)求证:;
(2)当直线时,连接、,试判断四边形的形状,并说明理由.
23.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
答案解析部分
1.【答案】B
【解析】【解答】解:n边形的内角和为(n-2)×180°,故内角和为180°的倍数.
∵360°=2×180°,900°=5×180°,1800°=10×180°,
∴600°不可能是一个多边形的内角和.
故答案为:B.
【分析】n边形的内角和为(n-2)×180°,故内角和为180°的倍数,据此判断.
2.【答案】C
【解析】【解答】∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A=50°,
∴∠B=130°,
故答案为:C.
【分析】根据平行四边形的性质解决问题即可.
3.【答案】B
【解析】【解答】解:在 ABCD中,∠D=55°,
∴∠D=55°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠BCE=90°-∠B=35°.
故答案为:B.
【分析】由平行四边形的对角相等可得∠B,又由CE⊥AB,即可求得∠BCE的度数.
4.【答案】C
【解析】【解答】解:∵四边形ABCD是菱形,
∴S= ×6×8=24.
故答案为:C.
【分析】根据菱形的面积等于对角线乘积的一半计算即可.
5.【答案】D
【解析】【解答】解:A、菱形的四个角不一定相等,故错误,是假命题,不符合题意;
B、菱形的对角线互相垂直但不一定相等,故错误,是假命题,不符合题意;
C、菱形的四条边相等但不一定互相垂直,故错误,是假命题,不符合题意;
D、菱形是轴对称图形,正确,是真命题,符合题意.
故答案为:D.
【分析】A、矩形的四个角都相等,菱形的四个角不一定相等;
B、由菱形的性质可知:菱形的对角线互相垂直;
C、由菱形的性质可知:菱形的四条边相等;
D、由菱形的性质可知:菱形是轴对称图形.
6.【答案】A
【解析】【解答】解:A、逆命题:两组对边分别平行的四边形是平行四边形,逆命题正确,故符合题意;
B、逆命题:相等的角是对顶角,逆命题错误,故不符合题意;
C、逆命题:平行四边形是矩形,逆命题错误,故不符合题意;
D、逆命题:对应角相等的三角形全等,逆命题错误,故不符合题意;
故答案为:A.
【分析】分别写出各项中命题的逆命题,再判断真假即可.
7.【答案】D
【解析】【解答】解:作GM⊥EF于点M,如图所示:
由题意得:S⑤=S四边形ABCD﹣ (S①+S②+S③+S④)=4cm2,
∴S菱形EFGH=14+4=18cm2,
又∵∠F=30°,
设菱形的边长为x,则菱形的高为:GM=GF=vx,
根据菱形的面积公式得:x x=18,
解得:x=6,
∴菱形的边长为6cm,
而①②③④四个平行四边形周长的总和=2(AE+AH+HD+DG+GC+CF+FB+BE)=2(EF+FG+GH+HE)=48cm.
故选:D.
【分析】根据①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,可求出⑤的面积,从而可求出菱形的面积,根据菱形的性质可求出边长,进而可求出①②③④四个平行四边形周长的总和.
8.【答案】D
【解析】【解答】解:如图,连接CD,
,,,
四边形CEDF是矩形,
,
由垂线段最短可得CD⊥AB时线段EF的长最小,
,,
,
四边形CEDF是矩形,
.
故答案为:D.
【分析】连接CD,则四边形CEDF是矩形,EF=CD,由垂线段最短可得CD⊥AB时线段EF的长最小,利用勾股定理可得AB,然后根据等面积法可得CD,据此解答.
9.【答案】C
【解析】【解答】解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20-2x.
解得x=4,
故答案为:C.
【分析】设最快x秒,根据题意列出方程3x=20-2x,再求出x的值即可。
10.【答案】B
【解析】【分析】根据四边形ABCD中,∠A=∠B=∠C=90°,得出四边形ABCD是矩形,进而利用正方形的判定定理得出需要添加的条件.
【解答】∵四边形ABCD中,∠A=∠B=∠C=90°,
∴四边形ABCD是矩形,
当一组邻边相等时,矩形ABCD为正方形,
这个条件可以是:BC=DC.
故选B.
【点评】此题主要考查了正方形的判定,根据矩形的判定性质得出四边形ABCD是矩形是解决问题的关键.
11.【答案】6
【解析】【解答】解:∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
又BC=12,
∴
故答案为:6.
【分析】由题意可得DE是△ABC的中位线,则DE=BC,据此计算.
12.【答案】五;540°
【解析】【解答】解:∵多边形的每一个内角都等于108°,
∴多边形的每一个外角都等于180°﹣108°=72°,
∴边数n=360°÷72°=5,
内角和为(5﹣2)×180°=540°.
故答案为:五;540°.
【分析】先求出这个多边形的每一个外角的度数,再用360°除以一个外角的度数即可得到边数.
13.【答案】①②③④
【解析】【解答】解:证明:∵BC=EC,
∴∠CEB=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CEB=∠EBF,
∴∠CBE=∠EBF,
∴①BE平分∠CBF,正确;
∵BC=EC,CF⊥BE,
∴∠ECF=∠BCF,
∴②CF平分∠DCB,正确;
∵DC∥AB,
∴∠DCF=∠CFB,
∵∠ECF=∠BCF,
∴∠CFB=∠BCF,
∴BF=BC,
∴③正确;
∵FB=BC,CF⊥BE,
∴B点一定在FC的垂直平分线上,即PB垂直平分FC,
∴PF=PC,故④正确.
故答案为①②③④.
【分析】分别利用平行线的性质结合线段垂直平分线的性质以及等腰三角形的性质分别判断得出答案.
14.【答案】( ,0);( , )
【解析】【解答】解:当x=0,y=4,当y=0时,﹣x+4=0,x=4,
∴OE=OF=4,
∴△EOF是等腰直角三角形,
∴∠C1EF=45°
∴△B1C1E是等腰直角三角形,
∴B1C1=EC1,
∵四边形OA1B1C1为正方形,
∴OC1=C1B1=EC1=2,
∴B1(2,2),A1(2,0),
同理可得:C2是A1B1的中点,
∴B2(2+1=3,1),A2(3,0),
B3(2+1+ = , ),A3( ,0),
B4( + = , ),A4( ,0),
B5( + = , ).
故答案为:( ,0),( , ).
【分析】先根据直线y=﹣x+4计算与两坐标轴的交点可得:OE=OF=4,因为△EOF是等腰直角三角形,所以得△B1C1E是等腰直角三角形,再由正方形的边长相等得:C1是OE的中点,同理得:C2是A1B1的中点,C3是A2B2的中点,…,所以可得所求各点的坐标
15.【答案】解:①AC⊥BD
②四边形ABCD是菱形
证明:
∵四边形ABCD为平行四边形,
∴BO=DO,
∵AC⊥BD,
∴AC垂直平分BD,
∴AB=AD,
∴四边形ABCD为菱形
【解析】【分析】由命题的题设和结论可填出答案,由平行四边形的性质可证得AC为线段BD的垂直平分线,可求得AB=AD,可得四边形ABCD是菱形.
16.【答案】证明:∵点E、F是四边形ABCD的边AB、BC的中点,
∴EF= AC,EF∥AC,
∵点G、H是四边形ABCD的边CD、DA的中点,
∴GH= AC,GH∥AC,
∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形.
【解析】【分析】根据三角形的中位线定理,可得EF= AC,EF∥AC,GH= AC,GH∥AC,从而可得EF=GH,EF∥GH, 利用一组对边平行且相等的四边形是平行四边形即证.
17.【答案】(1)解:∵正方形的面积为 ,
∴正方形的边长为5cm.
(2)解:大的正方形的面积;
边长,边长不是整数,
,
.
【解析】【分析】(1)根据正方形的面积公式计算求解即可;
(2)根据正方形的面积公式求出 边长, 再根据 判断求解即可。
18.【答案】证明:四边形ABCD是菱形,
∴∠B=∠D,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF.
【解析】【分析】根据菱形的性质得到角和边相等,再利用“SAS”证明三角形全等,利用全等的性质求解即可。
19.【答案】(1)证明:∵BE⊥AC,CF⊥BD,
∴∠BEO=∠CFO=90°,
又∵BE=CF,∠BOE=∠COF
∴△BOE≌△COF;
∴OB=OC
∵平行四边形ABCD
∴OB=OC=OA=1/2AC
∴∠ABC=90°
∴平行四边形ABCD为矩形.
(2)解:在Rt△OCF中,OB=OC=OD=13
∴
∴BF=OB+OF=13+5=18.
【解析】【分析】(1)先利用AAS证明△BOE≌△COF,得出OB=OC,结合平行四边形的性质,得出OB=OC=OA,从而求出∠ABC=90°,即可得证;
(2)根据矩形的性质求出OC,然后利用勾股定理求OF即可.
20.【答案】(1)证明:∵CE平分 ,CF平分
∴ ,
∵
∴ ,
∴ ,
∴
∴
(2)当点O位于AC的中点时,四边形AECF是矩形
理由如下:
∵O是AC的中点
∴
由(1)得:
∴四边形AECF是平行四边形
∵ ,
∴
∴
即
∴四边形AECF是矩形.
【解析】【分析】(1)由于CE平分∠ACB,MN∥BC,故∠BCE=∠OEC=∠OCE,根据等角对等边得出OE=OC,同理可得OC=OF,故OC= ;
(2)根据平行四边形的判定定理可知,当OA=OC时,四边形AECF是矩形,由于CE、CF分别是∠ECO与∠OCF的平分线,故∠ECF是直角,则四边形AECF是矩形.
21.【答案】(1)证明:由旋转的性质得∠BCE=∠ACD,
∵AC=BC,
∴∠B=∠BAC,
∵CE=BE,
∴∠B=∠BCE,
∴∠ACD=∠BAC,
∴AB∥CD
(2)解:四边形BEDC是平行四边形,
由旋转的性质得CD=CE,
∵CE=BE,
∴CD=BE,
∵AB∥DC,
∴四边形BEDC是平行四边形.
【解析】【分析】(1)由旋转的性质得出∠BCE=∠ACD,由等腰三角形的性质得出∠B=∠BAC,∠B=∠BCE,由平行线的判定可得出结论;
(2)由平行四边形的判定可得出结论。
22.【答案】(1)证明:∵点O为对角线的中点,
∴,
∵,
∴,,
在和中,
,
∴;
(2)解:四边形为菱形,理由如下:
连接、,如图所示:
根据解析(1)可知,,
∴,
∵,
∴四边形为平行四边形,
∵,即,
∴四边形为菱形.
【解析】【分析】(1)先根据题意结合平行线的性质即可得到,,,再根据三角形全等的判定即可求解;
(2)四边形为菱形,连接、,先根据三角形全等的性质即可得到,再根据平行四边形的判定结合菱形的判定即可求解。
23.【答案】(1)证明:连接AC,∵∠1+∠2=60°,∠3+∠2=60°,∴∠1=∠3,∵∠BAD=120°,∴∠ABC=∠ADC=60°∵四边形ABCD是菱形,∴AB=BC=CD=AD,∴△ABC、△ACD为等边三角形∴∠4=60°,AC=AB,∴在△ABE和△ACF中, ,∴△ABE≌△ACF.(ASA)
∴BE=CF
(2)解:由(1)得△ABE≌△ACF,则S△ABE=S△ACF.
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,
是定值.
作AH⊥BC于H点,
则BH=2,S四边形AECF=S△ABC
=
= =
(3)解:由“垂线段最短”可知,
当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的面积会随着AE的变化而变化,且当AE最短时,
正三角形AEF的面积会最小,
又S△CEF=S四边形AECF﹣S△AEF,则△CEF的面积就会最大.
由(2)得,S△CEF=S四边形AECF﹣S△AEF
= ﹣ = .
【解析】【分析】(1)连接AC,由菱形的性质和已知条件用角边角易证△ABE≌△ACF,则BE=CF;
(2)作AH⊥BC于H点,根据全等三角形的面积相等可得S△ABE=S△ACF,则S四边形AECF=S△ABC,而三角形ABC的面积是定值,且三角形ABC的面积=BC AH,所以四边形AECF的面积即可求解;
(3)由“垂线段最短”可知,当正三角形AEF的边AE与BC垂直时,边AE最短,根据(2)中的结论即可求解。
1 / 1
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
