冀教版八年级数学下册第二十一章一次函数单元复习题(含解析)
文档属性
| 名称 | 冀教版八年级数学下册第二十一章一次函数单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 373.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 15:09:27 | ||
图片预览




文档简介
冀教版八年级数学下册第二十一章一次函数单元复习题
一、单选题
1.函数y=3x+1的图象一定经过点( )
A.(3,5) B.(﹣2,3) C.(2,7) D.(4,10)
2.某水池现有水100m3,每小时进水20m3,排水15m3,t小时后水池中的水为Qm3,它的解析式为( )
A.Q=100+20t B.Q=100-15t C.Q=100+5t D.Q=100-5t
3.下列函数中是一次函数的为( )
A.y=8x2 B.y=x+1 C.y= D.y=
4.定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”,例如:M(1,1),N(﹣2,﹣2)都是“平衡点”,当﹣1≤x≤3时,直线y=2x+m上有“平衡点”,则m的取值范围是( )
A.0≤m≤1 B.﹣1≤m≤0 C.﹣3≤m≤3 D.﹣3≤m≤1
5.若点(4,y1),(-2,y2)都在函数y=-3x+m的图象上,则y1与y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.无法确定
6.一次函数 的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.若,则一次函数的图象是( )
A. B.
C. D.
8.一次函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
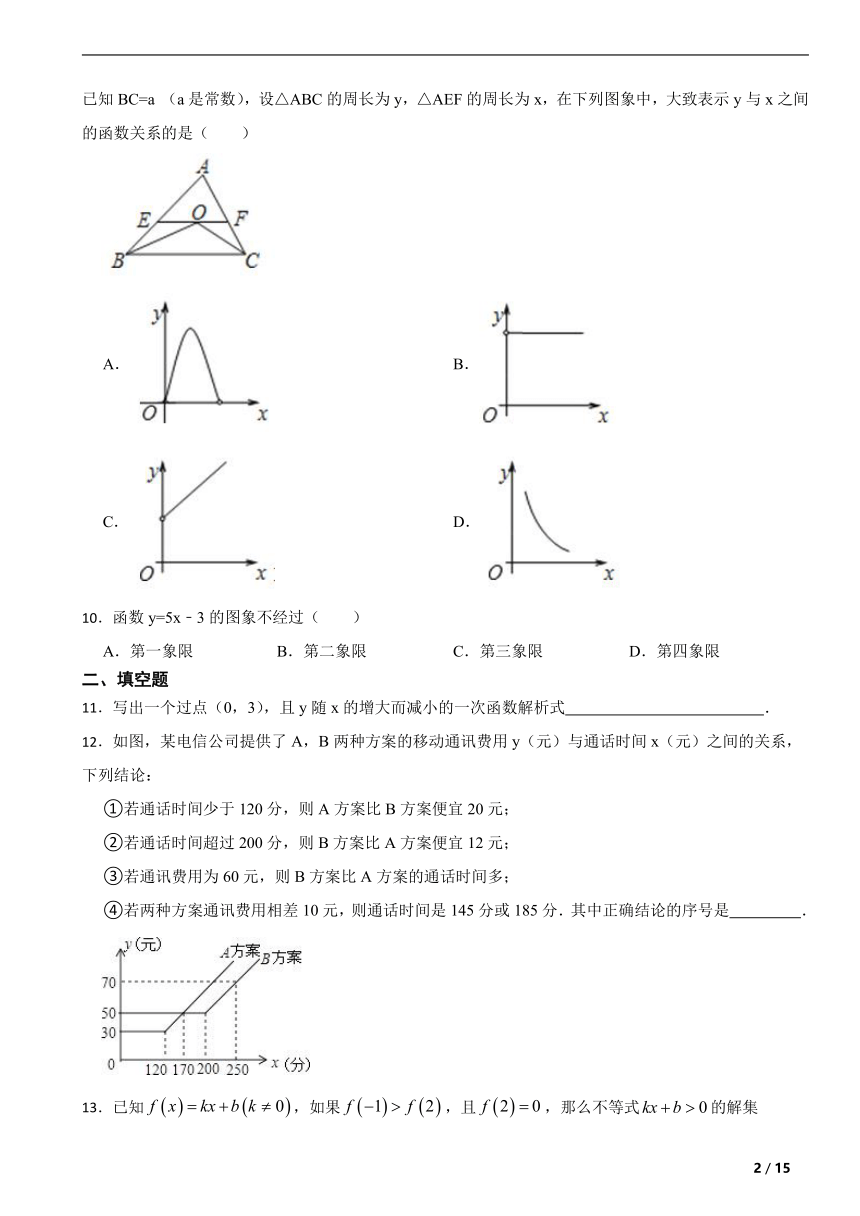
9.在△ABC中,点O是△ABC的内心,连接OB、OC,过点O作EF∥BC分别交AB、AC于点E、F,已知BC=a (a是常数),设△ABC的周长为y,△AEF的周长为x,在下列图象中,大致表示y与x之间的函数关系的是( )
A. B.
C. D.
10.函数y=5x﹣3的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题
11.写出一个过点(0,3),且y随x的增大而减小的一次函数解析式 .
12.如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:
①若通话时间少于120分,则A方案比B方案便宜20元;
②若通话时间超过200分,则B方案比A方案便宜12元;
③若通讯费用为60元,则B方案比A方案的通话时间多;
④若两种方案通讯费用相差10元,则通话时间是145分或185分.其中正确结论的序号是 .
13.已知,如果,且,那么不等式的解集是 .
14.小明爸爸开车带小明去青岛游玩,一路上匀速前行,小明记下了如下数据
观察时刻 9:00 9:06 9:18 (注:“青岛90km”表 示离青岛的距离为90km)
路牌内容 青岛90km 青岛80km 青岛60km
从9点开始,记汽车行驶的时间为t(min),汽车离青岛的距离为s(km),则s关于t的表达式为, .
三、解答题
15.《算法统宗》中记载了一个“李白沾酒”的故事,诗云:“今携一壶酒,游春郊外走。逢朋加一倍入店饮半斗.相逢三处店,饮尽壶中酒.试问能算士,如何知原有.”(注:古代一斗是10升)译文:李白在郊外春游时,做出这样一条约定;遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒,按照这样的约定,在第3个店里遇到朋友时,李白正好喝光了壶中的酒,请问各位,壶中原有多少升酒?
16.利用一次函数的图象解二元一次方程组: .
17.请你用学习“一次函数”时积累的经验和方法解决下列问题:
(1)在平面直角坐标系中,画出函数y=|x|的图象:
①列表填空:
x … ﹣3 ﹣2 ﹣1 0 1 2 3 …
y …
…
②描点、连线,画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|两条不同类型的性质;
(3)写出函数y=|x|与y=|x+2|图象的平移关系.
18.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是什么?
19.小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离 y (千米)和所用的时间 x (小时)之间的函数关系如图所示.
(1)小王从乙地返回甲地用了多少小时?
(2)求小李出发6小时后距离甲地多远?
(3)在甲、乙两地之间有一丙地,小李从去时途经丙地,到返回时路过丙地,共用了2小时50分钟,求甲、丙两地相距多远?
20.每年“双11"天猫商城都会推出各种优惠活动进行促销,今年,王阿姨的“双11“到来之前准备在两家天期店铺中选择一家购买原价均为10000元/条的被子2条和原价均为600元/个的颈椎枕若干个,已如网家店铺在活动明间分别给子以下优惠:
A店铺:"双11"当天购实所有商品可以享受8折优惠:
B店铺:买2条被子,赠送1个预椎枕、同时“双11"当天下单,还可立减160元;
设购买颈椎枕x(个),若王阿姨在“双11"当天下单,A,B两个店铺优惠后所付金额分别为yA(元)、yB(元)。
(1)试分别表示yA、yB与x的函数关系式;
(2)王阿姨准备在”双11"当天购买4个颈椎枕,通过计算说明在哪家店铺购买更省钱?
21.下表是某奶茶店的一款奶茶近两天的销售情况.
销售情况 销售数量(单位:杯) 销售收入 (单位:元)
小杯 大杯
第一天 20 30 460
第二天 25 25 450
(1)问这款奶茶小杯和大杯的销售单价各是多少元?
(2)已知这款奶茶小杯成本4元杯,大杯成本5元杯,奶茶店每天只能供应80杯该款奶茶,其中小杯不少于10杯,求该款奶茶一天的最大利润.(销售利润销售收入成本)
(3)为了满足市场的需求,奶茶店推出每杯2元的加料服务,顾客在选完杯型后可以自主选择加料或者不加料.小明恰好用了208元购买该款奶茶,其中小杯不加料的数量是总杯数的,则小明这款奶茶大杯加料的买了 杯.
22.习总书记在2020年9月30日的联合国生物多样性峰会上提出“中国在2030年前实现碳达峰,2060年前实现碳中和”的目标,加速了新能源汽车取代燃油汽车的步伐.某新能源汽车经销商购进 、 两种型号的新能源汽车,其中 型车的进货单价比 型汽车的进货单价多2万元;花50万元购进 型汽车的数量与花40万元购进 型汽车的数量相同.
(1)求 、 两种型号汽车的进货单价:
(2)由于新能源汽车需求不断增加,该店准备购进 , 两种型号的新能源汽车60辆,已知 型车的售价为12.5万元/辆, 型车的售价为10万元/辆.根据销售经验,购进 型车的数量不少于 型车的2倍,设购进 辆 型车,60辆车全部售完获利 万元,该经销商应购进 , 两种型号车各多少辆,才能使 最大? 最大为多少万元?
23.如图,一次函数的图象与y轴交于点B,与正比例函数的图象相交于点,且.
(1)分别求出这两个函数的解析式;
(2)求的面积;
(3)点P在x轴上,且是等腰三角形,请直接写出点P的坐标.
答案解析部分
1.【答案】C
【解析】【解答】A、把x=3代入y=3x+1,解得y=10,所以图象不经过点(3,5),A不符合题意;
B、把x=﹣2代入y=3x+1,解得y=﹣5,所以图象不经过点(﹣2,3),B不符合题意;
C、把x=2代入y=3x+1,解得y=7,所以图象经过点(2,7),C符合题意;
D、把x=4代入y=3x+1,解得y=13,所以图象不经过点(4,10),D不符合题意.
故答案为:C.
【分析】将各点的坐标代入函数解析式进行检验即可.
2.【答案】C
【解析】【解答】Q=100+20t-15t=100+5t
故答案为:C.
【分析】由题意可得t小时后水池中的余水量Q=水池中原有的水量+t小时的进水量-t小时的排水量即可求解。
3.【答案】B
【解析】【解答】解:A、自变量次数不为1,故不为一次函数;
B、是一次函数;
C、为反比例函数;
D、分母中含有未知数不是一次函数.
所以B选项是正确的.
【分析】根据一次函数的定义逐一分析即可.
4.【答案】D
【解析】【解答】解:∵x=y,
∴x=2x+m,即x=﹣m.
∵﹣1≤x≤3,
∴﹣1≤﹣m≤3,
∴﹣3≤m≤1.
故D符合题意.
故答案为:D.
【分析】解答此题的关键是理解新定义(平衡点).根据平衡点的定义得到x=-m,再代入﹣1≤x≤3可求得m的范围.
5.【答案】B
【解析】【解答】解:当x=4时,y1=-3×4+m=-12+m,
当x=-2时,y2=-3×(-2)+m=6+m,
∴y1故答案为:B.
【分析】利用一次函数的性质求解即可。
6.【答案】B
【解析】【解答】解:∵ ,
∴函数图象一定经过一、三象限;
又∵ ,函数与y轴交于y轴负半轴,
∴函数经过一、三、四象限,不经过第二象限
故答案为:B
【分析】由二次函数 ,可得函数图象经过一、三、四象限,所以不经过第二象限
7.【答案】A
【解析】【解答】解:∵,
∴k-1>0,1-k<0,
∴y的值随x的增大而增大,且与y轴的负半轴相交.
故答案为:A.
【分析】根据可得k-1>0,1-k<0,再利用一次函数的图象与系数的关系可得答案。
8.【答案】C
【解析】【解答】解:∵ <0,6>0,
∴图象经过一、二、四象限,不经过第三象限.
故答案为:C.
【分析】y=ax+b(a≠0),当a>0,b>0时,图象过一、二、三象;当a>0,b<0时,图象过一、三、四象限;当a<0,b>0时,图象过一、二、四象限;当a<0,b<0时,图象过二、三、四象限,据此即可判断得出答案.
9.【答案】C
【解析】【解答】解:如图,
∵点O是△ABC的内心,
∴∠1=∠2,
又∵EF∥BC,
∴∠3=∠2,
∴∠1=∠3,
∴EO=EB,
同理可得FO=FC,
∵x=AE+EO+FO+AF,
y=AE+BE+AF+FC+BC,
∴y=x+a,(x>0),
即y是x的一次函数,
所以C选项正确.
故选C.
【分析】由于点O是△ABC的内心,根据内心的性质得到OB、OC分别平分∠ABC、∠ACB,又EF∥BC,可得到∠1=∠3,则EO=EB,同理可得FO=FC,再根据周长的所以可得到y=x+a,(x>0),即它是一次函数,即可得到正确选项.
10.【答案】B
【解析】【解答】解:因为解析式y=5x﹣3中,k=5>0,图象过一、三象限,b=﹣3<0,图象过一、三、四象限,故图象不经过第二象限.
故答案为:B.
【分析】y=ax+b(a≠0),当a>0,b>0时,图象过一、二、三象;当a>0,b<0时,图象过一、三、四象限;当a<0,b>0时,图象过一、二、四象限;当a<0,b<0时,图象过二、三、四象限.
11.【答案】y=-x+3(答案不唯一)
【解析】【解答】解:设函数y=kx+b (k≠0,k,b为常数),
∵图象经过点(0,3) .
∴b=3,
又∵y随x的增大而减小,
∴k<0,可取k= 1.
这样满足条件的函数可以为: y= x+3.
故答案为:y= x+3.
【分析】设函数y=kx+b (k≠0,k,b为常数),将(0,3)代入求出b值,由y随x的增大而减小,可得k<0,据此即得结论(答案不唯一).
12.【答案】①②③
【解析】【解答】解:依题意得
A:(1)当0≤x≤120,yA=30,
⑵当x>120,yA=30+(x﹣120)×[(50﹣30)÷(170﹣120)]=0.4x﹣18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70﹣50)÷(250﹣200)](x﹣200)=0.4x﹣30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x﹣18,∴x=195,
B:60=0.4x﹣30,∴x=225,故(3)正确;
将yA=40或60代入,得x=145分或195分,故(4)错误;
故答案为:①②③.
【分析】根据图象知道:在通话170分钟收费一样,在通话120时A收费30元,B收费50元,其中A超过120分钟后每分钟加收0.4元,B超过200分钟加收每分钟0.4元,由此即可确定正确结论.
13.【答案】
【解析】【解答】解:∵,,
∴y随x的增大而减小,
∵,
∴不等式的解集是x<2,
故答案为:x<2.
【分析】根据题意先求出y随x的增大而减小,再根据判断求解即可。
14.【答案】
【解析】【解答】解:由表知,汽车每6min行驶10km,
∴汽车的速度为 (km/min),
则 ,
故答案为: .
【分析】由路程、时间和速度的关系得出汽车的行驶速度,根据汽车离青岛的距离=90 行驶的路程可得函数解析式.
15.【答案】解:假设壶中原来有x升酒。
2[2(2x-5)-5]-5=0
4x-15=
4x=
x=
x=4.375
【解析】【分析】可以设壶中原来有x升酒,根据题意列出方程,解方程得到答案即可。
16.【答案】解:如图,
两个一次函数y=﹣ x+ 与y=3x﹣2的交点坐标为(1,1);
因此方程组 的解 .
【解析】【分析】先把两个方程化成一次函数的形式,然后在同一坐标系中画出它们的图象,交点的坐标就是方程组的解.
17.【答案】解:(1)①填表正确;
x … ﹣3 ﹣2 ﹣1 0 1 2 3 …
y … 3 2 1 0 1 2 3 …
②画函数图象如图:
(2)①增减性:x<0时,y随x的增大而减小
x>0时,y随x的增大而增大
②对称性:图象关于y轴对称
③函数的最小值为0;
(3)把y=|x|向左平移两个单位得到y=|x+2|
或把y=|x+2|向右平移两个单位得到y=|x|.
【解析】【分析】(1)列表画出图象解答即可;
(2)根据一次函数的性质解答即可;
(3)根据平移的特点解答即可.
18.【答案】解:设过点(1,1)和(0,﹣1)的直线解析式为y=kx+b,
则 ,解得 ,
所以过点(1,1)和(0,﹣1)的直线解析式为y=2x﹣1;
设过点(1,1)和(0,2)的直线解析式为y=mx+n,
则,即得,
所以过点(1,1)和(0,2)的直线解析式为y=﹣x+2,
所以所解的二元一次方程组为.
【解析】【分析】先利用待定系数求出两函数解析式,由于函数图象交点坐标为两函数解析式组成的方程组的解,则可判断所解的二元一次方程组为两解析式所组成的方程组.
19.【答案】(1)解:7.5-3.5=4(小时)
答:小王从乙地返回甲地用了4小时
(2)解:设小李返回时直线解析式为 将(3.5,240)、(7.5,0)代入得:
解得:
∴∴当 时,
答:小李出发6小时后距离甲地90千米
(3)解:设小李前往乙地的直线解析式为 将(3,240)代入得: 解得: ∴ 解得:
当 时,
答:甲、丙两地相距160千米
【解析】【分析】(1)用总时间减去去的时间和中间休息的时间得出答案;
(2)首先设返回时的函数解析式为y=kx+b,然后将(3.5,240)和(7.5,0)代入函数解析式求出解析式,然后将x=6代入函数解析式求出答案;
(3)设小李前往乙地的直线解析式为y=kx,将(3,240)得出函数解析式,然后联立两个函数解析式求出x的值,然后将x的值代入解析式求出答案.
20.【答案】(1)解:由题意得:
yA=1000×2×0.8+0.8×600x=480x+1600;
yB= 1000×2+600(x-1)-160=600x+1240
(2)解:当x=4时,ya=480×4+1600=3520;
yB= 600×4+1240=3640;
∵3520<3640,
∴在A店铺购买更省钱
【解析】【分析】(1)根据题意,列出关系式即可;
(2)将x=4代入关系式,通过比较大小即可得到答案。
21.【答案】(1)解:设小杯奶茶销售单价为元,大杯奶茶销售单价为元,
根据题意,得,
解得,
答:小杯奶茶销售单价为8元,大杯奶茶销售单价为10元
(2)解:设售出小杯奶茶杯,总利润为元,
则,
,,
随的增大而减小,
当时,的最小值为390元
(3)6
【解析】【解答】解:(3)设小杯不加料奶茶为p杯,其中小杯加料和大杯不加料共q杯,则大杯加料奶茶为杯,
根据题意,得:,
整理,得:,
解得,
,
即小明这款奶茶大杯加料的买了6杯.
故答案为:6.
【分析】(1)设小杯奶茶销售单价为a元,大杯奶茶销售单价为b元, 根据单价×数量=收入结合表格中的数据可得20a+30b=460、25a+25b=450,联立求解即可;
(2)设售出小杯奶茶m杯,总利润为w元,根据数量×成本=利润可得w与m的关系式,然后利用一次函数的性质进行解答;
(3)设小杯不加料奶茶为p杯,其中小杯加料和大杯不加料共q杯,则大杯加料奶茶为(2p-q)杯,根据费用为208元可得关于p、q的方程,结合p、q为正整数可得p、q的值,据此求解.
22.【答案】(1)解:设 型汽车的进货单价为 万元,则 型汽车的进货单价为 万元,
,
解得 ,
经检验, 是原方程的解,且符合实际.
∴ 、 两种型号的汽车的进货单价分别是10万元和8万元.
答: 、 两种型号的汽车的进货单价分别是10万元和8万元.
(2)解: ,
∵ ,
∴ ,
∵ ,
∴ 随 的增大而增大,
∴当 时, .
∴该店应购进 型汽车20辆、 型汽车40辆时,利润最大,最大利润是130万元.
答:该店应购进 型汽车20辆、 型汽车40辆时,利润最大,最大利润是130万元.
【解析】【分析】(1)设 型汽车的进货单价为 万元,则 型汽车的进货单价为 万元,根据“花50万元购进 型汽车的数量与花40万元购进 型汽车的数量相同”列出方程,解方程即可;
(2)根据题意列出w与a的一次函数解析式,再确定a的取值范围,根据一次函数的性质即可求解。
23.【答案】(1)解:∵正比例函数的图象经过点,
∴,
∴,
∴正比例函数解析式为.
如图1中,过A作轴于C,
在中,,
,
∴,
∴,
∴,解得,
∴一次函数的解析式为.
(2)解:如图1中,过A作轴于D,
∵,
∴,
∴,
(3)点的坐标或或或
【解析】【解答】解:(3)当时,,,
当时,,
当时,线段的垂直平分线为,
∴,
满足条件的点P的坐标或或或.
【分析】(1)将点A(3,4)代入中,可求出k1的值, 过A作轴于C, 由勾股定理可得AO=5,即得OB=5,从而得出B(0,-5),再利用待定系数法求出一次函数解析式即可;
(2)过A作轴于D,根据即可求解;
(3)分三种情况:,和时,据此分别求解即可.
1 / 1
一、单选题
1.函数y=3x+1的图象一定经过点( )
A.(3,5) B.(﹣2,3) C.(2,7) D.(4,10)
2.某水池现有水100m3,每小时进水20m3,排水15m3,t小时后水池中的水为Qm3,它的解析式为( )
A.Q=100+20t B.Q=100-15t C.Q=100+5t D.Q=100-5t
3.下列函数中是一次函数的为( )
A.y=8x2 B.y=x+1 C.y= D.y=
4.定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”,例如:M(1,1),N(﹣2,﹣2)都是“平衡点”,当﹣1≤x≤3时,直线y=2x+m上有“平衡点”,则m的取值范围是( )
A.0≤m≤1 B.﹣1≤m≤0 C.﹣3≤m≤3 D.﹣3≤m≤1
5.若点(4,y1),(-2,y2)都在函数y=-3x+m的图象上,则y1与y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.无法确定
6.一次函数 的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.若,则一次函数的图象是( )
A. B.
C. D.
8.一次函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.在△ABC中,点O是△ABC的内心,连接OB、OC,过点O作EF∥BC分别交AB、AC于点E、F,已知BC=a (a是常数),设△ABC的周长为y,△AEF的周长为x,在下列图象中,大致表示y与x之间的函数关系的是( )
A. B.
C. D.
10.函数y=5x﹣3的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题
11.写出一个过点(0,3),且y随x的增大而减小的一次函数解析式 .
12.如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:
①若通话时间少于120分,则A方案比B方案便宜20元;
②若通话时间超过200分,则B方案比A方案便宜12元;
③若通讯费用为60元,则B方案比A方案的通话时间多;
④若两种方案通讯费用相差10元,则通话时间是145分或185分.其中正确结论的序号是 .
13.已知,如果,且,那么不等式的解集是 .
14.小明爸爸开车带小明去青岛游玩,一路上匀速前行,小明记下了如下数据
观察时刻 9:00 9:06 9:18 (注:“青岛90km”表 示离青岛的距离为90km)
路牌内容 青岛90km 青岛80km 青岛60km
从9点开始,记汽车行驶的时间为t(min),汽车离青岛的距离为s(km),则s关于t的表达式为, .
三、解答题
15.《算法统宗》中记载了一个“李白沾酒”的故事,诗云:“今携一壶酒,游春郊外走。逢朋加一倍入店饮半斗.相逢三处店,饮尽壶中酒.试问能算士,如何知原有.”(注:古代一斗是10升)译文:李白在郊外春游时,做出这样一条约定;遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒,按照这样的约定,在第3个店里遇到朋友时,李白正好喝光了壶中的酒,请问各位,壶中原有多少升酒?
16.利用一次函数的图象解二元一次方程组: .
17.请你用学习“一次函数”时积累的经验和方法解决下列问题:
(1)在平面直角坐标系中,画出函数y=|x|的图象:
①列表填空:
x … ﹣3 ﹣2 ﹣1 0 1 2 3 …
y …
…
②描点、连线,画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|两条不同类型的性质;
(3)写出函数y=|x|与y=|x+2|图象的平移关系.
18.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是什么?
19.小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离 y (千米)和所用的时间 x (小时)之间的函数关系如图所示.
(1)小王从乙地返回甲地用了多少小时?
(2)求小李出发6小时后距离甲地多远?
(3)在甲、乙两地之间有一丙地,小李从去时途经丙地,到返回时路过丙地,共用了2小时50分钟,求甲、丙两地相距多远?
20.每年“双11"天猫商城都会推出各种优惠活动进行促销,今年,王阿姨的“双11“到来之前准备在两家天期店铺中选择一家购买原价均为10000元/条的被子2条和原价均为600元/个的颈椎枕若干个,已如网家店铺在活动明间分别给子以下优惠:
A店铺:"双11"当天购实所有商品可以享受8折优惠:
B店铺:买2条被子,赠送1个预椎枕、同时“双11"当天下单,还可立减160元;
设购买颈椎枕x(个),若王阿姨在“双11"当天下单,A,B两个店铺优惠后所付金额分别为yA(元)、yB(元)。
(1)试分别表示yA、yB与x的函数关系式;
(2)王阿姨准备在”双11"当天购买4个颈椎枕,通过计算说明在哪家店铺购买更省钱?
21.下表是某奶茶店的一款奶茶近两天的销售情况.
销售情况 销售数量(单位:杯) 销售收入 (单位:元)
小杯 大杯
第一天 20 30 460
第二天 25 25 450
(1)问这款奶茶小杯和大杯的销售单价各是多少元?
(2)已知这款奶茶小杯成本4元杯,大杯成本5元杯,奶茶店每天只能供应80杯该款奶茶,其中小杯不少于10杯,求该款奶茶一天的最大利润.(销售利润销售收入成本)
(3)为了满足市场的需求,奶茶店推出每杯2元的加料服务,顾客在选完杯型后可以自主选择加料或者不加料.小明恰好用了208元购买该款奶茶,其中小杯不加料的数量是总杯数的,则小明这款奶茶大杯加料的买了 杯.
22.习总书记在2020年9月30日的联合国生物多样性峰会上提出“中国在2030年前实现碳达峰,2060年前实现碳中和”的目标,加速了新能源汽车取代燃油汽车的步伐.某新能源汽车经销商购进 、 两种型号的新能源汽车,其中 型车的进货单价比 型汽车的进货单价多2万元;花50万元购进 型汽车的数量与花40万元购进 型汽车的数量相同.
(1)求 、 两种型号汽车的进货单价:
(2)由于新能源汽车需求不断增加,该店准备购进 , 两种型号的新能源汽车60辆,已知 型车的售价为12.5万元/辆, 型车的售价为10万元/辆.根据销售经验,购进 型车的数量不少于 型车的2倍,设购进 辆 型车,60辆车全部售完获利 万元,该经销商应购进 , 两种型号车各多少辆,才能使 最大? 最大为多少万元?
23.如图,一次函数的图象与y轴交于点B,与正比例函数的图象相交于点,且.
(1)分别求出这两个函数的解析式;
(2)求的面积;
(3)点P在x轴上,且是等腰三角形,请直接写出点P的坐标.
答案解析部分
1.【答案】C
【解析】【解答】A、把x=3代入y=3x+1,解得y=10,所以图象不经过点(3,5),A不符合题意;
B、把x=﹣2代入y=3x+1,解得y=﹣5,所以图象不经过点(﹣2,3),B不符合题意;
C、把x=2代入y=3x+1,解得y=7,所以图象经过点(2,7),C符合题意;
D、把x=4代入y=3x+1,解得y=13,所以图象不经过点(4,10),D不符合题意.
故答案为:C.
【分析】将各点的坐标代入函数解析式进行检验即可.
2.【答案】C
【解析】【解答】Q=100+20t-15t=100+5t
故答案为:C.
【分析】由题意可得t小时后水池中的余水量Q=水池中原有的水量+t小时的进水量-t小时的排水量即可求解。
3.【答案】B
【解析】【解答】解:A、自变量次数不为1,故不为一次函数;
B、是一次函数;
C、为反比例函数;
D、分母中含有未知数不是一次函数.
所以B选项是正确的.
【分析】根据一次函数的定义逐一分析即可.
4.【答案】D
【解析】【解答】解:∵x=y,
∴x=2x+m,即x=﹣m.
∵﹣1≤x≤3,
∴﹣1≤﹣m≤3,
∴﹣3≤m≤1.
故D符合题意.
故答案为:D.
【分析】解答此题的关键是理解新定义(平衡点).根据平衡点的定义得到x=-m,再代入﹣1≤x≤3可求得m的范围.
5.【答案】B
【解析】【解答】解:当x=4时,y1=-3×4+m=-12+m,
当x=-2时,y2=-3×(-2)+m=6+m,
∴y1
【分析】利用一次函数的性质求解即可。
6.【答案】B
【解析】【解答】解:∵ ,
∴函数图象一定经过一、三象限;
又∵ ,函数与y轴交于y轴负半轴,
∴函数经过一、三、四象限,不经过第二象限
故答案为:B
【分析】由二次函数 ,可得函数图象经过一、三、四象限,所以不经过第二象限
7.【答案】A
【解析】【解答】解:∵,
∴k-1>0,1-k<0,
∴y的值随x的增大而增大,且与y轴的负半轴相交.
故答案为:A.
【分析】根据可得k-1>0,1-k<0,再利用一次函数的图象与系数的关系可得答案。
8.【答案】C
【解析】【解答】解:∵ <0,6>0,
∴图象经过一、二、四象限,不经过第三象限.
故答案为:C.
【分析】y=ax+b(a≠0),当a>0,b>0时,图象过一、二、三象;当a>0,b<0时,图象过一、三、四象限;当a<0,b>0时,图象过一、二、四象限;当a<0,b<0时,图象过二、三、四象限,据此即可判断得出答案.
9.【答案】C
【解析】【解答】解:如图,
∵点O是△ABC的内心,
∴∠1=∠2,
又∵EF∥BC,
∴∠3=∠2,
∴∠1=∠3,
∴EO=EB,
同理可得FO=FC,
∵x=AE+EO+FO+AF,
y=AE+BE+AF+FC+BC,
∴y=x+a,(x>0),
即y是x的一次函数,
所以C选项正确.
故选C.
【分析】由于点O是△ABC的内心,根据内心的性质得到OB、OC分别平分∠ABC、∠ACB,又EF∥BC,可得到∠1=∠3,则EO=EB,同理可得FO=FC,再根据周长的所以可得到y=x+a,(x>0),即它是一次函数,即可得到正确选项.
10.【答案】B
【解析】【解答】解:因为解析式y=5x﹣3中,k=5>0,图象过一、三象限,b=﹣3<0,图象过一、三、四象限,故图象不经过第二象限.
故答案为:B.
【分析】y=ax+b(a≠0),当a>0,b>0时,图象过一、二、三象;当a>0,b<0时,图象过一、三、四象限;当a<0,b>0时,图象过一、二、四象限;当a<0,b<0时,图象过二、三、四象限.
11.【答案】y=-x+3(答案不唯一)
【解析】【解答】解:设函数y=kx+b (k≠0,k,b为常数),
∵图象经过点(0,3) .
∴b=3,
又∵y随x的增大而减小,
∴k<0,可取k= 1.
这样满足条件的函数可以为: y= x+3.
故答案为:y= x+3.
【分析】设函数y=kx+b (k≠0,k,b为常数),将(0,3)代入求出b值,由y随x的增大而减小,可得k<0,据此即得结论(答案不唯一).
12.【答案】①②③
【解析】【解答】解:依题意得
A:(1)当0≤x≤120,yA=30,
⑵当x>120,yA=30+(x﹣120)×[(50﹣30)÷(170﹣120)]=0.4x﹣18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70﹣50)÷(250﹣200)](x﹣200)=0.4x﹣30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x﹣18,∴x=195,
B:60=0.4x﹣30,∴x=225,故(3)正确;
将yA=40或60代入,得x=145分或195分,故(4)错误;
故答案为:①②③.
【分析】根据图象知道:在通话170分钟收费一样,在通话120时A收费30元,B收费50元,其中A超过120分钟后每分钟加收0.4元,B超过200分钟加收每分钟0.4元,由此即可确定正确结论.
13.【答案】
【解析】【解答】解:∵,,
∴y随x的增大而减小,
∵,
∴不等式的解集是x<2,
故答案为:x<2.
【分析】根据题意先求出y随x的增大而减小,再根据判断求解即可。
14.【答案】
【解析】【解答】解:由表知,汽车每6min行驶10km,
∴汽车的速度为 (km/min),
则 ,
故答案为: .
【分析】由路程、时间和速度的关系得出汽车的行驶速度,根据汽车离青岛的距离=90 行驶的路程可得函数解析式.
15.【答案】解:假设壶中原来有x升酒。
2[2(2x-5)-5]-5=0
4x-15=
4x=
x=
x=4.375
【解析】【分析】可以设壶中原来有x升酒,根据题意列出方程,解方程得到答案即可。
16.【答案】解:如图,
两个一次函数y=﹣ x+ 与y=3x﹣2的交点坐标为(1,1);
因此方程组 的解 .
【解析】【分析】先把两个方程化成一次函数的形式,然后在同一坐标系中画出它们的图象,交点的坐标就是方程组的解.
17.【答案】解:(1)①填表正确;
x … ﹣3 ﹣2 ﹣1 0 1 2 3 …
y … 3 2 1 0 1 2 3 …
②画函数图象如图:
(2)①增减性:x<0时,y随x的增大而减小
x>0时,y随x的增大而增大
②对称性:图象关于y轴对称
③函数的最小值为0;
(3)把y=|x|向左平移两个单位得到y=|x+2|
或把y=|x+2|向右平移两个单位得到y=|x|.
【解析】【分析】(1)列表画出图象解答即可;
(2)根据一次函数的性质解答即可;
(3)根据平移的特点解答即可.
18.【答案】解:设过点(1,1)和(0,﹣1)的直线解析式为y=kx+b,
则 ,解得 ,
所以过点(1,1)和(0,﹣1)的直线解析式为y=2x﹣1;
设过点(1,1)和(0,2)的直线解析式为y=mx+n,
则,即得,
所以过点(1,1)和(0,2)的直线解析式为y=﹣x+2,
所以所解的二元一次方程组为.
【解析】【分析】先利用待定系数求出两函数解析式,由于函数图象交点坐标为两函数解析式组成的方程组的解,则可判断所解的二元一次方程组为两解析式所组成的方程组.
19.【答案】(1)解:7.5-3.5=4(小时)
答:小王从乙地返回甲地用了4小时
(2)解:设小李返回时直线解析式为 将(3.5,240)、(7.5,0)代入得:
解得:
∴∴当 时,
答:小李出发6小时后距离甲地90千米
(3)解:设小李前往乙地的直线解析式为 将(3,240)代入得: 解得: ∴ 解得:
当 时,
答:甲、丙两地相距160千米
【解析】【分析】(1)用总时间减去去的时间和中间休息的时间得出答案;
(2)首先设返回时的函数解析式为y=kx+b,然后将(3.5,240)和(7.5,0)代入函数解析式求出解析式,然后将x=6代入函数解析式求出答案;
(3)设小李前往乙地的直线解析式为y=kx,将(3,240)得出函数解析式,然后联立两个函数解析式求出x的值,然后将x的值代入解析式求出答案.
20.【答案】(1)解:由题意得:
yA=1000×2×0.8+0.8×600x=480x+1600;
yB= 1000×2+600(x-1)-160=600x+1240
(2)解:当x=4时,ya=480×4+1600=3520;
yB= 600×4+1240=3640;
∵3520<3640,
∴在A店铺购买更省钱
【解析】【分析】(1)根据题意,列出关系式即可;
(2)将x=4代入关系式,通过比较大小即可得到答案。
21.【答案】(1)解:设小杯奶茶销售单价为元,大杯奶茶销售单价为元,
根据题意,得,
解得,
答:小杯奶茶销售单价为8元,大杯奶茶销售单价为10元
(2)解:设售出小杯奶茶杯,总利润为元,
则,
,,
随的增大而减小,
当时,的最小值为390元
(3)6
【解析】【解答】解:(3)设小杯不加料奶茶为p杯,其中小杯加料和大杯不加料共q杯,则大杯加料奶茶为杯,
根据题意,得:,
整理,得:,
解得,
,
即小明这款奶茶大杯加料的买了6杯.
故答案为:6.
【分析】(1)设小杯奶茶销售单价为a元,大杯奶茶销售单价为b元, 根据单价×数量=收入结合表格中的数据可得20a+30b=460、25a+25b=450,联立求解即可;
(2)设售出小杯奶茶m杯,总利润为w元,根据数量×成本=利润可得w与m的关系式,然后利用一次函数的性质进行解答;
(3)设小杯不加料奶茶为p杯,其中小杯加料和大杯不加料共q杯,则大杯加料奶茶为(2p-q)杯,根据费用为208元可得关于p、q的方程,结合p、q为正整数可得p、q的值,据此求解.
22.【答案】(1)解:设 型汽车的进货单价为 万元,则 型汽车的进货单价为 万元,
,
解得 ,
经检验, 是原方程的解,且符合实际.
∴ 、 两种型号的汽车的进货单价分别是10万元和8万元.
答: 、 两种型号的汽车的进货单价分别是10万元和8万元.
(2)解: ,
∵ ,
∴ ,
∵ ,
∴ 随 的增大而增大,
∴当 时, .
∴该店应购进 型汽车20辆、 型汽车40辆时,利润最大,最大利润是130万元.
答:该店应购进 型汽车20辆、 型汽车40辆时,利润最大,最大利润是130万元.
【解析】【分析】(1)设 型汽车的进货单价为 万元,则 型汽车的进货单价为 万元,根据“花50万元购进 型汽车的数量与花40万元购进 型汽车的数量相同”列出方程,解方程即可;
(2)根据题意列出w与a的一次函数解析式,再确定a的取值范围,根据一次函数的性质即可求解。
23.【答案】(1)解:∵正比例函数的图象经过点,
∴,
∴,
∴正比例函数解析式为.
如图1中,过A作轴于C,
在中,,
,
∴,
∴,
∴,解得,
∴一次函数的解析式为.
(2)解:如图1中,过A作轴于D,
∵,
∴,
∴,
(3)点的坐标或或或
【解析】【解答】解:(3)当时,,,
当时,,
当时,线段的垂直平分线为,
∴,
满足条件的点P的坐标或或或.
【分析】(1)将点A(3,4)代入中,可求出k1的值, 过A作轴于C, 由勾股定理可得AO=5,即得OB=5,从而得出B(0,-5),再利用待定系数法求出一次函数解析式即可;
(2)过A作轴于D,根据即可求解;
(3)分三种情况:,和时,据此分别求解即可.
1 / 1
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
