2023年山东省枣庄市薛城区舜耕中学九年级中考模拟数学模拟预测题(含答案)
文档属性
| 名称 | 2023年山东省枣庄市薛城区舜耕中学九年级中考模拟数学模拟预测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 15:08:28 | ||
图片预览



文档简介
2023年九年级学业水平模拟考试数学试卷
一、选择题:本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是正确的.
1.下列各数是负数的是( )
A. B. C. D.
2.如图是由几个大小相同的小正方体搭成的几何体,若去掉1号小正方体,则下列说法正确的是( )
A.左视图和俯视图不变 B.主视图和左视图不变
C.主视图和俯视图不变 D.都不变
3.第五套人民币硬币分为兰花1角、荷花5角、菊花1元.自古以来人们就把兰花视为高洁、典雅、爱国和坚贞不渝的象征.硬币兰花1角的直径约是19毫米,则数据“19毫米"用科学记数法表示为( )
A.米 B.米
C.米 D.米
4.第24届北京冬季奥林匹克会于2022年2月4日至2月20日成功举行.下列四个图分别是四届冬奥会图标中的一部分,其中是轴对称图形的为( )
A. B. C. D.
5.下列运算结果正确的是( )
A. B.
C. D.
6.小泽同学在折幸运星时将一张长方形的纸条折成了如图所示的样子(内部有一个正五边形),则的度数为( )
A.36° B.54° C.60° D.72°
7.在平面直角坐标系中,将点向上平移3个单位长度,再向左平移2个单位长度,得到点,则点的坐标是( )
A. B. C. D.
8.如图,菱形ABCD的对角线AC与BD相交于点O,E为AD的中点,连接OE,,,则( )
A.4 B. C.2 D.
9.如图,在正方形ABCD中,AE平分交BC于点E,点F是边AB上一点,连接DF,若,则的度数为( )
A.45° B.60° C.67.5° D.77.5°
10.如图是二次函数图象的一部分,图象过点,对称轴为直线,①;②;③当时,;④若,为函数图象上的两点,则,以上结论中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本大题共6小题,满分18分,只填写最后结果,每小题填对得3分.
11.分解因式:________.
12.若实数m,n满足,则________.
13.已知关于x的分式方程的解为非负数,则m的取值范围是________.
14.如图,将矩形ABCD绕点B逆时针旋转30°得到矩形,点C的对应点恰好落在边AD上,若,则的长为________.
第14题图
15.在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“ 优选法 ”,在全国大规模推广,取得了很大成果.如图所示,利用黄金分割法,所作EF将矩形窗框ABCD分为上下两部分,其中E为边AB的黄金分割点,即.已知AB为2米,则线段BE的长为________米.
第15题图
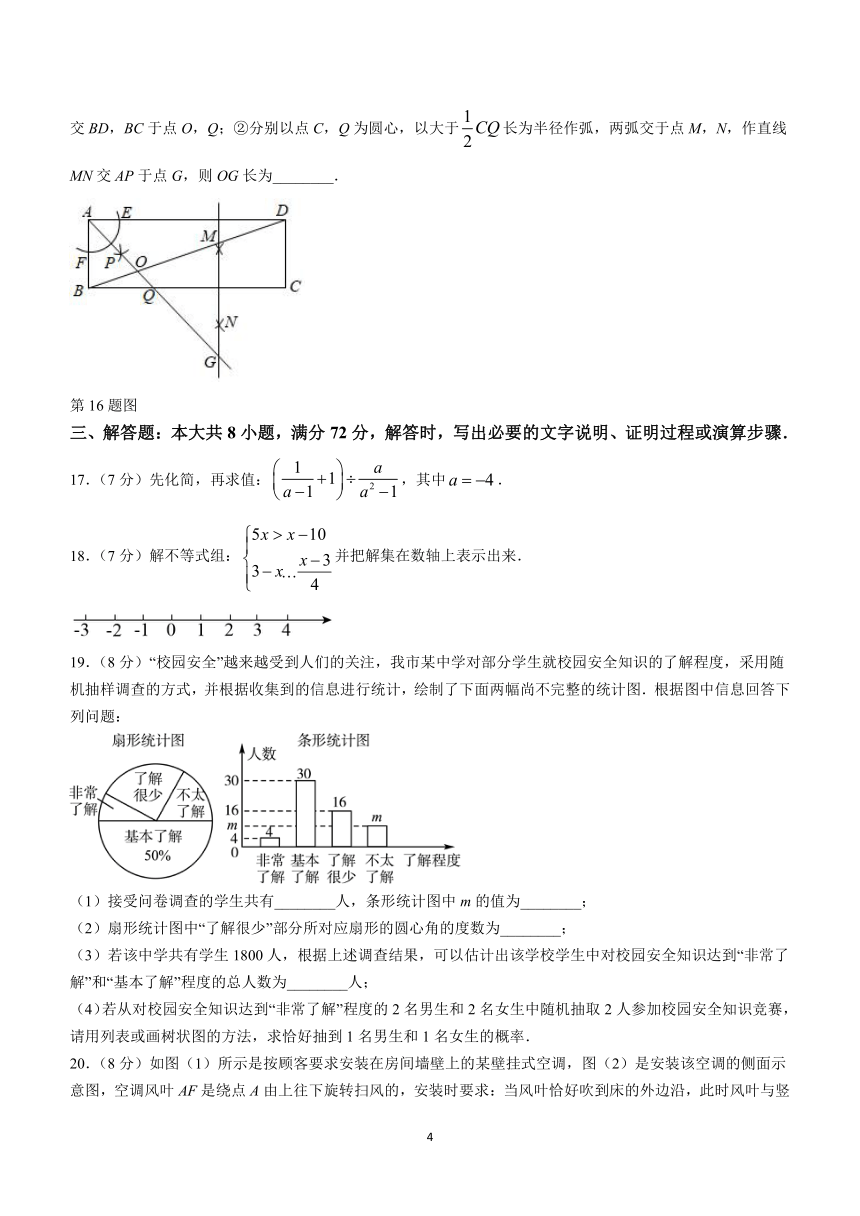
16.如图,在矩形ABCD中,,.①以点A为圆心,以不大于AB长为半径作弧,分别交边AD,AB于点E,F,再分别以点E,F为圆心,以大于长为半径作弧,两弧交于点P,作射线AP分别交BD,BC于点O,Q;②分别以点C,Q为圆心,以大于长为半径作弧,两弧交于点M,N,作直线MN交AP于点G,则OG长为________.
第16题图
三、解答题:本大共8小题,满分72分,解答时,写出必要的文字说明、证明过程或演算步骤.
17.(7分)先化简,再求值:,其中.
18.(7分)解不等式组:并把解集在数轴上表示出来.
19.(8分)“校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
(1)接受问卷调查的学生共有________人,条形统计图中m的值为________;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为________;
(3)若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为________人;
(4)若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
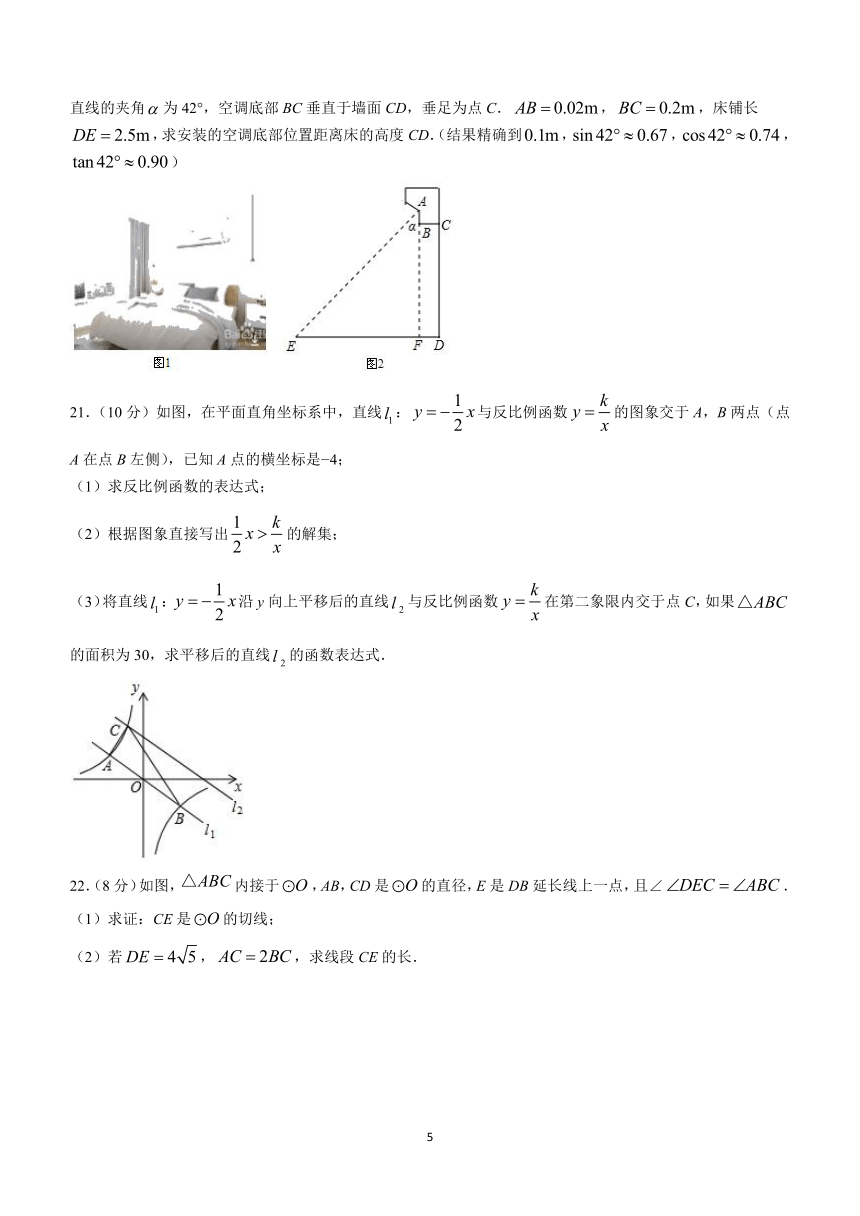
20.(8分)如图(1)所示是按顾客要求安装在房间墙壁上的某壁挂式空调,图(2)是安装该空调的侧面示意图,空调风叶AF是绕点A由上往下旋转扫风的,安装时要求:当风叶恰好吹到床的外边沿,此时风叶与竖直线的夹角为42°,空调底部BC垂直于墙面CD,垂足为点C.,,床铺长,求安装的空调底部位置距离床的高度CD.(结果精确到,,,)
21.(10分)如图,在平面直角坐标系中,直线:与反比例函数的图象交于A,B两点(点A在点B左侧),已知A点的横坐标是 4;
(1)求反比例函数的表达式;
(2)根据图象直接写出的解集;
(3)将直线:沿y向上平移后的直线与反比例函数在第二象限内交于点C,如果的面积为30,求平移后的直线的函数表达式.
22.(8分)如图,内接于,AB,CD是的直径,E是DB延长线上一点,且∠.
(1)求证:CE是的切线;
(2)若,,求线段CE的长.
23.(12分)【感知】小亮遇到了这样一道题:已知如图①在中,,D在AB上,E在AC的延长上,DE交BC于点F,且,求证:.
小亮仔细分析了题中的已知条件后,如图②过D点作交BC于G,进而解决了该问题.(不需要证明)
【探究】如图③,在四边形ABCD中,,E为BC边的中点,,AF与DC的延长线交于点F,试探究线段AB与AF、CF之间的数量关系,并证明你的结论.
【应用】如图④,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若,,,则GF的长为________.
24(12分).如图,在平面直角坐标系中,二次函数交轴于点、,交y轴于点,在y轴上有一点,连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴上方的一个动点,求面积的最大值;
(3)抛物线对称轴上是否存在点P,使为等腰三角形,若存在,请直接写出所有P点的坐标,若不存在请说明理由.
2023年九年级学业水平模拟考试数学试卷
参考答案
评卷说明:
1.选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分.
2.解答题每小题的解答中所对应的分数,是指考生正确解答到该步所应得的累计分数,本答案中每小题只给出一种解法, 考生的其他解法,请参照评分意见进行评分.
3.如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确角解答分数的一半,若出现较严重的逻错误,后续部分不给分
一、选择题(本大题共10小题,每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B B B D A C C C
二、填空题:(本大题共6小题,每小题3分,共18分)
11. 12.7 13.且 14. 15. 16.
三、解答题:(本大题共8小题,共72分)
17.解:
,………………5分
当时,原式.………………7分
18.解:解不等式,得:,………………2分
解不等式,得:,………………4分
所以不等式组的解集是,………………5分
将解集表示在数轴上如下:
………………7分
19.
解:(1)接受问卷调查的学生共有(人),;
故答案为:60,10;………………2分
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数;
故答案为:96°;………………4分
(3)该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为:(人);
故答案为:1020;………………6分
(4)由题意列树状图:
由树状图可知,所有等可能的结果有12种,恰好抽到1名男生和1名女生的结果有8种,
∴恰好抽到1名男生和1名女生的概率为.………………8分
20.解:,,
,………………2分
在中,,
,………………5分
………………7分
∴安装的空调底部位置距离床的高度CD为.………………8分
21.解:(1)∵直线:经过点A,A点的纵坐标是2,
∴当时,,
∴,
∵反比例函数的图象经过点A,
,
∴反比例函数的表达式为;………………2分
(2)∵直线:与反比例函数的图象交于A,B两点,
∴,………………4分
∴不等式的解集为或;………………6分
(3)如图,设平移后的直线与x轴交于点D,连接AD,BD,
,
的面积与的面积相等,
的面积为30,
,即,
,
,
,………………8分
设平移后的直线的函数表达式为,
把代入,可得,
解得,
∴平移后的直线的函数表达式为.………………10分.
22(1)证明:是的直径,
,
,
,
,………………1分
又,
,
,
,
是的半径,
是的切线;………………3分
(2)解:由(1)知,,
在和中,
,,
,
即,
,………………5分
在中,,,
,
解得,
即线段CE的长为4.………………8分
23.【探究】解:.………………1分
如图1,分别延长DC、AE,交于G点,
,
,,
∵E为BC边的中点,
,
,
,………………3分
又,
,
而,
,
,………………5分
.………………6分
【应用】解:如图2,延长GE交CB的延长线于M.
∵四边形ABCD是正方形,
,
,
在和中,
,
,………………8分
,,
,
,………………10分
,
,………………11分,
.………………12分
24.解:(1)∵二次函数经过点,,,
,
解得,
所以二次函数的解析式为:,………………3分
(2)由,,可求AE所在直线解析式为,
过点D作轴于G,交AE于点F,交x轴于点G,过点E作,垂足为H,如图
设,则点,
,………………5分
,
∴当时,的面积取得最大值为.………………7分
(3)的对称轴为,,
设,又,,
可求,,,
当时,,
解得,,此时;………………8分
当时,,
解得,,此时点P坐标为;………………9分
当时,,
解得,,此时点P坐标为:.………………11分
综上所述,
P点的坐标为:,,.………………12分
一、选择题:本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是正确的.
1.下列各数是负数的是( )
A. B. C. D.
2.如图是由几个大小相同的小正方体搭成的几何体,若去掉1号小正方体,则下列说法正确的是( )
A.左视图和俯视图不变 B.主视图和左视图不变
C.主视图和俯视图不变 D.都不变
3.第五套人民币硬币分为兰花1角、荷花5角、菊花1元.自古以来人们就把兰花视为高洁、典雅、爱国和坚贞不渝的象征.硬币兰花1角的直径约是19毫米,则数据“19毫米"用科学记数法表示为( )
A.米 B.米
C.米 D.米
4.第24届北京冬季奥林匹克会于2022年2月4日至2月20日成功举行.下列四个图分别是四届冬奥会图标中的一部分,其中是轴对称图形的为( )
A. B. C. D.
5.下列运算结果正确的是( )
A. B.
C. D.
6.小泽同学在折幸运星时将一张长方形的纸条折成了如图所示的样子(内部有一个正五边形),则的度数为( )
A.36° B.54° C.60° D.72°
7.在平面直角坐标系中,将点向上平移3个单位长度,再向左平移2个单位长度,得到点,则点的坐标是( )
A. B. C. D.
8.如图,菱形ABCD的对角线AC与BD相交于点O,E为AD的中点,连接OE,,,则( )
A.4 B. C.2 D.
9.如图,在正方形ABCD中,AE平分交BC于点E,点F是边AB上一点,连接DF,若,则的度数为( )
A.45° B.60° C.67.5° D.77.5°
10.如图是二次函数图象的一部分,图象过点,对称轴为直线,①;②;③当时,;④若,为函数图象上的两点,则,以上结论中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本大题共6小题,满分18分,只填写最后结果,每小题填对得3分.
11.分解因式:________.
12.若实数m,n满足,则________.
13.已知关于x的分式方程的解为非负数,则m的取值范围是________.
14.如图,将矩形ABCD绕点B逆时针旋转30°得到矩形,点C的对应点恰好落在边AD上,若,则的长为________.
第14题图
15.在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“ 优选法 ”,在全国大规模推广,取得了很大成果.如图所示,利用黄金分割法,所作EF将矩形窗框ABCD分为上下两部分,其中E为边AB的黄金分割点,即.已知AB为2米,则线段BE的长为________米.
第15题图
16.如图,在矩形ABCD中,,.①以点A为圆心,以不大于AB长为半径作弧,分别交边AD,AB于点E,F,再分别以点E,F为圆心,以大于长为半径作弧,两弧交于点P,作射线AP分别交BD,BC于点O,Q;②分别以点C,Q为圆心,以大于长为半径作弧,两弧交于点M,N,作直线MN交AP于点G,则OG长为________.
第16题图
三、解答题:本大共8小题,满分72分,解答时,写出必要的文字说明、证明过程或演算步骤.
17.(7分)先化简,再求值:,其中.
18.(7分)解不等式组:并把解集在数轴上表示出来.
19.(8分)“校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
(1)接受问卷调查的学生共有________人,条形统计图中m的值为________;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为________;
(3)若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为________人;
(4)若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
20.(8分)如图(1)所示是按顾客要求安装在房间墙壁上的某壁挂式空调,图(2)是安装该空调的侧面示意图,空调风叶AF是绕点A由上往下旋转扫风的,安装时要求:当风叶恰好吹到床的外边沿,此时风叶与竖直线的夹角为42°,空调底部BC垂直于墙面CD,垂足为点C.,,床铺长,求安装的空调底部位置距离床的高度CD.(结果精确到,,,)
21.(10分)如图,在平面直角坐标系中,直线:与反比例函数的图象交于A,B两点(点A在点B左侧),已知A点的横坐标是 4;
(1)求反比例函数的表达式;
(2)根据图象直接写出的解集;
(3)将直线:沿y向上平移后的直线与反比例函数在第二象限内交于点C,如果的面积为30,求平移后的直线的函数表达式.
22.(8分)如图,内接于,AB,CD是的直径,E是DB延长线上一点,且∠.
(1)求证:CE是的切线;
(2)若,,求线段CE的长.
23.(12分)【感知】小亮遇到了这样一道题:已知如图①在中,,D在AB上,E在AC的延长上,DE交BC于点F,且,求证:.
小亮仔细分析了题中的已知条件后,如图②过D点作交BC于G,进而解决了该问题.(不需要证明)
【探究】如图③,在四边形ABCD中,,E为BC边的中点,,AF与DC的延长线交于点F,试探究线段AB与AF、CF之间的数量关系,并证明你的结论.
【应用】如图④,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若,,,则GF的长为________.
24(12分).如图,在平面直角坐标系中,二次函数交轴于点、,交y轴于点,在y轴上有一点,连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴上方的一个动点,求面积的最大值;
(3)抛物线对称轴上是否存在点P,使为等腰三角形,若存在,请直接写出所有P点的坐标,若不存在请说明理由.
2023年九年级学业水平模拟考试数学试卷
参考答案
评卷说明:
1.选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分.
2.解答题每小题的解答中所对应的分数,是指考生正确解答到该步所应得的累计分数,本答案中每小题只给出一种解法, 考生的其他解法,请参照评分意见进行评分.
3.如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确角解答分数的一半,若出现较严重的逻错误,后续部分不给分
一、选择题(本大题共10小题,每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B B B D A C C C
二、填空题:(本大题共6小题,每小题3分,共18分)
11. 12.7 13.且 14. 15. 16.
三、解答题:(本大题共8小题,共72分)
17.解:
,………………5分
当时,原式.………………7分
18.解:解不等式,得:,………………2分
解不等式,得:,………………4分
所以不等式组的解集是,………………5分
将解集表示在数轴上如下:
………………7分
19.
解:(1)接受问卷调查的学生共有(人),;
故答案为:60,10;………………2分
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数;
故答案为:96°;………………4分
(3)该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为:(人);
故答案为:1020;………………6分
(4)由题意列树状图:
由树状图可知,所有等可能的结果有12种,恰好抽到1名男生和1名女生的结果有8种,
∴恰好抽到1名男生和1名女生的概率为.………………8分
20.解:,,
,………………2分
在中,,
,………………5分
………………7分
∴安装的空调底部位置距离床的高度CD为.………………8分
21.解:(1)∵直线:经过点A,A点的纵坐标是2,
∴当时,,
∴,
∵反比例函数的图象经过点A,
,
∴反比例函数的表达式为;………………2分
(2)∵直线:与反比例函数的图象交于A,B两点,
∴,………………4分
∴不等式的解集为或;………………6分
(3)如图,设平移后的直线与x轴交于点D,连接AD,BD,
,
的面积与的面积相等,
的面积为30,
,即,
,
,
,………………8分
设平移后的直线的函数表达式为,
把代入,可得,
解得,
∴平移后的直线的函数表达式为.………………10分.
22(1)证明:是的直径,
,
,
,
,………………1分
又,
,
,
,
是的半径,
是的切线;………………3分
(2)解:由(1)知,,
在和中,
,,
,
即,
,………………5分
在中,,,
,
解得,
即线段CE的长为4.………………8分
23.【探究】解:.………………1分
如图1,分别延长DC、AE,交于G点,
,
,,
∵E为BC边的中点,
,
,
,………………3分
又,
,
而,
,
,………………5分
.………………6分
【应用】解:如图2,延长GE交CB的延长线于M.
∵四边形ABCD是正方形,
,
,
在和中,
,
,………………8分
,,
,
,………………10分
,
,………………11分,
.………………12分
24.解:(1)∵二次函数经过点,,,
,
解得,
所以二次函数的解析式为:,………………3分
(2)由,,可求AE所在直线解析式为,
过点D作轴于G,交AE于点F,交x轴于点G,过点E作,垂足为H,如图
设,则点,
,………………5分
,
∴当时,的面积取得最大值为.………………7分
(3)的对称轴为,,
设,又,,
可求,,,
当时,,
解得,,此时;………………8分
当时,,
解得,,此时点P坐标为;………………9分
当时,,
解得,,此时点P坐标为:.………………11分
综上所述,
P点的坐标为:,,.………………12分
同课章节目录
