【备课参考】2015秋华师大版九年级数学教学课件:23.2相似图形(共23张PPT)
文档属性
| 名称 | 【备课参考】2015秋华师大版九年级数学教学课件:23.2相似图形(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-29 15:02:07 | ||
图片预览





文档简介
课件23张PPT。23.2相似图形学习目标1.从生活中形状相同的图形的实例中认识图形的相似,理解相似图形的性质和概念.?
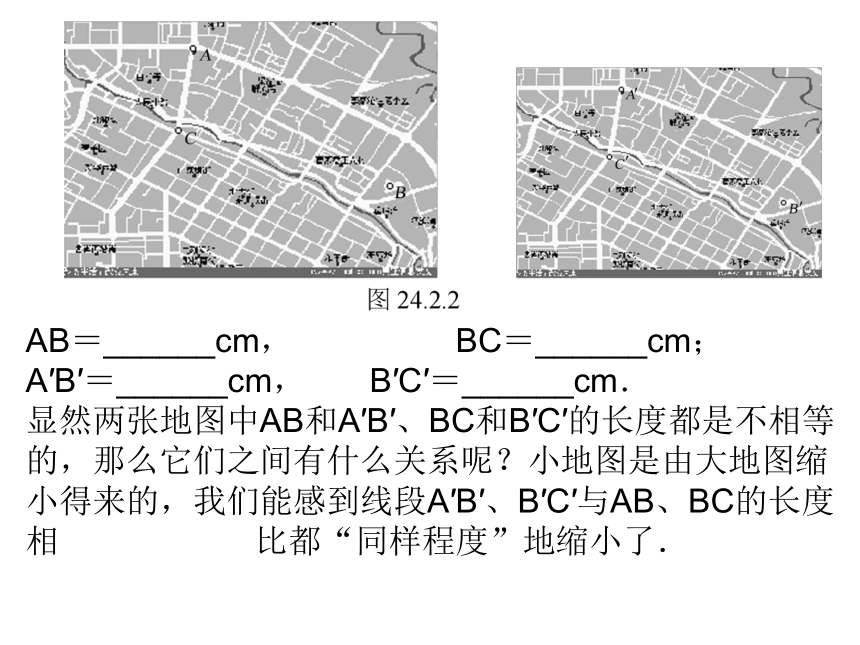
2.会利用相似图形的性质和概念进行计算和证明.? 两个相似的平面图形之间有什么关系呢?为什么有些图形是相似的,而有些不是呢?相似图形有什么主要性质呢?创设情境 明确目标合作探究 达成目标 图24.2.2是某个城市的大小不同的两张地图,当然,它们是相似的图形.设在大地图中有A、B、C三地,在小地图中的相应三地记为A′、B′、C′,试用刻度尺量一量两张地图中A(A′)与B(B′)两地之间的图上距离、B(B′)与C(C′)两地之间的图上距离.AB=______cm, BC=______cm;
A′B′=______cm, B′C′=______cm.
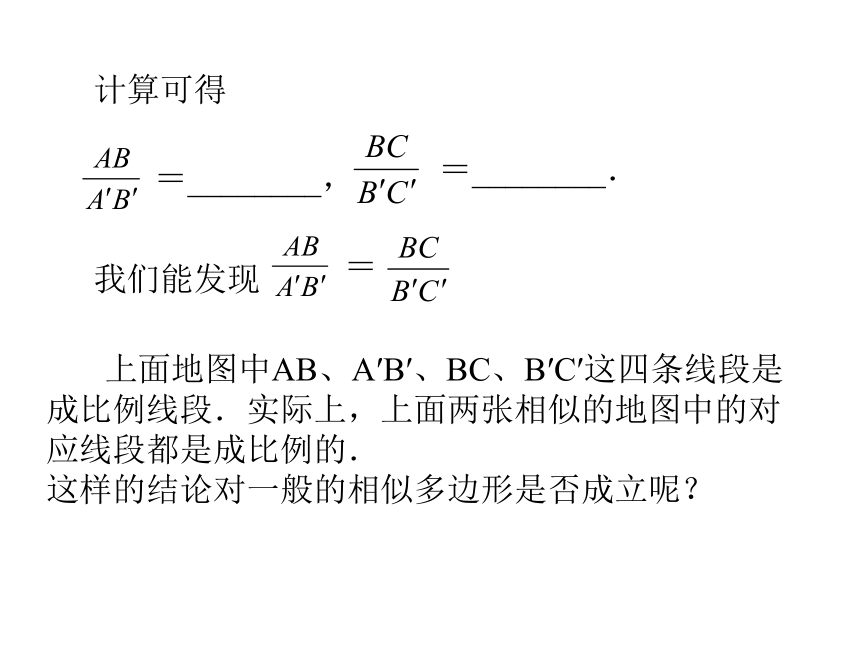
显然两张地图中AB和A′B′、BC和B′C′的长度都是不相等的,那么它们之间有什么关系呢?小地图是由大地图缩小得来的,我们能感到线段A′B′、B′C′与AB、BC的长度相 比都“同样程度”地缩小了. 计算可得=________,=________. 上面地图中AB、A′B′、BC、B′C′这四条线段是成比例线段.实际上,上面两张相似的地图中的对应线段都是成比例的.
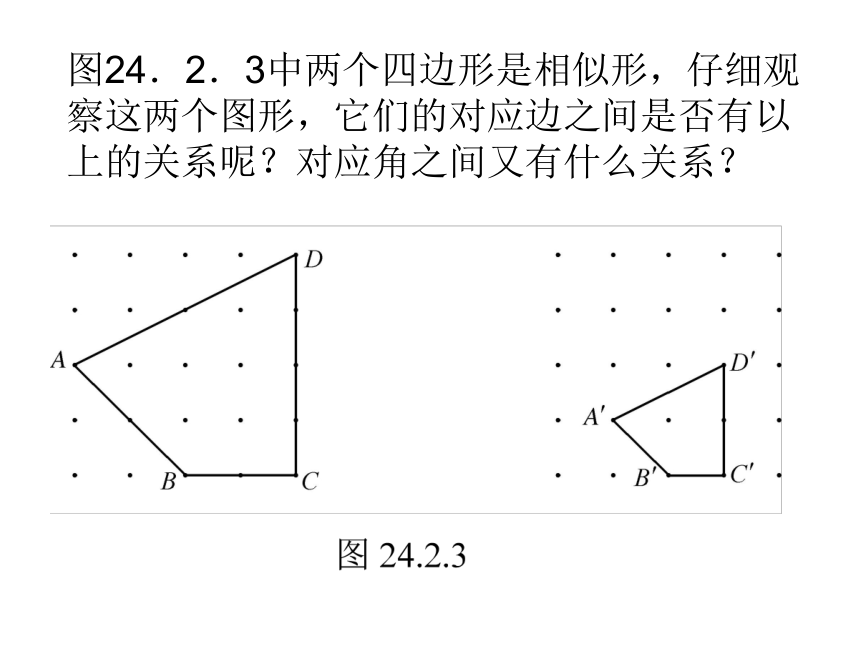
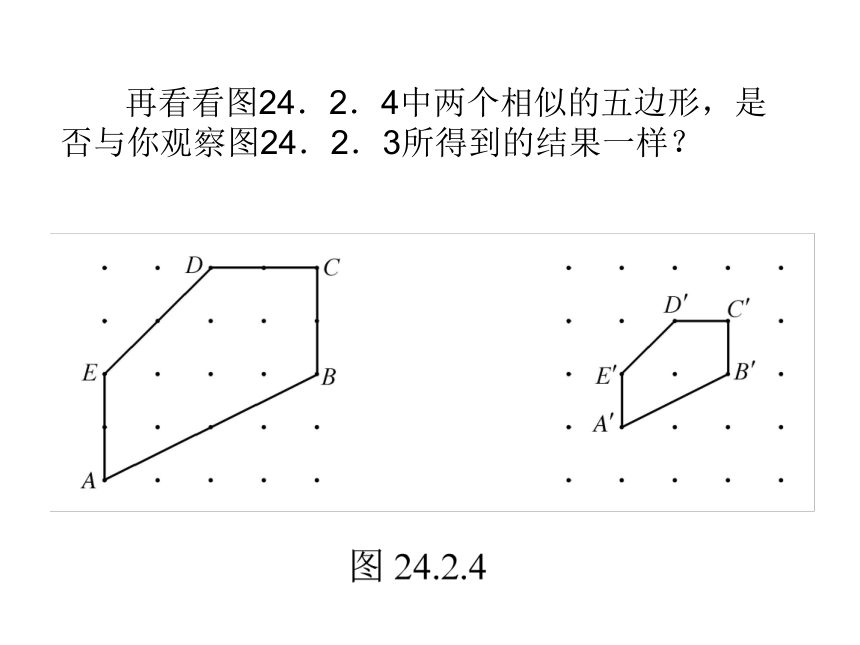
这样的结论对一般的相似多边形是否成立呢?图24.2.3中两个四边形是相似形,仔细观察这两个图形,它们的对应边之间是否有以上的关系呢?对应角之间又有什么关系? 再看看图24.2.4中两个相似的五边形,是否与你观察图24.2.3所得到的结果一样?由此可以得到两个相似多边形的性质:
归纳小结 实际上这也是我们判定两个多边形是否相似的方法,
即如果_________________________,那么这两个多边形相似.对应边成比例,对应角相等. 一般地,两个边数相同的多边形,如果它们的对应角相等,对应边长度的比相等,那么这两个多边形叫做相似多边形。
①②对应角相等对应边长度的比相等这时,对应边长度的比叫做相似比,也叫相似系数.剖析:
(1)两个多边形的边数不同一定不是相似多边形;
(2)定义中“对应角相等”、“对应边成比例”是判定 两个多边形是否相似的必备的条件,缺一不可;
(3)两个相似多边形的相似比是有顺序的.∠A=∠A1,∠B=∠B1,∠C=∠C1,23请你观察:下图的两个等边三角形有什么联系?请你观察:下图的两个正方形有什么联系?∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1; 1.53例 在图24.2.5所示的相似四边形中,求未知边x的长度和角度α的大小.分析:
利用相似多边形的性质和多边形的内角和可以解决,注意,在利用性质时,必须分清对应边和对应角。思考
两个三角形一定是相似形吗?两个等腰三角形呢?两个等边三角形呢? 针对练习1.(1)根据图示求线段比:(2)试指出图中成比例的线段. 2、 如图,菱形ABCD和菱形A1B1C1D1相似吗?为什么?分析: 对应角不相等答案:不相似。 3、如图,矩形ABCD和矩形A1B1C1D1相似吗?为什么?分析: 对应边长度的比不相等答案:不相似。4.如图所示的两个矩形是否相似?总结梳理 内化目标相似多边形角:边:对应角相等对应边长度的比相等相似比(相似系数)达标测评 反思目标1. (2014?闸北区一模)对一个图形进行放缩时,下列说法中正确的是( )
A.图形中线段的长度与角的大小都保持不变
B.图形中线段的长度与角的大小都会改变
C.图形中线段的长度保持不变、角的大小可以改变
D.图形中线段的长度可以改变、角的大小保持不变D2. (2014?江北区模拟)下面给出了一些关于相似的命题,其中真命题有( )
(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似;(5)正六边形都相似.
A.1?个 B.2个 C.3个 D.4个达标测评 反思目标C3. 下列图形中一定相似的一组是( )
A.邻边对应成比例的两个平行四边形
B.有一个内角相等的两个菱形
C.腰长对应成比例的两个等腰三角形
D.有一条边相等的两个矩形达标测评 反思目标B课堂作业P60 1,2,3,4,5
2.会利用相似图形的性质和概念进行计算和证明.? 两个相似的平面图形之间有什么关系呢?为什么有些图形是相似的,而有些不是呢?相似图形有什么主要性质呢?创设情境 明确目标合作探究 达成目标 图24.2.2是某个城市的大小不同的两张地图,当然,它们是相似的图形.设在大地图中有A、B、C三地,在小地图中的相应三地记为A′、B′、C′,试用刻度尺量一量两张地图中A(A′)与B(B′)两地之间的图上距离、B(B′)与C(C′)两地之间的图上距离.AB=______cm, BC=______cm;
A′B′=______cm, B′C′=______cm.
显然两张地图中AB和A′B′、BC和B′C′的长度都是不相等的,那么它们之间有什么关系呢?小地图是由大地图缩小得来的,我们能感到线段A′B′、B′C′与AB、BC的长度相 比都“同样程度”地缩小了. 计算可得=________,=________. 上面地图中AB、A′B′、BC、B′C′这四条线段是成比例线段.实际上,上面两张相似的地图中的对应线段都是成比例的.
这样的结论对一般的相似多边形是否成立呢?图24.2.3中两个四边形是相似形,仔细观察这两个图形,它们的对应边之间是否有以上的关系呢?对应角之间又有什么关系? 再看看图24.2.4中两个相似的五边形,是否与你观察图24.2.3所得到的结果一样?由此可以得到两个相似多边形的性质:
归纳小结 实际上这也是我们判定两个多边形是否相似的方法,
即如果_________________________,那么这两个多边形相似.对应边成比例,对应角相等. 一般地,两个边数相同的多边形,如果它们的对应角相等,对应边长度的比相等,那么这两个多边形叫做相似多边形。
①②对应角相等对应边长度的比相等这时,对应边长度的比叫做相似比,也叫相似系数.剖析:
(1)两个多边形的边数不同一定不是相似多边形;
(2)定义中“对应角相等”、“对应边成比例”是判定 两个多边形是否相似的必备的条件,缺一不可;
(3)两个相似多边形的相似比是有顺序的.∠A=∠A1,∠B=∠B1,∠C=∠C1,23请你观察:下图的两个等边三角形有什么联系?请你观察:下图的两个正方形有什么联系?∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1; 1.53例 在图24.2.5所示的相似四边形中,求未知边x的长度和角度α的大小.分析:
利用相似多边形的性质和多边形的内角和可以解决,注意,在利用性质时,必须分清对应边和对应角。思考
两个三角形一定是相似形吗?两个等腰三角形呢?两个等边三角形呢? 针对练习1.(1)根据图示求线段比:(2)试指出图中成比例的线段. 2、 如图,菱形ABCD和菱形A1B1C1D1相似吗?为什么?分析: 对应角不相等答案:不相似。 3、如图,矩形ABCD和矩形A1B1C1D1相似吗?为什么?分析: 对应边长度的比不相等答案:不相似。4.如图所示的两个矩形是否相似?总结梳理 内化目标相似多边形角:边:对应角相等对应边长度的比相等相似比(相似系数)达标测评 反思目标1. (2014?闸北区一模)对一个图形进行放缩时,下列说法中正确的是( )
A.图形中线段的长度与角的大小都保持不变
B.图形中线段的长度与角的大小都会改变
C.图形中线段的长度保持不变、角的大小可以改变
D.图形中线段的长度可以改变、角的大小保持不变D2. (2014?江北区模拟)下面给出了一些关于相似的命题,其中真命题有( )
(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似;(5)正六边形都相似.
A.1?个 B.2个 C.3个 D.4个达标测评 反思目标C3. 下列图形中一定相似的一组是( )
A.邻边对应成比例的两个平行四边形
B.有一个内角相等的两个菱形
C.腰长对应成比例的两个等腰三角形
D.有一条边相等的两个矩形达标测评 反思目标B课堂作业P60 1,2,3,4,5
