18.1勾股定理(2) 课件(共25张PPT)
文档属性
| 名称 | 18.1勾股定理(2) 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 10:26:15 | ||
图片预览



文档简介
(共25张PPT)
18.1 勾股定理 (2)
教学目标:
1.能运用勾股定理求线段长度,并解决一些简单的实际问题;
2.在利用勾股定理解决实际生活问题的过程中,能
从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长.
教学重点:
运用勾股定理计算线段长度,解决实际问题.
a
b
c
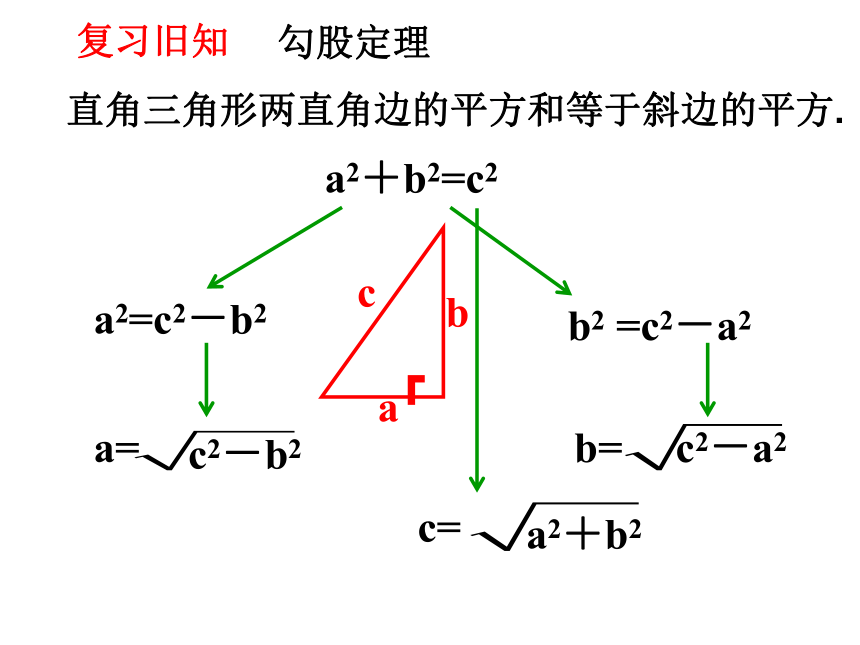
勾股定理
a2+b2=c2
a2=c2-b2
b2 =c2-a2
c=
a2+b2
a=
b=
c2-a2
c2-b2
直角三角形两直角边的平方和等于斜边的平方.
┏
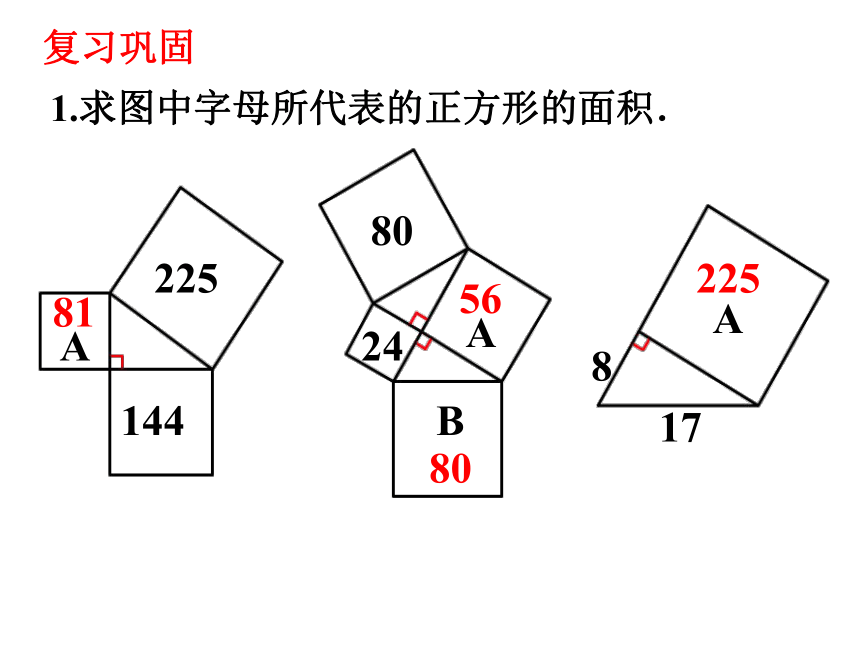
复习旧知
1.求图中字母所代表的正方形的面积.
A
A
A
B
225
144
80
24
17
8
81
56
80
225
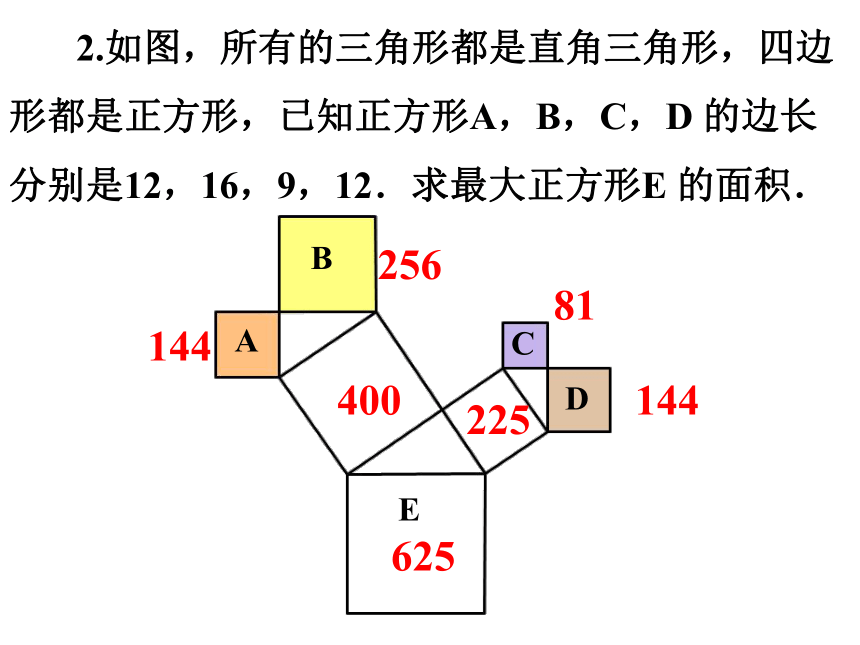
复习巩固
2.如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积.
A
B
C
D
E
400
225
625
144
256
81
144
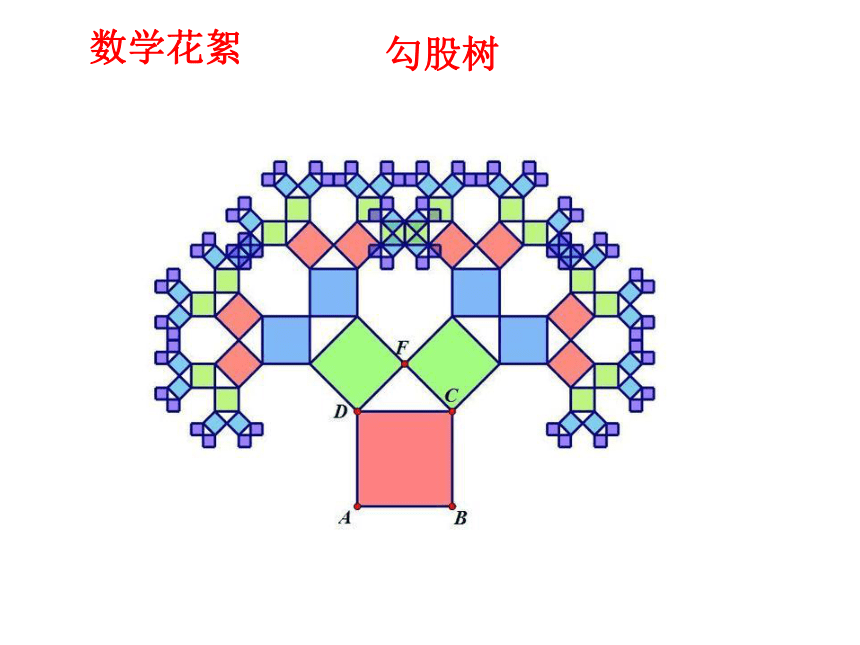
数学花絮
勾股树
数学花絮
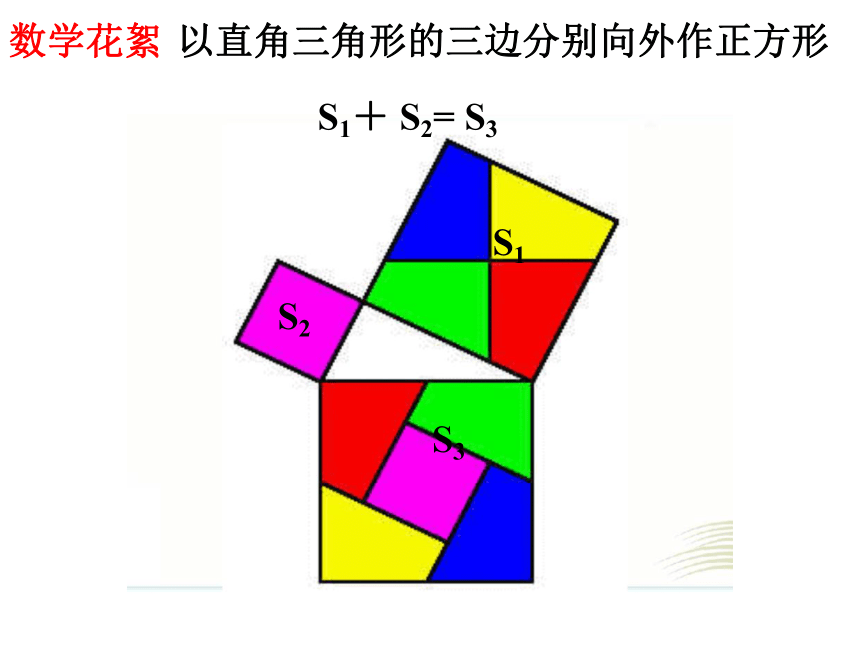
以直角三角形的三边分别向外作正方形
S1+ S2= S3
S1
S2
S3
数学花絮
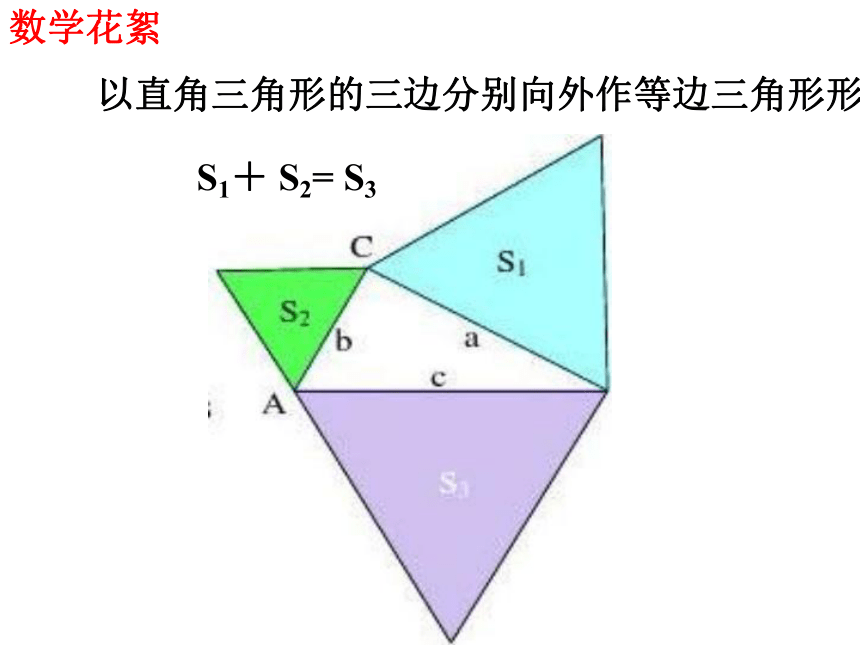
以直角三角形的三边分别向外作等边三角形形
S1+ S2= S3
数学花絮
以直角三角形的三边分别向外作正五边形
S1+ S2= S3
数学花絮
数学花絮
以直角三角形的三边分别向外作半圆
S1+ S2= S3
例1 现有一楼房发生火灾,消防队员决定用消防车的云梯救人,已知云梯最多只能伸长到10m,消防车高3m,救人时云梯伸至最长,在完成从9m高处救人后还要从12m高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到0.1米)
A
B
E
O
D
C
靠近多少米?
即AC的长
OB=?
9m
OD=?
12m
OE=?
3m
AB=?
10m
CD=?
10m
例题解析
A
B
E
O
D
C
靠近多少米?
即求AC的长
AC=?
AC=AE-EC
BE=?
DE=?
Rt△AEB
Rt△DEC
解:
在Rt△AEB中,根据勾股定理,
AE2=AB2-BE 2=102-62=64.
∴AE =
=8
64
OB-OE
OD-OE
A
B
E
O
D
C
解:
在Rt△AEB中,根据勾股定理,
AE2=AB2-BE 2=102-62=64.
∴AE =
=8
64
在Rt△CED中,根据勾股定理,
EC2=CD2-DE2=102-92=19.
∴EC =
=4.36
19
∴AC =
AE-EC
=8-4.36
≈3.6(m)
答:消防车要再靠近3.6米.
1.在Rt△ABC中,∠C=90°.
(1)如果a=6,b=8, 则c= ;
(2)如果a=8,c=17, 则b= ;
A
C
B
a
b
c
10
15
练习巩固
2.如图, 楼梯的高度为2m,楼梯坡面的长度为4m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?
地毯的长度
BC
+AC
B
A
C
2.如图, 楼梯的高度为2m,楼梯坡面的长度为4m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?
B
A
C
∴BC+AC=
解:
在Rt△ABC中,
AC2=AB2-BC2
=42-22=12.
∴AC=
12
=
3
2
2+
3
2
=2+2 × 1.73
≈5.5(m)
答:地毯的长度至少需要5.5米.
3.一个门框的尺寸如图所示,一块长3 m,
宽 2.2 m的长方形薄木板能否从门框内通过?
A
B
C
D
1 m
2 m
解:在Rt△ABC中,根据勾股定理,得
AC2=AB2+BC2
=12+22=5.
∴AC=
≈ 2.24
∵AC大于木板的宽2.2 m,
∴木板能从门框内通过.
5
练习巩固
(1)利用勾股定理解决实际问题有哪些基本步骤?
(2)你觉得解决实际问题的难点在哪里?你有什
么好的突破办法?利用勾股定理解决实际问
题的注意点是什么?请与大家交流.
(3)本节课体现出哪些数学思想方法,都在什么
情况下运用?
课堂小结
1.求下列直角三角形中未知边x的长度.
A
B
C
4
6
x
C
B
A
5
10
x
x=
42+ 62
=
52
=
2
13
x=
102-52
=
75
=
3
5
巩固提高
2.如图,在△ABC 中,∠B =90°,若BC=4 ,
AB=x ,AC=8-x,则AB= , AC= .
A
B
C
x
8-x
4
3
5
42+x2
=
( 8-x)2
16+x2
=
64-16x+x2
3.如图,一架2.6米长的梯子AB 斜靠在一竖直的墙AO上,这时AO 为2.4米.如果梯子的顶端A沿墙下滑0.5米,那么梯子底端B也外移0.5米吗?
解:
在Rt△AOB中,根据勾股定理,
OB2=AB2-OA2=2.62-2.42=1.
在Rt△COD中,根据勾股定理,
OD2=CD2-OC2
=2.62-(2. 4-0.5)2=3.15
∴OB =
=1
1
∴OD =
≈ 1.77
3.15
解:
在Rt△AOB中,根据勾股定理,
OB2=AB2-OA2=2.62-2.42=1.
在Rt△COD中,根据勾股定理,
OD2=CD2-OC2
=2.62-(2. 4-0.5)2=3.15
∴OB =
=1
1
∴OD =
≈ 1.77
3.15
∴BD =
≈ 1.77-1
OD-OB
= 0.77
∴梯子的顶端A沿墙下滑0.5米时,梯子底端B并不是也外移0.5米,而是外移约0.77米。
4. 已知:如图,在Rt△ABC中, ∠C=90° ,
两直角边和斜边的长都是正整数,其中BC的长为7.
求这个直角三角形的面积.
解:
在Rt△ABC中,根据勾股定理,
BC2=AB2-BC 2.
∴c2-b2=72,
∴(c+b)(c-b)=49.
∴ 49=1×49
=7×7
=49×1.
∵两直角边和斜边的长都是正整数,
∵c>b,
∴c+b=49,c-b=1.
∴c=25,b=24.
∴ S△ABC=
1
2
BC · AC
=
×7×24
1
2
=84.
A
7
C
B
C
今天作业
课本P57页第5、6题
18.1 勾股定理 (2)
教学目标:
1.能运用勾股定理求线段长度,并解决一些简单的实际问题;
2.在利用勾股定理解决实际生活问题的过程中,能
从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长.
教学重点:
运用勾股定理计算线段长度,解决实际问题.
a
b
c
勾股定理
a2+b2=c2
a2=c2-b2
b2 =c2-a2
c=
a2+b2
a=
b=
c2-a2
c2-b2
直角三角形两直角边的平方和等于斜边的平方.
┏
复习旧知
1.求图中字母所代表的正方形的面积.
A
A
A
B
225
144
80
24
17
8
81
56
80
225
复习巩固
2.如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积.
A
B
C
D
E
400
225
625
144
256
81
144
数学花絮
勾股树
数学花絮
以直角三角形的三边分别向外作正方形
S1+ S2= S3
S1
S2
S3
数学花絮
以直角三角形的三边分别向外作等边三角形形
S1+ S2= S3
数学花絮
以直角三角形的三边分别向外作正五边形
S1+ S2= S3
数学花絮
数学花絮
以直角三角形的三边分别向外作半圆
S1+ S2= S3
例1 现有一楼房发生火灾,消防队员决定用消防车的云梯救人,已知云梯最多只能伸长到10m,消防车高3m,救人时云梯伸至最长,在完成从9m高处救人后还要从12m高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到0.1米)
A
B
E
O
D
C
靠近多少米?
即AC的长
OB=?
9m
OD=?
12m
OE=?
3m
AB=?
10m
CD=?
10m
例题解析
A
B
E
O
D
C
靠近多少米?
即求AC的长
AC=?
AC=AE-EC
BE=?
DE=?
Rt△AEB
Rt△DEC
解:
在Rt△AEB中,根据勾股定理,
AE2=AB2-BE 2=102-62=64.
∴AE =
=8
64
OB-OE
OD-OE
A
B
E
O
D
C
解:
在Rt△AEB中,根据勾股定理,
AE2=AB2-BE 2=102-62=64.
∴AE =
=8
64
在Rt△CED中,根据勾股定理,
EC2=CD2-DE2=102-92=19.
∴EC =
=4.36
19
∴AC =
AE-EC
=8-4.36
≈3.6(m)
答:消防车要再靠近3.6米.
1.在Rt△ABC中,∠C=90°.
(1)如果a=6,b=8, 则c= ;
(2)如果a=8,c=17, 则b= ;
A
C
B
a
b
c
10
15
练习巩固
2.如图, 楼梯的高度为2m,楼梯坡面的长度为4m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?
地毯的长度
BC
+AC
B
A
C
2.如图, 楼梯的高度为2m,楼梯坡面的长度为4m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?
B
A
C
∴BC+AC=
解:
在Rt△ABC中,
AC2=AB2-BC2
=42-22=12.
∴AC=
12
=
3
2
2+
3
2
=2+2 × 1.73
≈5.5(m)
答:地毯的长度至少需要5.5米.
3.一个门框的尺寸如图所示,一块长3 m,
宽 2.2 m的长方形薄木板能否从门框内通过?
A
B
C
D
1 m
2 m
解:在Rt△ABC中,根据勾股定理,得
AC2=AB2+BC2
=12+22=5.
∴AC=
≈ 2.24
∵AC大于木板的宽2.2 m,
∴木板能从门框内通过.
5
练习巩固
(1)利用勾股定理解决实际问题有哪些基本步骤?
(2)你觉得解决实际问题的难点在哪里?你有什
么好的突破办法?利用勾股定理解决实际问
题的注意点是什么?请与大家交流.
(3)本节课体现出哪些数学思想方法,都在什么
情况下运用?
课堂小结
1.求下列直角三角形中未知边x的长度.
A
B
C
4
6
x
C
B
A
5
10
x
x=
42+ 62
=
52
=
2
13
x=
102-52
=
75
=
3
5
巩固提高
2.如图,在△ABC 中,∠B =90°,若BC=4 ,
AB=x ,AC=8-x,则AB= , AC= .
A
B
C
x
8-x
4
3
5
42+x2
=
( 8-x)2
16+x2
=
64-16x+x2
3.如图,一架2.6米长的梯子AB 斜靠在一竖直的墙AO上,这时AO 为2.4米.如果梯子的顶端A沿墙下滑0.5米,那么梯子底端B也外移0.5米吗?
解:
在Rt△AOB中,根据勾股定理,
OB2=AB2-OA2=2.62-2.42=1.
在Rt△COD中,根据勾股定理,
OD2=CD2-OC2
=2.62-(2. 4-0.5)2=3.15
∴OB =
=1
1
∴OD =
≈ 1.77
3.15
解:
在Rt△AOB中,根据勾股定理,
OB2=AB2-OA2=2.62-2.42=1.
在Rt△COD中,根据勾股定理,
OD2=CD2-OC2
=2.62-(2. 4-0.5)2=3.15
∴OB =
=1
1
∴OD =
≈ 1.77
3.15
∴BD =
≈ 1.77-1
OD-OB
= 0.77
∴梯子的顶端A沿墙下滑0.5米时,梯子底端B并不是也外移0.5米,而是外移约0.77米。
4. 已知:如图,在Rt△ABC中, ∠C=90° ,
两直角边和斜边的长都是正整数,其中BC的长为7.
求这个直角三角形的面积.
解:
在Rt△ABC中,根据勾股定理,
BC2=AB2-BC 2.
∴c2-b2=72,
∴(c+b)(c-b)=49.
∴ 49=1×49
=7×7
=49×1.
∵两直角边和斜边的长都是正整数,
∵c>b,
∴c+b=49,c-b=1.
∴c=25,b=24.
∴ S△ABC=
1
2
BC · AC
=
×7×24
1
2
=84.
A
7
C
B
C
今天作业
课本P57页第5、6题
