沪科版八年级下册18.1勾股定理 课件(共21张PPT)
文档属性
| 名称 | 沪科版八年级下册18.1勾股定理 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
18.1 勾股定理 (3)
教学目标:
1.能应用勾股定理在数轴上画出表示无理数的点;
2.体会勾股定理在数学中的地位和作用.
教学重点:
用勾股定理作出长度为无理数的线段.
a
b
c
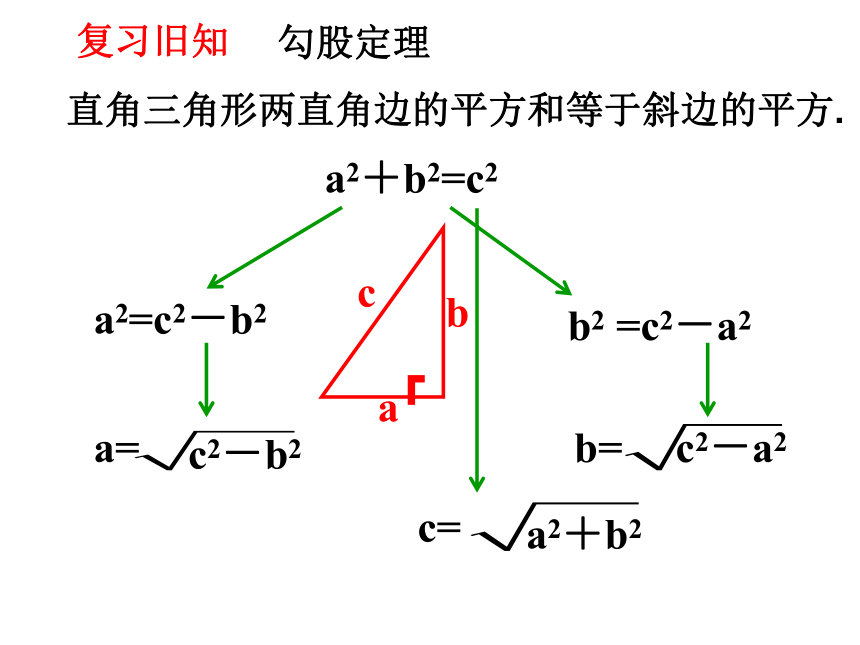
勾股定理
a2+b2=c2
a2=c2-b2
b2 =c2-a2
c=
a2+b2
a=
b=
c2-a2
c2-b2
直角三角形两直角边的平方和等于斜边的平方.
┏
复习旧知
1.在Rt△ABC中∠C=90°, ∠A=30°,b=3,
则a= , c= .
A
C
B
a
b
c
x
2x
∴3x2=9
(2x) 2-x2
32
=
∴x2 = 3
∴x=
3
3
3
2
复习巩固
2.在Rt△ABC中,已知a=4,b=3,则第三边c的长为 .
5
或
7
复习巩固
例2 已知:如图,在Rt△ABC中,两直角边AC=5,BC=12,求斜边上的高CD的长.
A
D
C
B
C
解:在Rt△ABC中,
AB2=AC2+BC2
∴AB =
=13
169
又∵S△ ABC =
1
2
BC · AC
=
1
2
AB · CD
=52+122=169.
∴CD =
BC · AC
AB
=
5 × 12
13
=
60
13
例题解析
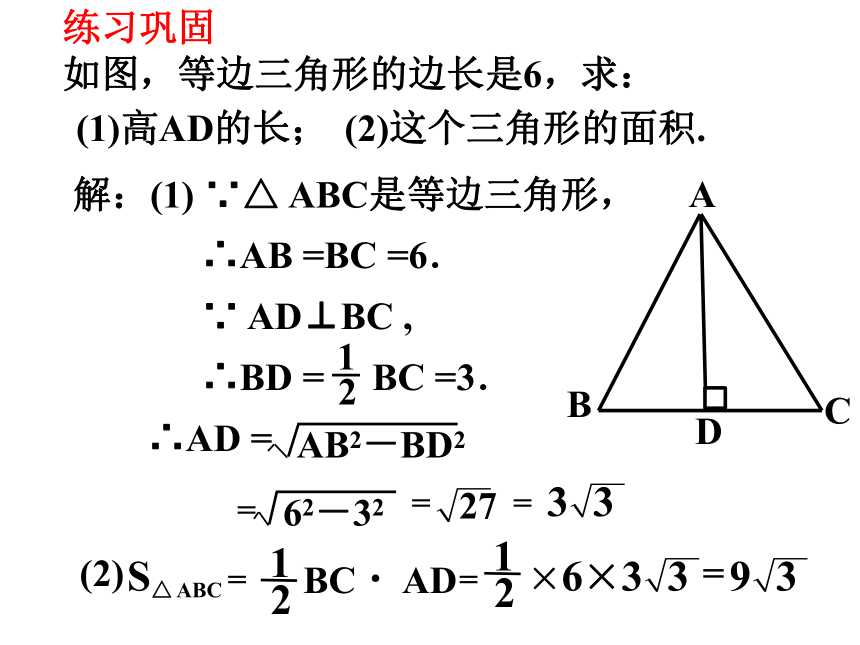
如图,等边三角形的边长是6,求:
(1)高AD的长;
(2)这个三角形的面积.
A
B
C
D
解:(1) ∵△ ABC是等边三角形,
∴AB =BC =6.
∵ AD⊥BC ,
∴BD = BC =3.
∴AD =
AB2-BD2
=
62-32
=
27
=
(2)
3
3
S△ ABC =
●
1
2
1
2
1
2
=
3
3
BC AD
= ×6×
3
9
练习巩固
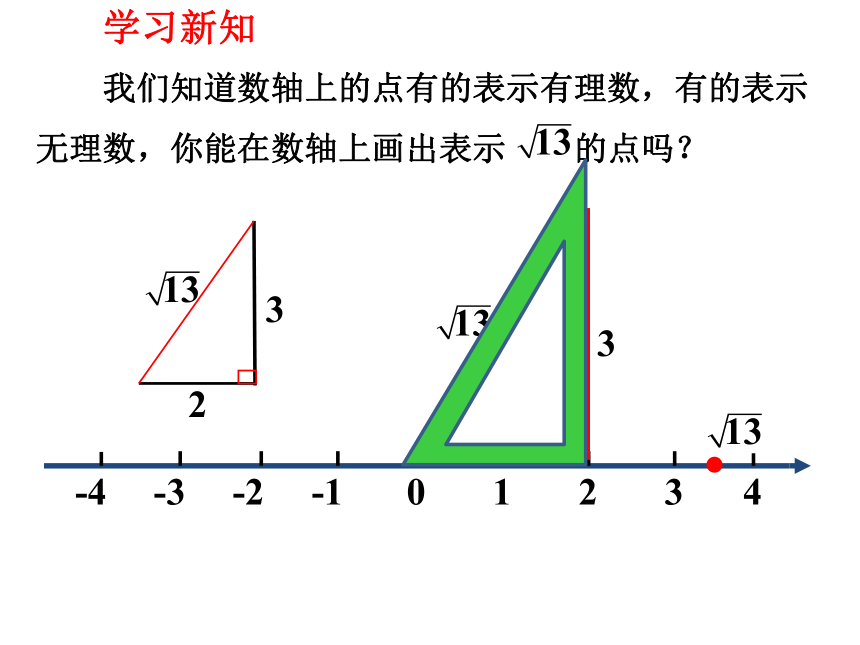
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
13
2
3
13
0
1
2
3
-1
-2
-3
-4
4
3
13
13
学习新知
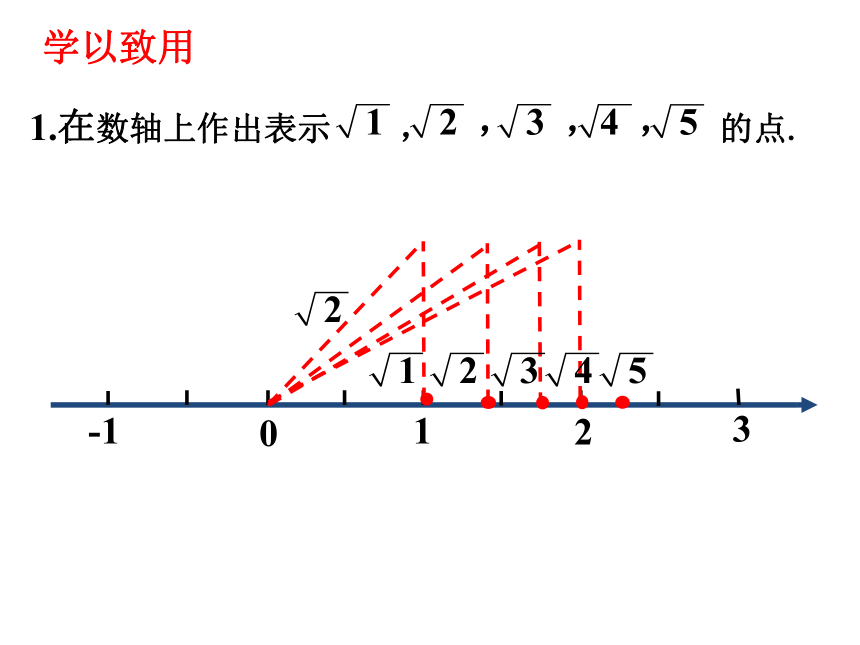
1.在数轴上作出表示 , 的点.
1
1
2
0
-1
3
1
2
2 ,
3 ,
4 ,
5
3
2
4
5
学以致用
2.在数轴上作出表示 的点.
17
2
3
4
5
1
0
-1
-2
6
1
17
17
解:
学以致用
“数学海螺”
数学花絮
海螺
数学花絮
“数学海螺”
数学花絮
银河系旋转图
数学花絮
(1)勾股定理有哪些方面的应用,本节课学习了
勾股定理哪几方面的应用?
(2)你能说说勾股定理求线段长的基本思路吗?
(3)本节课体现出哪些数学思想方法?
课堂小结
1.如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处.已知BC=12,∠B=30°,则DE的长是( ).
A.6 B.4 C.3 D.2
A
B
C
D
E
B
x
2x
x
巩固提高
2.如图,△ACB和△ECD都是等腰直角三角形, ∠ACB =∠ECD =90°,D为AB边上一点.求证:AD2 +DB2 =DE2.
A
B
C
D
E
要证:AD2 +DB2 =DE2
要证:AD2 +AE2 =DE2
要证:AE=BD,
要证:△ACE≌△BCD.
要证:∠ACE =∠BCD.
∠EAD =90°.
∴ ∠DAE =∠CAE+∠BA C=
∴ AD2 +AE2 =DE2.
证明:∵ ∠BCD +∠ACD =∠ACB =90°
∴∠BCD =∠ACE.
∵ BC=AC, DC=EC,
∴△ACE≌△BCD.
∴AD2 +DB2 =DE2.
A
B
C
D
E
∠ACE +∠ACD =∠ECD =90°
∴AE=BD,
∠EAC =∠B =45°.
∠EAC +∠B =90°.
3.如图,△ABC的三个顶点坐标分别为A(0,2),B(4,0),C(6,4),求△ABC的周长与面积.
A
B
C
O
y
x
1
6
5
1
解:
∵ A(0,2),B(4,0),C(6,4),
∴AB2= OA2+OB2
∴AB=
=22+42
=20
20
=2
5
∵BC2= 22+42
=20
AC2= 22+62
=40
∴BC=
20
=2
5
AC=
40
=2
10
∴L△ABC =AB
+BC+AC
=4
5
+
2
10
3.如图,△ABC的三个顶点坐标分别为A(0,2),B(4,0),C(6,4),求△ABC的周长与面积.
A
B
C
O
y
x
1
6
5
1
解:
S△ABC =6×4
-
×2×4
1
2
-
×2×4
1
2
-
×2×6
1
2
=10
今天作业
课本P57页第4、7题
18.1 勾股定理 (3)
教学目标:
1.能应用勾股定理在数轴上画出表示无理数的点;
2.体会勾股定理在数学中的地位和作用.
教学重点:
用勾股定理作出长度为无理数的线段.
a
b
c
勾股定理
a2+b2=c2
a2=c2-b2
b2 =c2-a2
c=
a2+b2
a=
b=
c2-a2
c2-b2
直角三角形两直角边的平方和等于斜边的平方.
┏
复习旧知
1.在Rt△ABC中∠C=90°, ∠A=30°,b=3,
则a= , c= .
A
C
B
a
b
c
x
2x
∴3x2=9
(2x) 2-x2
32
=
∴x2 = 3
∴x=
3
3
3
2
复习巩固
2.在Rt△ABC中,已知a=4,b=3,则第三边c的长为 .
5
或
7
复习巩固
例2 已知:如图,在Rt△ABC中,两直角边AC=5,BC=12,求斜边上的高CD的长.
A
D
C
B
C
解:在Rt△ABC中,
AB2=AC2+BC2
∴AB =
=13
169
又∵S△ ABC =
1
2
BC · AC
=
1
2
AB · CD
=52+122=169.
∴CD =
BC · AC
AB
=
5 × 12
13
=
60
13
例题解析
如图,等边三角形的边长是6,求:
(1)高AD的长;
(2)这个三角形的面积.
A
B
C
D
解:(1) ∵△ ABC是等边三角形,
∴AB =BC =6.
∵ AD⊥BC ,
∴BD = BC =3.
∴AD =
AB2-BD2
=
62-32
=
27
=
(2)
3
3
S△ ABC =
●
1
2
1
2
1
2
=
3
3
BC AD
= ×6×
3
9
练习巩固
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
13
2
3
13
0
1
2
3
-1
-2
-3
-4
4
3
13
13
学习新知
1.在数轴上作出表示 , 的点.
1
1
2
0
-1
3
1
2
2 ,
3 ,
4 ,
5
3
2
4
5
学以致用
2.在数轴上作出表示 的点.
17
2
3
4
5
1
0
-1
-2
6
1
17
17
解:
学以致用
“数学海螺”
数学花絮
海螺
数学花絮
“数学海螺”
数学花絮
银河系旋转图
数学花絮
(1)勾股定理有哪些方面的应用,本节课学习了
勾股定理哪几方面的应用?
(2)你能说说勾股定理求线段长的基本思路吗?
(3)本节课体现出哪些数学思想方法?
课堂小结
1.如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处.已知BC=12,∠B=30°,则DE的长是( ).
A.6 B.4 C.3 D.2
A
B
C
D
E
B
x
2x
x
巩固提高
2.如图,△ACB和△ECD都是等腰直角三角形, ∠ACB =∠ECD =90°,D为AB边上一点.求证:AD2 +DB2 =DE2.
A
B
C
D
E
要证:AD2 +DB2 =DE2
要证:AD2 +AE2 =DE2
要证:AE=BD,
要证:△ACE≌△BCD.
要证:∠ACE =∠BCD.
∠EAD =90°.
∴ ∠DAE =∠CAE+∠BA C=
∴ AD2 +AE2 =DE2.
证明:∵ ∠BCD +∠ACD =∠ACB =90°
∴∠BCD =∠ACE.
∵ BC=AC, DC=EC,
∴△ACE≌△BCD.
∴AD2 +DB2 =DE2.
A
B
C
D
E
∠ACE +∠ACD =∠ECD =90°
∴AE=BD,
∠EAC =∠B =45°.
∠EAC +∠B =90°.
3.如图,△ABC的三个顶点坐标分别为A(0,2),B(4,0),C(6,4),求△ABC的周长与面积.
A
B
C
O
y
x
1
6
5
1
解:
∵ A(0,2),B(4,0),C(6,4),
∴AB2= OA2+OB2
∴AB=
=22+42
=20
20
=2
5
∵BC2= 22+42
=20
AC2= 22+62
=40
∴BC=
20
=2
5
AC=
40
=2
10
∴L△ABC =AB
+BC+AC
=4
5
+
2
10
3.如图,△ABC的三个顶点坐标分别为A(0,2),B(4,0),C(6,4),求△ABC的周长与面积.
A
B
C
O
y
x
1
6
5
1
解:
S△ABC =6×4
-
×2×4
1
2
-
×2×4
1
2
-
×2×6
1
2
=10
今天作业
课本P57页第4、7题
