2.2 圆的对称性

§2.2圆的对称性
【知识点总结】
圆的对称性
圆是中心对称图形，圆心是对称中心
圆是由旋转不变性，即圆围绕圆心旋转任何角度后，仍然与原来的圆重合
圆是轴对称图形，过圆心的任意一条直线都是它的对称轴
例1：如图是由一个圆和一个平行四边形组成的图形，要求画出一条直线，把圆与平行四边形的面积平分，应如何分割？请保留作图痕迹.【来源：21cnj*y.co*m】
二、圆心角、弧、弦之间的关系
在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都相等.可简称为“等对等定理”或“三个概念的相等关系”
例2：如图，AB、DE是⊙O的直径，C是⊙O上的一点，=弧CE，请探求并至少写出图中三对具有相等关系的量（除对顶角和半圆相等外）【出处：21教育名师】
圆心角的度数与它所对的弧的度数关系
1°的圆心角所对的弧叫做1°的弧.一般地，n°的圆心角对着的n°的弧，n°的弧对着n°的圆心角.
圆心角的度数与它所对的弧的度数相等.
例3：如图，在⊙O中，半径OC⊥AB，∠OAB=50°，求弧BC的度数.
垂径定理
垂直于弦的直径平分这条弦，并且平方弦所对的弧.
推广：一条直线：①过圆心；②垂直于弦；③平分弦（不是直径）；④平分弦所对的优弧；⑤平分弦所对的劣弧，只要具备其中两个条件，就能推出其他三个.
例4：如图，⊙O的弦AB垂直平分半径OC，若,则⊙O的半径为
【典例展示】
题型一 概念辨析题
例1：下列说法：①圆是轴对称图形，每条直径都是它的对称轴；②垂直于弦的直线平分这条弦；③平分弦的直径垂直于这条弦；④在同圆或等圆中，如果两条弦相等，那么它们所对的两条弧也相等，其中，不正确的有（ ）21·cn·jy·com
A.1个 B.2个 C.3个 D.4个21·世纪*教育网
题型二 简单计算题
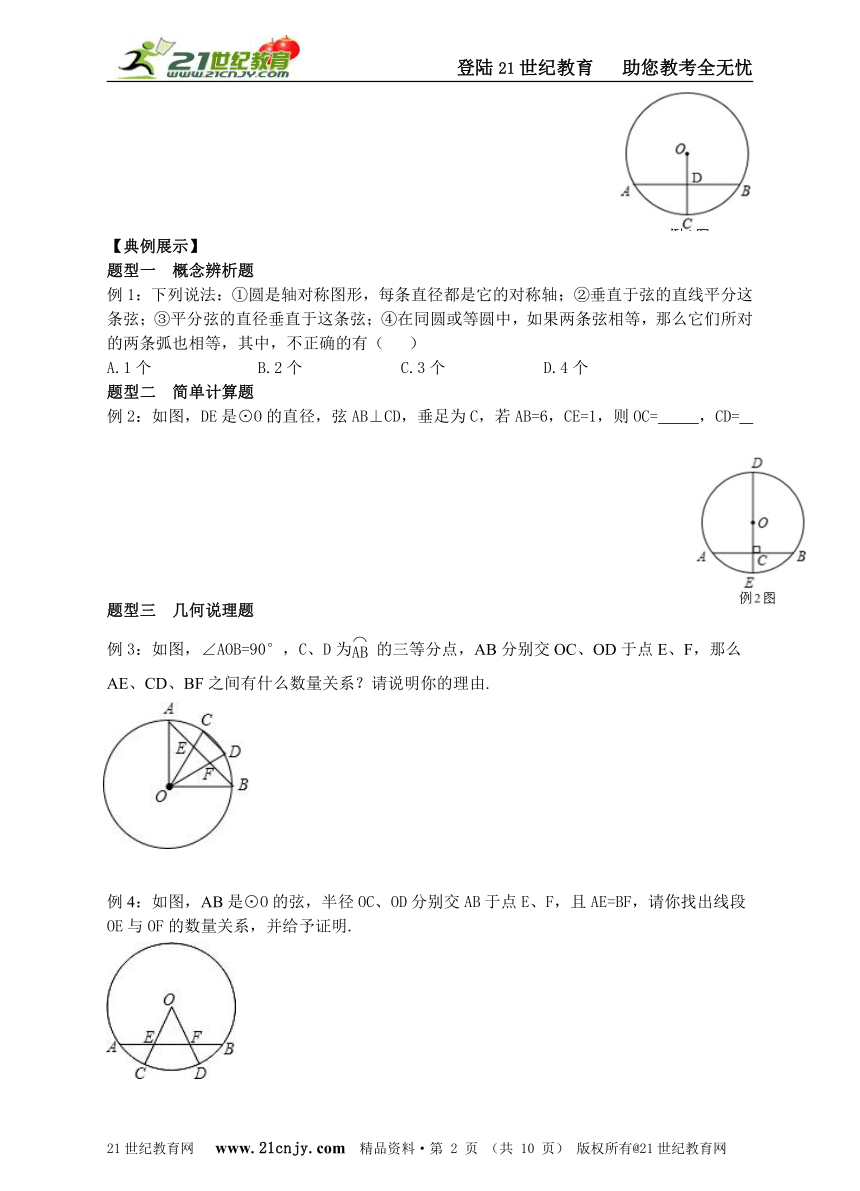
例2：如图，DE是⊙O的直径，弦AB⊥CD，垂足为C，若AB=6，CE=1，则OC= ，CD=
题型三 几何说理题
例3：如图，∠AOB=90°，C、D为的三等分点，AB分别交OC、OD于点E、F，那么AE、CD、BF之间有什么数量关系？请说明你的理由.21教育名师原创作品
例4：如图，AB是⊙O的弦，半径OC、OD分别交AB于点E、F，且AE=BF，请你找出线段OE与OF的数量关系，并给予证明.21*cnjy*com
题型四 作图题
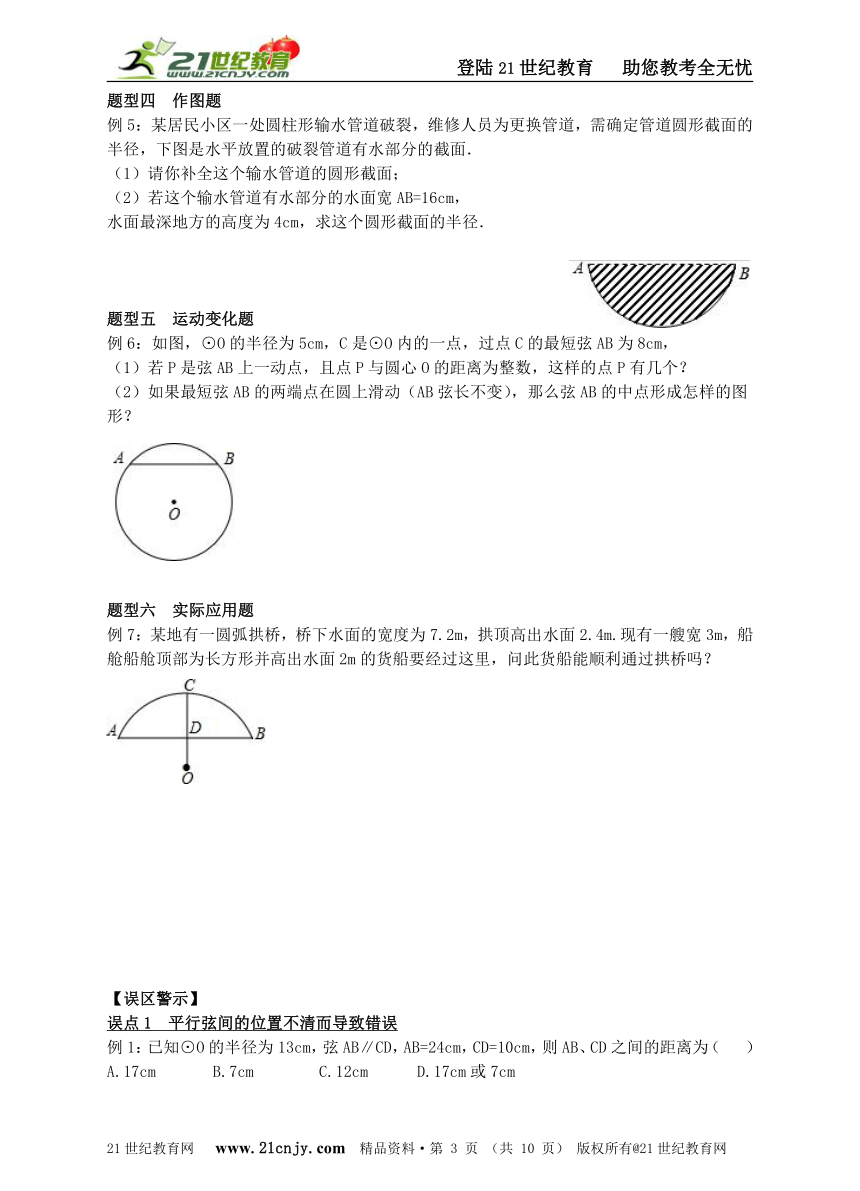
例5：某居民小区一处圆柱形输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．
（1）请你补全这个输水管道的圆形截面；
（2）若这个输水管道有水部分的水面宽AB=16cm，
水面最深地方的高度为4cm，求这个圆形截面的半径．
题型五 运动变化题
例6：如图，⊙O的半径为5cm，C是⊙O内的一点，过点C的最短弦AB为8cm，
若P是弦AB上一动点，且点P与圆心O的距离为整数，这样的点P有几个？
如果最短弦AB的两端点在圆上滑动（AB弦长不变），那么弦AB的中点形成怎样的图形？
题型六 实际应用题
例7：某地有一圆弧拱桥，桥下水面的宽度为7.2m，拱顶高出水面2.4m.现有一艘宽3m，船舱船舱顶部为长方形并高出水面2m的货船要经过这里，问此货船能顺利通过拱桥吗？
【误区警示】
误点1 平行弦间的位置不清而导致错误
例1：已知⊙O的半径为13cm，弦AB∥CD，AB=24cm，CD=10cm，则AB、CD之间的距离为（ ）
A.17cm B.7cm C.12cm D.17cm或7cm
误点2 不能正确理解圆心角、弧与弦之间的关系
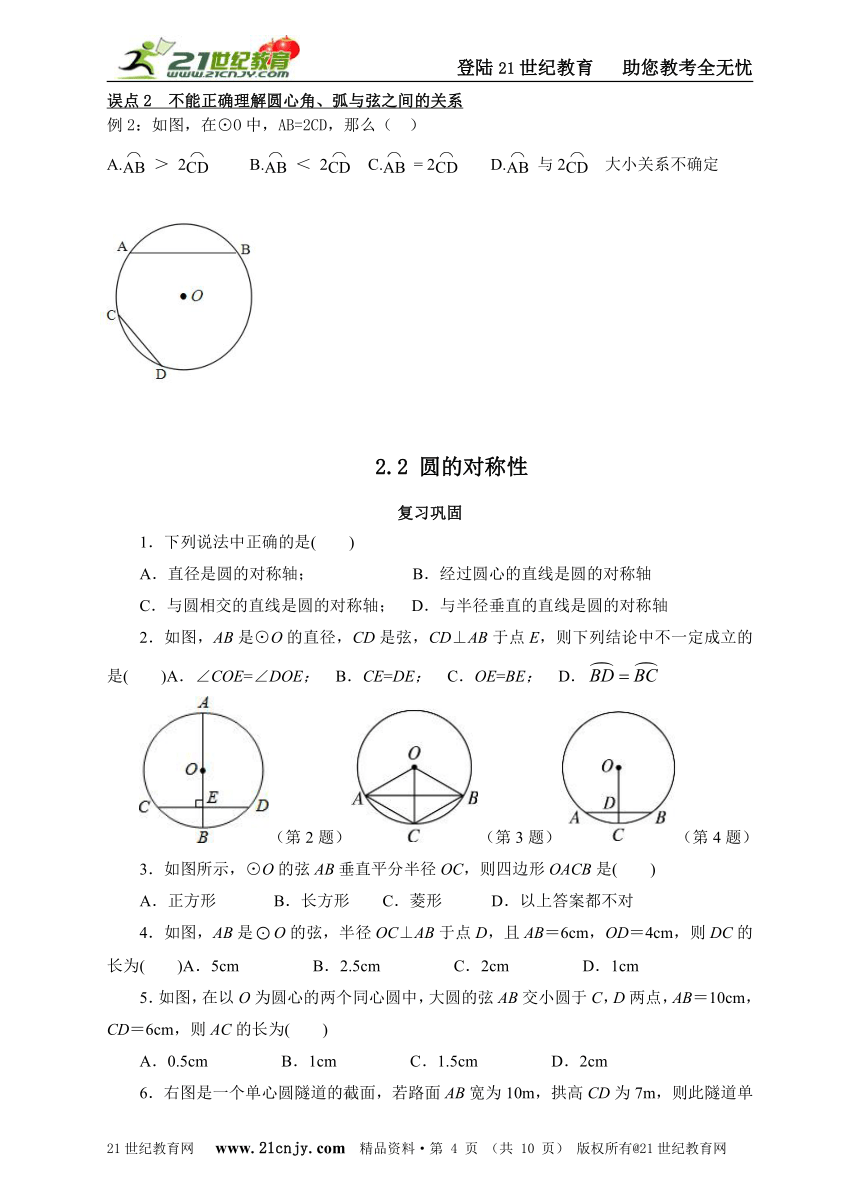
例2：如图，在⊙O中，AB=2CD，那么（ ）
A.＞ 2 B.＜ 2 C.= 2 D.与2 大小关系不确定

2.2 圆的对称性
复习巩固
1．下列说法中正确的是(　　)
A．直径是圆的对称轴； B．经过圆心的直线是圆的对称轴
C．与圆相交的直线是圆的对称轴； D．与半径垂直的直线是圆的对称轴
2．如图，AB是⊙O的直径，CD是弦，CD⊥AB于点E，则下列结论中不一定成立的是(　　)A．∠COE=∠DOE； B．CE=DE； C．OE=BE； D．
（第2题）（第3题）（第4题）
3．如图所示，⊙O的弦AB垂直平分半径OC，则四边形OACB是(　　)
A．正方形 B．长方形 C．菱形 D．以上答案都不对
4．如图，AB是O的弦，半径OC⊥AB于点D，且AB＝6cm，OD＝4cm，则DC的长为(　　)A．5cm B．2.5cm C．2cm D．1cm
5．如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点，AB＝10cm，CD＝6cm，则AC的长为(　　)21cnjy.com
A．0.5cm B．1cm C．1.5cm D．2cm
6．右图是一个单心圆隧道的截面，若路面AB宽为10m，拱高CD为7m，则此隧道单心圆的半径OA是(　　)www-2-1-cnjy-com
A．5m B．m C． m D．7m
7．已知⊙O中，弦AB的长为6cm，圆心O到弦AB的距离为4cm，则O的直径为__________cm
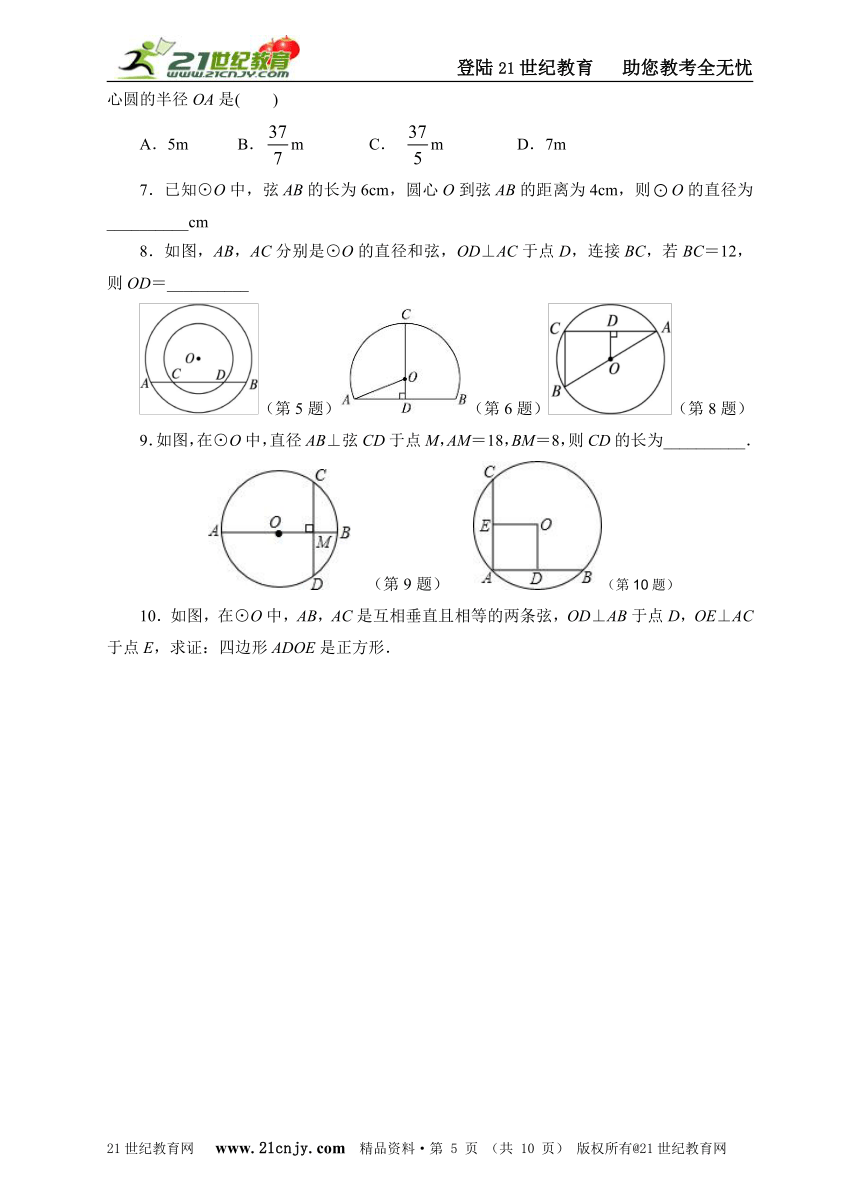
8．如图，AB，AC分别是⊙O的直径和弦，OD⊥AC于点D，连接BC，若BC＝12，则OD＝__________
（第5题）（第6题）（第8题）
9．如图，在⊙O中，直径AB⊥弦CD于点M，AM＝18，BM＝8，则CD的长为__________．
（第9题） （第10题）
10．如图，在⊙O中，AB，AC是互相垂直且相等的两条弦，OD⊥AB于点D，OE⊥AC于点E，求证：四边形ADOE是正方形．【版权所有：21教育】
能力提升
11．如图，已知⊙O的半径为5，弦AB=6，M是AB上任意一点，则线段OM的长可能是(　　) A．2.5 B．3.5 C．4.5 D．5.5
12．如图，以点P为圆心的圆弧与x轴交于A，B两点，若点P的坐标为(4,2)，点A的坐标为(2,0)，则点B的坐标为__________． 21世纪教育网版权所有
13．在半径为5cm的圆内有两条平行弦，一条弦长为8cm，另一条弦长为6cm，则两弦之间的距离为__________．www.21-cn-jy.com
14．在直径为650mm的圆柱形油桶内装进一些油后，其截面如图所示，若油面宽为600mm，求油的最大深度．2·1·c·n·j·y
15．有一座弧形的拱桥，桥下的水面宽度为7.2m，拱顶高出水面2.4m，现有一艘宽3m，船舱顶部为长方形并高出水面2m的货船要经过这里，此货船能顺利通过这座拱形桥吗？
参考答案
复习巩固
1．B　2.C
3．C　由垂径定理知AB也被OC平分，所以AB和OC互相垂直平分，即四边形OACB为菱形．
4．D　连接OB.∵OC⊥AB，AB＝6cm，
∴BD＝AB＝3cm.
∴OB＝＝5(cm)．
∴OC＝OB＝5cm.∴DC＝OC－OD＝5－4＝1(cm)．
5．D如图，过O作OE⊥AB于点E，由垂径定理，得AE＝AB＝×10＝5(cm)，CE＝CD＝×6＝3(cm)．2-1-c-n-j-y
所以AC＝AE－CE＝5－3＝2(cm)．
6．B　根据题意，得AD＝DB.
所以AD＝5m，OD＝CD－OC＝7－OA.
在Rt△ADO中，OA2＝AD2＋OD2，
即OA2＝52＋(7－OA)2，解得OA＝m.
7．10　8．6
9．24　连接OD，∵AM＝18，BM＝8，
∴OD＝＝13.
∴OM＝13－8＝5.
在Rt△ODM中，.
∵直径AB⊥弦CD，∴CD＝2DM＝2×12＝24.
10．证明：∵OE⊥AC，OD⊥AB，AB⊥AC，
∴∠OEA＝90°，∠EAD＝90°，∠ODA＝90°.
∴四边形ADOE为矩形．
由垂径定理，得AE＝AC，AD＝AB.
又AC＝AB，∴AE＝AD.
∴四边形ADOE为正方形．
能力提升
11．C　如图，过点O作OC⊥AB于点C，连接OA，则由垂径定理得AC＝AB＝3.在Rt△OAC中，由勾股定理得OC＝＝4，∵OC≤OM≤OA，即4≤OM≤5，∴线段OM的长可能是4.5.故选C. 21教育网
12．(6,0)　过点P作PC⊥AB于点C，
∵AC＝BC＝OC－OA＝4－2＝2，
∴OB＝OC＋BC＝4＋2＝6.
∴点B的坐标为(6,0)．
13．1cm或7cm　已知两条平行弦的长，求两弦之间的距离，这两条弦可能在圆心的同侧也可能在圆心的两侧(如图所示)，因此应分两种情况讨论．
∴MN＝OM－ON＝1(cm)．
故当两弦在圆心的同侧时，两弦之间的距离为1cm.
(2)当两弦在圆心的两侧时，如图②，作OM⊥AB于点M，延长MO交CD于点N.
∵AB∥CD，∴MN⊥CD.∴MN即为所求的距离．
同样地，可以求出OM＝4cm，ON＝3cmm
∴MN＝OM＋ON＝4＋3＝7(cm)．
故当两弦在圆心的两侧时，两弦之间的距离为7cm.
14．解：作OD⊥AB，交O于点D，垂足为点C，连接AO.
∵OD⊥AB，OD为半径，
∴AC＝BC＝AB＝×600＝300(mm)．
在Rt△AOC中，
(mm)，
因此CD＝OD－OC＝325－125＝200(mm)．
故油的最大深度为200mm.
15．解：判断货船能否顺利通过这座拱桥，关键是看船舱顶部两角是否会被拱桥顶部挡住．如图所示，用表示拱桥，计算出FN的长度，若FN＞2m，则货船可以顺利通过这座拱桥；否则，货船不能顺利通过这座拱桥．【来源：21·世纪·教育·网】
设拱桥的圆心为O，连接OA，OB，作OD⊥AB于点D，交于点C，交MN于点H，由垂径定理可知，D为AB的中点．　　21*cnjy*com