2.4 圆周角

§2.4圆周角
【知识点总结】
圆周角的概念
顶点在圆上，并且两边都相交的角的叫做圆周角
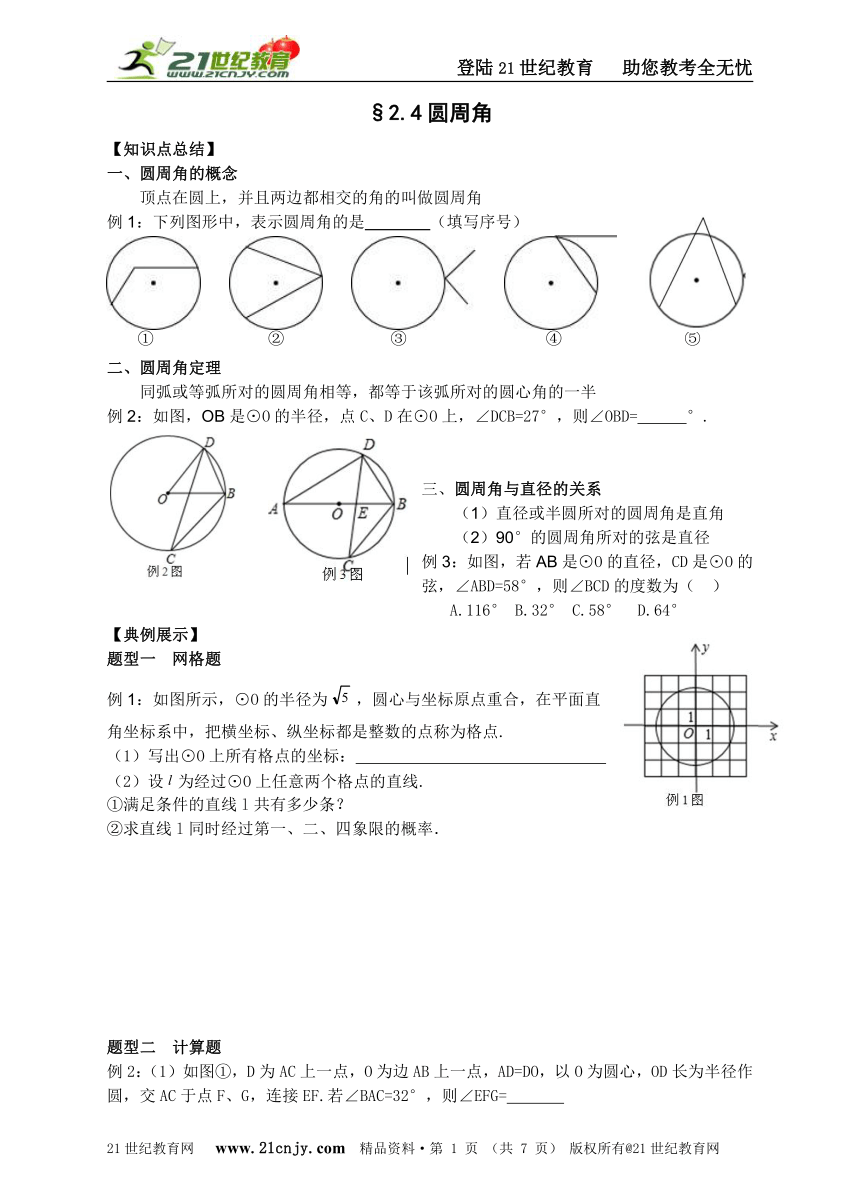
例1：下列图形中，表示圆周角的是 （填写序号）

圆周角定理
同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半
例2：如图，OB是⊙O的半径，点C、D在⊙O上，∠DCB=27°，则∠OBD= °.
三、圆周角与直径的关系
（1）直径或半圆所对的圆周角是直角
（2）90°的圆周角所对的弦是直径
例3：如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD的度数为（ ）
A.116° B.32° C.58° D.64°
【典例展示】
题型一 网格题
例1：如图所示，⊙O的半径为，圆心与坐标原点重合，在平面直角坐标系中，把横坐标、纵坐标都是整数的点称为格点.21·cn·jy·com
写出⊙O上所有格点的坐标：
设为经过⊙O上任意两个格点的直线.
①满足条件的直线l共有多少条？②求直线l同时经过第一、二、四象限的概率．
题型二 计算题
例2：（1）如图①，D为AC上一点，O为边AB上一点，AD=DO，以O为圆心，OD长为半径作圆，交AC于点F、G，连接EF.若∠BAC=32°，则∠EFG= 【来源：21·世纪·教育·网】
（2）如图②，ABC内接于⊙O，若∠B=30°，AC=，则⊙O半径为 .

题型三 探究题
例3：如图，点A、B、D、E在圆上，弦AE的延长线于弦BD的延长线交于点C.给出下列三个条件：（1）AB是圆的直径；（2）D是BC的中点；（3）AB=AC．请在上述条件中选择两个作为已知条件，第三个作为结论，写出一个你认为正确的命题，并加以证明． 21·世纪*教育网
例4：如图，A、B、C三点都在⊙O上，BE是⊙O的直径，AD是△ABC的高.
（1）现在不添加任何线或角的情况下，图中除直角外，还有相等的角吗？如果有，请写出来并加以说明；没有请说明理由（2）如果⊙O的半径R=4cm，AD=6cm，求AB·AC的值2-1-c-n-j-y

题型四 操作探索题
例5：如图∠APC的顶点在圆外，两边与圆相交，称它为圆外角.
请你按以下步骤操作：
①在图①内，连接OA、OD；
②用量角器测出下列各角的度数.
∠APC= ，∠AOC= ,
∠DOE= .(精确到1°)
根据上面的数据猜想：∠APC与∠AOC、∠DOE之间有什么数量关系？
证明你的猜想；
如图②、③，若点O不在PC上，则（2）的结论成立吗？请说明理由.
用语言描述你的发现.
题型五 学科内综合题
例6：如图，在锐角△ABC中，AC是最短边，以AC中点C为圆心，长为半径作⊙O，交BC于点E，过O作OD∥BC交⊙O于点D，连接AE、AD、DC.　　21*cnjy*com
【误区警示】
误点1 忽视圆心角，圆周角2倍关系的前提
例1：如图，在⊙O中，AB、AC是弦，O在∠BAC的内部，∠AOB=α，∠AOC=β，∠BOC=θ，下列关系式中正确的是（ ）【来源：21cnj*y.co*m】
A.θ=α+β B.θ=2α+2β C.α+β+θ=180° D.α+β+θ=360°

误点2 忽视圆中不是直径的弦所对的圆周角有两种类型
例2：如果圆的弦等于半径，那么这条弦所对的圆周角的度数等于
2.4 圆周角
复习巩固
1．如图，⊙O是△ABC的外接圆，连接OB，OC，若OB＝BC，则∠BAC等于(　　)
A．60° B．45° C．30° D．20°
2．如图，已知CD是⊙O的直径，过点D的弦DE平行于半径OA，若∠D＝50°，则∠C＝(　　)
A．50° B．40° C．30° D．25°
3．如图，四边形ABCD内接于⊙O，若∠C＝36°，则∠A的度数为(　　)
A．36° B．56° C．72° D．144°
（第1题）（第2题）（第3题）
4．如图，小华同学设计了一个圆的直径的测量器，标有刻度的尺子OA，OB在O点钉在一起，并使它们保持垂直，当测直径时，把O点靠在圆周上，读得刻度OE=8个单位，OF=6个单位，则圆的直径为(　　)21世纪教育网版权所有
A．12个单位 B．10个单位 C．4个单位 D．15个单位
5．如图，已知点E是圆O上的点，B，C分别是劣弧AD的三等分点，∠BOC＝46°，则∠AED的度数为__________．21cnjy.com
（第4题）（第5题）（第6题）
6．如图，量角器外沿上有A，B两点，它们的读数分别是70°，40°，则∠1的度数为__________．www.21-cn-jy.com
7．如图，点C在⊙O上，将圆心角∠AOB绕点O按逆时针方向旋转到∠A′OB′，旋转角为α(0°＜α＜180°)．若∠AOB=30°，∠BCA′=40°，则∠α=_________°
（第7题） （第8题）（第9题）
8．如图，⊙O是△ABC的外接圆，已知∠B＝60°，则∠CAO的度数是__________．
9．如图，已知AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45°.
(1)求∠EBC的度数；(2)求证：BD=CD.
能力提升
10．如图，以原点O为圆心的圆交x轴于A， B两点，交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB＝20°，则∠OCD＝__________.
（第10题） （第11题）
11．如图，正方形ABCD内接于⊙O，P是劣弧AD上任意一点，则∠ABP＋∠DCP＝__________21教育网
12．如图，点A，D，B，C都在⊙O上，OC⊥AB，∠ADC=30°
(1)求∠BOC的度数；
(2)求证：四边形AOBC是菱形．
13．如图，在△ABC中，∠ACB=90°，D是AB的中点，以DC为直径的⊙O交△ABC的边于G，F，E点．2·1·c·n·j·y
求证：(1)F是BC的中点；
(2)∠A=∠GEF.
参考答案
复习巩固
1．C　2.D　3.D
4．B　连接EF，∵∠EOF＝90°，∴EF是圆的直径．由勾股定理，得EF＝＝10.故选B.
5．69°　∵B，C分别是劣弧AD的三等分点，∠BOC＝46°，
∴∠AOD＝3×46°＝138°.∴∠AED＝∠AOD＝69°.
6．15°　由题意知，∠AOB＝70°－40°＝30°.因此∠1＝∠AOB＝15°.
7．110°　∵∠BCA′＝40°，∴∠BOA′＝2∠BCA′＝80°.
∴∠α＝∠AOB＋∠BOA′＝30°＋80°＝110°.
8．30°　如图，延长AO交⊙O于点D，连接CD，则∠D＝∠B＝60°.∵AD是⊙O的直径，∴∠ACD＝90°.∴∠CAO＝90°－∠D＝30°.www-2-1-cnjy-com
9．(1)解：如图，连接AD.
∵AB为⊙O的直径，∴∠ADB＝90°.∴AD⊥BC.
∵AB＝AC，∴∠BAD＝∠CAD＝22.5°.∴∠EBC＝∠CAD＝22.5°.
(2)证明：∵AB＝AC，AD⊥BC，∴BD＝CD.
能力提升
10．65°　设⊙O交y轴的负半轴于点E，连接AE，则∠OCD＝∠DAE＝∠DAB＋∠BAE.
∵∠EOB＝90°，
∴∠BAE＝∠EOB＝×90°＝45°.
∴∠OCD＝20°＋45°＝65°.
11．45°　连接AO，DO，则∠AOD＝90°，
所以的度数为90°，即与的度数之和为90°.故∠ABP＋∠DCP＝45°.
∵DC是O的直径，∴DF⊥BC.∴BF＝FC，即F是BC的中点．
图①图②
(2)∵D，F分别是AB，BC的中点，∴DF∥AC，∠A＝∠BDF.
∵∠BDF＝∠GEF，∴∠A＝∠GEF.
证法二：(1)如图②，连接DF，DE.∵DC是O的直径，∴∠DEC＝∠DFC＝90°.
∵∠ECF＝90°，∴四边形DECF是矩形．∴EF＝CD，DF＝EC.
∵D是AB的中点，∠ACB＝90°，∴EF＝CD＝BD＝AB.∴Rt△DBF≌Rt△EFC(HL)．
故BF＝FC，即F是BC的中点．
(2)∵△DBF≌△EFC，∴∠BDF＝∠FEC，∠B＝∠EFC.
∵∠ACB＝90°，(也可证AB∥EF，得∠A＝∠FEC)，∴∠A＝∠FEC.
∵∠FEG＝∠BDF，由(1)可知DF∥AC，∴∠A＝∠BDF.∴∠A＝∠GEF.