2.6 正多边形和圆

§2.6正方形与圆
【知识点总结】
正方形的概念
各边相等、各角也相等的多边形叫做正多边形.
例1：下列说法中，正确的是（ ）
平行四边形是正四边形 B.矩形是正四边形 C.菱形是正四边形 D正方形是正四边形
正多边形的画法
利用量角器可以画出任意正多边形；利用直尺和圆规可以作出一些特殊的正多边形.
例2：画出边长为1cm的圆的内接正六边形.
【典例展示】
题型一 对称性问题
例1：一个正多边形中心旋转60°后，才与原正方形第一次重合，那么这个正多边形（ ）
是轴对称图形，但不是中心对称图形 B.是中心对称图形，但不是轴对称图形
C.既是对称图形，也是中心对称图形 D.既不是轴对称图形，也不是中心对称图形
题型二 新定义问题
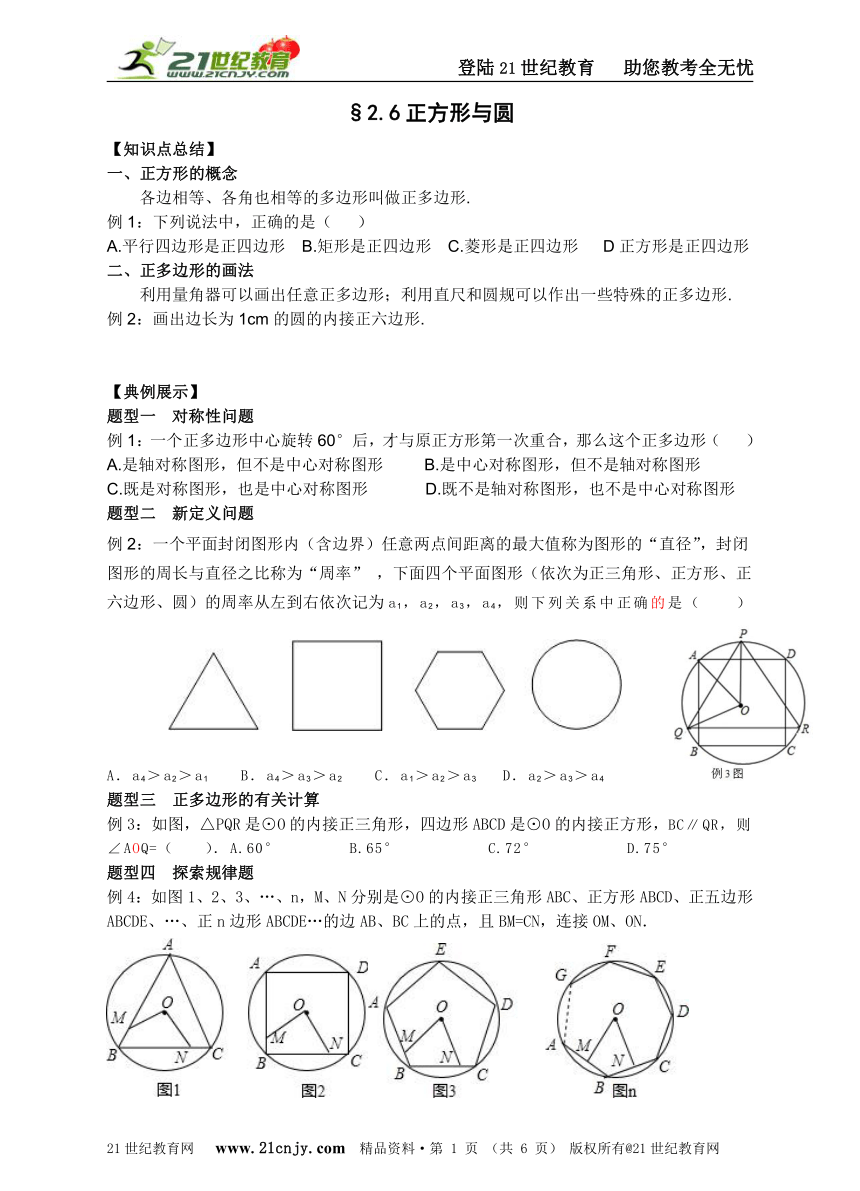
例2：一个平面封闭图形内（含边界）任意两点间距离的最大值称为图形的“直径”，封闭图形的周长与直径之比称为“周率” ，下面四个平面图形（依次为正三角形、正方形、正六边形、圆）的周率从左到右依次记为a1，a2，a3，a4，则下列关系中正确的是（　　）
A．a4＞a2＞a1 B．a4＞a3＞a2 C．a1＞a2＞a3 D．a2＞a3＞a4
题型三 正多边形的有关计算
例3：如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，BC∥QR，则∠AOQ=（ ）．A.60° B.65° C.72° D.75°
题型四 探索规律题
例4：如图1、2、3、…、n，M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点，且BM=CN，连接OM、ON．
（1）求图1中∠MON的度数；
（2）图2中∠MON的度数是 ，图3中∠MON的度数是 ；
（3）试探究∠MON的度数与正n边形边数n的关系（直接写出答案）．
【误区警示】
误点1 对正多边形的概念理解不透彻
例1：判断下列说法是否正确.
各边相等的多边形是正方形
圆内接菱形是正方形
各角相等的圆内接多边形是正方形
误点2 不理解正多边形与圆的关系致错
例2：如图，在⊙O中，OA=AB，OC⊥AB，则下列结论中结论错误的是（ ）
弦AB的长等于园内接正六边形的边长
弦AC的长等于圆内接正十二边形的边长
弧AC=弧BC
D.∠BAC=30°
2.6 正多边形和圆
复习巩固
1．一个边长为2的正多边形的内角和是其外角和的2倍，则这个正多边形的半径是(　　)
A．2 B． C．1 D．
2．半径相等的圆的内接正三角形、正方形、正六边形的边长之比为(　　)
A．1∶∶ B．∶∶1
C．3∶2∶1 D．1∶2∶3
3．如图，在⊙O中，OA＝AB，OC⊥AB，则下列结论错误的是(　　)
A．弦AB的长等于圆内接正六边形的边长
B．弦AC的长等于圆内接正十二边形的边长
C．
D．∠BAC＝30°
4．如图，两个正六边形的边长均为1，其中一个正六边形的一边恰在另一个正六边形的对角线上，则这个图形外轮廓线的周长是(　　)21世纪教育网版权所有
A．7 B．8 C．9 D．10
（第3题）（第4题）
5．一个中心角等于24°的正多边形的边数为__________；一个外角等于24°的正多边形的边数为__________．21cnjy.com
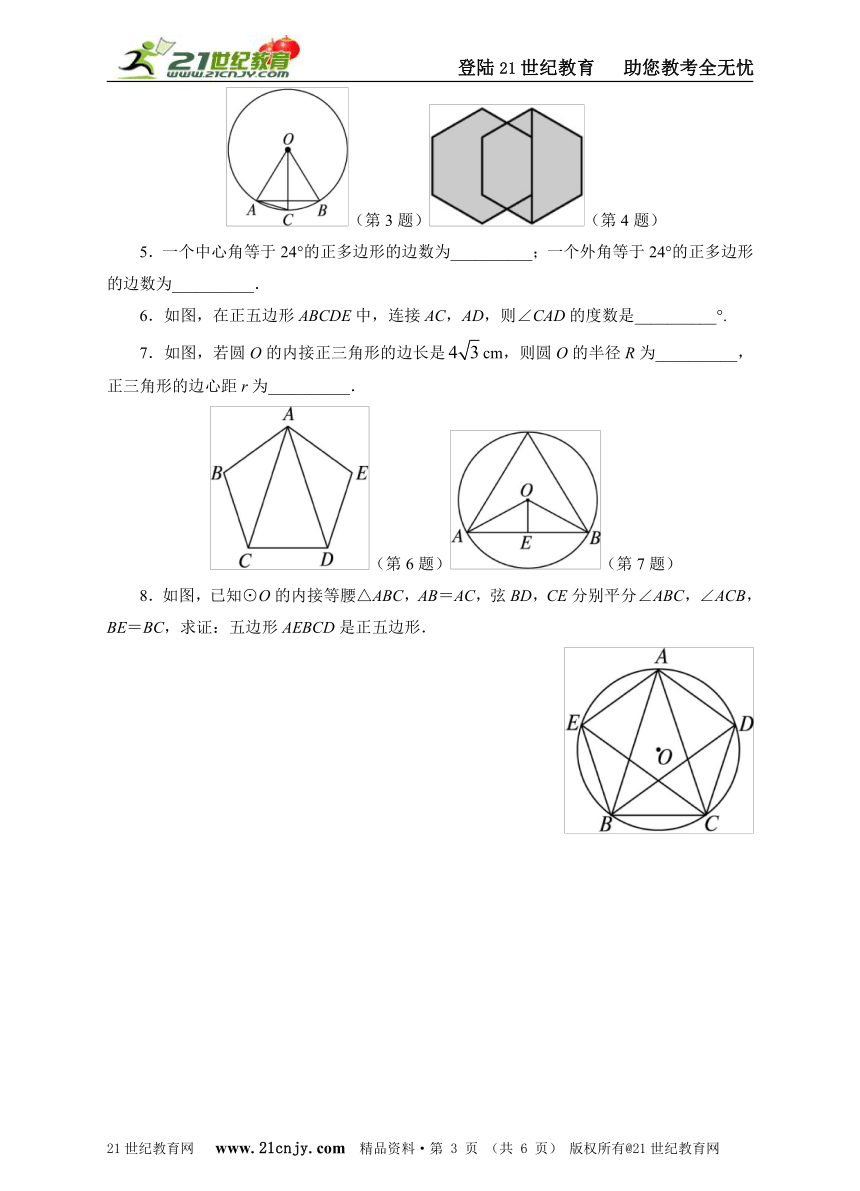
6．如图，在正五边形ABCDE中，连接AC，AD，则∠CAD的度数是__________°.
7．如图，若圆O的内接正三角形的边长是cm，则圆O的半径R为__________，正三角形的边心距r为__________．21·cn·jy·com
（第6题）（第7题）
8．如图，已知⊙O的内接等腰△ABC，AB＝AC，弦BD，CE分别平分∠ABC，∠ACB，BE＝BC，求证：五边形AEBCD是正五边形．www.21-cn-jy.com
能力提升
9．将边长为3cm的正三角形各边三等分，以这六个分点为顶点构成一个正六边形，则这个正六边形的面积为(　　)2·1·c·n·j·y
A．cm2 B．cm2 C．cm2 D．cm2
10．如图，⊙O的内接正多边形周长为3，⊙O的外切正多边形周长为3.4，则下列各数中与此圆的周长最接近的是(　　)【来源：21·世纪·教育·网】
A． B． C． D．
11．如果圆内接正方形的面积为36cm2，那么同圆外切正方形的面积等于__________．
（第10题）（第12题）
12．如图，已知正n边形边长为a，边心距为r，求正n边形的半径R、周长P和面积S.
13．如图，有六个矩形水池环绕．矩形的内侧一边所在直线恰好围成正六边形ABCDEF，正六边形的边长为4 m．要从水源点P处向各水池铺设供水管道，求这些管道的总长度的最短米数．21·世纪*教育网
参考答案
复习巩固
1．A；2．B；3．D；
4．B　由正六边形轴对称的性质可知重叠部分上面的两条线段的长恰为一条边长，故所求外轮廓线的周长是8.www-2-1-cnjy-com
5．15　15
6．36　∵∠BAE＝＝108°，
∴∠CAD＝∠BAE＝36°.
7．4cm　2cm　由题意知AB＝cm，∠AOB＝2∠AOE＝120°，
于是知∠AOE＝60°，∠OAE＝30°.
故AE＝cm，R＝OA＝4cm，r＝OE＝2cm.
8．证明：在△ABC中，
∵AB＝AC，∴∠ABC＝∠ACB.
又∵BD，CE分别平分∠ABC，∠ACB，
∴∠ABD＝∠DBC＝∠ACE＝∠ECB.
∴.
又∵BE＝BC，
∴，即.
∴点A，E，B，C，D把⊙O五等分．
故五边形AEBCD是正五边形．
能力提升
9．A　正六边形的面积等于正三角形的面积减去三个小正三角形的面积．
10．C　由题图知，⊙O的内接正多边形的周长＜⊙O的周长＜⊙O的外切正多边形的周长，即3＜⊙O的周长＜3.4，而3＜＜3.4，故选C21教育网
11．72cm2　如图，AB＝6cm，AO＝cm，PD＝2PA＝2AO＝cm，
故所求外切正方形的面积为72cm2.
12．解：∵OM⊥AB于点M，b 1
∴AM＝BM＝AB＝a.
所以PB＝AB＝4m，BH＝AB＝2m.在Rt△BPH中，利用勾股定理可得PH＝(m)，(m)．2-1-c-n-j-y
因此从水源点P处向各水池铺设供水管道，这些管道的总长度最短是m.