2.7 弧长及扇形的面积

§2.7弧长及扇形的面积
【知识点总结】
弧长公式
圆的周长公式：.其中是圆的周长与直径的比值，称之为圆周率.
弧长公式：.其中n表示1°的圆心角的倍数，它不带单位，R为圆的半径，为n°的圆心角所对的弧长.
例1：如图，AB是⊙O的切线，半径OA=2，OB交⊙O于点C，∠B=30°，则劣弧AC的长是
（结果保留）.
扇形的面积公式
一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.
扇形的面积公式.其中n与弧长公式中的n一样，理解为1°的圆心角的倍数，不带单位，要注意与弧长公式进行比较，避免混淆.与三角形的面积公式相似，可以把扇形看成一个曲边三角形，把弧长看作是底，R看成是高，这样易于记忆.www.21-cn-jy.com
例2：如图，在6×6的方格中（共有36个小正方形），每个小方格都是边长为1的正方形，将线段OA绕点O按逆时针方向旋转得到OB（顶点均在格点上），则阴影部分面积等于 ．　　21*cnjy*com
【典例展示】
题型一 列方程求解题
例1：（1）一个扇形的圆心角是120°，面积为，那么这个扇形的弧长为 cm
已知一个扇形的半径等于一个圆的半径的倍，且面积相等，则这个扇形的圆心角是 度.
题型二 求路径长的问题
例2：已知一个半圆形工件，未搬动前如图所示，直接平行于地面放置，搬动时为了保护圆弧部分不受损伤，现将半圆作如图所示的无滑动翻转，使它的直径紧贴地面，再将它沿地面平移50米，半圆的直径为4米，则圆心O所经过的路线长是 米．
题型三 求阴影部分的面积
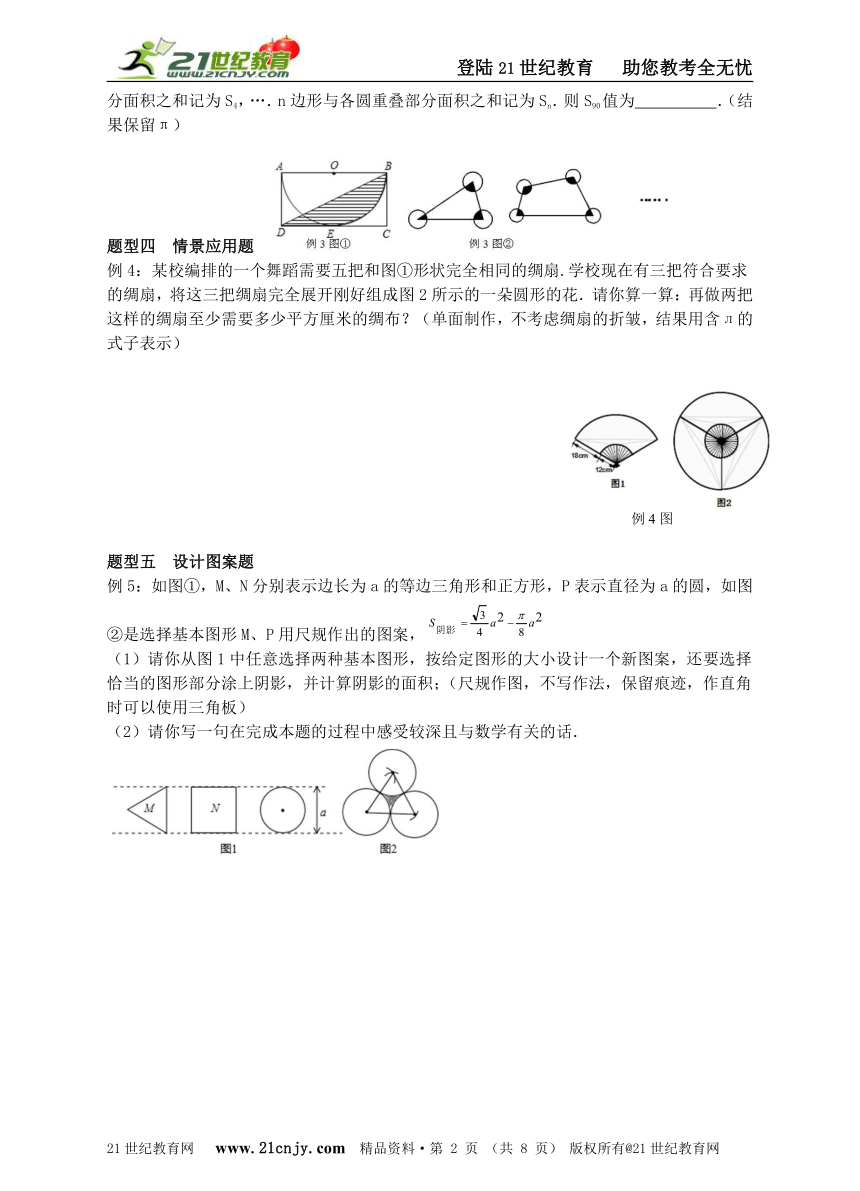
例3：（1）如图①所示，在矩形ABCD中，BC=2,DC=4,以AB为直径的半圆O与DC相切于点E，则阴影部分的面积为 （结果保留）www-2-1-cnjy-com
（1）如图②，一次以三角形、四边形、...、n边形的各顶点为圆心画半径为1的圆，且圆与圆之间两两部相交.把三角形与各圆不重叠部分的面积之和记为S3，四边形与各圆重叠部分面积之和记为S4，…．n边形与各圆重叠部分面积之和记为Sn．则S90值为 ．（结果保留π）2-1-c-n-j-y
题型四 情景应用题
例4：某校编排的一个舞蹈需要五把和图①形状完全相同的绸扇.学校现在有三把符合要求的绸扇，将这三把绸扇完全展开刚好组成图2所示的一朵圆形的花．请你算一算：再做两把这样的绸扇至少需要多少平方厘米的绸布？（单面制作，不考虑绸扇的折皱，结果用含л的式子表示）21cnjy.com
题型五 设计图案题
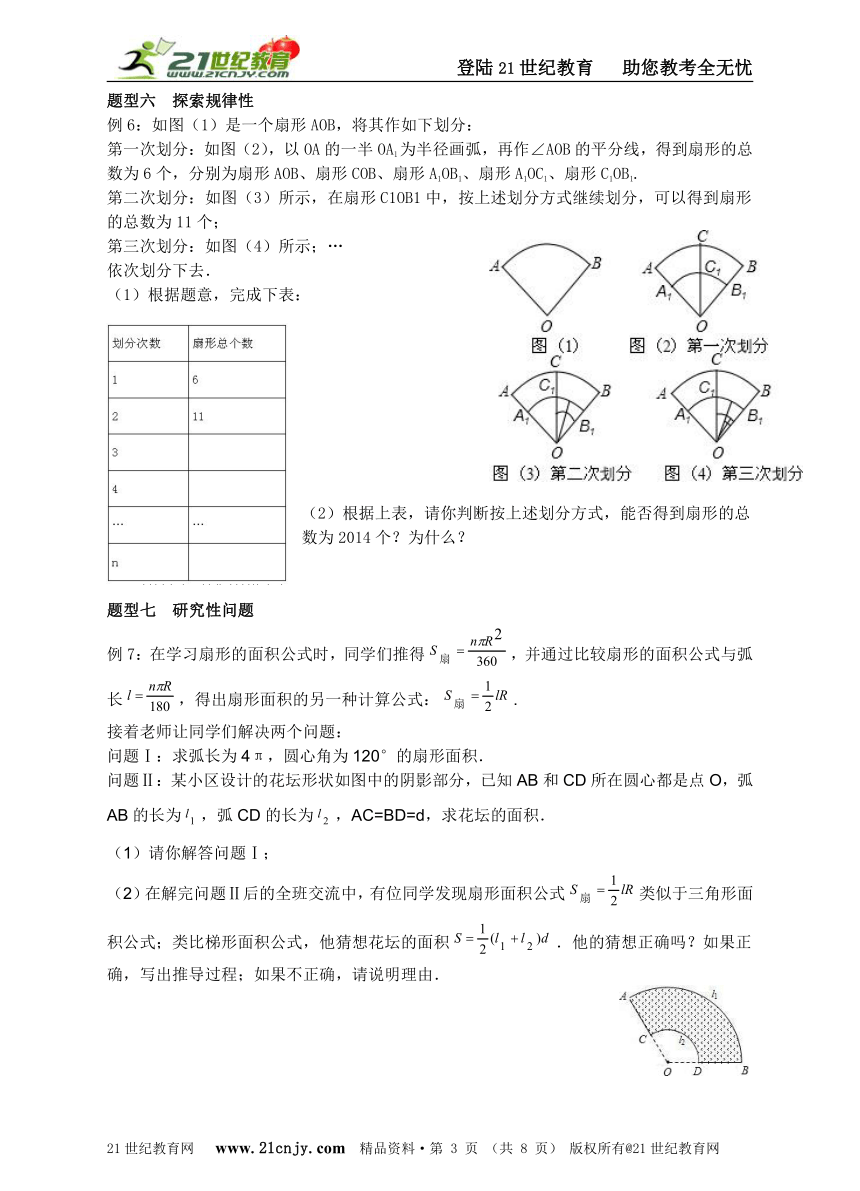
例5：如图①，M、N分别表示边长为a的等边三角形和正方形，P表示直径为a的圆，如图②是选择基本图形M、P用尺规作出的图案，21·cn·jy·com
（1）请你从图1中任意选择两种基本图形，按给定图形的大小设计一个新图案，还要选择恰当的图形部分涂上阴影，并计算阴影的面积；（尺规作图，不写作法，保留痕迹，作直角时可以使用三角板）【来源：21·世纪·教育·网】
（2）请你写一句在完成本题的过程中感受较深且与数学有关的话．
题型六 探索规律性
例6：如图（1）是一个扇形AOB，将其作如下划分：
第一次划分：如图（2），以OA的一半OA1为半径画弧，再作∠AOB的平分线，得到扇形的总数为6个，分别为扇形AOB、扇形COB、扇形A1OB1、扇形A1OC1、扇形C1OB1.
第二次划分：如图（3）所示，在扇形C1OB1中，按上述划分方式继续划分，可以得到扇形的总数为11个；21教育网
第三次划分：如图（4）所示；…
依次划分下去．
（1）根据题意，完成下表：
（2）根据上表，请你判断按上述划分方式，能否得到扇形的总数为2014个？为什么？
题型七 研究性问题
例7：在学习扇形的面积公式时，同学们推得，并通过比较扇形的面积公式与弧长，得出扇形面积的另一种计算公式：.2·1·c·n·j·y
接着老师让同学们解决两个问题：
问题Ⅰ：求弧长为4π，圆心角为120°的扇形面积．
问题Ⅱ：某小区设计的花坛形状如图中的阴影部分，已知AB和CD所在圆心都是点O，弧AB的长为，弧CD的长为，AC=BD=d，求花坛的面积．21·世纪*教育网
（1）请你解答问题Ⅰ；
（2）在解完问题Ⅱ后的全班交流中，有位同学发现扇形面积公式类似于三角形面积公式；类比梯形面积公式，他猜想花坛的面积．他的猜想正确吗？如果正确，写出推导过程；如果不正确，请说明理由． 【来源：21cnj*y.co*m】
【误区警示】
误点1 错将扇形的弧长当周长而致错
例1：已知扇形的圆心角为60°，半径为15cm，则扇形的周长为 cm（结果保留л）.
误点2 混淆弧长计算公式与扇形面积的计算公式
例2：已知扇形的圆心角为120°，所在圆的半径R为20cm，求扇形的面积
2.7 弧长及扇形的面积
复习巩固
1．如图，已知⊙O的半径OA＝6，∠AOB＝90°，则∠AOB所对的弧AB的长为(　　)
A．2π　　　　　B．3π C．6π D．12π
2．如果某钟表的轴心到分针外端点的长为5cm，那么经过40 min，分针外端点转过的弧长是(　　)
A．cm B．cm C．cm D．cm
3．已知圆上一段弧长为5π，它所对的圆心角为100°，则该圆的半径为(　　)
A．6 B．9 C．12 D．18
4．如果一个扇形的弧长等于它的半径，那么此扇形称为“等边扇形”．则半径为2的“等边扇形”的面积为(　　)【出处：21教育名师】
A．π B．1 C．2 D．
5．如图，扇形纸扇完全打开后，外侧两竹条AB，AC夹角为120°，AB的长为30cm，贴纸部分BD的长为20cm，则贴纸部分的面积为(　　)21教育名师原创作品
A．100πcm2 B．πcm2 C．800πcm2 D．πcm2
（第1题）（第5题）（第8题）
6．在半径为的圆中，45°的圆心角所对的弧长等于__________．
7．若一扇形的面积为12π，半径等于6，则它的圆心角等于______．
8．如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则凸轮的周长等于__________.
9．如图，AB是半圆O的直径，AB＝2R，C，D为该半圆的三等分点，求阴影部分的面积．
（第9题）
能力提升
10．如图，有一长为4cm，宽为3cm的长方形木板在桌面上做无滑动的翻滚(顺时针方向)，木板上的顶点A的位置变化为A→A1→A2，其中第二次翻滚被桌面上一小木块挡住，使木板边沿A2C与桌面成30°角，则点A翻滚到A2位置时，共走过的路径长为(　　)
A．10cm B．3.5πcm C．4.5πcm D．2.5πcm
11．如图所示，扇形AOB的圆心角为120°，半径为2，则图中阴影部分的面积为(　　)
A． B． C． D．
（第10题）（第11题）
12．如图，分别以Rt△ABC的三边AB，BC，CA为直径向外作半圆，AB左边阴影部分的面积为S1，右边阴影部分的面积和为S2，则(　　)21*cnjy*com
A．S1＝S2 B．S1＜S2 C．S1＞S2 D．无法确定
（第12题）（第13题）
13．如图，已知菱形ABCD的边长为1.5cm，B，C两点在扇形AEF的上，求的长度及扇形ABC的面积．【版权所有：21教育】
参考答案
复习巩固
1．B；2．B　轴心到分针外端点的长为5cm，即半径R＝5cm，经过40min，分针转过的圆心角的度数为240°，可求得弧长是cm.21世纪教育网版权所有
3．B；4．C；5．D；6．1；7．120°；8．π　∵△ABC为正三角形，∴∠A＝∠B＝∠C＝60°，AB＝AC＝BC＝1.∴.根据题意可知“凸轮”的周长为三个弧长的和，即凸轮的周长.
9．解：∵，∴∠CDA＝∠DAB，即CD∥AB.
∴S△ACD＝S△OCD.∴S阴影＝S扇形OCD＝.
能力提升
10．B　由勾股定理，得AB＝＝5(cm)．
第一次翻滚，点A绕点B转到点A1的位置，转过的圆心角为90°，半径是线段AB的长度；第二次翻滚，点A1绕点C转到点A2的位置，转过的圆心角为90°－30°＝60°，半径是3cm，两次翻滚点A共走过的路径长是两次转过的弧长之和：(cm)．故选B.
11．A　过点O作OD⊥AB，
∵∠AOB＝120°，OA＝2，∴∠OAD＝90°－＝180°－＝30°.
∴OD＝OA＝×2＝1，.∴AB＝2AD＝.
∴S阴影＝S扇形OAB－S△AOB＝.故选A.
12．A　S1＝π·，S2＝π·，