2.8 圆锥的侧面积

§2.8圆锥的侧面积和全面积
【知识点总结】
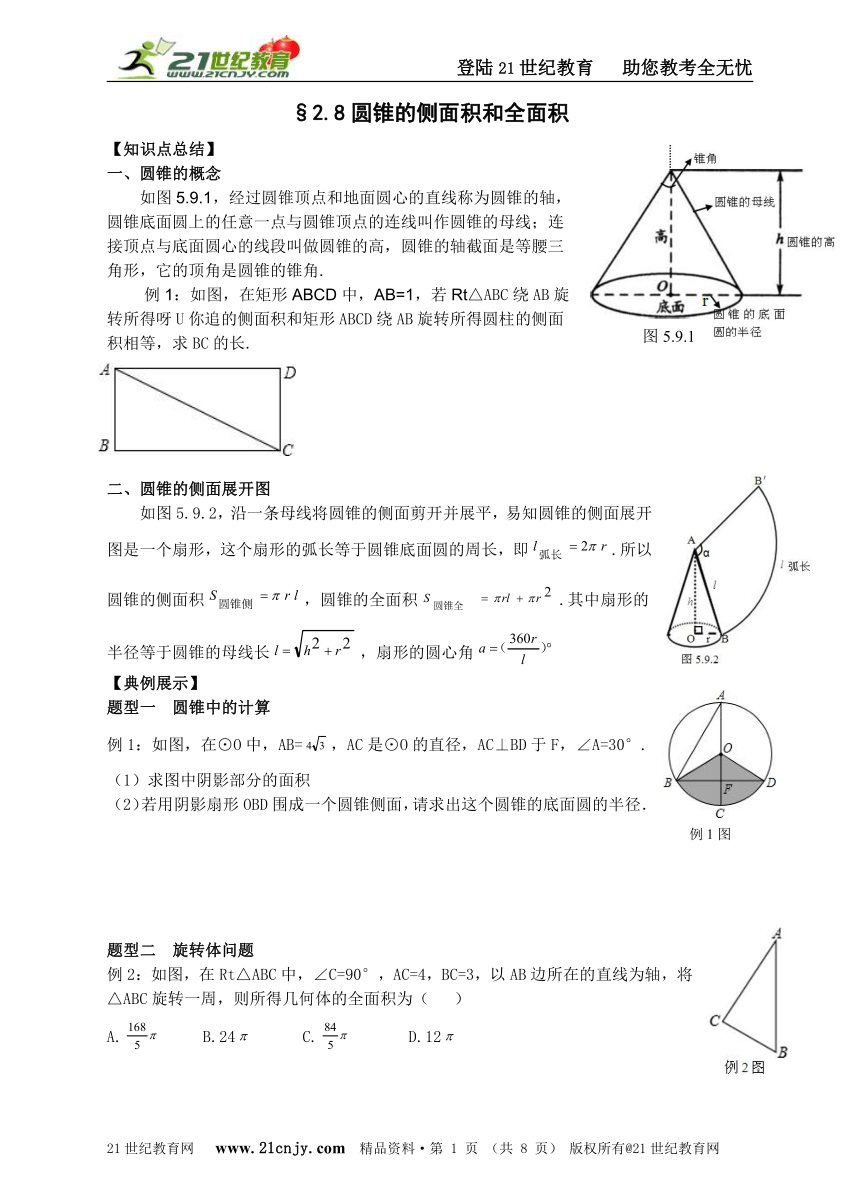
圆锥的概念
如图5.9.1，经过圆锥顶点和地面圆心的直线称为圆锥的轴，圆锥底面圆上的任意一点与圆锥顶点的连线叫作圆锥的母线；连接顶点与底面圆心的线段叫做圆锥的高，圆锥的轴截面是等腰三角形，它的顶角是圆锥的锥角.【出处：21教育名师】
例1：如图，在矩形ABCD中，AB=1，若Rt△ABC绕AB旋转所得呀U你追的侧面积和矩形ABCD绕AB旋转所得圆柱的侧面积相等，求BC的长.【版权所有：21教育】
二、圆锥的侧面展开图
如图5.9.2，沿一条母线将圆锥的侧面剪开并展平，易知圆锥的侧面展开图是一个扇形，这个扇形的弧长等于圆锥底面圆的周长，即.所以圆锥的侧面积，圆锥的全面积.其中扇形的半径等于圆锥的母线长，扇形的圆心角21教育名师原创作品
【典例展示】
题型一 圆锥中的计算
例1：如图，在⊙O中，AB=，AC是⊙O的直径，AC⊥BD于F，∠A=30°.
求图中阴影部分的面积
（2）若用阴影扇形OBD围成一个圆锥侧面，请求出这个圆锥的底面圆的半径．
题型二 旋转体问题
例2：如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，以AB边所在的直线为轴，将△ABC旋转一周，则所得几何体的全面积为（ ）21*cnjy*com
A. B.24 C. D.12
题型三 空间最短问题
例3：如图，圆锥的地面半径为5，母线长为20，已知蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是（ ）【来源：21cnj*y.co*m】
A.8 B. C. D.
题型四 应用题
例4：如图，从一直径为2的圆形铁皮中剪下一个圆心角为90°的扇形.
求这个扇形的面积
（2）在剩下的三块余料中，能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥？请说明理由（3）当⊙O的半径R（R＞0）为任意值时，（2）中的结论是否仍然成立？请说明理由．
【误区警示】
误点1 混淆圆锥的侧面积与全面积的概念
例1：如果圆锥的底面周长为20，侧面展开后所得的扇形的圆心角为120°，则该圆锥的全面积为（ ）21世纪教育网版权所有
A.100 B.200 C.300 D.400
误点2 误将圆锥底面圆的半径当作圆锥侧面展开图（扇形）的半径
例2：已知圆锥的侧面展开图是一个半圆，圆锥的底面积为15cm2,求圆锥的侧面积.
【直击中考】
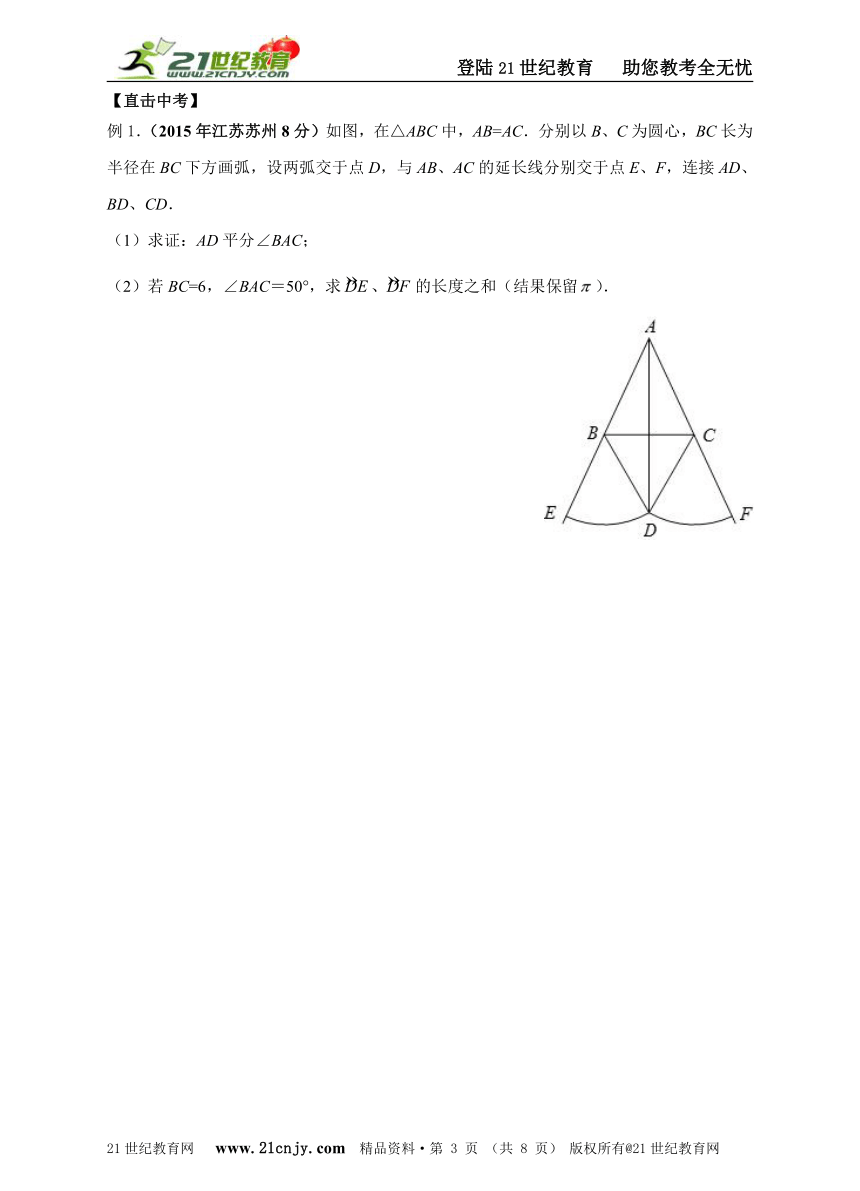
例1．（2015年江苏苏州8分）如图，在△ABC中，AB=AC．分别以B、C为圆心，BC长为半径在BC下方画弧，设两弧交于点D，与AB、AC的延长线分别交于点E、F，连接AD、BD、CD．21教育网
（1）求证：AD平分∠BAC；
（2）若BC=6，∠BAC＝50(，求的长度之和（结果保留）．
2.8 圆锥的侧面积
复习巩固
1．如图，已知一圆锥侧面展开图的扇形面积为65πcm2，扇形的弧长为10πcm，则此圆锥的母线长是(　　)21cnjy.com
A．5cm B．10cm C．12cm D．13cm
2．在综合实践活动课上，小明同学用纸板制作了一个圆锥形漏斗模型．如图所示，它的母线长BC＝10cm，高OC＝8cm，则这个圆锥形漏斗的侧面积是(　　)
A．30cm2 B．30πcm2 C．60πcm2 D．120cm2
（第1题）（第2题）（第3题）
3．如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型．若圆的半径为r，扇形的半径为R，扇形的圆心角等于90°，则r与R之间的关系是(　　)
A．R＝2r B．R＝r C．R＝3r D．R＝4r
4．如图，把一个半径为12cm的圆形硬纸片等分成三个扇形，用其中一个扇形制作成一个圆锥形纸筒的侧面(衔接处无缝隙且不重叠)，则圆锥的底面半径是__________cm.
（第4题）（第5题）（第6题）
5．下面是一圆锥的轴截面图，则此圆锥的侧面展开图的圆心角等于______．
6．一个几何体由圆锥和圆柱组成，其尺寸如图所示，则该几何体的全面积(即表面积)为__________．(结果保留π)21·cn·jy·com
7．如图所示，这是一个由圆柱体材料加工而成的零件，它是以圆柱体的上底面为底面，在其内部“掏取”一个与圆柱体等高的圆锥体而得到的，其底面直径AB＝12cm，高BC＝8cm，求这个零件的表面积．(结果保留根号)www.21-cn-jy.com
能力提升
8．已知点O为一圆锥的顶点，点M为该圆锥底面上一点，点P在母线OM上，一只蚂蚁从P点出发，绕圆锥侧面爬行，回到P点时所爬过的最短路线的痕迹如图所示．若沿母线OM将圆锥侧面剪开展开，则所得侧面展开图是(　　)2·1·c·n·j·y

9．现有30%圆周的一个扇形彩纸片，该扇形的半径为40cm，小红同学为了在“六一”儿童节联欢晚会上表演节目，她打算剪去部分扇形纸片后，利用剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠)，那么剪去的扇形纸片的圆心角为(　　)
A．9° B．18° C．63° D．72°
10．一个圆锥的高为3，侧面展开图是半圆，求：
(1)该圆锥的母线与底面半径之比；
(2)该圆锥的表面积．
11．如图，一个纸杯的母线延长后形成的立体图形是圆锥，该圆锥的侧面展开图是扇形OAB，经测量，纸杯上开口圆的直径是6cm，下底圆直径为4cm，母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积．(面积计算结果用π表示)【来源：21·世纪·教育·网】
（第11题）（第12题）
12. (2015·安庆·一摸)已知,如图，以△ABC的一边BC为直径的⊙O分别交AB、AC于点D、E.下面判断中：①当△ABC为等边三角形时，△ODE是等边三角形；②当△ODE是等边三角形时，△ABC为等边三角形；③当时，△ODE是直角三角形；④当△ODE是直角三角形时，.正确的结论有（ ）21·世纪*教育网
A.1个 B.2个 C.3个 D.4个
参考答案
复习巩固
1．D
2．C　由勾股定理，得OB＝＝6(cm)．
l＝2π×6＝12π
故这个圆锥的侧面积是lr＝×12π×10＝60π(cm2)．
3．D　因为圆形和扇形纸片能围成一个圆锥模型，所以圆的周长等于扇形的弧长，故＝2πr，即R＝4r.故选D.www-2-1-cnjy-com
4．4　半径为12cm圆的三分之一弧长为·2π·12＝8π，它等于圆锥的底面周长，故有＝4(cm)．2-1-c-n-j-y
5．90°　∵2π×3＝，
∴n＝90.
6．68π　圆锥的母线长是＝5.
圆锥的侧面积是×8π×5＝20π，
圆柱的侧面积是8π×4＝32π.
几何体的下底面面积是π×42＝16π.
故所求几何体的全面积(即表面积)为20π＋32π＋16π＝68π.
7．解：这个零件的底面积＝π×＝36π(cm2)，
这个零件的外侧面积＝12π×8＝96π(cm2)，
圆锥母线长OC＝＝10(cm)，
这个零件的内侧面积＝×12π×10＝60π(cm2)，
因此这个零件的表面积为36π＋96π＋60π＝192π(cm2)．
能力提升
8．D
9．B　30%圆周的扇形彩纸片的圆心角为360°×30%＝108°.
设剪去的扇形纸片的圆心角为n°，则2π×10＝，解得n＝18.故选B.
10．解：如图，设圆锥的轴截面为△ABC，过点A作AO⊥BC于点O，设母线长AB＝l，底面O的半径为r，高AO＝h.　　21*cnjy*com
(2)由R＝24，得R－8＝16.
所以S扇形OCD＝×4π×16＝32π(cm2)，
S扇形OAB＝×6π×24＝72π(cm2)．
所以S纸杯侧＝S扇形OAB－S扇形OCD＝72π－32π＝40π(cm2)．
又因为S纸杯底＝＝4π(cm2)，所以S纸杯表＝40π＋4π＝44π(cm2)．
12. 答案： C。