人教版四年级下册乘法分配律 教学设计(表格式)
文档属性
| 名称 | 人教版四年级下册乘法分配律 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 917.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 20:33:51 | ||
图片预览


文档简介
教学设计
课程标题 乘法分配律
内容分析
教学目标 1、通过计算、画图、想象、交流等数学活动,发现并理解乘法分配律。 2、经历探究乘法分配律的活动,发现规律、验证猜想、概括和感悟探究的一般过程,积累推理的经验,感悟模型思想。 3、在学习活动中不断产生对数学的好奇和求知欲,着重培养良好的学习习惯。
教学重点 理解和掌握乘法分配律的意义和应用。
教学难点 乘法分配律的推理及应用。
学情分析
学生具有很好的自主探究、团队合作、与人交流的习惯,在学习了乘法交换律和乘法结合律知识后,掌握了一些算式的规律,有了一些探究规律的方法和经验,只要教师注意指导、指点,就一定会获得很好的教学效果。
过程设计
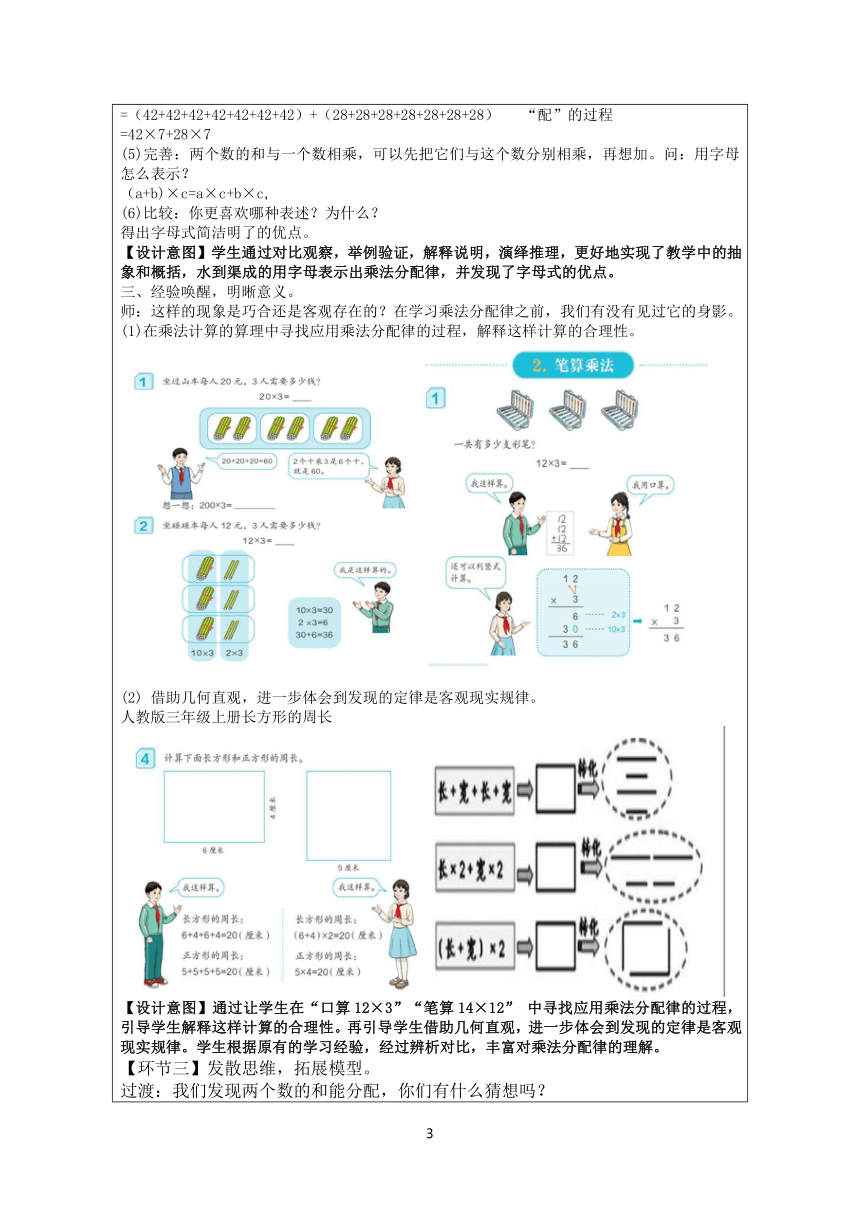
【环节一】看图写式,感知模型 出示图片: (1)仔细观察,从图中你读懂了什么? 完善表述:已经一件上衣45元,一条裤子28元,买这样的7套需要多少钱? (2)你会列式解决吗?跟你的同桌说一说算式的意思。 42×7+28×7=490(元) (42+28)×7=490(元) (3)反馈:结合图说一说算式的意思。 横着看,先算出7件上衣的价钱,再算7条裤子的价钱,最后合起来是一共的价钱。 竖着看,先算出一套衣服的价钱,再算出这样的7套。 (4)观察比较这两条算式,你有什么发现? 得出: (42+28)×7=42×7+28×7 【设计意图】通过实物图片呈现购买服装的生活情境,让学生把抽象的问题具体化,既培养学生读图说图的能力,又在学生列式计算的基础上,引导学生结合情境说算理,加强图与式的联系,从乘法的意义出发,帮助学生初步感知乘法分配律的模型。 【环节二】自主探索,理解模型 出示教材第26页例7 同学们参加植树活动,一共分成25个小组,每组中4人负责挖坑、种树,2人负责抬水、浇树。每组要种5棵树,每棵树要浇2桶水。 (一)请根据自己的理解列出算式。 想一想,还能怎样列式? 4人小组,组内分享想法。 (二)展示学生所列算式,由浅入深反馈,学生自主说一说是怎么想的? 小结:我们还可以从乘法的意义来看,得到下面算式。 (4+2)×25=4×25+2×25 6个25=4个25+2个25 出示面积图: 4cm 2cm 25cm 师:这个图求面积可以怎么列式?这两种算法分别表示什么意思? 小结:同学们真厉害,从不同的角度说明(4+2)×25=4×25+2×25。 【设计意图】在看图写算式的基础上,引导学生逆向思维,通过例题得出两种方法计算结果相同,进一步通过数与形的结合,帮助学生理解算理,发现等式的特点,有效打通乘法分配律与几个几的关系,强化学生对乘法分配律内涵的理解,实现从乘法分配律外在的“形”内化到理解乘法分配律内在的“魂”。 二、举例验证,归纳规律。 (42+28)×7=42×7+28×7 (4+2)×25=4×25+2×25 (1)举例:观察这两个等式,你一定发现了什么规律,你能试着写一写像这样的等式吗? (2)想象:写完之后想一想,如果画出相应的图是什么样的,左右两边的式子分别表示什么意思呢?(用你喜欢的方法验证) (3)思考:观察这些等式,你有什么发现?用自己的话说一说你发现的运算规律。 发现:括号里的每个数分别和括号外的数相乘,再把他们的积想加。这就是乘法分配律。 (4)质疑:为什么叫分配律呢?分配了什么? 预设1:把括号内的数字分别跟括号外的数字相乘,就是分配。 预设2:把括号外的数字分配给括号内的每个数字。 预设3: (42+28)×7 =(42+28)+(42+28)+(42+28)+(42+28)+(42+28)+(42+28)+(42+28) =42+28+42+28+42+28+42+28+42+28+42+28+42+28 “分”的过程 =(42+42+42+42+42+42+42)+(28+28+28+28+28+28+28) “配”的过程 =42×7+28×7 (5)完善:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再想加。问:用字母怎么表示? (a+b)×c=a×c+b×c, (6)比较:你更喜欢哪种表述?为什么? 得出字母式简洁明了的优点。 【设计意图】学生通过对比观察,举例验证,解释说明,演绎推理,更好地实现了教学中的抽象和概括,水到渠成的用字母表示出乘法分配律,并发现了字母式的优点。 三、经验唤醒,明晰意义。 师:这样的现象是巧合还是客观存在的?在学习乘法分配律之前,我们有没有见过它的身影。 (1)在乘法计算的算理中寻找应用乘法分配律的过程,解释这样计算的合理性。 借助几何直观,进一步体会到发现的定律是客观现实规律。 人教版三年级上册长方形的周长 【设计意图】通过让学生在“口算12×3”“笔算14×12” 中寻找应用乘法分配律的过程,引导学生解释这样计算的合理性。再引导学生借助几何直观,进一步体会到发现的定律是客观现实规律。学生根据原有的学习经验,经过辨析对比,丰富对乘法分配律的理解。 【环节三】发散思维,拓展模型。 过渡:我们发现两个数的和能分配,你们有什么猜想吗? 猜想一:两个数的差能分配吗? 猜想二:必须是两个数的和吗?三个数的和可以分配吗? 1.你打算验证你的猜想呢? 学生活动,选择一个猜想进行验证。 有困难的学生提供学习提示: ①猜一猜,减法(或三个数的和)能分配吗? ②举2个例子写下来。 ③闭眼想象,左边表示什么?画图长什么样?右边呢? ④用字母表达你的发现。 2.全班反馈,谁来分享一下自己的想法? 概括小结: 【设计意图】通过猜想、想象、举例的方式,将抽象的算式与具体实物进行对应,归纳概括出乘法分配律的一般运算规律,提升学生的学习能力。让学生把乘法分配律的模型进行拓展,不仅知其然,更知其所以然。 【环节四】练习巩固,应用模型 1.下面哪些算式是正确的?正确的画“√”,错误的画“×”。 56×(19+28)=56×19+28 ( ) 32×(7×3)= 32×7+32×3 ( ) 64×64+36×64= (64+36)× 64 ( ) 思考:如果要算结果,你打算算哪条算式呢?为什么? 2.比一比:你认为哪两个算式的结果相等,为什么? 想一想:乘法结合律和乘法分配律有什么不同? ①形式不一样 ②乘法结合律是同级运算,乘法分配律是两级运算。 3.填一填,算一算:填上一个数使得计算简便并计算。 【设计意图】通过有层次的练习,帮助学生巩固和内化新知。第1题是基础练习,是乘法分配律形的简单回顾。第2题是为了更好地理解乘法分配律,有必要让学生对原有的运算定律进行沟通与比较。乘法结合律和乘法分配律非常相似,学生容易混淆,是学生学习中的易错点,通过对比鉴定,帮助学生感知两者结构的不同。第3题打破学生的思维定势,让学生从理解的角度填数并能简便计算。 【环节五】课堂回顾,积累经验 师:静静地回顾这节课,你有什么收获?我们是怎样一步步学习的?还有什么疑问吗? 【设计意图】梳理学习的基本过程,积累概念学习的基本经验。 (四)板书设计: 乘法分配律 观察 (42+28)×7=42×7+28×7 发现 (4+2)×25=4×25+2×25 举例 想象 验证
评价设计
课堂提问中利用课件对学生进行表扬,开设闯关游戏进行对乘法分配律层次性的探究。 作业设计利用课件一步一步出示,最后展示作业结果。
测试题学生完成后,利用作业小程序反馈到学生每一个人中,让学生能够及时收到自己对本节课的掌握情况和不足处。
教学反思
《乘法分配律》是人教版数学四年级下册的教学内容,与乘法交换律、结合律单一运算相比,乘法分配律含有乘法和加法两种运算,其思维含量更高,学生理解掌握乘法分配律存在一定的困难,作业错误率也很高。如何突破重难点,帮助学生建立对乘法分配律的深刻理解?教学中,我试着从以下几方面进行思考与实践: 1.依托情境,激活内需,初识模型。 课的开始,我借助图示直观,以买衣服的生活情境,引发学生用不同的方式解决问题,唤起学生已有的知识经验。把抽象的问题具体化,既培养学生读图说图的能力,又在学生列式计算的基础上,引导学生结合情境说算理,加强图与式的联系,从乘法的意义出发,帮助学生初步感知乘法分配律的模型,为学生进一步感知乘法分配律的本质意义奠定基础。 2.创设联结,以形促数,理解模型。 在以往的教学中,在得到两个相等的算式后,接下来会延续教学乘法交换律、乘法结合律的方式来组织教学,先让学生提出猜想,再举例、计算、比较得数,由此验证猜想,得出乘法分配律。这样教学得到的乘法分配律没有持久生长的“根”。教学时应立足于算理的理解,创设联结,借助“形象”理解“抽象”,借助“直观”理解“数理”,让学生既知乘法分配律外在的形,更理解其内在的理,推动学生对乘法分配律的内在本质理解。在看图写算式的基础上,我引导学生逆向思维,看算式画图,在学生充分的活动中汇报两种计算方法、出示面积图,进一步通过数与形的结合,帮助学生理解算理,发现等式的特点,有效打通乘法分配律与几个几的关系,强化学生对乘法分配律内涵的理解,实现从乘法分配律外在的“形”内化到理解乘法分配律内在的“魂”。
1
课程标题 乘法分配律
内容分析
教学目标 1、通过计算、画图、想象、交流等数学活动,发现并理解乘法分配律。 2、经历探究乘法分配律的活动,发现规律、验证猜想、概括和感悟探究的一般过程,积累推理的经验,感悟模型思想。 3、在学习活动中不断产生对数学的好奇和求知欲,着重培养良好的学习习惯。
教学重点 理解和掌握乘法分配律的意义和应用。
教学难点 乘法分配律的推理及应用。
学情分析
学生具有很好的自主探究、团队合作、与人交流的习惯,在学习了乘法交换律和乘法结合律知识后,掌握了一些算式的规律,有了一些探究规律的方法和经验,只要教师注意指导、指点,就一定会获得很好的教学效果。
过程设计
【环节一】看图写式,感知模型 出示图片: (1)仔细观察,从图中你读懂了什么? 完善表述:已经一件上衣45元,一条裤子28元,买这样的7套需要多少钱? (2)你会列式解决吗?跟你的同桌说一说算式的意思。 42×7+28×7=490(元) (42+28)×7=490(元) (3)反馈:结合图说一说算式的意思。 横着看,先算出7件上衣的价钱,再算7条裤子的价钱,最后合起来是一共的价钱。 竖着看,先算出一套衣服的价钱,再算出这样的7套。 (4)观察比较这两条算式,你有什么发现? 得出: (42+28)×7=42×7+28×7 【设计意图】通过实物图片呈现购买服装的生活情境,让学生把抽象的问题具体化,既培养学生读图说图的能力,又在学生列式计算的基础上,引导学生结合情境说算理,加强图与式的联系,从乘法的意义出发,帮助学生初步感知乘法分配律的模型。 【环节二】自主探索,理解模型 出示教材第26页例7 同学们参加植树活动,一共分成25个小组,每组中4人负责挖坑、种树,2人负责抬水、浇树。每组要种5棵树,每棵树要浇2桶水。 (一)请根据自己的理解列出算式。 想一想,还能怎样列式? 4人小组,组内分享想法。 (二)展示学生所列算式,由浅入深反馈,学生自主说一说是怎么想的? 小结:我们还可以从乘法的意义来看,得到下面算式。 (4+2)×25=4×25+2×25 6个25=4个25+2个25 出示面积图: 4cm 2cm 25cm 师:这个图求面积可以怎么列式?这两种算法分别表示什么意思? 小结:同学们真厉害,从不同的角度说明(4+2)×25=4×25+2×25。 【设计意图】在看图写算式的基础上,引导学生逆向思维,通过例题得出两种方法计算结果相同,进一步通过数与形的结合,帮助学生理解算理,发现等式的特点,有效打通乘法分配律与几个几的关系,强化学生对乘法分配律内涵的理解,实现从乘法分配律外在的“形”内化到理解乘法分配律内在的“魂”。 二、举例验证,归纳规律。 (42+28)×7=42×7+28×7 (4+2)×25=4×25+2×25 (1)举例:观察这两个等式,你一定发现了什么规律,你能试着写一写像这样的等式吗? (2)想象:写完之后想一想,如果画出相应的图是什么样的,左右两边的式子分别表示什么意思呢?(用你喜欢的方法验证) (3)思考:观察这些等式,你有什么发现?用自己的话说一说你发现的运算规律。 发现:括号里的每个数分别和括号外的数相乘,再把他们的积想加。这就是乘法分配律。 (4)质疑:为什么叫分配律呢?分配了什么? 预设1:把括号内的数字分别跟括号外的数字相乘,就是分配。 预设2:把括号外的数字分配给括号内的每个数字。 预设3: (42+28)×7 =(42+28)+(42+28)+(42+28)+(42+28)+(42+28)+(42+28)+(42+28) =42+28+42+28+42+28+42+28+42+28+42+28+42+28 “分”的过程 =(42+42+42+42+42+42+42)+(28+28+28+28+28+28+28) “配”的过程 =42×7+28×7 (5)完善:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再想加。问:用字母怎么表示? (a+b)×c=a×c+b×c, (6)比较:你更喜欢哪种表述?为什么? 得出字母式简洁明了的优点。 【设计意图】学生通过对比观察,举例验证,解释说明,演绎推理,更好地实现了教学中的抽象和概括,水到渠成的用字母表示出乘法分配律,并发现了字母式的优点。 三、经验唤醒,明晰意义。 师:这样的现象是巧合还是客观存在的?在学习乘法分配律之前,我们有没有见过它的身影。 (1)在乘法计算的算理中寻找应用乘法分配律的过程,解释这样计算的合理性。 借助几何直观,进一步体会到发现的定律是客观现实规律。 人教版三年级上册长方形的周长 【设计意图】通过让学生在“口算12×3”“笔算14×12” 中寻找应用乘法分配律的过程,引导学生解释这样计算的合理性。再引导学生借助几何直观,进一步体会到发现的定律是客观现实规律。学生根据原有的学习经验,经过辨析对比,丰富对乘法分配律的理解。 【环节三】发散思维,拓展模型。 过渡:我们发现两个数的和能分配,你们有什么猜想吗? 猜想一:两个数的差能分配吗? 猜想二:必须是两个数的和吗?三个数的和可以分配吗? 1.你打算验证你的猜想呢? 学生活动,选择一个猜想进行验证。 有困难的学生提供学习提示: ①猜一猜,减法(或三个数的和)能分配吗? ②举2个例子写下来。 ③闭眼想象,左边表示什么?画图长什么样?右边呢? ④用字母表达你的发现。 2.全班反馈,谁来分享一下自己的想法? 概括小结: 【设计意图】通过猜想、想象、举例的方式,将抽象的算式与具体实物进行对应,归纳概括出乘法分配律的一般运算规律,提升学生的学习能力。让学生把乘法分配律的模型进行拓展,不仅知其然,更知其所以然。 【环节四】练习巩固,应用模型 1.下面哪些算式是正确的?正确的画“√”,错误的画“×”。 56×(19+28)=56×19+28 ( ) 32×(7×3)= 32×7+32×3 ( ) 64×64+36×64= (64+36)× 64 ( ) 思考:如果要算结果,你打算算哪条算式呢?为什么? 2.比一比:你认为哪两个算式的结果相等,为什么? 想一想:乘法结合律和乘法分配律有什么不同? ①形式不一样 ②乘法结合律是同级运算,乘法分配律是两级运算。 3.填一填,算一算:填上一个数使得计算简便并计算。 【设计意图】通过有层次的练习,帮助学生巩固和内化新知。第1题是基础练习,是乘法分配律形的简单回顾。第2题是为了更好地理解乘法分配律,有必要让学生对原有的运算定律进行沟通与比较。乘法结合律和乘法分配律非常相似,学生容易混淆,是学生学习中的易错点,通过对比鉴定,帮助学生感知两者结构的不同。第3题打破学生的思维定势,让学生从理解的角度填数并能简便计算。 【环节五】课堂回顾,积累经验 师:静静地回顾这节课,你有什么收获?我们是怎样一步步学习的?还有什么疑问吗? 【设计意图】梳理学习的基本过程,积累概念学习的基本经验。 (四)板书设计: 乘法分配律 观察 (42+28)×7=42×7+28×7 发现 (4+2)×25=4×25+2×25 举例 想象 验证
评价设计
课堂提问中利用课件对学生进行表扬,开设闯关游戏进行对乘法分配律层次性的探究。 作业设计利用课件一步一步出示,最后展示作业结果。
测试题学生完成后,利用作业小程序反馈到学生每一个人中,让学生能够及时收到自己对本节课的掌握情况和不足处。
教学反思
《乘法分配律》是人教版数学四年级下册的教学内容,与乘法交换律、结合律单一运算相比,乘法分配律含有乘法和加法两种运算,其思维含量更高,学生理解掌握乘法分配律存在一定的困难,作业错误率也很高。如何突破重难点,帮助学生建立对乘法分配律的深刻理解?教学中,我试着从以下几方面进行思考与实践: 1.依托情境,激活内需,初识模型。 课的开始,我借助图示直观,以买衣服的生活情境,引发学生用不同的方式解决问题,唤起学生已有的知识经验。把抽象的问题具体化,既培养学生读图说图的能力,又在学生列式计算的基础上,引导学生结合情境说算理,加强图与式的联系,从乘法的意义出发,帮助学生初步感知乘法分配律的模型,为学生进一步感知乘法分配律的本质意义奠定基础。 2.创设联结,以形促数,理解模型。 在以往的教学中,在得到两个相等的算式后,接下来会延续教学乘法交换律、乘法结合律的方式来组织教学,先让学生提出猜想,再举例、计算、比较得数,由此验证猜想,得出乘法分配律。这样教学得到的乘法分配律没有持久生长的“根”。教学时应立足于算理的理解,创设联结,借助“形象”理解“抽象”,借助“直观”理解“数理”,让学生既知乘法分配律外在的形,更理解其内在的理,推动学生对乘法分配律的内在本质理解。在看图写算式的基础上,我引导学生逆向思维,看算式画图,在学生充分的活动中汇报两种计算方法、出示面积图,进一步通过数与形的结合,帮助学生理解算理,发现等式的特点,有效打通乘法分配律与几个几的关系,强化学生对乘法分配律内涵的理解,实现从乘法分配律外在的“形”内化到理解乘法分配律内在的“魂”。
1
