数学人教A版(2019)选择性必修第三册7.1.1条件概率 课件(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册7.1.1条件概率 课件(共25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 328.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-29 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
7.1.1条件概率
1.概率加法公式:
注:
1.事件A与B至少有一个发生的事件叫做A与B的
和事件,记为 (或 );
3.若 为不可能事件,则说事件A与B互斥.
复习引入:
2.事件A与B都发生的事件叫做A与B的积事件,记为 (或 );
2.概率乘法公式:
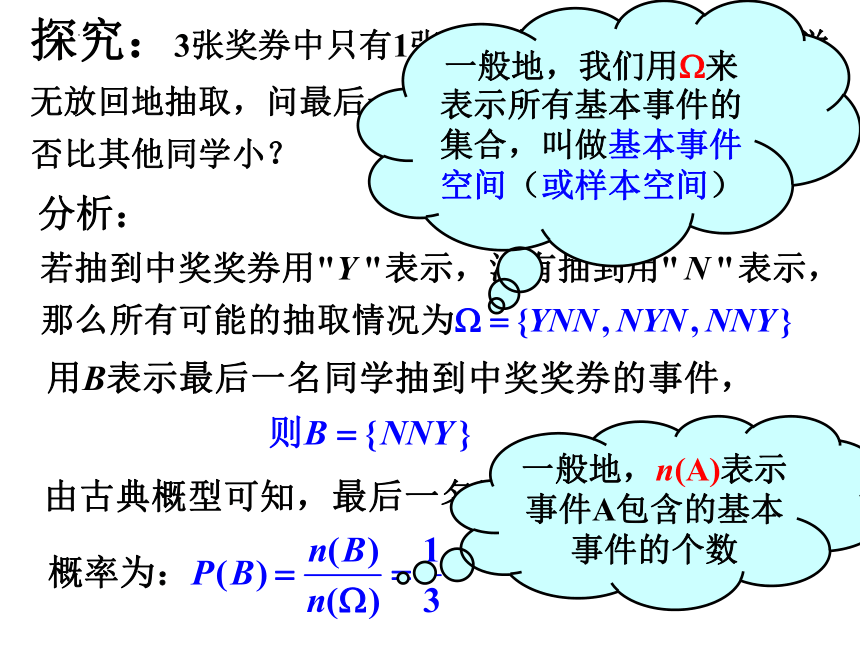
探究:3张奖券中只有1张能中奖,现分别由3名同学
无放回地抽取,问最后一名同学抽到中奖奖券的概率是
否比其他同学小?
分析:
一般地,我们用W来表示所有基本事件的集合,叫做基本事件空间(或样本空间)
一般地,n(A)表示
事件A包含的基本
事件的个数
思考:如果已经知道第一名同学没有抽到中奖奖券,
那么最后一名抽到中奖奖券的概率又是多少?
分析:
不妨设“第一名同学没有抽到中奖奖券”为事件A,
注:P(B|A)表示在事件A发生的条件下B发生的概率
你知道第一名同学的抽奖结果为什么会影响最后一名同学的抽奖结果吗?
分析:
若不知道第一名同学的抽奖结果,则样本空间为
若知道了第一名同学的抽奖结果,则样本空间变成
但因为最后一名中奖的情况只有一种{NNY}
故概率会发生变化
思考:你知道第一名同学的抽奖结果为什么会影响
最后一名同学的抽奖结果吗?
因为已经知道事件A必然发生,所以只需在A发生
的范围内考虑问题,即现在的样本空间为A。
因为在事件A发生的情况下事件B发生,等价于事
件A和事件B同时发生,即AB发生。
故其条件概率为
为了把条件概率推广到一般情形,不妨记原来的
样本空间为W,则有
P(B|A)表示在事件A发生的条件下B发生的概率
(通常适用古典概率模型)
(适用于一般的概率模型)
一般地,设A,B为两个事件,且P(A)>0,则
称为在事件A发生的条件下,事件B发生的条件概率。
一般把P(B|A)读作A发生的条件下B的概率。
注意:
(1)条件概率的取值在0和1之间,即0≤P(B|A) ≤1
(2)如果B和C是互斥事件,则
P(B∪C |A)= P(B|A)+ P(C|A)
(3)要注意P(B|A)与P(AB)的区别,这是分清条件概率
与一般概率问题的关键。
条件概率的定义:
在原样本空间的概率
概率 P(B|A)与P(AB)的区别与联系
联系:事件A,B都发生了
区别:
由条件概率的定义
即 若P(B)>0, 则 P(AB)= P(B)P(A|B) (1)
而 P(AB)= P(BA)
若已知P(B), P(A|B)时, 可以反求P(AB).
对调A、B的位置,则有
故 P(B)P(A|B)=P(A)P(B|A)
(1)和(2)式统称为乘法公式 , 利用
它可计算两个事件同时发生的概率
二、 乘法公式
即 若P(A)>0, 则 P(BA)= P(A)P(B|A) (2)
条件概率计算中注意的问题
1、条件概率的判断:
(1)当题目中出现“在……前提(条件)下”等字眼,一般为条件概率。
(2)当已知事件的发生影响所求事件的概率,一般也认为是条件概率。
2、相应事件的判断:
首先用相应的字母A、B表示出相应的事件,然后分析清楚在哪个事件发生的条件下求哪个事件的概率。
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
解:设第1次抽到理科题为事件A,第2次抽到理科题
为事件B,则第1次和第2次都抽到理科题为事件AB.
(1)从5道题中不放回地依次抽取2道的事件数为
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
解:设第1次抽到理科题为事件A,第2次抽到理科题
为事件B,则第1次和第2次都抽到理科题为事件AB.
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
(3)在第一次抽到理科题的条件下,第二次抽到理科题
的概率。
(3)解法一:由(1)(2)可得,在第一次抽到理科题
的条件下,第二次抽到理科题的概率为
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
(3)在第一次抽到理科题的条件下,第二次抽到理科题
的概率。
解法二:
解法三:
(缩小样本空间)
反思
求解条件概率的一般步骤:
(1)用字母表示有关事件
(2)求P(AB),P(A)或n(AB),n(A)
( 3 )利用条件概率公式求
练习1:甲乙两地都位于长江下游,根据一百多年的气象
记录,知道甲乙两地一年中雨天所占的比例分别为20%
和18%,两地同时下雨的比例为12%,问:
(1)乙地为雨天时甲地也为雨天的概率是多少?
(2)甲地为雨天时乙地也为雨天的概率是多少?
解:设A={甲地为雨天}, B={乙地为雨天},
则P(A)=20%,P(B)=18%,P(AB)=12%,
练习1:甲乙两地都位于长江下游,根据一百多年的气象
记录,知道甲乙两地一年中雨天所占的比例分别为20%
和18%,两地同时下雨的比例为12%,问:
(3)甲乙两市至少一市下雨的概率是多少?
∵{甲乙两市至少一市下雨}=A∪B
而P(A∪B)=P(A)+P(B)-P(AB)
=20%+18%-12%
=26%
∴甲乙两市至少一市下雨的概率为26%
解:设A={甲地为雨天}, B={乙地为雨天},
则P(A)=20%,P(B)=18%,P(AB)=12%,
练一练
2.某种动物出生之后活到20岁的概率为0.7,活到25岁的概率为0.56,求现年为20岁的这种动物活到25岁的概率。
解 设A表示“活到20岁”(即≥20),B表示“活到25岁” (即≥25)
则
所求概率为
0.56
0.7
5
在某次外交谈判中,中外双方都为了自身的利益
而互不相让,这时对方有个外交官提议以抛掷一
颗骰子决定,若已知出现点数不超过3的条件下再
出现点数为奇数则按对方的决议处理,否则按中
方的决议处理,假如你在现场,你会如何抉择?
只需求事件 A 发生的条件下,
事件 B 的概率即P(B|A)
5
2
1
3
4,6
解法一(缩小样本空间法)
3.
解1:
在某次外交谈判中,中外双方都为了自身的利益
而互不相让,这时对方有个外交官提议以抛掷一
颗骰子决定,若已知出现点数不超过3的条件下再
出现点数为奇数则按对方的决议处理,否则按中
方的决议处理,假如你在现场,你会如何抉择?
只需求事件 A 发生的条件下,
事件 B 的概率即P(B|A)
5
2
1
3
4,6
3.
解2:
由条件概率定义得:
解法二(条件概率定义法)
解
4、一个盒子中有6只白球、4只黑球,从中不放回地每次任取1只,连取2次,求 (1) 第一次取得白球的概率; (2) 第一、第二次都取得白球的概率; (3) 第一次取得黑球而第二次取得白球的概率.
设A表示第一次取得白球, B表示第二次取得白球, 则
(2)
(3)
(1)
5.甲,乙,丙3人参加面试抽签,每人的试题通过不放回抽签的方式确定。假设被抽的10个试题签中有4个是难题签,按甲先,乙次,丙最后的次序抽签。试求1)甲抽到难题签,2)甲和乙都抽到难题签,3)甲没抽到难题签而乙抽到难题签,4)甲,乙,丙都抽到难题签的概率。
解 设A,B,C分别表示“甲、乙、丙抽到难签”
则
1. 条件概率的定义.
2. 条件概率的性质.
3. 条件概率的计算方法.
一、基本知识
二、思想方法
1.由特殊到一般
2.类比、归纳、推理
(1)有界性(2)可加性
(古典概型)
(一般概型)
3.数形结合
4. 求解条件概率的一般步骤
用字母表示有关事件
求相关量
代入公式求P(B|A)
课堂小结
送给同学们一段话:
在概率的世界里充满着和我们直觉截然不同的事物。面对表象同学们要坚持实事求是的态度、锲而不舍的精神。尽管我们的学习生活充满艰辛,但我相信只要同学们不断进取、挑战自我,我们一定会达到成功的彼岸!
7.1.1条件概率
1.概率加法公式:
注:
1.事件A与B至少有一个发生的事件叫做A与B的
和事件,记为 (或 );
3.若 为不可能事件,则说事件A与B互斥.
复习引入:
2.事件A与B都发生的事件叫做A与B的积事件,记为 (或 );
2.概率乘法公式:
探究:3张奖券中只有1张能中奖,现分别由3名同学
无放回地抽取,问最后一名同学抽到中奖奖券的概率是
否比其他同学小?
分析:
一般地,我们用W来表示所有基本事件的集合,叫做基本事件空间(或样本空间)
一般地,n(A)表示
事件A包含的基本
事件的个数
思考:如果已经知道第一名同学没有抽到中奖奖券,
那么最后一名抽到中奖奖券的概率又是多少?
分析:
不妨设“第一名同学没有抽到中奖奖券”为事件A,
注:P(B|A)表示在事件A发生的条件下B发生的概率
你知道第一名同学的抽奖结果为什么会影响最后一名同学的抽奖结果吗?
分析:
若不知道第一名同学的抽奖结果,则样本空间为
若知道了第一名同学的抽奖结果,则样本空间变成
但因为最后一名中奖的情况只有一种{NNY}
故概率会发生变化
思考:你知道第一名同学的抽奖结果为什么会影响
最后一名同学的抽奖结果吗?
因为已经知道事件A必然发生,所以只需在A发生
的范围内考虑问题,即现在的样本空间为A。
因为在事件A发生的情况下事件B发生,等价于事
件A和事件B同时发生,即AB发生。
故其条件概率为
为了把条件概率推广到一般情形,不妨记原来的
样本空间为W,则有
P(B|A)表示在事件A发生的条件下B发生的概率
(通常适用古典概率模型)
(适用于一般的概率模型)
一般地,设A,B为两个事件,且P(A)>0,则
称为在事件A发生的条件下,事件B发生的条件概率。
一般把P(B|A)读作A发生的条件下B的概率。
注意:
(1)条件概率的取值在0和1之间,即0≤P(B|A) ≤1
(2)如果B和C是互斥事件,则
P(B∪C |A)= P(B|A)+ P(C|A)
(3)要注意P(B|A)与P(AB)的区别,这是分清条件概率
与一般概率问题的关键。
条件概率的定义:
在原样本空间的概率
概率 P(B|A)与P(AB)的区别与联系
联系:事件A,B都发生了
区别:
由条件概率的定义
即 若P(B)>0, 则 P(AB)= P(B)P(A|B) (1)
而 P(AB)= P(BA)
若已知P(B), P(A|B)时, 可以反求P(AB).
对调A、B的位置,则有
故 P(B)P(A|B)=P(A)P(B|A)
(1)和(2)式统称为乘法公式 , 利用
它可计算两个事件同时发生的概率
二、 乘法公式
即 若P(A)>0, 则 P(BA)= P(A)P(B|A) (2)
条件概率计算中注意的问题
1、条件概率的判断:
(1)当题目中出现“在……前提(条件)下”等字眼,一般为条件概率。
(2)当已知事件的发生影响所求事件的概率,一般也认为是条件概率。
2、相应事件的判断:
首先用相应的字母A、B表示出相应的事件,然后分析清楚在哪个事件发生的条件下求哪个事件的概率。
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
解:设第1次抽到理科题为事件A,第2次抽到理科题
为事件B,则第1次和第2次都抽到理科题为事件AB.
(1)从5道题中不放回地依次抽取2道的事件数为
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
解:设第1次抽到理科题为事件A,第2次抽到理科题
为事件B,则第1次和第2次都抽到理科题为事件AB.
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
(3)在第一次抽到理科题的条件下,第二次抽到理科题
的概率。
(3)解法一:由(1)(2)可得,在第一次抽到理科题
的条件下,第二次抽到理科题的概率为
例1、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
(3)在第一次抽到理科题的条件下,第二次抽到理科题
的概率。
解法二:
解法三:
(缩小样本空间)
反思
求解条件概率的一般步骤:
(1)用字母表示有关事件
(2)求P(AB),P(A)或n(AB),n(A)
( 3 )利用条件概率公式求
练习1:甲乙两地都位于长江下游,根据一百多年的气象
记录,知道甲乙两地一年中雨天所占的比例分别为20%
和18%,两地同时下雨的比例为12%,问:
(1)乙地为雨天时甲地也为雨天的概率是多少?
(2)甲地为雨天时乙地也为雨天的概率是多少?
解:设A={甲地为雨天}, B={乙地为雨天},
则P(A)=20%,P(B)=18%,P(AB)=12%,
练习1:甲乙两地都位于长江下游,根据一百多年的气象
记录,知道甲乙两地一年中雨天所占的比例分别为20%
和18%,两地同时下雨的比例为12%,问:
(3)甲乙两市至少一市下雨的概率是多少?
∵{甲乙两市至少一市下雨}=A∪B
而P(A∪B)=P(A)+P(B)-P(AB)
=20%+18%-12%
=26%
∴甲乙两市至少一市下雨的概率为26%
解:设A={甲地为雨天}, B={乙地为雨天},
则P(A)=20%,P(B)=18%,P(AB)=12%,
练一练
2.某种动物出生之后活到20岁的概率为0.7,活到25岁的概率为0.56,求现年为20岁的这种动物活到25岁的概率。
解 设A表示“活到20岁”(即≥20),B表示“活到25岁” (即≥25)
则
所求概率为
0.56
0.7
5
在某次外交谈判中,中外双方都为了自身的利益
而互不相让,这时对方有个外交官提议以抛掷一
颗骰子决定,若已知出现点数不超过3的条件下再
出现点数为奇数则按对方的决议处理,否则按中
方的决议处理,假如你在现场,你会如何抉择?
只需求事件 A 发生的条件下,
事件 B 的概率即P(B|A)
5
2
1
3
4,6
解法一(缩小样本空间法)
3.
解1:
在某次外交谈判中,中外双方都为了自身的利益
而互不相让,这时对方有个外交官提议以抛掷一
颗骰子决定,若已知出现点数不超过3的条件下再
出现点数为奇数则按对方的决议处理,否则按中
方的决议处理,假如你在现场,你会如何抉择?
只需求事件 A 发生的条件下,
事件 B 的概率即P(B|A)
5
2
1
3
4,6
3.
解2:
由条件概率定义得:
解法二(条件概率定义法)
解
4、一个盒子中有6只白球、4只黑球,从中不放回地每次任取1只,连取2次,求 (1) 第一次取得白球的概率; (2) 第一、第二次都取得白球的概率; (3) 第一次取得黑球而第二次取得白球的概率.
设A表示第一次取得白球, B表示第二次取得白球, 则
(2)
(3)
(1)
5.甲,乙,丙3人参加面试抽签,每人的试题通过不放回抽签的方式确定。假设被抽的10个试题签中有4个是难题签,按甲先,乙次,丙最后的次序抽签。试求1)甲抽到难题签,2)甲和乙都抽到难题签,3)甲没抽到难题签而乙抽到难题签,4)甲,乙,丙都抽到难题签的概率。
解 设A,B,C分别表示“甲、乙、丙抽到难签”
则
1. 条件概率的定义.
2. 条件概率的性质.
3. 条件概率的计算方法.
一、基本知识
二、思想方法
1.由特殊到一般
2.类比、归纳、推理
(1)有界性(2)可加性
(古典概型)
(一般概型)
3.数形结合
4. 求解条件概率的一般步骤
用字母表示有关事件
求相关量
代入公式求P(B|A)
课堂小结
送给同学们一段话:
在概率的世界里充满着和我们直觉截然不同的事物。面对表象同学们要坚持实事求是的态度、锲而不舍的精神。尽管我们的学习生活充满艰辛,但我相信只要同学们不断进取、挑战自我,我们一定会达到成功的彼岸!
